- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Конференция по истории математики Арабская математика
Содержание
- 1. Конференция по истории математики Арабская математика
- 2. Слайд 2
- 3. При изучении истории любой науки можно проследить
- 4. Андрей Николаевич Колмогоров (1903-1987), русский математик. В
- 5. I период
- 6. Предпосылки развития и особенности математики в странах ислама средневекового периода
- 7. В 146 году до н. э. Рим захватывает Грецию,
- 8. Арабский халифат 750г. В VII в.
- 9. Доступная нам история математики в странах Ближнего
- 10. Ряд интересных математических задач, стимулировавших развитие сферической
- 11. Значительное место занимали задачи, возникавшие при строительстве
- 12. В начале IX века научным центром халифата
- 13. НумерацияУчёные мусульманского средневековья пользовались двумя основными видами
- 14. Абу́ Абдулла́х Муха́ммад ибн Муса́ аль-Хорезми́ (араб.
- 15. Муххамад ибн Муса аль-Хорезми, уроженец Хорезма, был
- 16. Свой замечательный трактат по алгебре ал-Хорезми написал
- 17. Один персидский математик методы «ал-джебр» и «вал-мукабала»
- 18. Содержание трактата в основном сводится к решению
- 19. Что касается арифметического трактата ал-Хорезми, то он
- 20. Математический труд аль-Хорезми еще в XII веке
- 21. Аль-Бируни X-XIвв
- 22. БИРУНИ (Абу-р-Райхан Мухаммад ибн Ахмад ал-Бируни) –
- 23. Основные работы (свыше 40) посвящены математике и
- 24. Будучи ученым-естествоиспытателем, Бируни, внес вклад в расширение
- 25. О необыкновенных способностях ученого-энциклопедиста и астролога ходили
- 26. Омар Хайям XI-XIIввГиясадди́н Абу-ль-Фатх Ома́р ибн Ибрахим аль-Хайя́м Нишапури́-персидский поэт, философ, математик, астроном, астролог.
- 27. Детство Уроженец города Нишапура в Хорасане (ныне иранская провинция Хорасан-Резави). Омар был сыном палаточника,
- 28. Математика Хайяму принадлежит «Трактат о доказательствах задач
- 29. В 1077 г. Хайям закончил работу над важным
- 30. Асторономия Хайям возглавлял группу астрономов Исфахана, которая в
- 31. РубаиПри жизни Хайям был известен исключительно как
- 32. Слайд 32
- 33. Аль-КашиXIV-XVвв
- 34. Гияс-ад-дин Джамшид ибн Масуд аль-Каши (перс. غیاثالدین
- 35. В трактате «Ключ арифметики» Аль-Каши описывает шестидесятеричную
- 36. При записи десятичных дробей Аль-Каши отделяет целую
- 37. В «Трактате об окружности» Аль-Каши вычисляет длину
- 38. Число сторон рассматриваемого им многоугольника Аль-Каши подбирает
- 39. =3,141590265358979325 Из 17 десятичных знаков π
- 40. Математики стран ислама получили первый толчок к
- 41. Математика Востока, в отличие от древнегреческой математики,
- 42. Задача.Определить длину рыбы в пядях, если одна
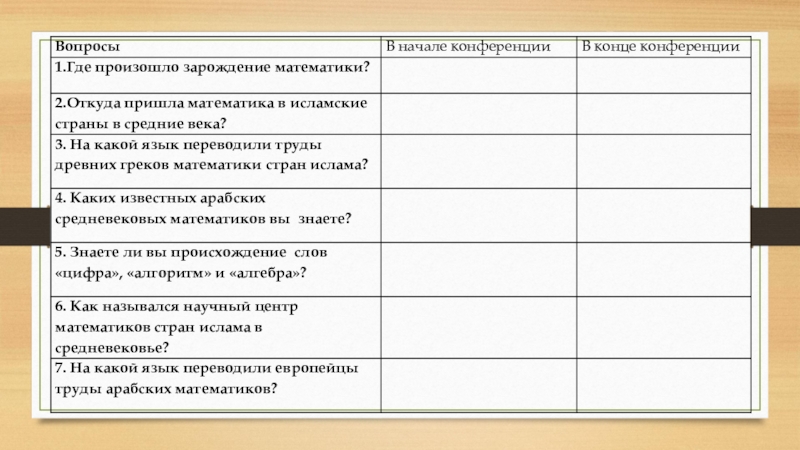
- 43. Предлагается вторично ответить на вопросы теста.1.Где произошло зарождение математики?
- 44. В Древнем Египте и Древнем Вавилоне.
- 45. 2.Откуда пришла математика в исламские страны в средние века?
- 46. В страны ислама математика пришла из Древней Греции и Индии.
- 47. 3. На какой язык переводили труды древних греков математики стран ислама?
- 48. На арабский.
- 49. 4. Каких известных арабских средневековых математиков вы знаете?
- 50. Аль-Хорезми, Аль-Бируни, Омар Хайям, Аль-Каши, Ибн-Сина (Авиценна), Улугбек …
- 51. 5. Знаете ли вы происхождение слов «цифра»,«алгоритм» и «алгебра»?
- 52. Нуль индийцы называли «сунья» – «пустое»,
- 53. 6. Как назывался научный центр математиков стран ислама в средневековье?
- 54. Дом мудрости в Багдаде.
- 55. 7. На какой язык переводили европейцы труды арабских математиков?
- 56. На латинский. Dixi Algoritmi…
Слайд 3При изучении истории любой науки можно
проследить развитие (генезис) идей, как
возникали и в какие формы их облекали учёные. Каждому учёному приходится, занимаясь какой-либо наукой, изучать её историю, чтобы понять какое место в этой науке занимают его исследования и открытия, а также чтобы «заново не изобретать велосипед». Кроме того, при неожиданных открытиях в истории науки удаётся удлинить её прошлое и память человечества.
Слайд 4Андрей Николаевич Колмогоров (1903-1987), русский математик.
В периодизации истории математики, которую дал
1) период зарождения математики до VI-V века до н.э.
2) математика постоянных величин до XVII века н.э. (внутри этого периода отдельно выделяется арабская математика с IX по XV в.н.э.)
3)математика переменных величин с XVII –до середины XIX в.н.э.
4) современная математика с середины XIX в.н.э.
Слайд 5I период
! (наука основана на доказательстве – ! матем. переем величин! совр. матем
! дедуктивная математика) ! !
Зарождение математики! Математика пост. величин ! !
__________________VI-Vв. до н.э. ______0________________XVI-XVII в____________2 полов________
XIXв
Слайд 7В 146 году до н. э. Рим захватывает Грецию, а в 31 году
Приход христианства и частые смуты в империи резко снизили интерес к науке. Отдельные учёные труды ещё появляются в Афинах, но в 529 году Юстиниан закрыл Афинскую академию как рассадник язычества.
Часть учёных переехала в Персию или Сирию и
продолжала труды там. От них уцелевшие сокровища
античного знания получили учёные стран ислама.
Дальнейшее развитие математики было связано с
арабоязычным Востоком. Учёные Сирии, Египта,
Хорезма, Ирана и других стран, покорённых арабами,
писали научные трактаты на арабском языке.
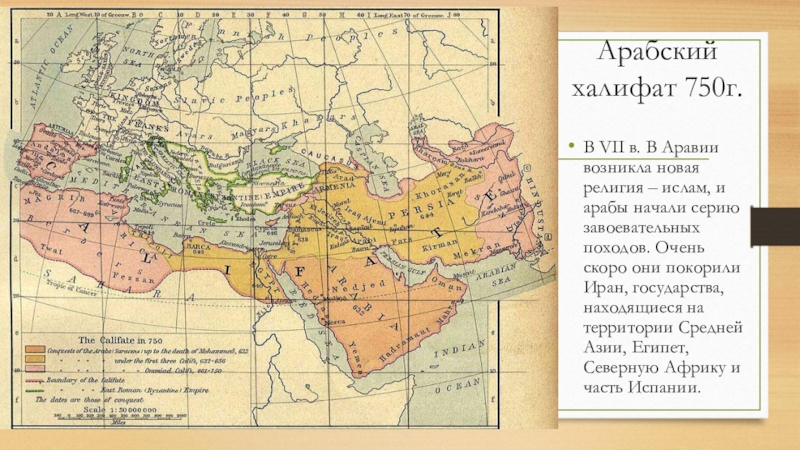
Слайд 8Арабский
халифат 750г.
В VII в. В Аравии возникла новая религия –
Слайд 9Доступная нам история математики в странах Ближнего и Среднего Востока начинается
Слайд 10Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, поставила
определении точного времени для
совершения намаза (канонической молитвы),
а также об определении
киблы — точного направления на Мекку.
Мечеть аль-Харам и Мекка в XX в
Слайд 11Значительное место занимали задачи, возникавшие при строительстве каналов и плотин, дорог,
Естественно поэтому, что самых значительных успехов средневековые восточные учёные достигли именно в области вычислительной математики. В тоже время получили развитие и теоретические разделы таких математических дисциплин, как алгебра, геометрия, тригонометрия.
Слайд 12В начале IX века научным центром халифата становится Багдад, где халифы
Слайд 13Нумерация
Учёные мусульманского средневековья пользовались двумя основными видами нумерации заимствованными у индийцев
Индийские цифры в странах арабского и Среднего Востока отличались от цифр в странах арабского Запада (посление назывались «губар» – «пыль», т.к. изначально использовались на счётной доске покрытой пылью). Наши цифры произошли от цифр губар.
Индийская система нумерации приобрела широкую известность в странах Ближнего и Среднего Востока благодаря арифметическому трактату Муххамада ал-Хорезми.
Слайд 14Абу́ Абдулла́х Муха́ммад ибн Муса́ аль-Хорезми́ (араб. أبو عبد الله محمد
Слайд 15Муххамад ибн Муса аль-Хорезми, уроженец Хорезма, был первым крупным учёным-энциклопедистом, работавшим
Совместно с другими учёными он по приказу халифа в пустыне Санджар проводил специальные измерения длины градуса дуги земного меридиана с целью определения размеров земного шара. Эти измерения на протяжении 700 лет оставались не превзойденными по точности. При активном участии аль-Хорезми была составлена знаменитая карта ал-Маъмуна. Эта географическая карта, дошедшая до наших дней, содержала ценные сведения о материках и морях, обитаемых землях и пустынях, горах, реках и их истоках, о городах и селениях. В ней были также астрономические сведения.
Научное наследие аль-Хорезми составляло почти двадцать книг, из которых сохранилось не более десяти. Наибольшей известностью пользуется его "Китаб ал-джабр вал-мукабала" (Книга восстановления и противопоставления) и "Зидж" (Астрономические таблицы). Многие поколения ученых как на Востоке, так и на Западе пользовались таблицами аль-Хорезми. Особенно велика значимость его книги "Ал-джабр вал-мукабала", которая дала название такому разделу математики, как алгебра (ал-джабр). Аль-Хорезми писал, что его математический труд найдет практическое приложение, "когда необходимо измерение земли, рытье каналов и для всяких других вещей".
Слайд 16Свой замечательный трактат по алгебре ал-Хорезми написал также по указанию ал-Мамуны
Сочинение преимущественно посвящается решению уравнений первой и второй степени. Для решения подобных уравнений он предложил метод «восстановления» (ал-джебр) и «сопоставления» (вал-му-кабала).
Первая страница книги Китаб аль-джебр ва-ль-мукабала
Слайд 17Один персидский математик методы «ал-джебр» и «вал-мукабала» даже изложил стихами.
Ал-джебр
При решении
Вал-мукабала
Дальше смотрим в уравненье,
Можно ль сделать приведенье,
Если члены есть подобны,
Сопоставить их удобно.
Вычитая равный член из них,
К одному приводим их.
Памятник аль-Хорезми в г. Ургенче
Слайд 18Содержание трактата в основном сводится к решению числовых квадратных уравнений, которые
Слайд 19Что касается арифметического трактата ал-Хорезми, то он явился источником распространения в
Алгебраический и арифметический трактаты хорезмского ученого, конечно, трудно переоценить, ибо оба они сыграли огромную роль в истории не только математики, но и всей человеческой культуры.
В заключение надо отметить, что термин «алгебра», как международное название математической науки, произошел от слова «ал-джебр», т. е. от названия трактата ал-Хорезми «Китаб ал-джебр вал-мукабала». Интересно отметить также, что термин «алгоритм» (общее решение любой математической задачи) есть не что иное, как искаженное имя «ал-Хорезми».
Слайд 20Математический труд аль-Хорезми еще в XII веке был переведен с арабского
Слайд 22БИРУНИ (Абу-р-Райхан Мухаммад ибн Ахмад ал-Бируни) – среднеазиатский ученый-энциклопедист. Родился он
Мамуна, возглавлял Академию, которая объединяла виднейших ученых, в том
числе Абуали ибн-Сино (Авиценна), Мухаммад ибн-Муса (ал-Хорезми). Уже в детские годы Бируни отличался поразительной трудоспособностью,
умением погружаться в работу с головой, полностью отрешаться от
повседневных будничных забот. Учитель Абу Наср начал приобщать его к математике, едва мальчик научился писать. Впрочем, не исключено, что первые шаги Бируни были сделаны еще до этого. Ведь «арифметике пыли», требующей умения выводить цифры на покрытой песком счетной доске, предшествовали две другие: «арифметика воздуха», в которой все вычисления производятся в уме, и «арифметика пальцев», где твои счетные инструменты всегда находятся при тебе. Научные труды Бируни охватывают различные области знаний: астрономию и географию, математику и физику, геологию и минералогию, химию и ботанику, историю и этнографию, философию и филологию.
Слайд 23Основные работы (свыше 40) посвящены математике и астрономии, которая имела
огромное
земледелия и торговых путешествий.
Важнейшей задачей астрономии было совершенствование календаря и методов
ориентирования на Земле по небесным светилам. Необходимо было уметь как можно
точнее определять положения на небе Солнца, Луны, звезд, а также измерять,
с наиболее возможной точностью, так называемые, основные астрономические постоянные: наклон эклиптики к экватору, длину солнечного и звездного года и др. Это, в свою очередь, требовало развития математики, в частности, плоской и сферической тригонометрии – с одной стороны, и совершенствования инструментов для точных наблюдений – с другой. Результаты и достижения Бируни во всех перечисленных областях оставались непревзойденными в течение нескольких веков. Он придумал самый крупный стенной квадрант: угломерный инструмент, позволявший измерять положение Солнца с точностью до 2'. Дал самое точное определение наклона эклиптики к экватору и векового изменения этой величины. Изобрел новый метод определения радиуса Земли – по степени понижения горизонта при наблюдении с горы. Бируни почти точно определил радиус Земли (более 6000 км), исходя из представления о ее шарообразной форме.
Слайд 24Будучи ученым-естествоиспытателем, Бируни, внес вклад в
расширение понятия числа, теорию кубических
сферическую тригонометрию, составил тригонометрические
таблицы. Тригонометрии посвящена III книга «Канона Мас’уда»
ал-Бируни, где имеется весьма точная таблица синусов и тангенсов, в
Основе вычисления которой лежит приближённое решение
ал-Бируни задачи трисекции угла. Помимо своего родного хорезмийского языка, ал-Бируни владел
арабским, персидским, греческим, латинским, турецким,
сирийским языками, а также ивритом, санскритом и хинди. Умирал в полном сознании и, попрощавшись со всеми друзьями, спросил последнего: «Что ты толковал мне однажды о методах счёта неправедных прибылей?» «Как Вы можете думать об этом в таком состоянии?» — изумленно воcкликнул тот. «Эх ты! — сказал Бируни еле слышно. — Я думаю, что покинуть сей мир, зная ответ на этот вопрос, лучше, чем уйти из него невеждой
Перечень работ, составленный его учениками, составил 60 страниц мелким шрифтом. Писал на арабском языке[
Слайд 25О необыкновенных способностях ученого-энциклопедиста и астролога ходили легенды еще при его
Слайд 26Омар Хайям
XI-XIIвв
Гиясадди́н Абу-ль-Фатх Ома́р ибн Ибрахим аль-Хайя́м Нишапури́-персидский поэт, философ, математик, астроном, астролог.
Слайд 27Детство
Уроженец города Нишапура в Хорасане (ныне иранская провинция Хорасан-Резави). Омар был сыном палаточника, также у него была
Детство Хайяма пришлось на жестокий период сельджукского завоевания Центральной Азии.Как и другие крупные учёные того времени, Омар не задерживался подолгу в каком-то городе. Всего через четыре года он покинул Самарканд и переехал в Бухару, где начал работать в хранилищах книг. За десять лет, что учёный прожил в Бухаре, он написал четыре фундаментальных трактата по математике.
Слайд 28Математика
Хайяму принадлежит «Трактат о доказательствах задач алгебры и алмукабалы», в
Слайд 29В 1077 г. Хайям закончил работу над важным математическим трудом — «Комментарии к
Слайд 30Асторономия
Хайям возглавлял группу астрономов Исфахана, которая в правление сельджукского султана Джалал ад-Дина Малик-шаха
разработала принципиально новый
принят официально в 1079 г. Основным предназначением этого календаря была как можно более строгая привязка Новруза (то есть начала года) к весеннему равноденствию, понимаемому как вхождение солнца в зодиакальное созвездие Овна. Для отличия от зороастрийского солнечного года, называвшегося «древним» или «персидским» , новый календарь стали называть по имени султана — «Джалали» или «Малеки». Количество дней в месяцах календаря «Джалали» варьировало в зависимости от сроков вступления солнца в тот или иной зодиакальный знак и могло колебаться от 29 до 32 дней. Месяцы стали именоваться в общем случае именем соответствующего знака зодиака.
Слайд 31Рубаи
При жизни Хайям был известен исключительно как выдающийся учёный. На протяжении
Много лет размышлял я над жизнью земной. Непонятного нет для меня под луной. Мне известно, что мне ничего не известно, - Вот последний секрет из постигнутых мной.
Известно, в мире все лишь суета сует: Будь весел, не горюй, стоит на этом свет. Что было, то прошло, что будет - неизвестно, Так не тужи о том, чего сегодня нет.
Слайд 34Гияс-ад-дин Джамшид ибн Масуд аль-Каши (перс. غیاثالدین جمشید کاشانی,1380, Кашан (Иран)
Слайд 35В трактате «Ключ арифметики» Аль-Каши описывает шестидесятеричную систему счисления. (В астрономических
Слайд 36При записи десятичных дробей Аль-Каши отделяет целую часть от дробной вертикальной
Разряды десятичных дробей он называет десятичными минутами, десятичными секундами, десятичными терциями и т.д.
Слайд 37В «Трактате об окружности» Аль-Каши вычисляет длину окружности по рецепту Архимеда
Слайд 38Число сторон рассматриваемого им многоугольника Аль-Каши подбирает таким образом, чтобы разность
Слайд 39
=3,141590265358979325
Из 17 десятичных знаков π после запятой, здесь неверен только
Этим он поставил рекорд, продержавшийся до 1596 г., когда Людольф ван Цейлен вычислил число π с 35 десятичными знаками. Кроме того, наверняка можно сказать, что эта работа Аль-Каши была первым исторически зафиксированным примером переведения дроби из одной системы счисления в другую.
Слайд 40Математики стран ислама получили первый толчок к занятиям кубическими уравнениями от
Слайд 41Математика Востока, в отличие от древнегреческой математики, всегда носила более практичный
Слайд 42
Задача.
Определить длину рыбы в пядях, если одна третья часть ее длины
Бег Эддин