- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Комплексные числа (10-11 классы)
Содержание
- 1. Комплексные числа (10-11 классы)
- 2. ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ ЧИСЛОВЫЕ
- 3. Понятие комплексного числаХ+А=В - недостаточно положительных
- 4. Слайд 4
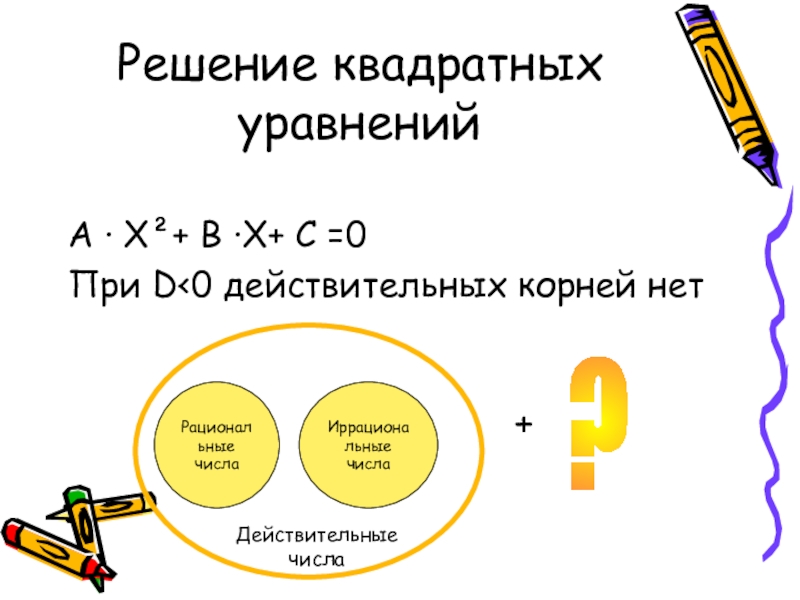
- 5. Решение квадратных уравненийА · Х²+ В ·Х+ С =0При D
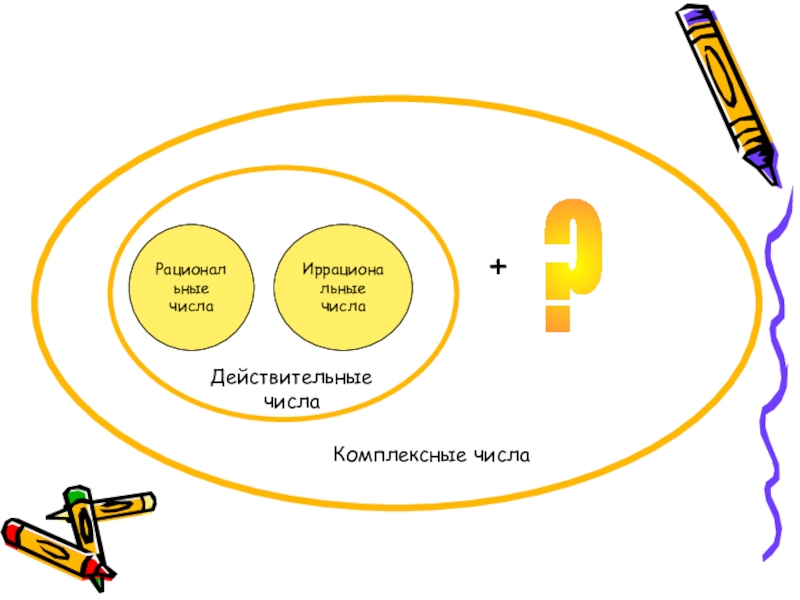
- 6. Комплексные числа
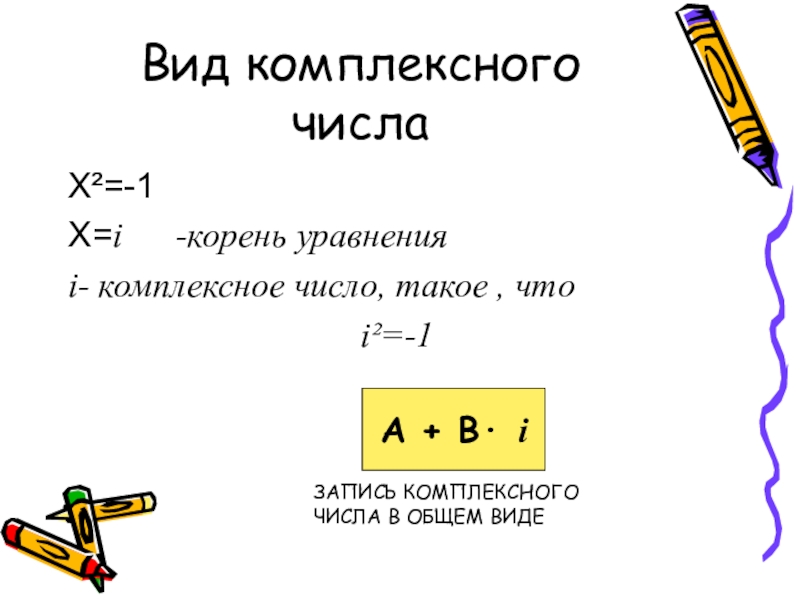
- 7. Вид комплексного числаХ²=-1Х=i -корень уравненияi-
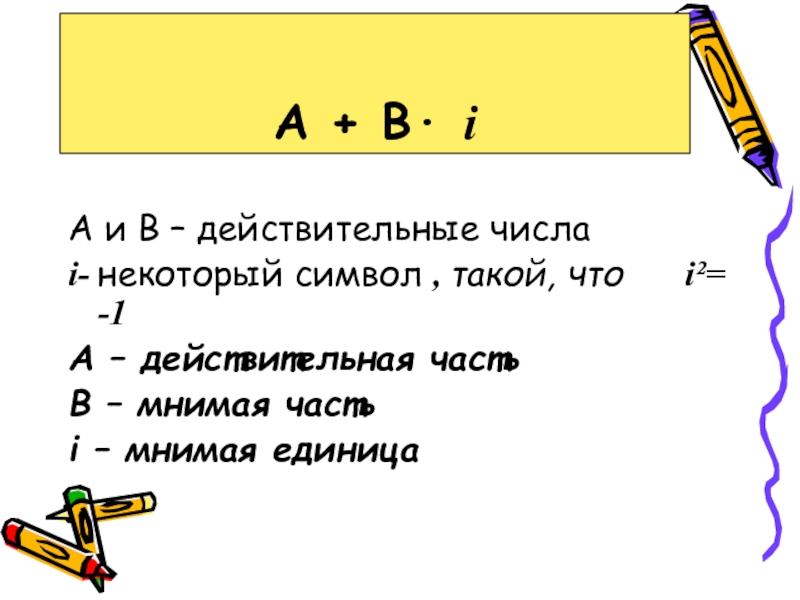
- 8. А и В – действительные числаi- некоторый
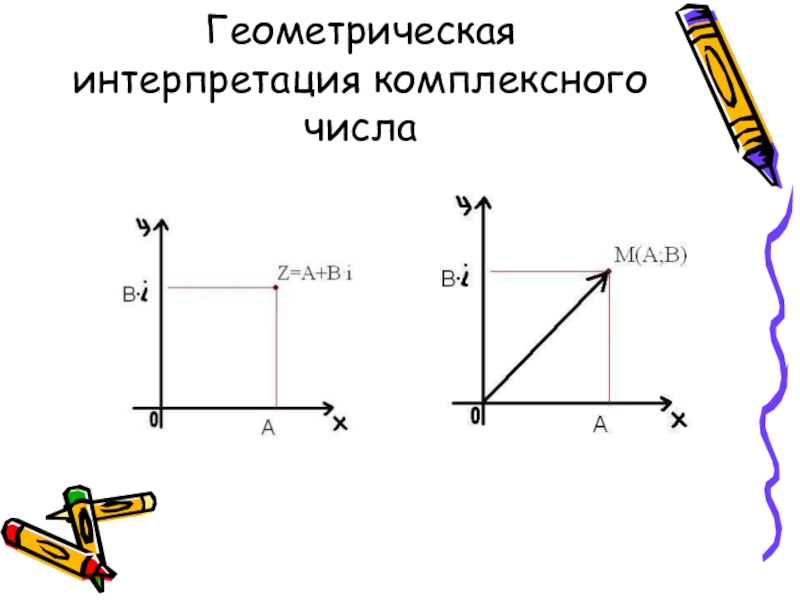
- 9. Геометрическая интерпретация комплексного числа
- 10. Модуль комплексного числаZ=А - В· iСОПРЯЖЕННОЕZ= А
- 11. Тригонометрическая форма комплексного числа Z =rφ- аргумент
- 12. Т.к Z =r =Z= А
- 13. Сложение и умножение комплексных чиселАлгебраическая формаГеометрическая формаСумма(A+iB)
- 14. Если Z 1= Z2, то получимZ²=[r (cos
- 15. Число Z называется корнем степени n
- 16. Вторая формула Муавра определяет все корни двучленного
- 17. Пример:Решить уравнение:
- 18. Свойства сложения и умноженияПереместительное свойство:Сочетательное свойство:Распределительные свойство:Z1
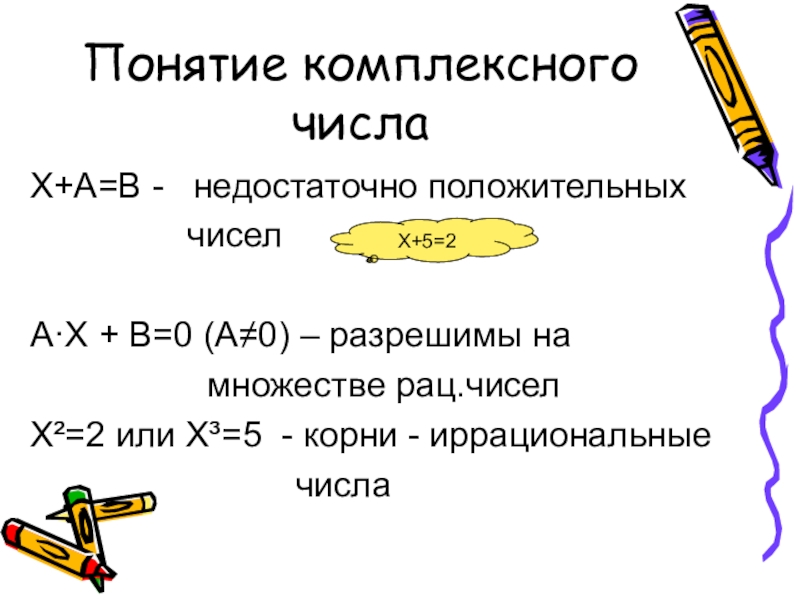
- 19. Геометрическое изображение суммы комплексных чисел
- 20. Вычитание и деление комплексных чиселZ+ Z2 =
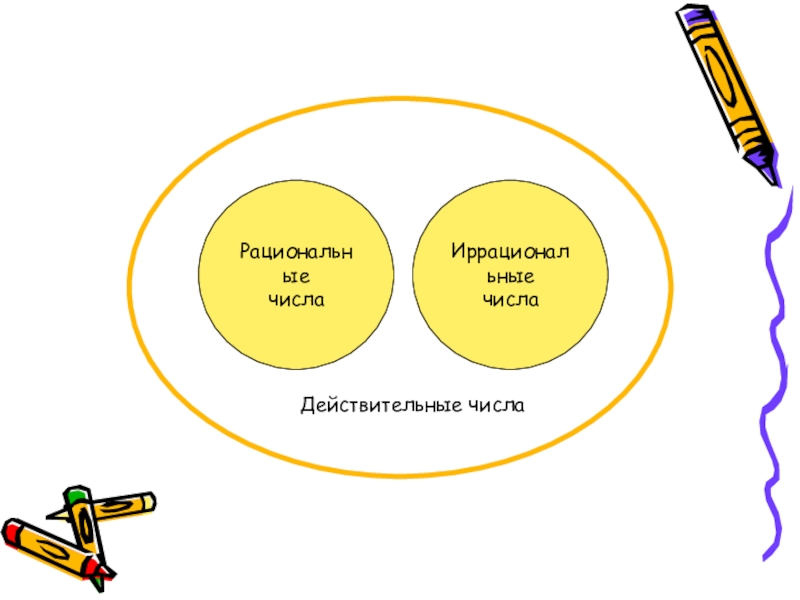
- 21. Геометрическое изображение разности комплексных чисел
- 22. Примеры:Найти разность и частное комплексных чиселРешение:
- 23. Литература Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В.
Слайд 2ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ
ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ
ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Комплексные
Слайд 3Понятие комплексного числа
Х+А=В - недостаточно положительных
А·Х + В=0 (А≠0) – разрешимы на
множестве рац.чисел
Х²=2 или Х³=5 - корни - иррациональные
числа
Х+5=2
Слайд 7Вид комплексного числа
Х²=-1
Х=i -корень уравнения
i- комплексное число, такое ,
i²=-1
А + В· i
ЗАПИСЬ КОМПЛЕКСНОГО ЧИСЛА В ОБЩЕМ ВИДЕ
Слайд 8
А и В – действительные числа
i- некоторый символ , такой, что
А – действительная часть
В – мнимая часть
i – мнимая единица
А + В· i
Слайд 10Модуль комплексного числа
Z=А - В· i
СОПРЯЖЕННОЕ
Z= А + В· i
(Z) =
Комплексно сопряженные числа.
Z = A + B i=
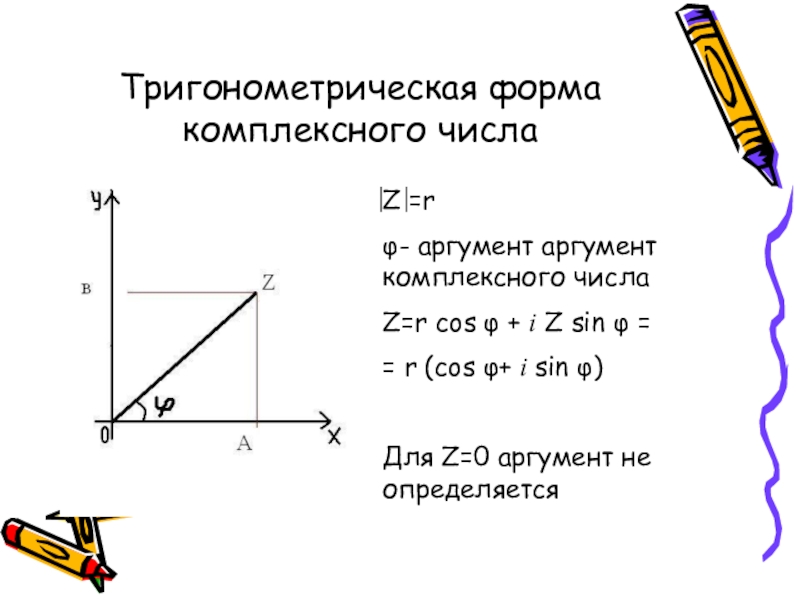
Слайд 11Тригонометрическая форма комплексного числа
Z =r
φ- аргумент аргумент комплексного числа
Z=r cos
= r (cos φ+ i sin φ)
Для Z=0 аргумент не определяется
Слайд 13Сложение и умножение комплексных чисел
Алгебраическая форма
Геометрическая форма
Сумма
(A+iB) + (C+iD)=
(A+C)+(B+D)I
Произведение
Z1=
Z2= r2(cos φ2+ i sin φ2)
Z1 ·Z2= r1r2[cos( φ1+ φ2)+isin ( φ1+ φ2)]
Произведение
(A+iB) · (C+iD)=
(AC-BD)+(AD+BC)i
Слайд 14Если Z 1= Z2, то получим
Z²=[r (cos φ+ i sin φ)]²=
Z³= Z²·Z=[r (cos φ+ i sin φ)]²·r (cos φ+
i sin φ)= r³ (cos3 φ+ i sin 3φ)
Формула Муавра
Для любого Z= r (cos φ+ i sin φ)≠0 и любого натурального числа n
Слайд 15
Число Z называется корнем степени n из числа ω (обозначается
Из данного определения вытекает, что каждое решение уравнения
является корнем степени n из числа ω.
Z= r (cos φ+ i sin φ)
ω= ρ(cos ψ+ i sin ψ)
Вторая формула Муавра
Слайд 16Вторая формула Муавра определяет все корни двучленного уравнения степени n
Каждое алгебраическое
Теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайне мере один корень
Слайд 18Свойства сложения и умножения
Переместительное свойство:
Сочетательное свойство:
Распределительные свойство:
Z1 + Z2 = Z1
Z1 · Z2 = Z1 ·Z2
Z1 ·(Z2 + Z3 )= Z1 · Z2+ Z1 · Z3
(Z1 + Z2 )+Z3 = Z1 +(Z2+Z3)
(Z1 · Z2 ) · Z3 = Z1 ·(Z2 · Z3)
Слайд 20Вычитание и деление комплексных чисел
Z+ Z2 = Z1
Вычитание – операция,
Z+ Z2 +(- Z2 )= Z1 +(- Z2 )
Z= Z1 - Z2 –разность
Деление – операция, обратная умножению:
Z · Z2 = Z1
Разделив обе части на Z2 получим:
Слайд 23Литература
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др/ Алгебра и
Колмагоров А.Н., Абрамов, Дудицин/ Алгебра и начала анализа 10-11кл, Просвещение 2005г
НикольскийС.М., Потапов Н.К, и др. Алгебра и начала анализа 10-11кл, Просвещение 2005г



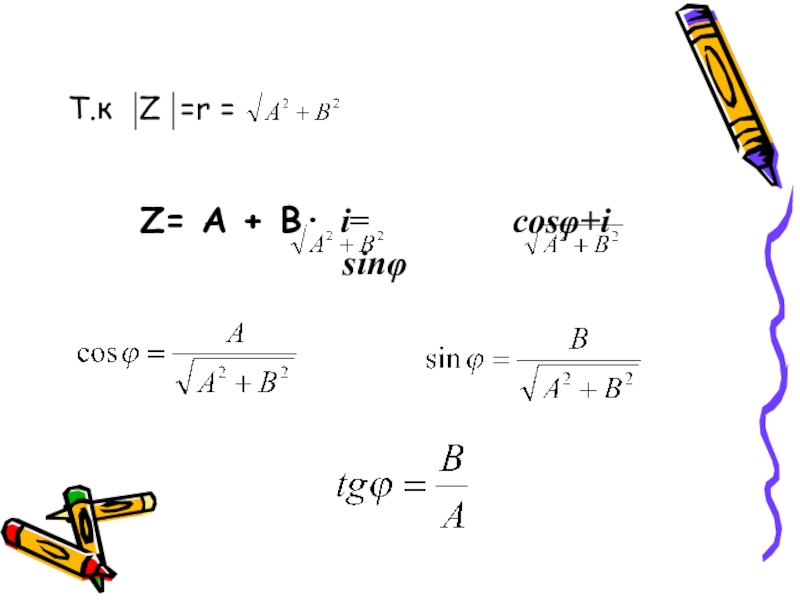

![Комплексные числа (10-11 классы) Если Z 1= Z2, то получимZ²=[r (cos φ+ i sin φ)]²= Если Z 1= Z2, то получимZ²=[r (cos φ+ i sin φ)]²= r² (cos2 φ+ i](/img/thumbs/b6d86e275cba03cda2adec8de696ef34-800x.jpg)