- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследование функции при помощи производной
Содержание
- 1. Исследование функции при помощи производной
- 2. 4.Отмечаем эти точки на числовой прямойи определяем
- 3. Исследование по формулепо графику
- 4. Если f/(x) > 0, значит, функция возрастает. Если f/(x) < 0, значит, функция убывает. Признаки:
- 5. По формуле функции
- 6. Найдите промежутки возрастания (убывания) функции. Задания:Практикум:
- 7. Слайд 7
- 8. -11+-1++---
- 9. Графики.Графики функцийГрафикипроизводных
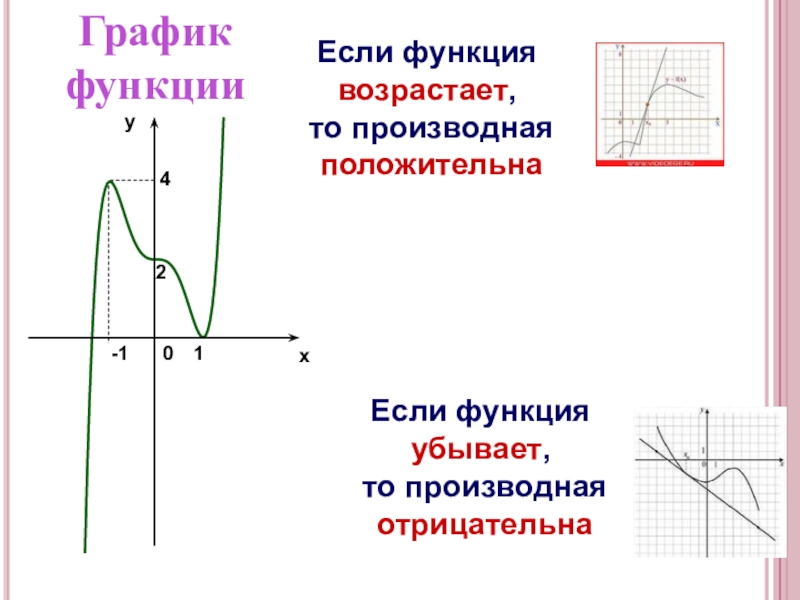
- 10. xy2-1140Если функция возрастает, то производная положительнаЕсли функция убывает, то производная отрицательнаГрафикфункции
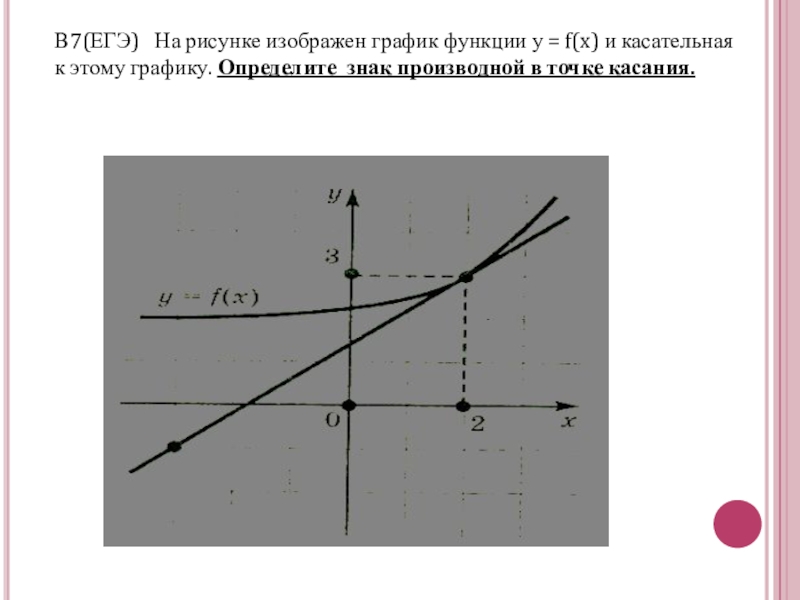
- 11. В7(ЕГЭ) На рисунке изображен график функции
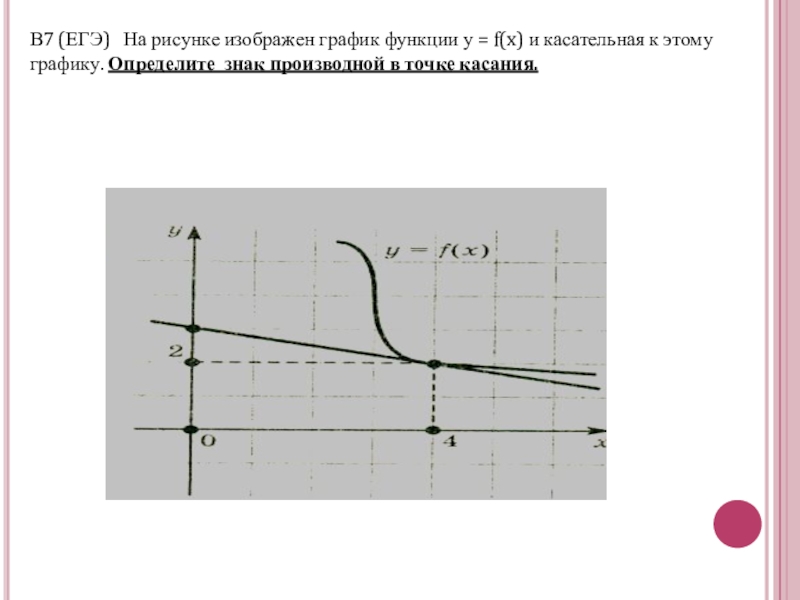
- 12. В7 (ЕГЭ) На рисунке изображен график
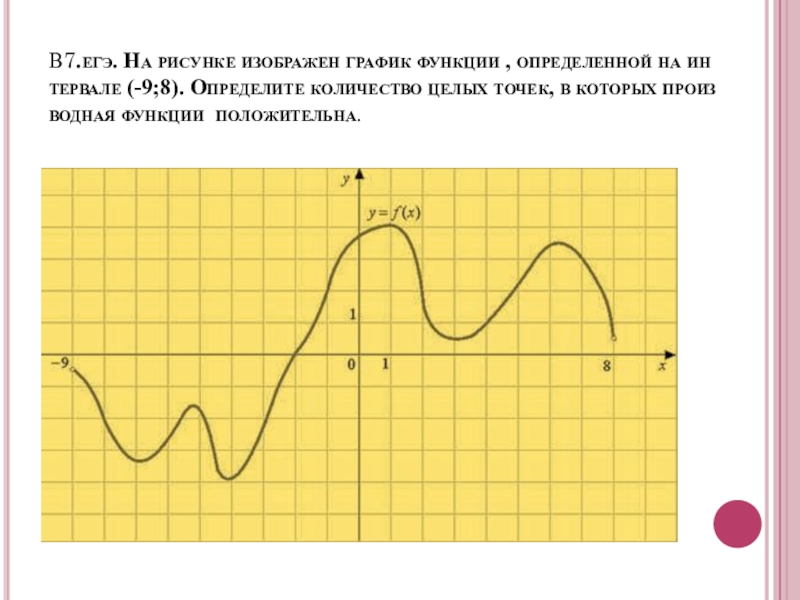
- 13. В7.егэ. На рисунке изображен график функции , определенной на интервале (-9;8). Определите количество целых точек, в которых производная функции положительна.
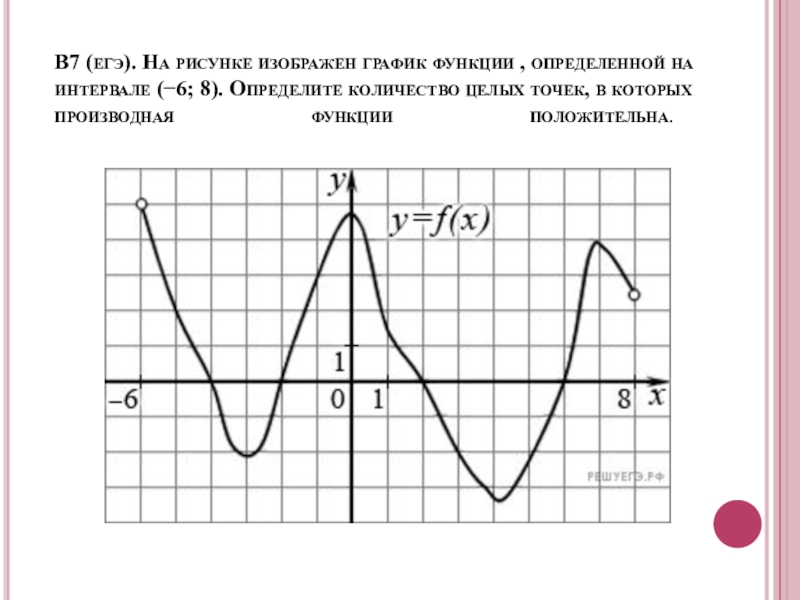
- 14. В7 (егэ). На рисунке изображен график функции , определенной
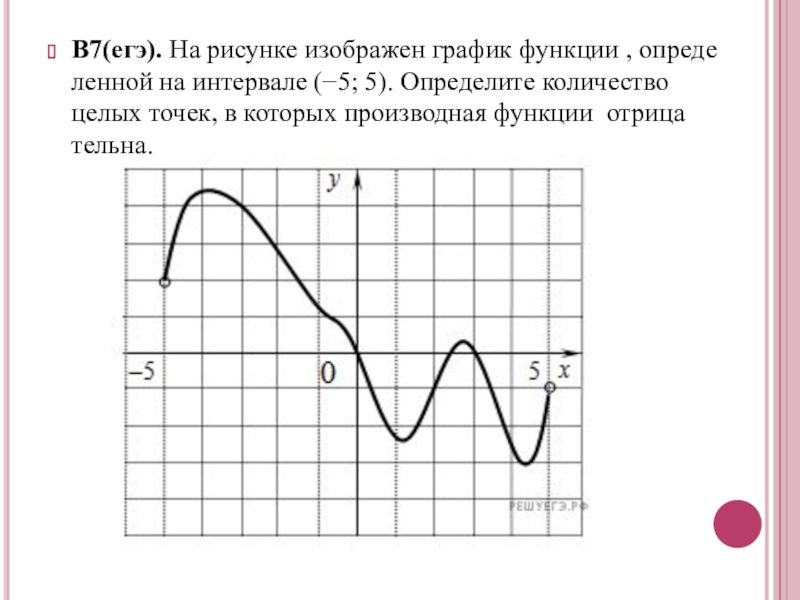
- 15. В7(егэ). На рисунке изображен график функции , определенной на интервале
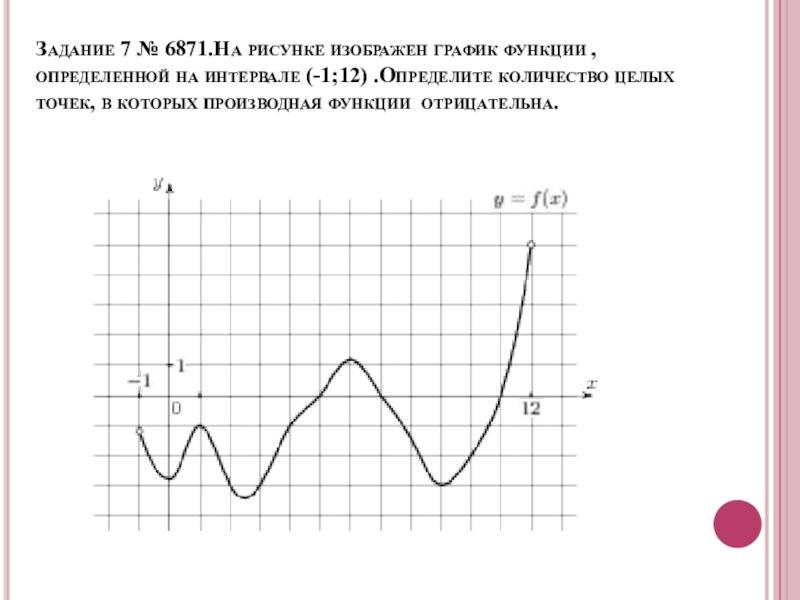
- 16. Задание 7 № 6871.На рисунке изображен график функции , определенной
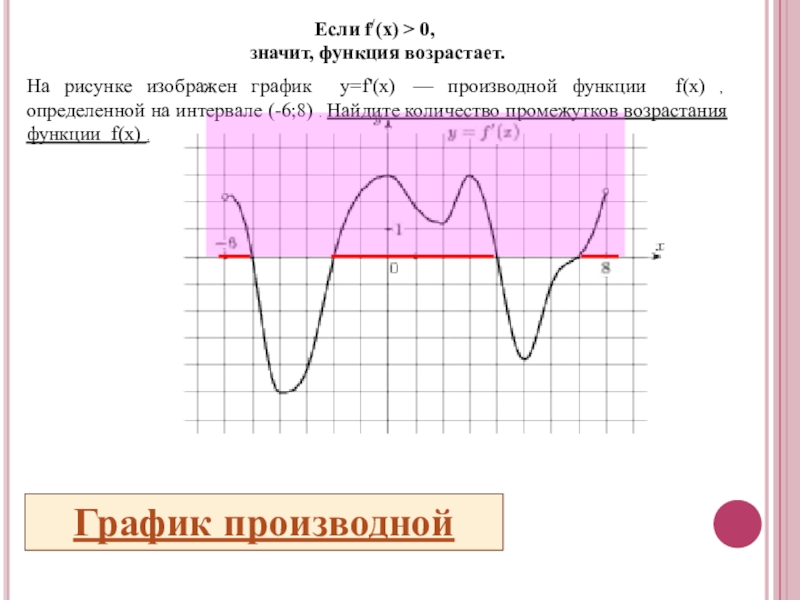
- 17. Если f/(x) > 0, значит, функция возрастает.
- 18. На рисунке изображен график y=f'(x) — производной
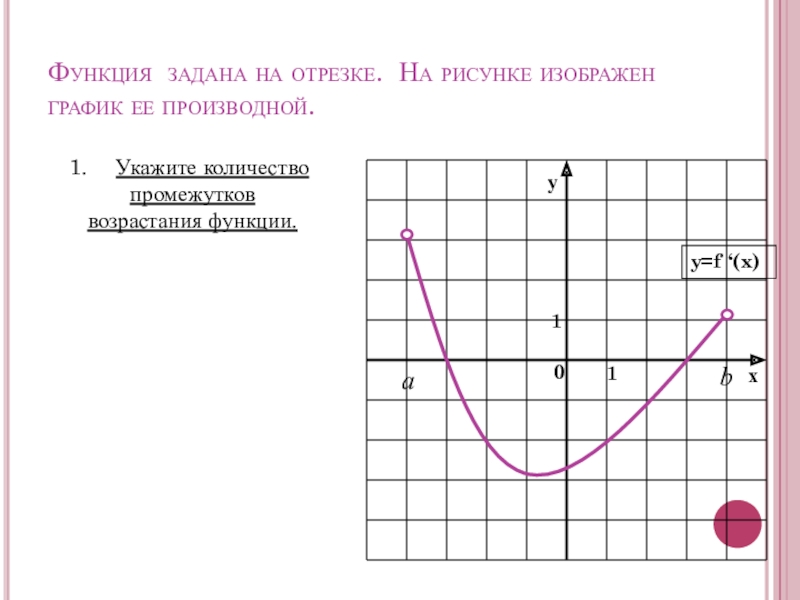
- 19. Функция задана на отрезке. На рисунке изображен график ее производной.Укажите количество промежутков возрастания функции.bа
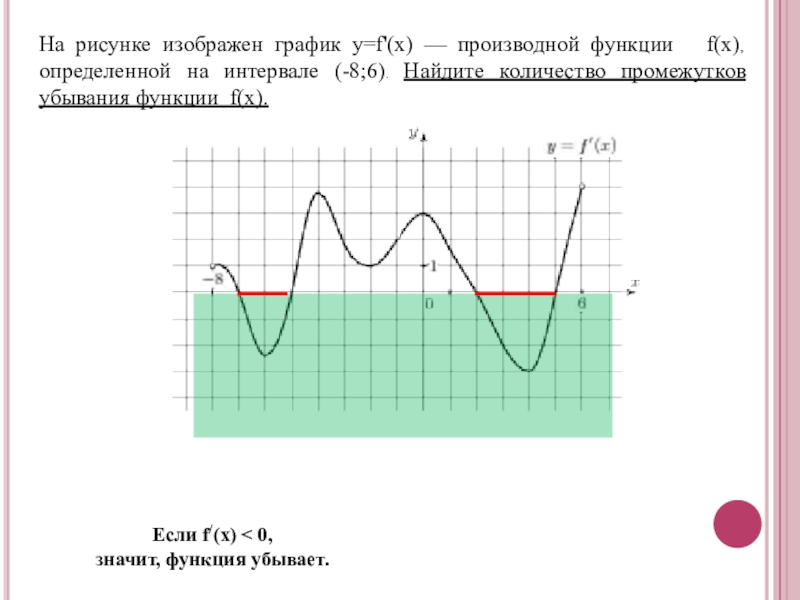
- 20. На рисунке изображен график y=f'(x) — производной
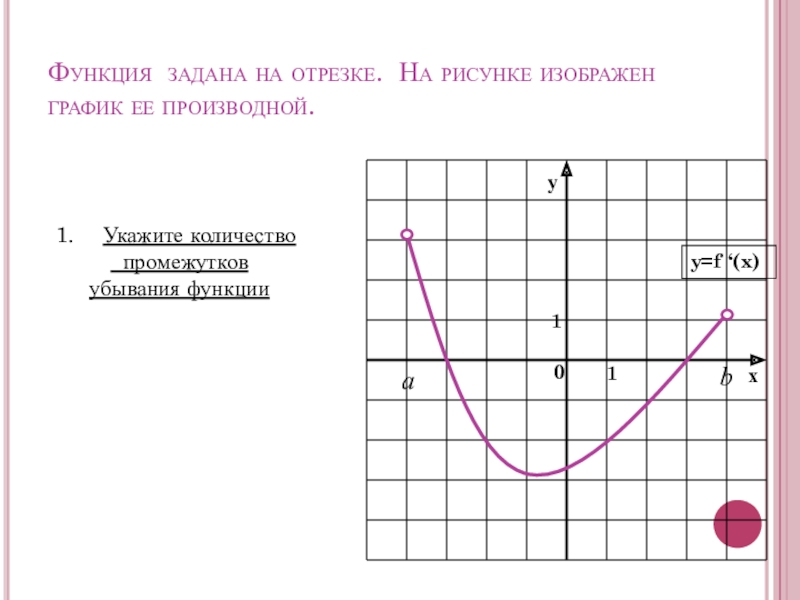
- 21. Функция задана на отрезке. На рисунке изображен график ее производной.Укажите количество промежутковубывания функцииbа
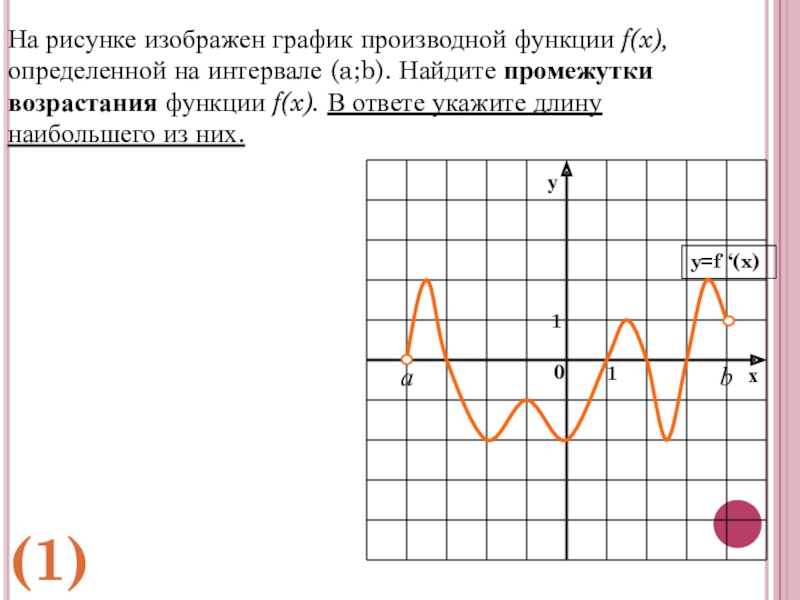
- 22. bаНа рисунке изображен график производной функции f(x),определенной
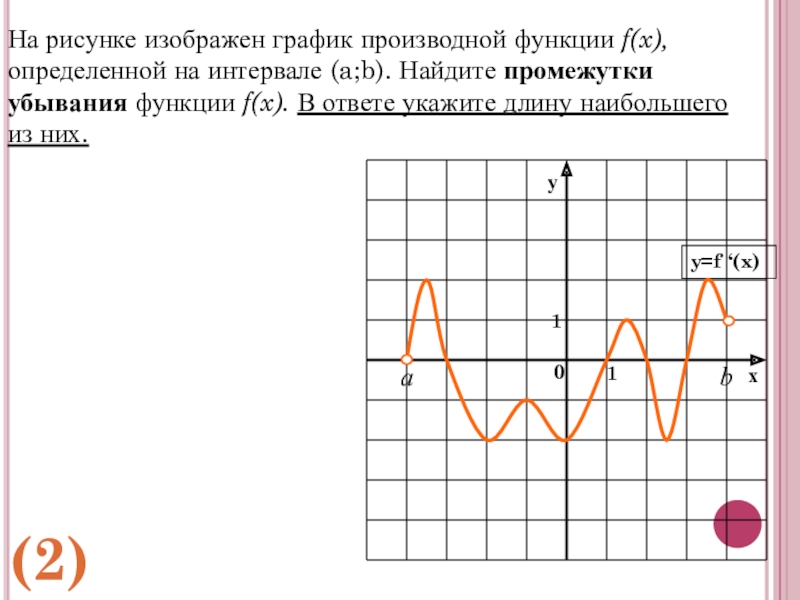
- 23. bаНа рисунке изображен график производной функции f(x),определенной
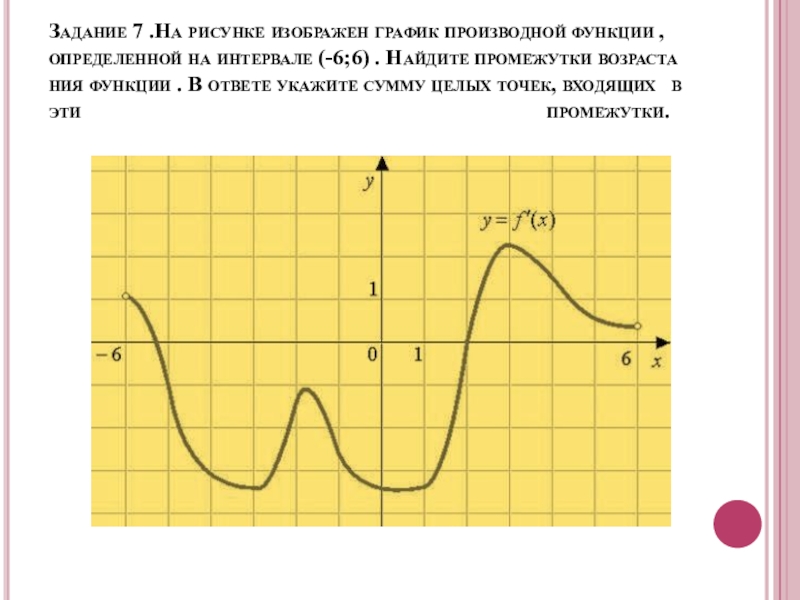
- 24. Задание 7 .На рисунке изображен график производной функции , определенной
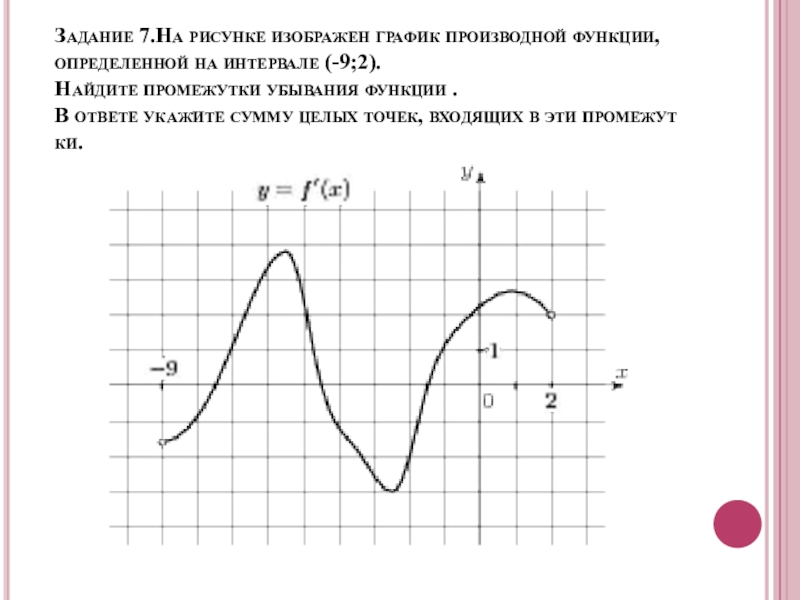
- 25. Задание 7 .На рисунке изображен график производной функции , определенной
- 26. Задание 7.На рисунке изображен график производной функции,
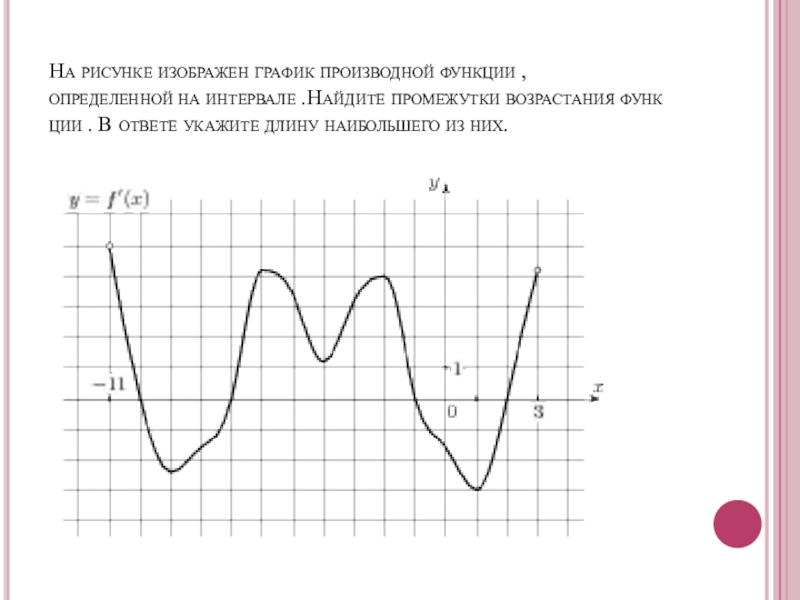
- 27. На рисунке изображен график производной функции , определенной
- 28. Домашнее задание:Составить подборку однотипных заданий В7 из сборника егэ, прорешать.
- 29. Спасибо за урок!
Слайд 24.Отмечаем эти точки на числовой прямой
и определяем знаки производной
на полученных
3.Находим точки, в которых f’(x) =0
или f’(x) не существует
Алгоритм нахождения промежутков возрастания (убывания) функции
1. Находим область определения функции
2.Находим производную функции
5.Делаем выводы о промежутках
возрастания и убывания
Слайд 10x
y
2
-1
1
4
0
Если функция возрастает,
то производная
положительна
Если функция убывает,
то производная
отрицательна
График
функции
Слайд 11В7(ЕГЭ) На рисунке изображен график функции у = f(x) и
Слайд 12В7 (ЕГЭ) На рисунке изображен график функции у = f(x)
Слайд 13В7.егэ. На рисунке изображен график функции , определенной на интервале (-9;8). Определите количество целых точек, в
Слайд 14В7 (егэ). На рисунке изображен график функции , определенной на интервале (−6; 8).
Слайд 15В7(егэ). На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество
Слайд 16Задание 7 № 6871.На рисунке изображен график функции , определенной на интервале (-1;12) .Определите количество целых
Слайд 17Если f/(x) > 0,
значит, функция возрастает.
Если f/(x)
значит, функция убывает.
Признаки:
Задания В7 (ЕГЭ)
Графики производных
Слайд 18На рисунке изображен график y=f'(x) — производной функции f(x) , определенной
Если f/(x) > 0,
значит, функция возрастает.
График производной
Слайд 19Функция задана на отрезке. На рисунке изображен график ее производной.
Укажите количество
промежутков
возрастания функции.
b
а
Слайд 20На рисунке изображен график y=f'(x) — производной функции f(x), определенной
Если f/(x) < 0,
значит, функция убывает.
Слайд 21Функция задана на отрезке. На рисунке изображен график ее производной.
Укажите количество
убывания функции
b
а
Слайд 22b
а
На рисунке изображен график производной функции f(x),
определенной на интервале (a;b). Найдите
(1)
Слайд 23b
а
На рисунке изображен график производной функции f(x),
определенной на интервале (a;b). Найдите
(2)








![Исследование функции при помощи производной Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . В Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . В какой точке отрезка[-5;-1] функция принимает наибольшее значение.](/img/thumbs/d6313e47db21b09eeff3986ce0f0c985-800x.jpg)