- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Интерактивный плакат Формулы сокращённого умножения
Содержание
- 1. Интерактивный плакат Формулы сокращённого умножения
- 2. Формулы сокращенного умноженияФормулы сокращённого умножения многочленов — часто
- 3. История Некоторые правила сокращенного умножения были известны
- 4. Доказательство теоремы Пифагора Многое из Вавилона ушло потом
- 5. Примеры формулследующий слайдпредыдущий слайд
- 6. Применение формулследующий слайдпредыдущий слайд
- 7. Вывод формулКвадрат суммыАлгебраический способВозведем двучлен a +
- 8. Пример1) Умножим разность 3x - 7y на
- 9. 7 класс. Тест по теме: «Формулы сокращенного умножения»Начать тест
- 10. Результат тестаВерно: 6Ошибки: 4Отметка: 3Время: 0 мин. 25 сек.ещёисправитьзакончить
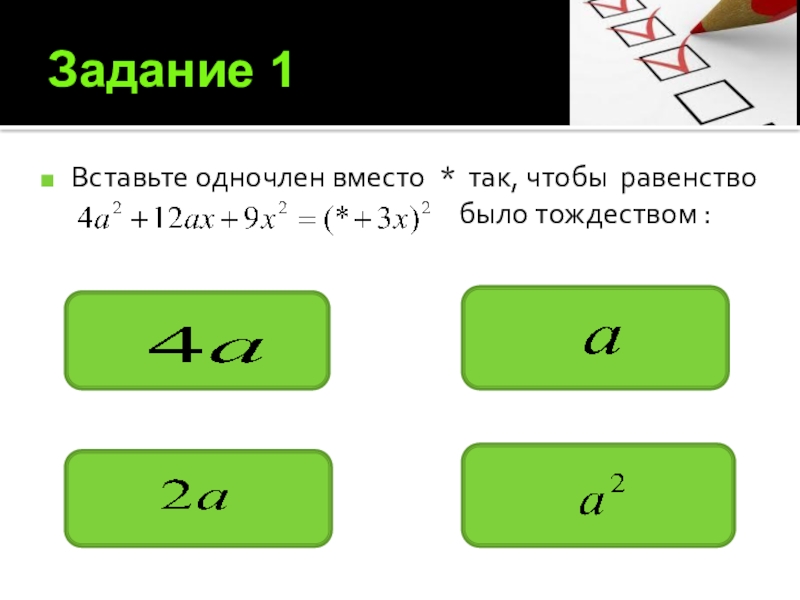
- 11. Задание 1 Вставьте одночлен вместо * так,
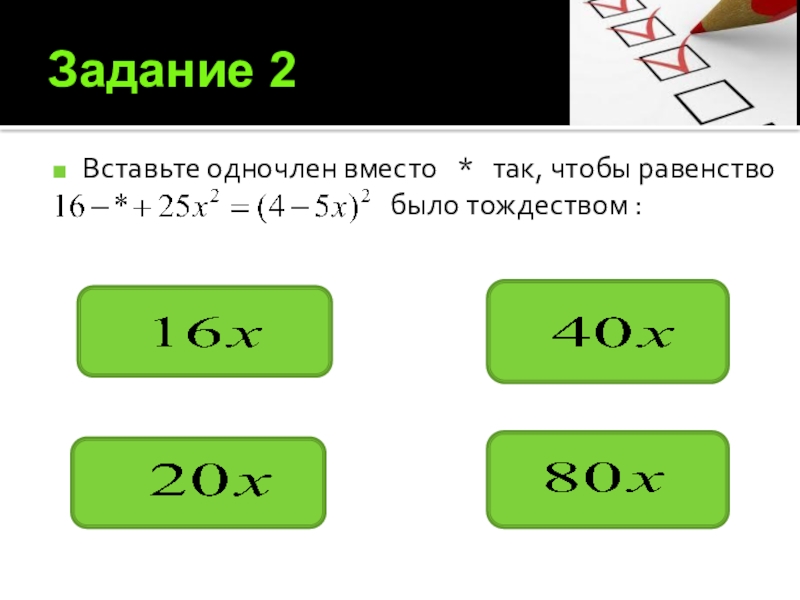
- 12. Задание 2Вставьте одночлен вместо *
- 13. Задание 3Выполните умножение
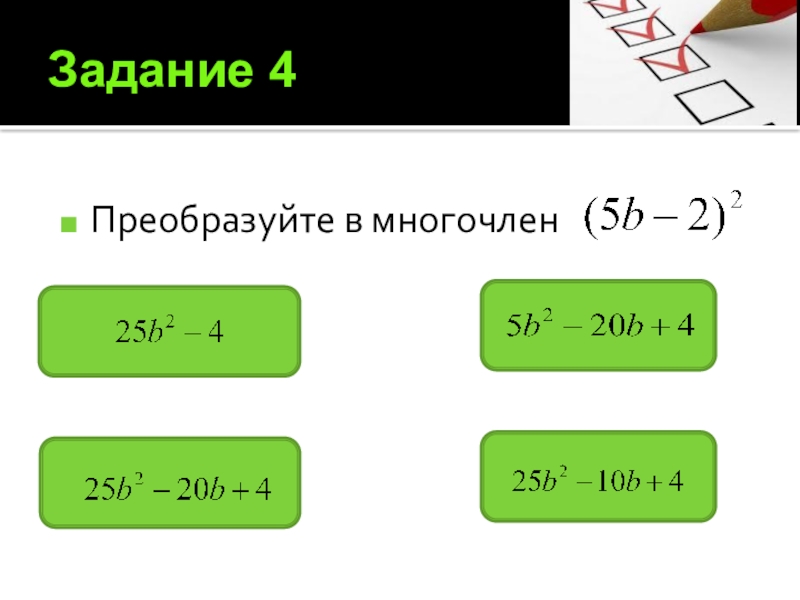
- 14. Задание 4Преобразуйте в многочлен
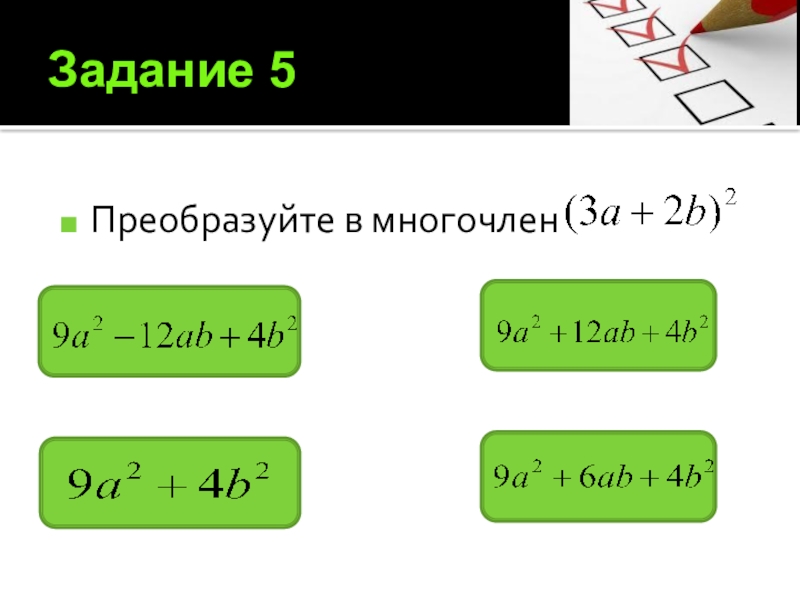
- 15. Задание 5Преобразуйте в многочлен
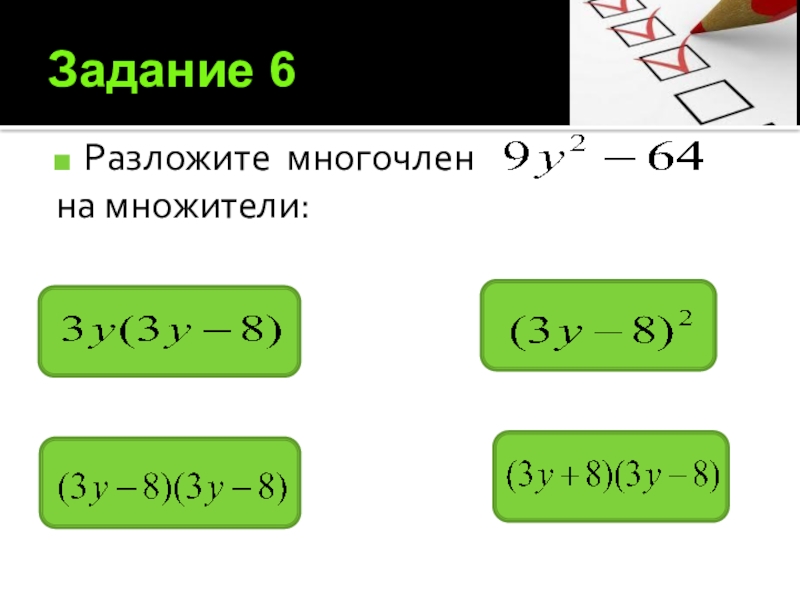
- 16. Задание 6Разложите многочлен на множители:
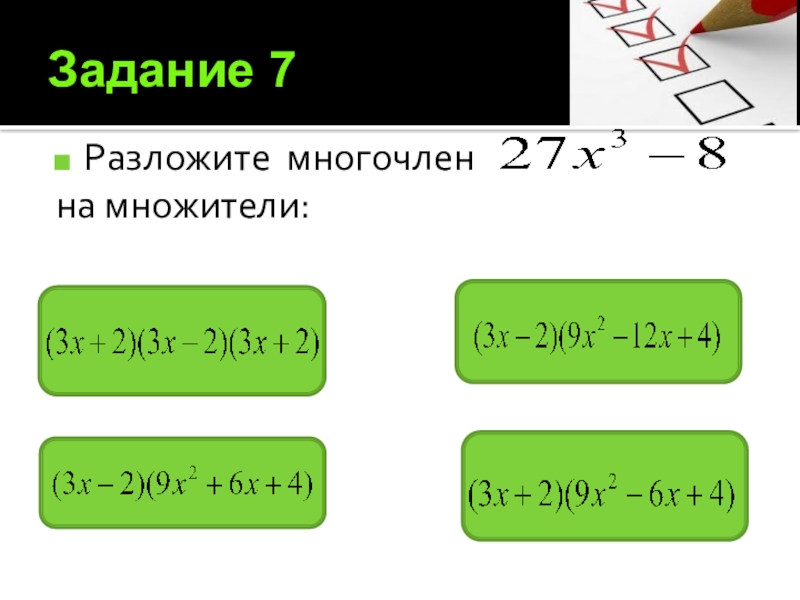
- 17. Задание 7Разложите многочлен на множители:
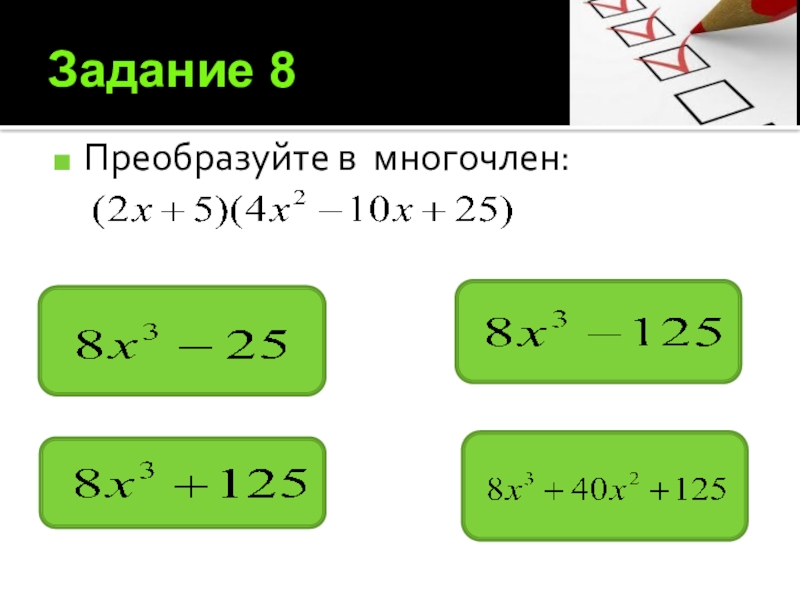
- 18. Задание 8Преобразуйте в многочлен:
- 19. Задание 9Выполните умножение
- 20. Задание 10Найдите значение выражения при = - 36, = 14-16-4164
- 21. Источники основного содержанияhttp://ru.wikipedia.org/wiki/Пифагорhttp://ru.wikipedia.org/wiki/Формулы_сокращённого умноженияwww.alleng.ru/d/math/math146.htmhttp://festival.1september.ru/articles/213381/следующий слайдеще раз тест
- 22. Источники иллюстрацийhttp://ru.wikipedia.org/wiki/Теорема_Пифагораhttp://www.varson.ru/alg_formula.htmlhttp://festival.1september.ru/articles/213381/предыдущий слайдв начало
Слайд 1Интерактивная математика в образовательных учреждениях XXI века
Никулина Ольга Александровна
МОУ «Средняя общеобразовательная
учитель математики
Слайд 2Формулы сокращенного умножения
Формулы сокращённого умножения многочленов — часто встречающиеся случаи умножения многочленов. Многие
следующий слайд
предыдущий слайд
Слайд 3История
Некоторые правила сокращенного умножения были известны еще около 4 тысяч
Правило, сформулированное во второй книге “Начал” Евклида в III веке до нашей эры, звучало так: “Если прямая линия как-либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключенным между отрезками”.
следующий слайд
предыдущий слайд
Слайд 4Доказательство теоремы Пифагора
Многое из Вавилона ушло потом в другие восточные страны,
Действительно, по рисунку видно, что
(a + b)2 = c2 + 4S∆
a2+2ab+b2 = c2 +2ab
c2 = a2 +b2
следующий слайд
предыдущий слайд
b2
а2
с2
Слайд 7Вывод формул
Квадрат суммы
Алгебраический способ
Возведем двучлен a + b в квадрат или
(a + b)2 = (a+b)(a+b) = a ∙ a + a ∙ b + b ∙ a + b ∙ b = a2 + a ∙ b + a ∙ b + b2 = a2 +2 ∙ a ∙ b + b2
Итак:
(a + b)2 = a2 +2 ∙ a ∙ b + b2
следующий слайд
предыдущий слайд
Слайд 8Пример
1) Умножим разность 3x - 7y на сумму 3x + 7y
2) Воспользуемся формулой произведения разности на сумму, получим: (3x-7y)(3x+7y)=(3x)2-(7y)2=9x2-49y2
3) Представим в виде многочлена произведение (5a2 - b3)(5a2 + b3)
4) Применим тождество, получим
(5a2 -b3)(5a2 +b3) = (5a2)2 -(b3)2 =25a4-b6
5) Представим в виде многочленов произведение
(-2a-9c)(2a-9c)
6) Вынесем в выражении -2a - 9c за скобки -1, тогда
(-2a-9c)(2a-9c)=(-1)(2a+9c)(2a-9c)=-1((2a)2-(9c)2) = - (4a2-81c2)= - 4a2+81c2 .
следующий слайд
предыдущий слайд