- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Интегративно - дифференцированный подход в обучении математики студентов (11 класс)
Содержание
- 1. Интегративно - дифференцированный подход в обучении математики студентов (11 класс)
- 2. Формула обучения «овладение = усвоение + применение знаний на практике»
- 3. Цель дифференциации процесса обучения –обеспечить каждому
- 4. Чешский педагог 17 века Ян Амос Коменский:
- 5. Основные правила технологии разноуровневого обученияОсновные правила технологии
- 6. В настоящее время перед
- 7. Качества, которыми должен обладать выпускник:- гибко адаптироваться
- 8. По данным исследований, в памяти
- 9. «Я услышал и забыл, я увидел и
- 10. Тренажер для устного счетаВычислить 1В.
- 11. Тренажер для устного счета. Вычислить.
- 12. Тематические тесты . Графики функций А5. График
- 13. Решение неравенств методом интервалов.А7. Решите неравенство А7. Решите неравенство
- 14. Нахождение множества значений функции. А8. Укажите множество значений
- 15. Тематические тесты . В1. Укажите наименьшее натуральное решение неравенства Решение неравенств методом интервалов..
- 16. Тематические тесты. Решить тригонометрическое уравнениеС1. Решите уравнение
- 17. Самостоятельная работа«Иррациональные уравнения»
- 18. Самостоятельная работа. «Логарифмические уравнения и неравенства»
- 19. Самостоятельная работа. «Объём пирамиды» Вариант 1Основание пирамиды
- 20. Задачи с профессиональной направленностьюПрофессия « Повар»Напиток «Летний»
- 21. Карточки-задания. Логарифмические неравенства
- 22. Олимпиада по математике 1. В один сосуд
- 23. РАЗРАБОТКА РАЗНОУРОВНЕВОГО УРОКА ПО АЛГЕБРЕ
- 24. Цель урока:Тип урока: закрепление изученного материала.Цели урока:
- 25. «Производная функции» Цели изучения урока распределяются по
- 26. Пояснительная запискаУчебные карты № 1 – 4
- 27. УЧЕБНая карта № 1Цель: закрепление темы «Производная»,
- 28. Таблица производных
- 29. Учебная карта № 1. Самостоятельная работа (
- 30. УЧЕБНая карта №2 Цель: закрепить умения находить
- 31. УЧЕБНая карта №3 Цель: Закрепить навык нахождения
- 32. УЧЕБНая карта №4 Цель: Закрепить навык нахождения
- 33. Учебная карта №5 Цель: Применять полученные знания
Формула обучения «овладение = усвоение + применение знаний на практике»
Слайд 1
«Дифференцированный подход в обучении математике
студентов»
(из опыта работы)
Преподаватель математики
Арзанова Ирина Геннадьевна
Слайд 3 Цель дифференциации процесса
обучения –обеспечить каждому
студенту условия для максимального
развития его способностей, склонностей,
удовлетворения познавательных
интересов, потребностей
в процессе освоения содержания
образования.
Слайд 4Чешский педагог 17 века Ян Амос Коменский:
«Мы решаемся обещать
Великую дидактику, т.е. универсальное искусство всех учить всему. И притом учить с верным успехом, так, чтобы неуспеха последовать не могло…»
Слайд 5Основные правила технологии разноуровневого обучения
Основные правила технологии разноуровневого обучения можно свести
к следующему:
1. Не дотягивать всех студентов до единого уровня, а создавать условия каждому в меру его потребностей, сил и желания.
2. Последовательное освоение и сдача уровней.
3. За одно занятие можно сдать только одну тему.
4. Для получения оценки «3» необходимо знание не менее 50 % из числа предложенных в данный период времени тем,
на «4» – 70–80 %, на «5» – 90–100 %.
5. При подготовке к практическому занятию можно выбрать любой уровень заданий и повысить свою обычную отметку.
6. Основными принципами являются: доброжелательность, взаимопомощь, нормотворчество, право на собственное мнение и ошибку.
1. Не дотягивать всех студентов до единого уровня, а создавать условия каждому в меру его потребностей, сил и желания.
2. Последовательное освоение и сдача уровней.
3. За одно занятие можно сдать только одну тему.
4. Для получения оценки «3» необходимо знание не менее 50 % из числа предложенных в данный период времени тем,
на «4» – 70–80 %, на «5» – 90–100 %.
5. При подготовке к практическому занятию можно выбрать любой уровень заданий и повысить свою обычную отметку.
6. Основными принципами являются: доброжелательность, взаимопомощь, нормотворчество, право на собственное мнение и ошибку.
Слайд 6 В настоящее время перед образованием стоит проблема -
подготовить студентов к жизни в современном обществе и профессиональной деятельности в высокоразвитой информационной среде, к возможности получения дальнейшего образования с использованием современных информационных технологий.
Слайд 7Качества, которыми должен обладать выпускник:
- гибко адаптироваться в меняющихся жизненных ситуациях,
самостоятельно приобретая необходимые знания, умело применяя их в практической деятельности;
- критически и творчески мыслить, четко осознавать, где и каким образом приобретаемые знания могут быть применены в окружающей действительности;
- самостоятельно работать над развитием собственного интеллекта, нравственности, физического состояния, культурным уровнем;
- грамотно работать с информацией (уметь собирать, анализировать, сопоставлять, обобщать, устанавливать закономерности, формулировать выводы и т.д.), в том числе с помощью компьютера и других средств информационных и коммуникационных технологий;
- быть коммуникабельным, уметь работать в различных группах.
- критически и творчески мыслить, четко осознавать, где и каким образом приобретаемые знания могут быть применены в окружающей действительности;
- самостоятельно работать над развитием собственного интеллекта, нравственности, физического состояния, культурным уровнем;
- грамотно работать с информацией (уметь собирать, анализировать, сопоставлять, обобщать, устанавливать закономерности, формулировать выводы и т.д.), в том числе с помощью компьютера и других средств информационных и коммуникационных технологий;
- быть коммуникабельным, уметь работать в различных группах.
Слайд 8 По данным исследований, в памяти человека остается:
* ¼
часть услышанного материала,
* ⅓ часть увиденного,
* ½ часть увиденного и
услышанного,
* ¾ части материала,
если студент привлечен в активные
действия в процессе обучения.
* ⅓ часть увиденного,
* ½ часть увиденного и
услышанного,
* ¾ части материала,
если студент привлечен в активные
действия в процессе обучения.
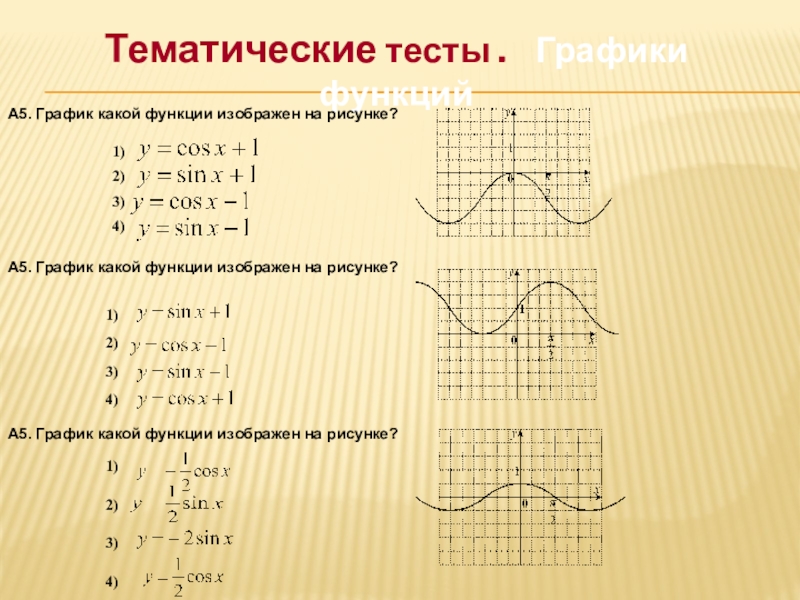
Слайд 12Тематические тесты . Графики функций
А5. График какой функции изображен на
рисунке?
А5. График какой функции изображен на рисунке?
А5. График какой функции изображен на рисунке?
Слайд 13Решение неравенств методом интервалов.
А7. Решите неравенство
А7. Решите неравенство
.
Тематические тесты .
А7. Решите неравенство
.
А7. Решите неравенство
.
Слайд 14Нахождение множества значений функции.
А8. Укажите множество значений функции
А8. Какое число не
входит в множество значений функции
А3. Из данных чисел выберите число, принадлежащее множеству значений функции
А6. Укажите область значений функции
.
Тематические тесты .
Слайд 15Тематические тесты .
В1. Укажите наименьшее натуральное решение неравенства
Решение неравенств методом
интервалов.
.
Слайд 19Самостоятельная работа. «Объём пирамиды»
Вариант 1
Основание пирамиды — ромб со стороной 4
м и острым углом 30°. Двугранные углы при основании пирамиды содержат по 45°. Найти объем пирамиды.
Вариант 2
Основанием пирамиды служит треугольник со сторонами 5 см, 12 см и 13 см. Каждое боковое ребро пирамиды наклонено к основанию под углом 45°. Найти объем пирамиды.
Вариант 3
В основании пирамиды — равнобедренная трапеция с боковой стороной 6 см и углом 30°. Боковые грани пирамиды наклонены к основанию под углом 60°. Найти объем пирамиды.
Вариант 2
Основанием пирамиды служит треугольник со сторонами 5 см, 12 см и 13 см. Каждое боковое ребро пирамиды наклонено к основанию под углом 45°. Найти объем пирамиды.
Вариант 3
В основании пирамиды — равнобедренная трапеция с боковой стороной 6 см и углом 30°. Боковые грани пирамиды наклонены к основанию под углом 60°. Найти объем пирамиды.
Слайд 20Задачи с профессиональной направленностью
Профессия « Повар»
Напиток «Летний» содержит 50% сои, 14%
ячменя, 30% свеклы, 6% шиповника. Определите массу каждой составляющей в 500 г такого напитка.
Печенье содержит 10% белка, 16% жира, 60% углеводов. Сколько белка, жира и углеводов содержится в 400 г такого печенья?
Ячмень содержит 60% крахмала, а рис-75%. Для приготовления крахмала взяли 400 г ячменя и 300 г риса. Из какого зерна крахмала получится больше?
При помоле пшеницы получается 80% муки, а при помоле ржи – 75%. Для помола взяли 4 ц пшеницы и 5 ц ржи. Какой муки получится меньше?
Печенье содержит 10% белка, 16% жира, 60% углеводов. Сколько белка, жира и углеводов содержится в 400 г такого печенья?
Ячмень содержит 60% крахмала, а рис-75%. Для приготовления крахмала взяли 400 г ячменя и 300 г риса. Из какого зерна крахмала получится больше?
При помоле пшеницы получается 80% муки, а при помоле ржи – 75%. Для помола взяли 4 ц пшеницы и 5 ц ржи. Какой муки получится меньше?
Слайд 22Олимпиада по математике
1. В один сосуд входит 3 л., а в
другой – 5 л. Как с помощью этих сосудов налить в кувшин 4 л. воды с водопроводного крана?
2. Я задумал число, прибавил к нему 1, умножил сумму на 2, произведение разделил на 3 и отнял от результата 4. Получилось 5. Какое число я задумал?
3. Дана дробь . Какое число нужно прибавить к обоим членам этой дроби, чтобы она обратилась в ?
4. При каких значениях х произведение (3х-5)(х+4)(2-х)
а) равно 0; б) положительно; в) отрицательно
5. На две партии разбившись, забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась,
Криком радостным двенадцать
Воздух свежий оглашали…
Вместе сколько, ты мне скажешь, обезьян там было в роще?
2. Я задумал число, прибавил к нему 1, умножил сумму на 2, произведение разделил на 3 и отнял от результата 4. Получилось 5. Какое число я задумал?
3. Дана дробь . Какое число нужно прибавить к обоим членам этой дроби, чтобы она обратилась в ?
4. При каких значениях х произведение (3х-5)(х+4)(2-х)
а) равно 0; б) положительно; в) отрицательно
5. На две партии разбившись, забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась,
Криком радостным двенадцать
Воздух свежий оглашали…
Вместе сколько, ты мне скажешь, обезьян там было в роще?
Слайд 23РАЗРАБОТКА РАЗНОУРОВНЕВОГО
УРОКА
ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА
тема: «Производная функции»
Преподаватель
математики
Арзанова И.Г.
Арзанова И.Г.
Слайд 24Цель урока:
Тип урока: закрепление изученного материала.
Цели урока:
Обеспечить повторение, обобщение и
систематизацию материала темы.
Способствовать формированию умений применять приемы обобщения, развитию математического кругозора, мышления, внимания и памяти, развивать самостоятельность, самоконтроль, аккуратность.
Воспитывать активность.
Способствовать формированию умений применять приемы обобщения, развитию математического кругозора, мышления, внимания и памяти, развивать самостоятельность, самоконтроль, аккуратность.
Воспитывать активность.
Слайд 25«Производная функции»
Цели изучения урока распределяются по трем уровням:
Уровень А -
самый общий т. е. знаниями этого уровня должны владеть все студенты;
Уровень В - включает все, что достигнуто на I уровне, но в более сложном виде;
Уровень С - включает все, что достигнуто на I и II уровнях, но теперь должно применяться в нестандартных ситуациях.
В результате овладения содержанием темы учащиеся должны уметь:
Уровень А- находить простейшие производные функций по формулам;
Уровень В - находить производные функций, самостоятельно выбирать метод решения;
Уровень С - применять полученные знания в нестандартных ситуациях.
Уровень В - включает все, что достигнуто на I уровне, но в более сложном виде;
Уровень С - включает все, что достигнуто на I и II уровнях, но теперь должно применяться в нестандартных ситуациях.
В результате овладения содержанием темы учащиеся должны уметь:
Уровень А- находить простейшие производные функций по формулам;
Уровень В - находить производные функций, самостоятельно выбирать метод решения;
Уровень С - применять полученные знания в нестандартных ситуациях.
Слайд 26Пояснительная записка
Учебные карты № 1 – 4 соответствуют уровням подготовки А
и В , № 5-уровню подготовки С.
Каждая учебная карта содержит указания преподавателя о том, что нужно знать и уметь, или краткие пояснения к выполнению заданий, или ссылки на учебник, где можно найти нужные объяснения, а также список заданий.
Прочитав указания преподавателя, студент выполняет самостоятельные работы, которые включены в карту, и проверяет их по эталонам решений. Эталон преподаватель демонстрирует студенту, когда тот объявляет о завершении самостоятельной работы. Студент сравнивает свои ответы с эталонными и исправляет ошибки.
Если он выполнил менее половины заданий, то решает задания другого варианта, которые аналогичны тем, в которых он допустил ошибки.
Каждая учебная карта содержит указания преподавателя о том, что нужно знать и уметь, или краткие пояснения к выполнению заданий, или ссылки на учебник, где можно найти нужные объяснения, а также список заданий.
Прочитав указания преподавателя, студент выполняет самостоятельные работы, которые включены в карту, и проверяет их по эталонам решений. Эталон преподаватель демонстрирует студенту, когда тот объявляет о завершении самостоятельной работы. Студент сравнивает свои ответы с эталонными и исправляет ошибки.
Если он выполнил менее половины заданий, то решает задания другого варианта, которые аналогичны тем, в которых он допустил ошибки.
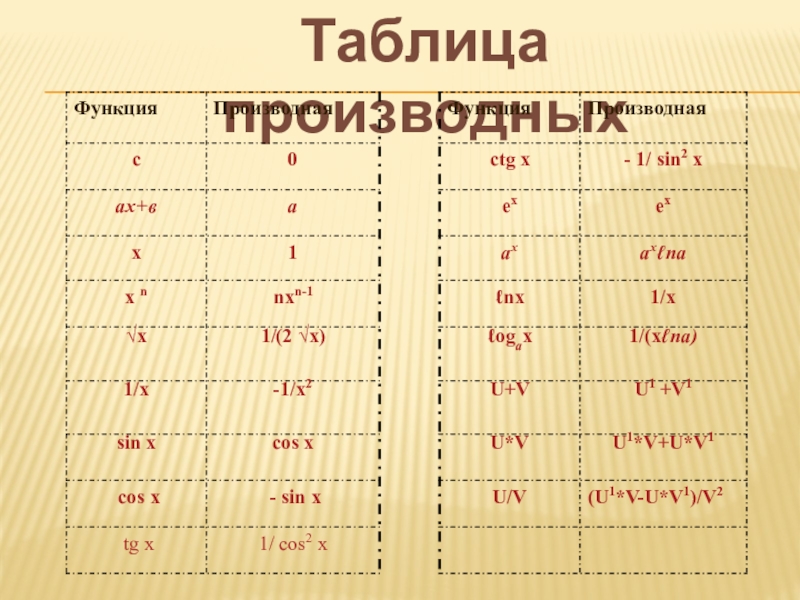
Слайд 27УЧЕБНая карта № 1
Цель: закрепление темы «Производная», отработка навыков нахождение простых
производных по формулам
Указания преподавателя: Вспомните основные правила вычисления производных.
Таблица производных прилагается.
(Прочитайте текст на стр. 113-116 учебника под редакцией А. Н. Колмогорова)
Указания преподавателя: Вспомните основные правила вычисления производных.
Таблица производных прилагается.
(Прочитайте текст на стр. 113-116 учебника под редакцией А. Н. Колмогорова)
Слайд 29Учебная карта № 1.
Самостоятельная работа ( 15 мин)
Найти производные фунцкий:
1 вариант 2 вариант
f(x)=25 f(x)=19
f(x)=4x f(x)=3x
f(x)=8x2 f(x)=7x3
f(x)=x14 f(x)=x6
f(x)=17x3 f(x)=10x2
f(x)=10x2 f(x)=x-2
f(x)=x2+6x f(x)=x3+8x
f(x)=x5-7x2+8 f(x)=x2+3x-1
f(x)=7ех-2ах f(x)= 3ех-5ах
f(x)=3ℓnх f(x)=5ℓnх
f(x)=25 f(x)=19
f(x)=4x f(x)=3x
f(x)=8x2 f(x)=7x3
f(x)=x14 f(x)=x6
f(x)=17x3 f(x)=10x2
f(x)=10x2 f(x)=x-2
f(x)=x2+6x f(x)=x3+8x
f(x)=x5-7x2+8 f(x)=x2+3x-1
f(x)=7ех-2ах f(x)= 3ех-5ах
f(x)=3ℓnх f(x)=5ℓnх
Слайд 30УЧЕБНая карта №2
Цель: закрепить умения находить производные функции по формулам произведения
и дроби.
Указания преподавателя: Вспомните правила вычисления производных по правилу №2 и №3 учебник А. Н. Колмогорова (стр. 114).
(U * V)'=U'V+UV'
(U/V)'=(U'V - UV')/V2
Самостоятельная работа №2 (на 15 минут)
Найдите производную функции и вычислите ее значения при Х , равном -1 и 1 , если
I вариант II вариант
f(x)=(3x-4)(2x+5) f(x)=(2x-3)(1-x2)
f(x)=x2(8+7x-x3) f(x)=x3(4+2x-x2)
У=(2х-3)/(5-6х) У=(4х+2)/(7-4х)
У=(5-2х)/(1+3х2) У=(2х-3)/(4-5х2)
Указания преподавателя: Вспомните правила вычисления производных по правилу №2 и №3 учебник А. Н. Колмогорова (стр. 114).
(U * V)'=U'V+UV'
(U/V)'=(U'V - UV')/V2
Самостоятельная работа №2 (на 15 минут)
Найдите производную функции и вычислите ее значения при Х , равном -1 и 1 , если
I вариант II вариант
f(x)=(3x-4)(2x+5) f(x)=(2x-3)(1-x2)
f(x)=x2(8+7x-x3) f(x)=x3(4+2x-x2)
У=(2х-3)/(5-6х) У=(4х+2)/(7-4х)
У=(5-2х)/(1+3х2) У=(2х-3)/(4-5х2)
Слайд 31УЧЕБНая карта №3
Цель: Закрепить навык нахождения производных тригонометрических функций.
Указания преподавателя: Внимательно
прочитайте п. 17 учебника
А. Н. Колмогорова стр. 121.
Вспомните производные синуса, косинуса, тангенса и котангенса.
(sin x)'=cosx (cos x)'=- sinx
(tg x)'=1/cos2x (сtg x)'=-1/sin2x
Самостоятельная работа №3 (на 15 минут)
Найдите производную каждой из функций.
I вариант II вариант
y=2sin x y=-0,5sin x
y=1-cos x y=2-3cos x
y= tg x y=4ctg x
y=2sin x+5cos x y=3cos x - 4sin x
y=(3+4cos x)(5-3sin x) y=(1-2sin x)(2-cos x)
y=5ctg x-4х y= 3tg x+5х
А. Н. Колмогорова стр. 121.
Вспомните производные синуса, косинуса, тангенса и котангенса.
(sin x)'=cosx (cos x)'=- sinx
(tg x)'=1/cos2x (сtg x)'=-1/sin2x
Самостоятельная работа №3 (на 15 минут)
Найдите производную каждой из функций.
I вариант II вариант
y=2sin x y=-0,5sin x
y=1-cos x y=2-3cos x
y= tg x y=4ctg x
y=2sin x+5cos x y=3cos x - 4sin x
y=(3+4cos x)(5-3sin x) y=(1-2sin x)(2-cos x)
y=5ctg x-4х y= 3tg x+5х
Слайд 32УЧЕБНая карта №4
Цель: Закрепить навык нахождения производной сложной функции
Указания преподавателя: Внимательно
прочитать п. 16 стр.118 учебника А. Н. Колмогорова. Разобрать решение примеров
№1, №2, №3.
F'(g(х)) = F'(g) g'(х)
Самостоятельная работа №4 (на 15 минут)
Найдите производную каждой из функций.
1 вариант 2 вариант
f(x)=(2x-7)8 f(x)=(9x+5)4
f(x)=(x3-2x2+3)17 f(x)=(x3+4x2-8)15
f(x)= 1/(3х2-5) f(x)= 1/(3-2х2)
f(x)= е3х-2*54х f(x)= е2х+4 *27х
f(x)= ℓоg3(6х-1) f(x)= ℓоg5(2-5х)
№1, №2, №3.
F'(g(х)) = F'(g) g'(х)
Самостоятельная работа №4 (на 15 минут)
Найдите производную каждой из функций.
1 вариант 2 вариант
f(x)=(2x-7)8 f(x)=(9x+5)4
f(x)=(x3-2x2+3)17 f(x)=(x3+4x2-8)15
f(x)= 1/(3х2-5) f(x)= 1/(3-2х2)
f(x)= е3х-2*54х f(x)= е2х+4 *27х
f(x)= ℓоg3(6х-1) f(x)= ℓоg5(2-5х)
Слайд 33Учебная карта №5
Цель: Применять полученные знания в вычислении производных в нестандартной
ситуации
Указания преподавателя: Вы прошли I и II уровень усвоения материала.
Теперь вам самостоятельно придется выбирать правила нахождения производных функций. Необходимо вспомнить весь материал по нахождению простых и сложных функций.
Прочтите текст учебника А. Н. Колмогорова п. 15-17 стр.113-123.
Самостоятельная работа №5 (на 20 минут)
I вариант II вариант
Найдите значения производных следующих функций в точках х=0 и х=2
y=(5-2x4)7 y=(5-7х3)10
y=( 7-8x2)11 +4х y=(х2+3)4 - 5х
у=(1+3х)4/(5х+1) у=(2-5х)3/(4х-3)
Найдите производную функции
у=3Sin2 (2х-3) у=5cos2(3х-1)
у=4ℓog26(х3-5) у=3 ℓog24(2-3х2)
Домашнее задание.
Выполните из учебника под редакцией А. Н. Колмогорова № 208, 209, 231, 232, 224(a, в).
Указания преподавателя: Вы прошли I и II уровень усвоения материала.
Теперь вам самостоятельно придется выбирать правила нахождения производных функций. Необходимо вспомнить весь материал по нахождению простых и сложных функций.
Прочтите текст учебника А. Н. Колмогорова п. 15-17 стр.113-123.
Самостоятельная работа №5 (на 20 минут)
I вариант II вариант
Найдите значения производных следующих функций в точках х=0 и х=2
y=(5-2x4)7 y=(5-7х3)10
y=( 7-8x2)11 +4х y=(х2+3)4 - 5х
у=(1+3х)4/(5х+1) у=(2-5х)3/(4х-3)
Найдите производную функции
у=3Sin2 (2х-3) у=5cos2(3х-1)
у=4ℓog26(х3-5) у=3 ℓog24(2-3х2)
Домашнее задание.
Выполните из учебника под редакцией А. Н. Колмогорова № 208, 209, 231, 232, 224(a, в).