- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Графики и функции вокруг нас
Содержание
- 1. Графики и функции вокруг нас
- 2. Функции вида y=kx y=kx+bПри k>0 график линейной
- 3. Функции вида y=kx y=kx+b у=kx
- 4. Линейная функция y=bПри k=0 линейная функция имеет вид y=b и график её параллелен оси абцисс
- 5. Чтобы выяснить геометрический смысл коэффициента k можно
- 6. Построение функций:а) y=2x+4 б)
- 7. Не вычерчивая графиков функции, установите под острым,
- 8. Геометрический смысл коэффициента b также можно установить
- 9. Построение функций:а) y=3x+4 б) y=3x-4 в)
- 10. Взаимное расположение графиков линейных функций:Графики двух линейных
- 11. Пример:Задайте формулами функции, графики которых:а) параллельные прямые
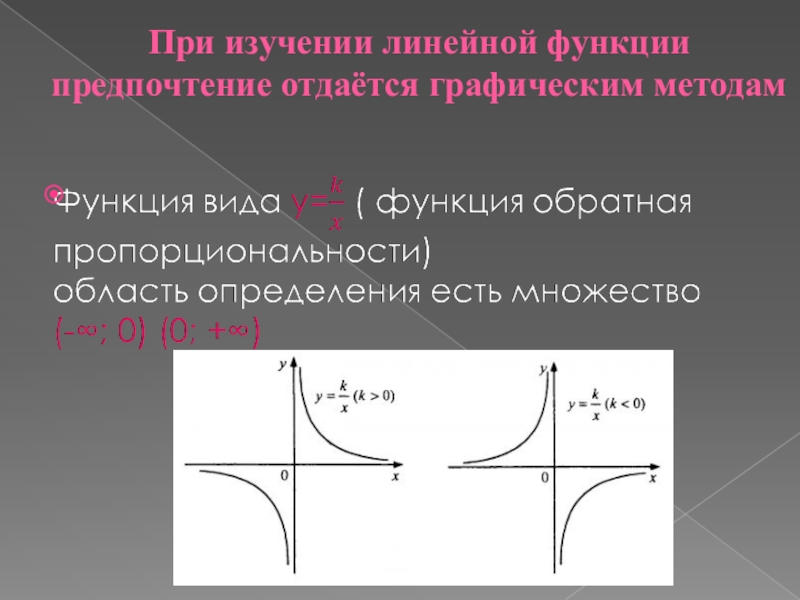
- 12. При изучении линейной функции предпочтение отдаётся графическим методам
- 13. На интервалах (-∞;0) и (0; +∞), но
Функции вида y=kx y=kx+bПри k>0 график линейной функции составляет острый угол с положительным направлением оси абцисс, а при k0
Слайд 2Функции вида
y=kx
y=kx+b
При k>0 график линейной функции составляет острый угол с положительным
направлением оси абцисс, а при k<0 – тупой угол
y=kx y=kx+b
k>0 k>0
угол угол
острый острый
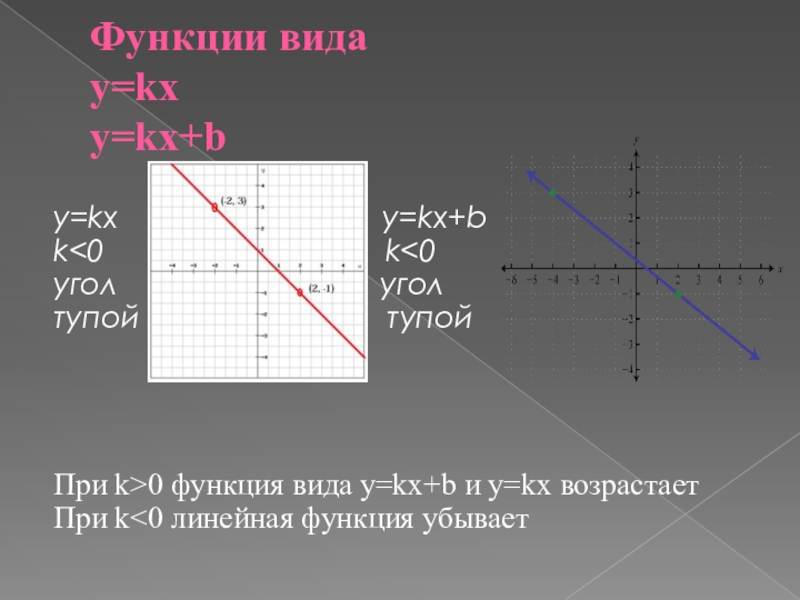
Слайд 3Функции вида
y=kx
y=kx+b
у=kx
y=kx+b
k<0 k<0
угол угол
тупой тупой
При k>0 функция вида y=kx+b и y=kx возрастает
При k<0 линейная функция убывает
Слайд 5Чтобы выяснить геометрический смысл коэффициента k можно рассмотреть следующие задания
Пример:
а) y=2x+4
б) y=2x-4
в) y= -2x+4 г) y= -2x-4
Не строя графиков выясните, в каком случае значение y возрастают (убывают) с возрастанием x , затем постройте графики и проверьте на них свои ответы
Не строя графиков выясните, в каком случае значение y возрастают (убывают) с возрастанием x , затем постройте графики и проверьте на них свои ответы
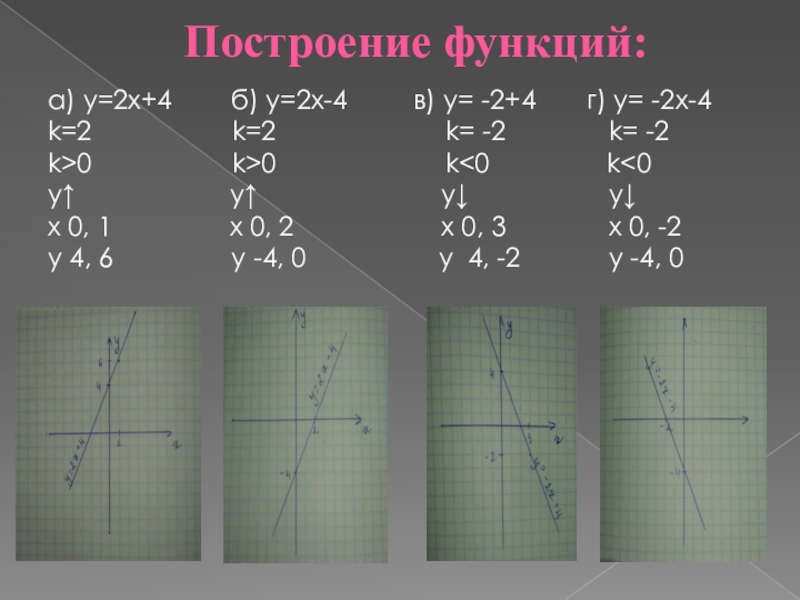
Слайд 6Построение функций:
а) y=2x+4 б) y=2x-4
в) y= -2+4 г) y= -2x-4
k=2 k=2 k= -2 k= -2
k>0 k>0 k<0 k<0
y↑ y↑ y↓ y↓
x 0, 1 x 0, 2 x 0, 3 x 0, -2
у 4, 6 y -4, 0 y 4, -2 y -4, 0
Слайд 7Не вычерчивая графиков функции, установите под острым, тупым или нулевым углом
они наклонены к положительному направлению оси абцисс:
Пример:
а) y=x
k=1; k>0 угол острый
б) y= -x+2
k=-1; k<0 угол тупой
в) y=3
k=0 угол=0
г) y= 2.5x-4
k=2.5; k>0 угол острый
Слайд 8Геометрический смысл коэффициента b также можно установить графически
Пример:
а) y=3x+4
б) y=3x-4
в) y=
-3x+4
г) y= -3x-4
Постройте графики функций и выясните, в каком случае прямая пересекает ось y выше оси x и ниже оси x
Постройте графики функций и выясните, в каком случае прямая пересекает ось y выше оси x и ниже оси x
Слайд 9Построение функций:
а) y=3x+4 б) y=3x-4 в) y=-3x=4 г)
y=-3x+4
x 0, 1 x 0, 2 x 0, 2 x 0, -3
y 4, 7 y -4, 2 y 4, -2 у -4, 5
Если b>0, график пересекает ось y выше оси x Если b<0, график пересекает ось y ниже оси x
Если b>0, график пересекает ось y выше оси x Если b<0, график пересекает ось y ниже оси x
Слайд 10Взаимное расположение графиков линейных функций:
Графики двух линейных функций, заданных формулами вида
y=kx+b, пересекаются, если коэффициенты при x различны, и параллельны, если коэффициенты при x одинаковы
Слайд 11Пример:
Задайте формулами функции, графики которых:
а) параллельные прямые
б) пересекающиеся
прямые
а) y=3x+5
y=3x-5
б) y=4x+3 y=2x-3
б) y=4x+3 y=2x-3
Слайд 13На интервалах (-∞;0) и (0; +∞), но не является убывающей на
всей области определения, это немонотонная функция