- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Фракталы
Содержание
- 1. Фракталы
- 2. Слайд 2
- 3. СОДЕРЖАНИЕ 1. Введение…………………………………………………………………… стр. 32. История появления
- 4. История появления фракталовЕвклидова геометрия
- 5. Что общего у дерева, берега моря, облака
- 6. Бенуа́ Мандельбро́т — французский и американский математик,
- 7. . Береговые линии обычно имеют фрактальную форму,
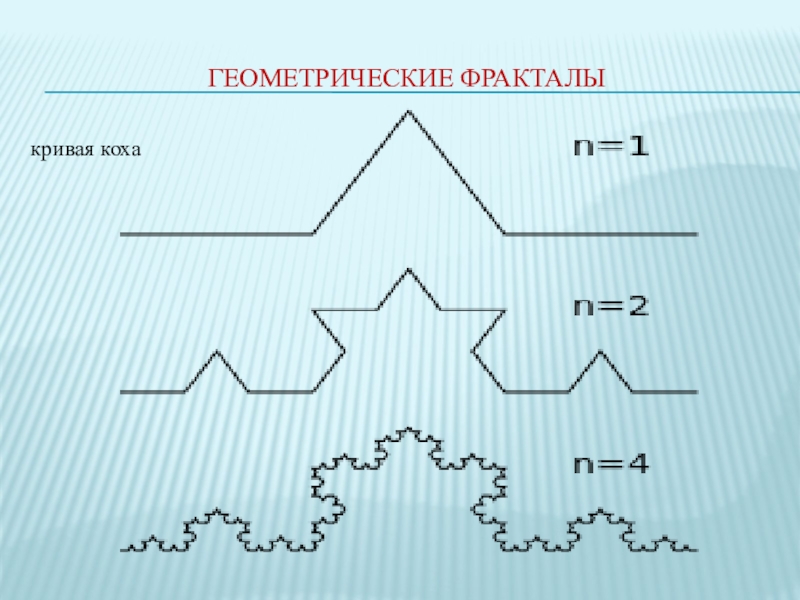
- 8. Геометрические фракталы кривая коха
- 9. Алгеброические фракталыстроятся на основе алгебраических формул. К
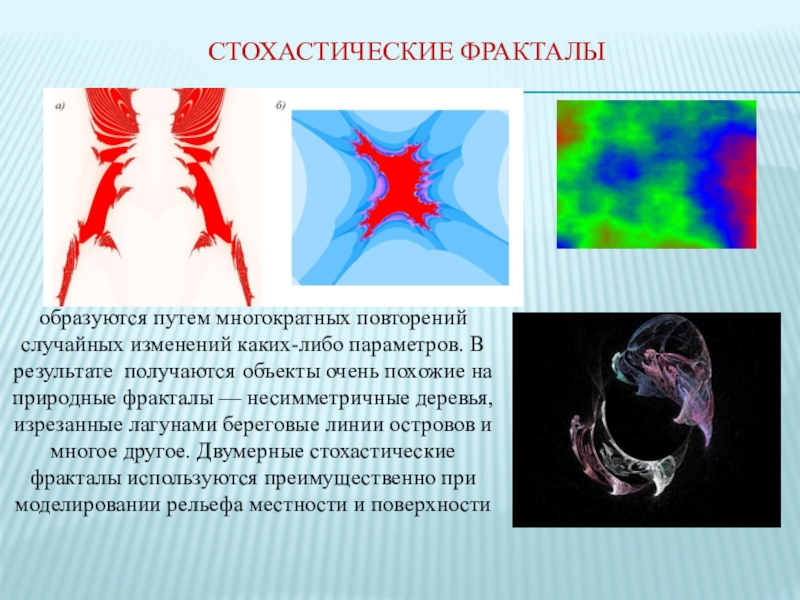
- 10. Стохастические фракталыобразуются путем многократных повторений случайных изменений
- 11. Фракталы в природеВы задумывались когда-нибудь, что мы
- 12. Фракталы на кухне
- 13. Фракталы в море
- 14. Комнатное растение -декабрист
- 15. .Летом на песке часто можно увидеть такой
- 16. Лист- естественный природный фрактал. Рисунок каждого листа неповторим
- 17. Фракталы на клумбе
- 18. Слайд 18
- 19. кактус
- 20. Сосновая шишка
- 21. Русские матрёшки
- 22. Евклидова геометрия в жизни
- 23. Применение фракталовФракталы находят все большее и большее
- 24. Спасибо за внимание
Слайд 1
III районная математическая конференция школьников
Никольского района
«Математика на службе человека»
Бесподобные
Фракталы
Работу выполнили:
Никонов Никита Витальевич,
Щукина Анастасия Евгеньевна
учащиеся 8 «Б» класса
МБОУ «Б-Курьевская ООШ»
Руководитель:
Подольская Валентина Зосимовна
учитель математики и физики
МБОУ «Б-Курьевская ООШ»
1 квалификационная категория
2017 г.
Слайд 2
1.ВВЕДЕНИЕ
Математика
Только эту красоту надо увидеть.
Б. Мандельброт
Гипотеза - все, что существует в реальном мире, является фракталом,
Цель - показать красоту математики.
Объектом исследования выступают фракталы в математике и в реальном мире.
В процессе работы нами были выделены следующие
задачи исследования:
- Дать определение фрактала,
- Познакомиться с историей появления фракталов,
- Узнать, какие типы фракталов существуют,
- Дать представление о фракталах, встречающихся в нашей жизни.
- Изобразить простейшие фракталы,
- Подготовить презентацию и выступить с докладом перед одноклассниками..
Слайд 3СОДЕРЖАНИЕ
1. Введение…………………………………………………………………… стр. 3
2. История появления фракталов…………………………………… стр. 5
3. Классификация
4. Фракталы в природе…………………………………………………… стр. 6
5. Применение фракталов…………………………………………………стр.7
5. Заключение ……………………………………………………………….. стр. 9
6. Список литературы…………………………………………………... стр. 11
7. Приложения …………………………………………………………... стр. 10
Слайд 5Что общего у дерева, берега моря, облака или кровеносных сосудов ?
Слайд 6Бенуа́ Мандельбро́т — французский и американский математик, создатель фрактальной геометрии. Лауреат
Вплоть до 20 века шло накопление данных о таких странных объектах. Так было, пока за них не взялся Бенуа Мандельброт - отец современной фрактальной геометрии и слова фрактал.
Что же такое фрактал. Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый. И одно из определений фрактала - это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого .
Слайд 7. Береговые линии обычно имеют фрактальную форму, но различаются степенью своей
-Отдельные протоки не являются копией друг друга, но имеют аналогичные криволинейные очертания,
-Большие протоки аналогичны по очертаниям маленьким . Если мы увеличим, например, нижний левый угол картинки, мы получим нечто похожее на всю картинку целиком
Слайд 9Алгеброические фракталы
строятся на основе алгебраических формул. К ним можно отнести фрактал
Слайд 10Стохастические фракталы
образуются путем многократных повторений случайных изменений каких-либо параметров. В результате
Слайд 11Фракталы в природе
Вы задумывались когда-нибудь, что мы буквально мыслим фракталами?
Мозг
Слайд 15.
Летом на песке часто можно увидеть такой рисунок. В крошечных масштабах
Слайд 23Применение фракталов
Фракталы находят все большее и большее применение в науке. Основная
-О дни из наиболее мощных приложений фракталов лежат в компьютерной графике. Это фрактальное сжатие изображений.
-В механике и физике фракталы используются благодаря уникальному свойству повторять очертания многих объектов природы. Фракталы позволяют приближать деревья, горные поверхности и трещины с более высокой точностью