«Аксуского колледжа черной металлургии»:
Шабалина Н.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Электронное учебное пособие по алгебре и начала анализа Логарифмы
Содержание
- 1. Электронное учебное пособие по алгебре и начала анализа Логарифмы
- 2. Слайд 2
- 3. Активизация познавательной деятельности обучающихся
- 4. Тригонометрия Тригонометрия–математическая дисциплина, изучающая зависимость между
- 5. СодержаниеОпределениеГрафики и свойства функцийМеры угловФормулыОсновные тождестваКонтрольТесты
- 6. Тригонометрия .Определение тригонометрических функцийy = sinxy = cosxy = tgxНесерьезная шпаргалкаВидео «Основы тригонометрии»
- 7. Вспомним:авсСинус острого угла в прямоугольном треугольнике
- 8. ху11
- 9. Синус угла определяется как ордината точки
- 10. 11-1-1Содержание
- 11. Радианная мера углаRС
- 12. Градусная и радианная меры угловЗначения тригонометрических функций на окружности..mp4Радианная мера углов
- 13. Задания 1.Выразите в радианной мере величины углов:А)
- 14. Задание 2.Выразите в градусной мере величины углов:А)
- 15. Координаты
- 16. Задание 1. Вычислитеа)б)в)Координаты
- 17. Тригонометрия .Тригонометрические функции, графики и свойстваy = sinxy = cosxy = tgxПостроение графиков
- 18. Слайд 18
- 19. Слайд 19
- 20. Функция y = tg x, её
- 21. Тригонометрия .Основные тождества тригонометрических функцийy = sinxy = cosxy = tgx
- 22. СодержаниеЗАДАНИЯ 1 2
- 23. Задания 1. Упростите выраженияа)б)в)г)д)Тождества
- 24. Задание 2.Найдите значения других трёх основных тригонометрических функций, если Тождества
- 25. Тригонометрия .Формулытригонометрических функцийФормулы двойного аргументаПреобразование сумм
- 26. Формулы двойного аргумента 1.sin2x = 2 sinx·cosx;2.cos2x
- 27. Задание 1. Упростите выражениеа)б)в)Формулы
- 28. Формулы сложения
- 29. Вычислитеа)б)в)Упроститеа)б)Формулы
- 30. Преобразование сумм тригонометрических функций в произведение1.2.3.4.
- 31. Задание 1. Вычислить: sin 75°+ sin 15°sin 75°- sin 15° Формулы
- 32. Задание 2. Упростите выражениеа)б)в)г) Формулы
- 33. ФормулыЗадания 1.Упростите выражения
- 34. tg2 х (sin2 х-1);2. cos2 х –
- 35. Задания 3.Составь соответствие:
- 36. Задания 3.Ответы:Формулы
- 37. КонтрольСодержание
- 38. ЛитератураА. Е. Абылкасимов, А. М. Абрамов «Алгебра
В электронном учебном пособии «Тригонометрия» разработан необходимый материал по формированию
Слайд 1«ТРИГОНОМЕТРИЯ»
Электронное учебное пособие
по математике
по теме
Автор: преподаватель математики
Слайд 2
В электронном учебном пособии «Тригонометрия»
разработан необходимый материал по формированию
основных знаний, умений и навыков студентов по разделу «Алгебра и начало анализа» общеобразовательных дисциплин.
В электронное пособие вошел материал по тригонометрии, изучающий определение тригонометрических функций, их графики и свойства, понятие радианой меры, основные тождества и формулы. Каждый раздел содержит краткий обзор теоретического материала, также имеются задания на знания перевода единиц угловых мер, упрощение тригонометрических выражений, тестовый контроль знаний, видеоматериалы.
Электронное учебное пособие может использоваться, как при теоретическом и практическом обучении студентов учебных заведений, так и при самостоятельном повышении качества знаний по теме «Тригонометрия».
разработан необходимый материал по формированию
основных знаний, умений и навыков студентов по разделу «Алгебра и начало анализа» общеобразовательных дисциплин.
В электронное пособие вошел материал по тригонометрии, изучающий определение тригонометрических функций, их графики и свойства, понятие радианой меры, основные тождества и формулы. Каждый раздел содержит краткий обзор теоретического материала, также имеются задания на знания перевода единиц угловых мер, упрощение тригонометрических выражений, тестовый контроль знаний, видеоматериалы.
Электронное учебное пособие может использоваться, как при теоретическом и практическом обучении студентов учебных заведений, так и при самостоятельном повышении качества знаний по теме «Тригонометрия».
Слайд 3Активизация познавательной деятельности обучающихся на уроках математики в
процессе применения электронного учебника.
Обучение пониманию изучаемого материала за счет информационно - коммуникационных технологий.
Формирование устойчивого интереса к учебе, к знаниям и потребности в их самостоятельном поиске.
Обучение пониманию изучаемого материала за счет информационно - коммуникационных технологий.
Формирование устойчивого интереса к учебе, к знаниям и потребности в их самостоятельном поиске.
Цель:
Слайд 4Тригонометрия
Тригонометрия–математическая дисциплина, изучающая зависимость между сторонами и углами треугольника. Слово
«тригонометрия» составлено из греческих слов: «тригонон» - треугольник и «метрео» - измеряю, что означает «измерение треугольников». Основная задача тригонометрии состоит в решении треугольников, т.е. в вычислении неизвестных величин треугольника по данным значениям других его величин.
Термин тригонометрия был впервые введён в 1595 году немецким богословом – математиком Варфоломеем Питиском. Так как любую вычислительную задачу геометрии можно свести к решению треугольников, то тригонометрия охватывает всю планиметрию и стереометрию и широко применяется во всех областях естествознания и техники.
Термин тригонометрия был впервые введён в 1595 году немецким богословом – математиком Варфоломеем Питиском. Так как любую вычислительную задачу геометрии можно свести к решению треугольников, то тригонометрия охватывает всю планиметрию и стереометрию и широко применяется во всех областях естествознания и техники.
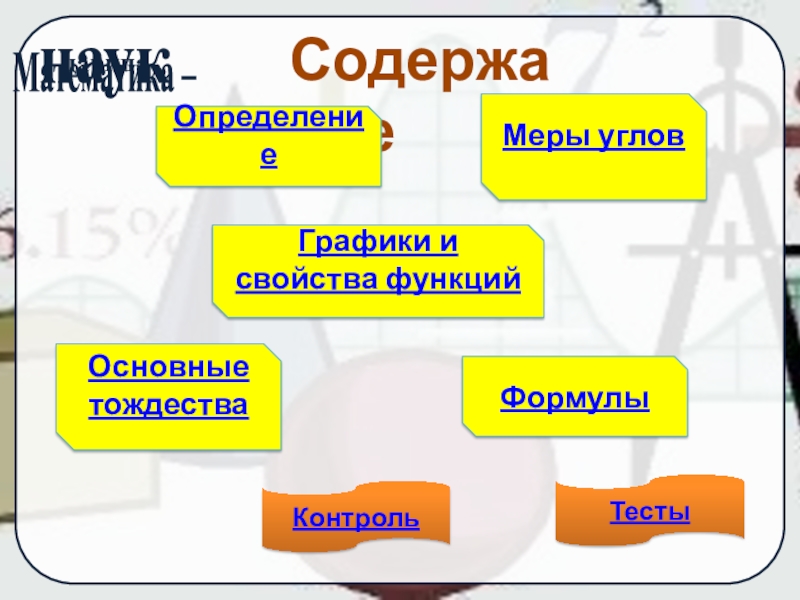
Слайд 5Содержание
Определение
Графики и свойства функций
Меры углов
Формулы
Основные тождества
Контроль
Тесты
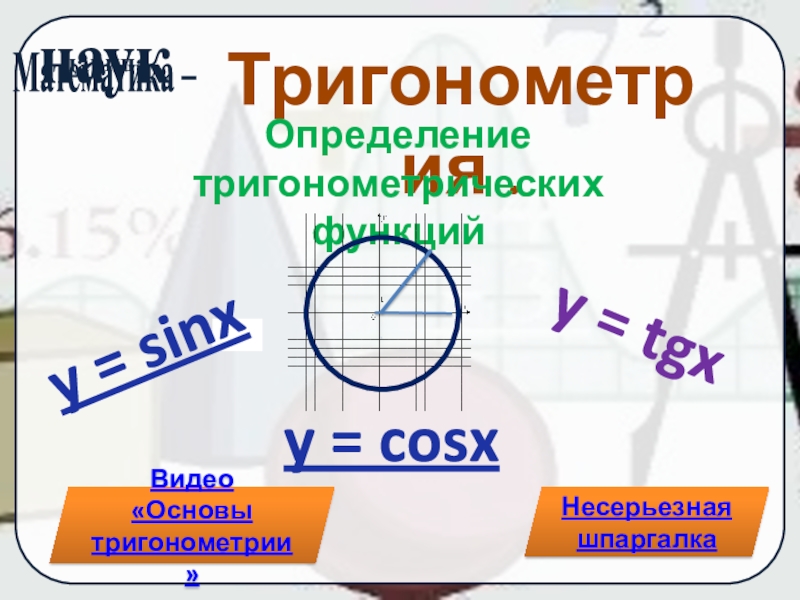
Слайд 6Тригонометрия .
Определение тригонометрических функций
y = sinx
y = cosx
y = tgx
Несерьезная шпаргалка
Видео
«Основы тригонометрии»
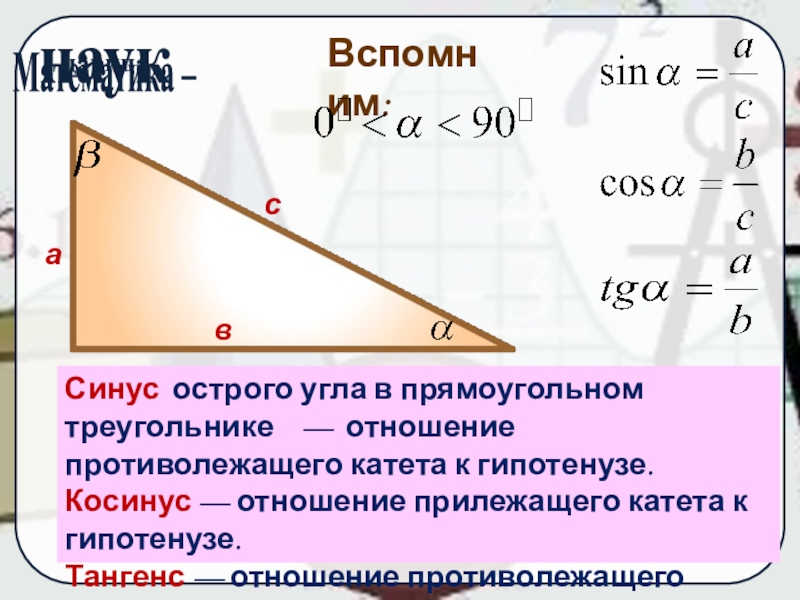
Слайд 7Вспомним:
а
в
с
Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета
к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.
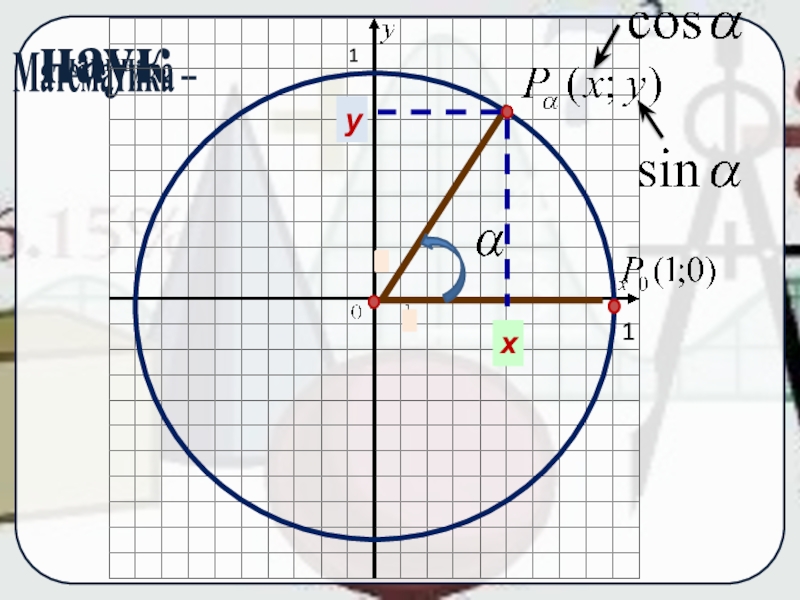
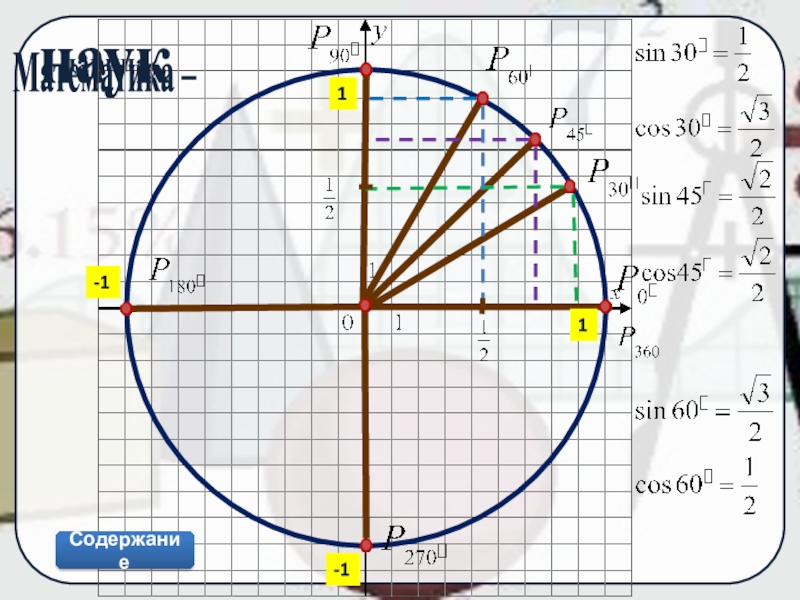
Слайд 9Синус угла определяется как ордината
точки
Косинус — абсцисса точки
Тангенс – отношение ординаты к абсциссе
точки
Котангенс – отношение абсциссы к ординате
точки
Слайд 11Радианная мера угла
R
С
центральный угол
R – радиус
С – длина дуги
Если R = C,
то центральный угол равен
одному радиану
Радианной мерой угла называется отношение длины соответствующей дуги
к радиусу окружности
ЗАДАНИЯ 1 2.
Координаты
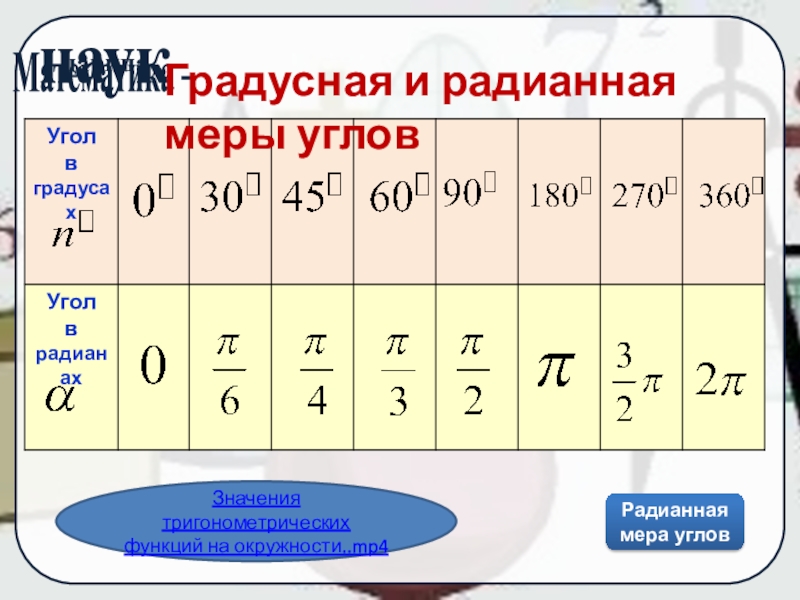
Слайд 12Градусная и радианная меры углов
Значения тригонометрических функций на окружности..mp4
Радианная мера углов
Слайд 13Задания 1.
Выразите в радианной мере
величины углов:
А) 45°; 36°; 180°;
Б) 60°;
72°; 270°;
В) 120°; 310°; 360°;
Г) 150°; 216°; 90°.
Пример: если α = 150°:
150°=
В) 120°; 310°; 360°;
Г) 150°; 216°; 90°.
Пример: если α = 150°:
150°=
Радианная мера углов
Слайд 14Задание 2.
Выразите в градусной мере
величины углов:
А)
Б)
В)
Например: если α = Г)
В)
Например: если α = Г)
Радианная мера углов
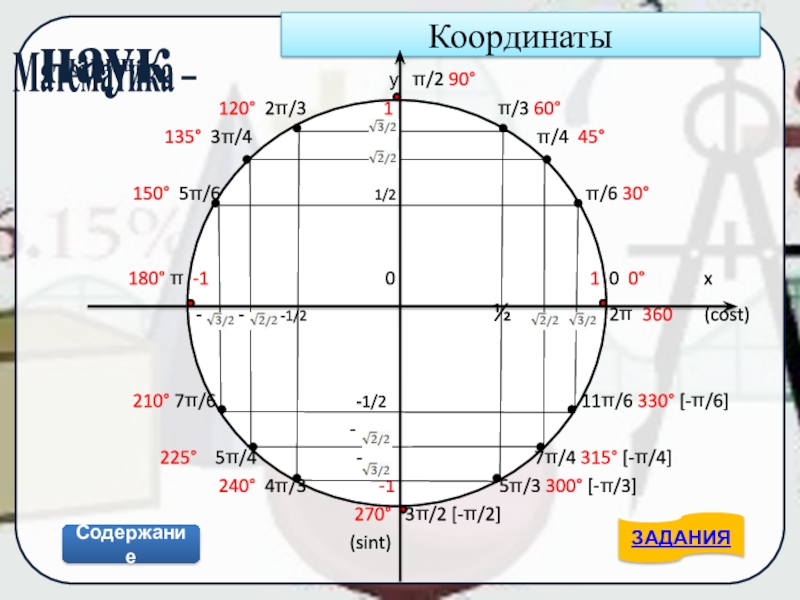
Слайд 15Координаты
у π/2 90°
120° 2π/3 1 π/3 60°
135° 3π/4 π/4 45°
150° 5π/6 1/2 π/6 30°
180° π -1 0 1 0 0° x
- - -1/2 ½ 2π 360 (cost)
210° 7π/6 -1/2 11π/6 330° [-π/6]
-
225° 5π/4 - 7π/4 315° [-π/4]
240° 4π/3 -1 5π/3 300° [-π/3]
270° 3π/2 [-π/2]
(sint)
120° 2π/3 1 π/3 60°
135° 3π/4 π/4 45°
150° 5π/6 1/2 π/6 30°
180° π -1 0 1 0 0° x
- - -1/2 ½ 2π 360 (cost)
210° 7π/6 -1/2 11π/6 330° [-π/6]
-
225° 5π/4 - 7π/4 315° [-π/4]
240° 4π/3 -1 5π/3 300° [-π/3]
270° 3π/2 [-π/2]
(sint)
Содержание
ЗАДАНИЯ
Слайд 17Тригонометрия .
Тригонометрические функции, графики и свойства
y = sinx
y = cosx
y =
tgx
Построение графиков
Слайд 18
у
1
0
-π/2 π/2 π 3π/2 2π 5π/2 3π х
-1
1
0
-π/2 π/2 π 3π/2 2π 5π/2 3π х
-1
-π
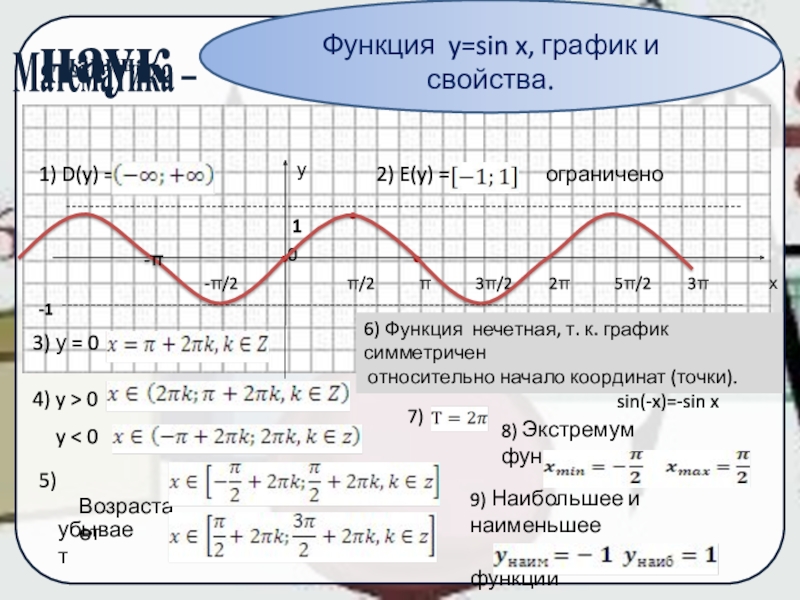
1) D(y) =
2) E(y) = ограничено
3) у = 0
4) y > 0
y < 0
5) Возрастает
убывает
Функция y=sin x, график и свойства.
6) Функция нечетная, т. к. график симметричен
относительно начало координат (точки).
sin(-x)=-sin x
7)
8) Экстремум функции:
9) Наибольшее и наименьшее
значение функции
Слайд 19
у
1
0
-π/2 π/2 π 3π/2 2π 5π/2 3π х
-π -1
1
0
-π/2 π/2 π 3π/2 2π 5π/2 3π х
-π -1
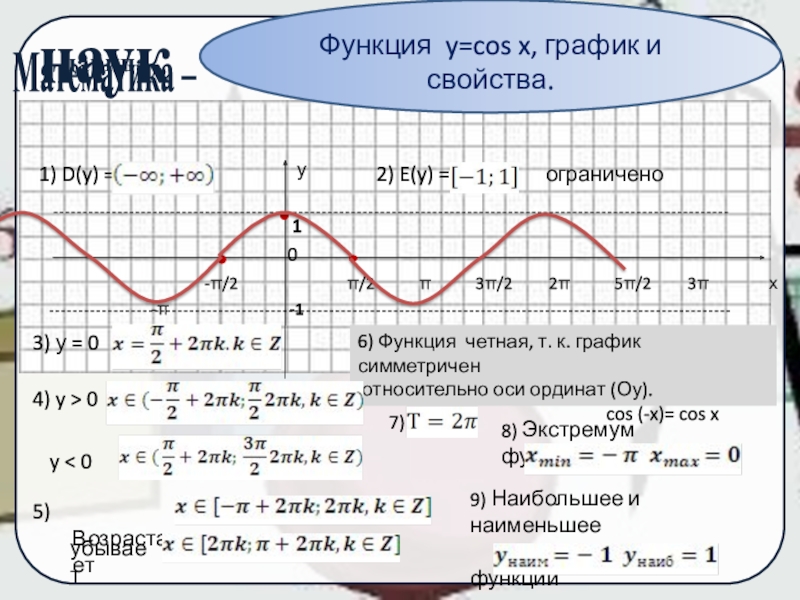
1) D(y) =
2) E(y) = ограничено
3) у = 0
4) y > 0
y < 0
5) Возрастает
убывает
Функция y=cos x, график и свойства.
6) Функция четная, т. к. график симметричен
относительно оси ординат (Оу).
cos (-x)= cos x
7)
8) Экстремум функции:
9) Наибольшее и наименьшее
значение функции
Слайд 20 Функция y = tg x, её свойства и график
1.D(y)=
2.E(y)=
3.tg(-x)=-tgx
4.Возрастает на
5.Периодичная
1
-1
Содержание
Слайд 25Тригонометрия .
Формулы
тригонометрических функций
Формулы
двойного аргумента
Преобразование сумм
тригонометрических функций
в произведение
Формулы
сложения
Видео
«Обзор тождеств»
ЗАДАНИЯ 1 2 3
Содержание
Слайд 26Формулы двойного аргумента
1.sin2x = 2 sinx·cosx;
2.cos2x = cos²x - sin²x;
5. ;
3.cos2x = 1 – 2sin²x;
6.
4.cos2x = 2cos²x-1;
3.cos2x = 1 – 2sin²x;
6.
4.cos2x = 2cos²x-1;
ЗАДАНИЯ
Формулы
Слайд 28Формулы сложения
1.sin(x + y)=
sinx·cosy + siny·cosx
2.cos(x + y)= cosx·cosy - sinx·siny
3.sin(x – y)= sinx·cosy - siny·cosx
4.cos(x – y)= cosx·cosy + sinx·siny
5.
6.
2.cos(x + y)= cosx·cosy - sinx·siny
3.sin(x – y)= sinx·cosy - siny·cosx
4.cos(x – y)= cosx·cosy + sinx·siny
5.
6.
ЗАДАНИЯ
Формулы
Слайд 38Литература
А. Е. Абылкасимов, А. М. Абрамов «Алгебра и начала анализа 10»:
учебник для 10 класса естественно – математического направления общеобразовательных школ – Алматы: Издательство «Мектеп», 2006 – 96с.
А. Е. Абылкасимов, А. М. Абрамов методическое пособие «Алгебра и начала анализа 10»: учебник для 10 класса естественно – математического направления общеобразовательных школ – Алматы: Издательство «Мектеп», 2006.
А. Н. Колмогоров и др. «Алгебра и начала анализа 10 - : Учеб. для общеобразовательных учреждений. – Москва, Просвещение, 1991.
А. Г. Мордкович, В. И. Глизбург «Полный справочник по математике», Москва 2009.
Национальный центр тестирования РК, учебно – методическое пособие, Астана 2011, 2013.
http://window.edu.ru/catalog/resources?p_page=32&p_nr=50
http:// festival.1september.ru
http://yutube.com
А. Е. Абылкасимов, А. М. Абрамов методическое пособие «Алгебра и начала анализа 10»: учебник для 10 класса естественно – математического направления общеобразовательных школ – Алматы: Издательство «Мектеп», 2006.
А. Н. Колмогоров и др. «Алгебра и начала анализа 10 - : Учеб. для общеобразовательных учреждений. – Москва, Просвещение, 1991.
А. Г. Мордкович, В. И. Глизбург «Полный справочник по математике», Москва 2009.
Национальный центр тестирования РК, учебно – методическое пособие, Астана 2011, 2013.
http://window.edu.ru/catalog/resources?p_page=32&p_nr=50
http:// festival.1september.ru
http://yutube.com
