- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему экстремумы функций
Содержание
- 1. экстремумы функций
- 2. 6х - 4cоs x + sin x2e2x – 6 ex-3 x2 + 6 x + 9
- 3. Постройте график функции : у =
- 4. Сформулируйте гипотезу.
- 5. Постройте график функции : у = -
- 6. Постройте график функции : у = -
- 7. Пьер Ферма (1601-1665) — французский математик, один из
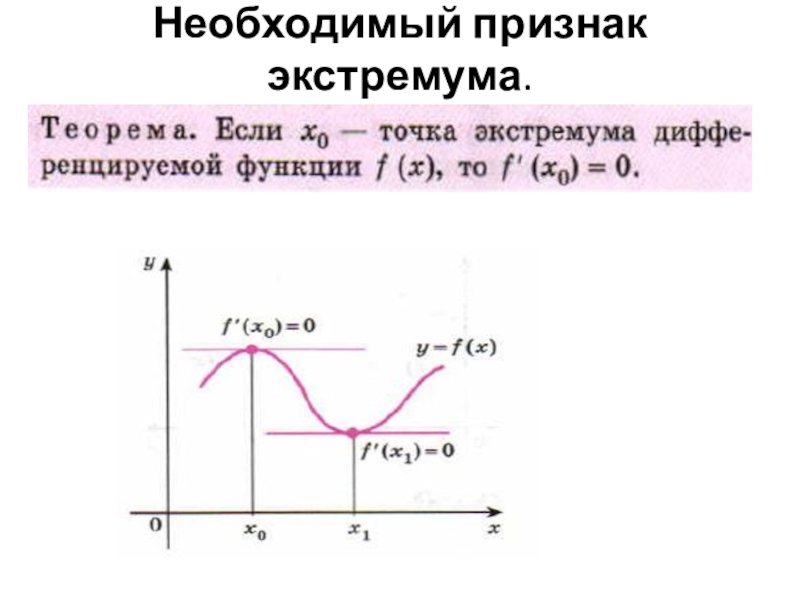
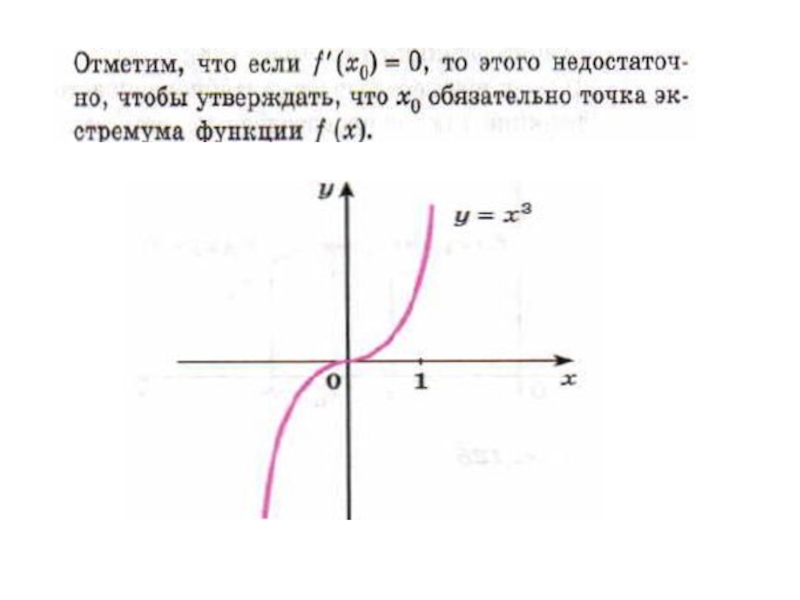
- 8. Необходимый признак экстремума.
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Алгоритм нахождения точек экстремума функции1. Найти область
- 13. д/з: п. 50, № 912 (
- 14. Я умею …Я знаю …Хотелось бы лучше
- 15. Конфуций, Кун-цзы (родился приблизительно 551 - умер
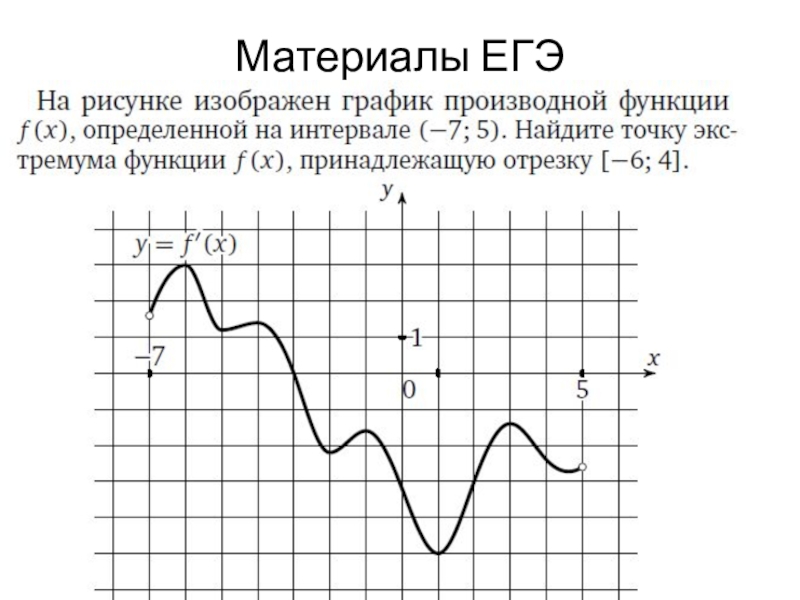
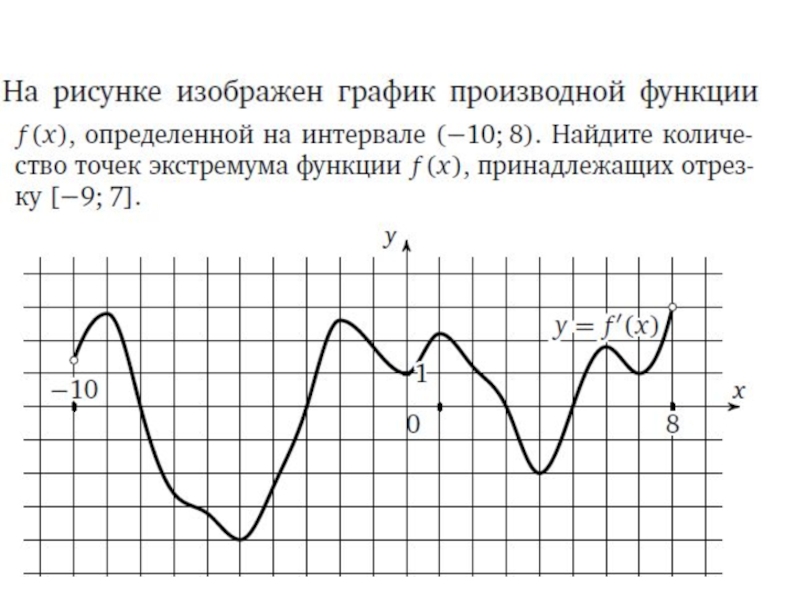
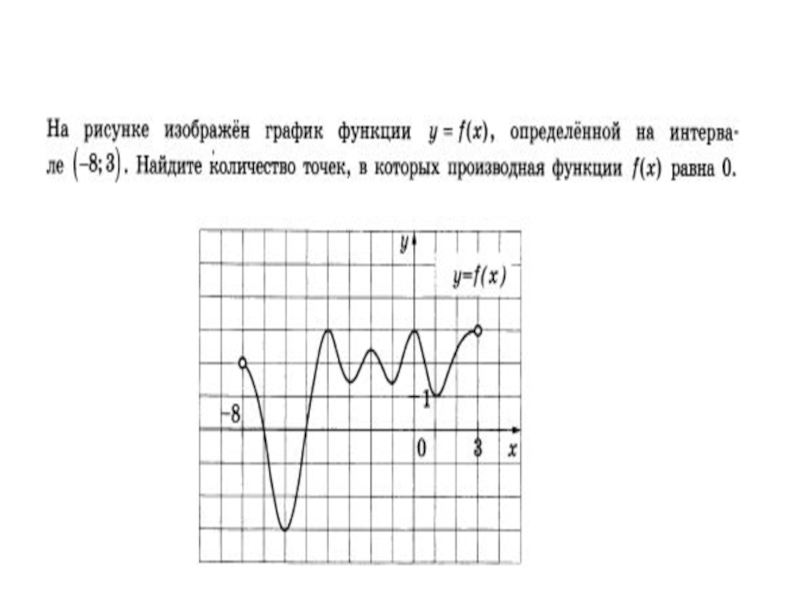
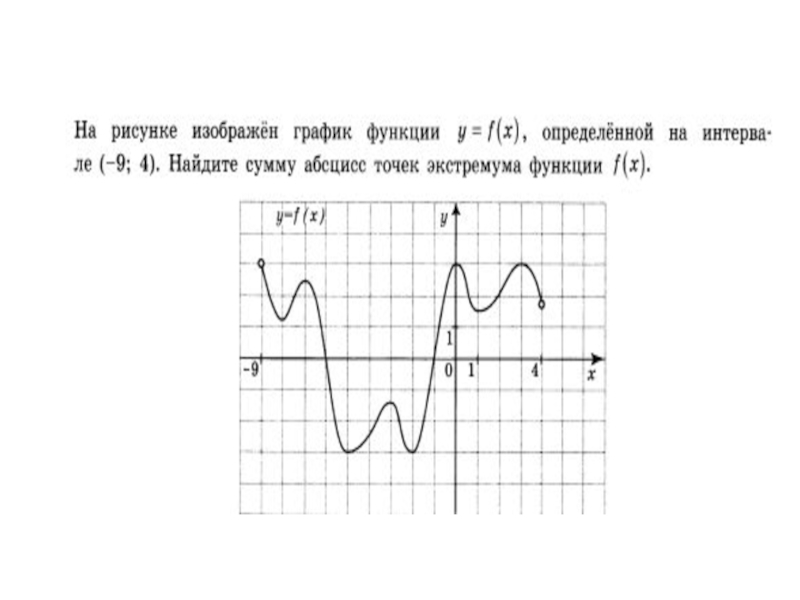
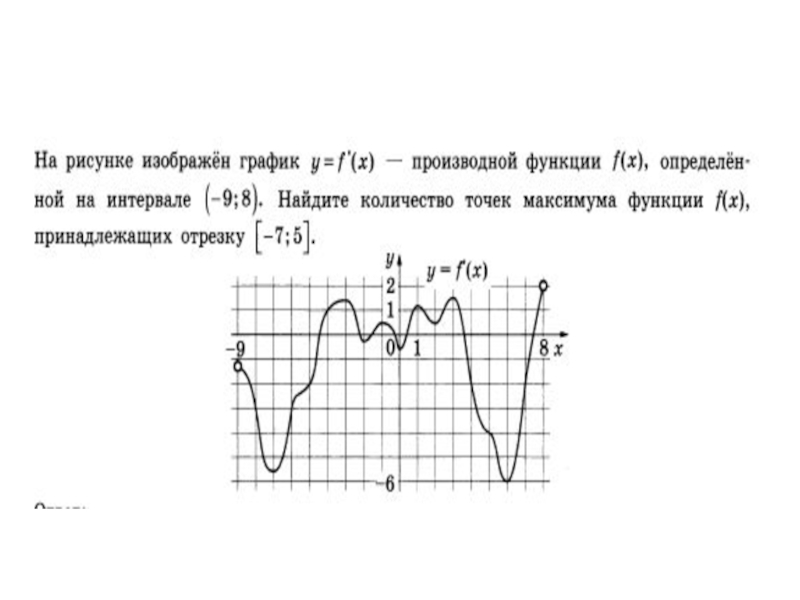
- 16. Материалы ЕГЭ
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
Слайд 1Скажи мне, и я забуду. Покажи мне, и я запомню. Вовлеки меня, и
Китайская мудрость.
Слайд 3Постройте график функции : у = х2 –6х + 8;
Ответьте на вопросы :
Назовите промежутки возрастания и убывания полученного графика.
Назовите точку минимума функции.
Как ведет себя производная вблизи окрестности этой точки, при переходе через эту точку? А в самой этой точке?
Слайд 5Постройте график функции : у = - х2 + 4х –
Ответьте на вопросы :
Назовите промежутки возрастания и убывания полученного графика.
Назовите точку максимума функции.
Как ведет себя производная вблизи этой точки, при переходе через эту точку? А в самой этой точке?
Слайд 6Постройте график функции : у = - х2 + 4х –
Ответьте на вопросы :
Назовите промежутки возрастания и убывания полученного графика.
Назовите точку максимума функции.
Как ведет себя производная вблизи окрестности этой точки, при переходе через эту точку? А в самой этой точке?
Слайд 7Пьер Ферма (1601-1665) — французский математик, один из создателей аналитической геометрии и
Пьер Ферма открыл методы нахождения экстремумов и касательных, которые, с современной точки зрения, сводятся к отысканию производной.
Слайд 12Алгоритм нахождения точек экстремума функции
1. Найти область определения функции.
2. Найти f'(x).
3.
4. Расположить область определения и эти точки на координатной прямой.
5. Определить знаки производной на каждом из интервалов
6. Применить признаки.
7. Записать ответ.
Слайд 14Я умею …
Я знаю …
Хотелось бы лучше научиться …
Мне нравится …
Мне
На уроке я чувствовала себя …
С домашней работой я …
Слайд 15Конфуций, Кун-цзы (родился приблизительно 551 - умер 479 до н. э.),
Великий философ Конфуций однажды сказал: “Три пути ведут к знанию: путь размышления - это путь самый благородный, путь подражания - это путь самый легкий и путь опыта - это путь самый горький”. Выполняя домашнее задание, каждый из вас пройдёт свой путь к знанию.