- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Детская работа по математике на тему Шар.Сфера Криводуд Наталья
Содержание
- 1. Детская работа по математике на тему Шар.Сфера Криводуд Наталья
- 2. Шар - тело, которое состоит из всех
- 3. Сечение шара плоскостью, проходящей через центр шара,
- 4. Сфера – это тело вращения, которое напоминает
- 5. Тогда, сфера – это множество всех точек
- 6. Форма земли
- 7. Рассмотрим полуокружность ACB с центром O и
- 8. Аналогично, если вращать не полуокружность, а полукруг, получим шарПолукруг ABCШар как тело вращения
- 9. Шар и сфера как тела вращения
- 10. Хорда сферы – это отрезок, соединяющий две
- 11. Разветвление: уравнение сферы в координатах в пространстве
- 12. Сфера с центром в точке ОВыведем уравнение
- 13. Пример 1.Пусть дано уравнение: Требуется доказать,
- 14. Площадь сферы
- 15. Формула для нахождения площади сферы выводится аналогично
- 16. Пример 2.Дана сфера, площадь которой равна 64π.
- 17. Во сколько раз изменится площадь поверхности сферы,
- 18. Спасибо за внимание
Слайд 2Шар - тело, которое состоит из всех точек пространства, находящихся на
История возникновения: шаром принято называть тело, ограниченное сферой, т.е. шар и сфера – это разные геометрические тела. Однако оба слова « шар» и « сфера» происходят от одного и того же греческого слова « сфайра» - мяч. При этом слово « шар» образовалось от перехода согласных сф в ш. В XI книге «Начал» Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы. Сфера всегда широко применялось в различных областях науки и техники.
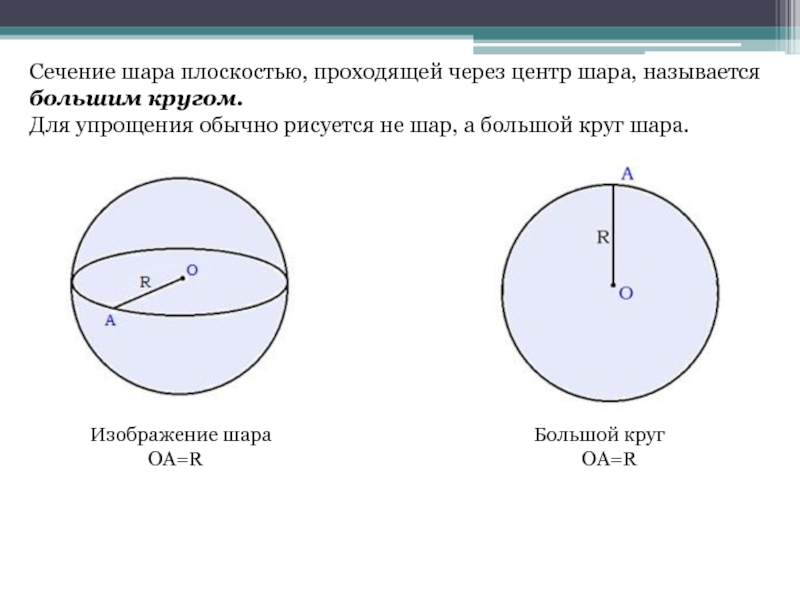
Слайд 3Сечение шара плоскостью, проходящей через центр шара, называется большим кругом.
Для упрощения
Изображение шара
OA=R
Большой круг
OA=R
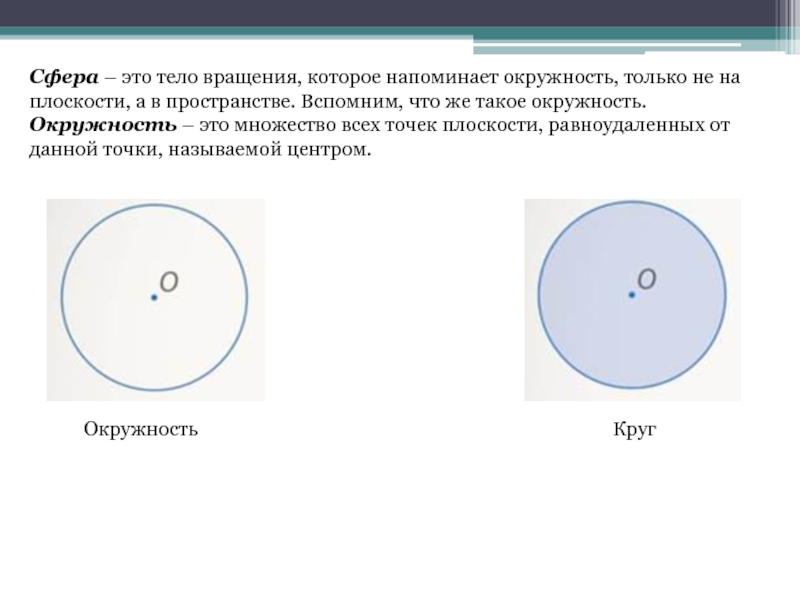
Слайд 4Сфера – это тело вращения, которое напоминает окружность, только не на
Окружность
Круг
Слайд 5Тогда, сфера – это множество всех точек пространства, равноудаленных от данной
Радиус сферы – расстояние, на которое они (точки) удалены от центра. Продолжая аналогию, шар – это круг в пространстве: множество всех точек, заключенных внутри сферы (плюс сама сфера).
Шар – это множество всех точек пространства, расстояние от которых до данной точки, называемой центром, не превосходит радиуса.
Сфера
Шар
Слайд 7Рассмотрим полуокружность ACB с центром O и диаметром AB. Вращая ее
Полуокружность ABC
Сфера как тело вращения
Слайд 8Аналогично, если вращать не полуокружность, а полукруг, получим шар
Полукруг ABC
Шар как
Слайд 10Хорда сферы – это отрезок, соединяющий две точки сферы.
Диаметр сферы –
AF,ED - хорды
CF – диаметр, O – центр
Слайд 12Сфера с центром в точке О
Выведем уравнение сферы радиуса R с
Пусть произвольная точка M (x,y,z) лежит на сфере. Тогда, по определению сферы, OM = R. С другой стороны, расстояние между точками в координатах равно:
Приравнивая это к и возводя в квадрат, приходим к формуле, напоминающей уравнение окружности:
Это и есть уравнение сферы.
Соответственно, шар задается не уравнением, а неравенством:
Слайд 13Пример 1.
Пусть дано уравнение:
Требуется доказать, что данное уравнение задает сферу,
Вспомним общее уравнение сферы:
Наша задача – свести исходное уравнение к уравнению сферы. Для этого выделим полные квадраты:
Таким образом, это действительно сфера, ее центр – точка с координатами , а ее радиус равен
Слайд 15Формула для нахождения площади сферы выводится аналогично формуле для нахождения площади
Аналогично и для сферы. Опишем сферу многогранником и будем увеличивать количество граней до бесконечности. Тогда площадь боковой поверхности многогранника будет стремиться к площади поверхности сферы.
– площадь сферы
Слайд 16Пример 2.
Дана сфера, площадь которой равна 64π. Найти радиус сферы.
Так как
Поделив обе части уравнение на 4π, получим:
Ответ: Радиус сферы равен 4.
Слайд 17Во сколько раз изменится площадь поверхности сферы, если ее радиус увеличили
Так как площадь сферы . Если радиус увеличится в 3 раза, тогда Соответственно, площадь увеличилась в 9 раз:
Замечание: если все измерения фигуры увеличить в X раз, площадь поверхности фигуры вырастет в раз.