- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Числовая окружность
Содержание
- 1. Числовая окружность
- 2. Цель: ввести понятие числовой окружности как модели
- 3. Тема1. Единичная окружностьЕдиничная окружность — окружность, центр которой расположен
- 4. Важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°Угол, который образован положительным
- 5. ЗаданияОбозначьте на единичной окружности угол 225°.1) Определяем, в каком
- 6. Тема 2. Числовая окружность, макеты числовой окружностиЛюбая
- 7. Будем пользоваться единичной окружностью, в которой проведены
- 8. Первый макетКаждая из четырёх четвертей числовой окружности
- 9. Для числовой окружности верно следующее утверждение:если точка M числовой
- 10. Тема 3. Числовая окружность в координатной плоскостиРасположим
- 11. Найдём сначала координаты тех точек координатной плоскости,
- 12. Аналогично можно получить координаты и других точек
- 13. Рассуждаем аналогично для точки M, если теперь она
- 14. Полученные результаты запишем в таблицу
- 15. В какой координатной четверти находится угол 193°, 57°,
- 16. 5. С какой из отмеченных на числовой окружности точек совпадает:12345
- 17. ВыводРассмотрели числовую окружность, её особенности. Каждому действительному
Слайд 2Цель: ввести понятие числовой окружности как модели криволинейной системы координат.
Задачи:
формировать
развивать вычислительные навыки, правильную математическую речь, логическое мышление обучающихся;
формировать умение применять изученный теоретический материал при выполнении письменной работы;
прививать самостоятельность, внимание и аккуратность;
воспитывать ответственное отношение к обучению.
Слайд 3Тема1. Единичная окружность
Единичная окружность — окружность, центр которой расположен в начале координат и
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют
числовой окружностью.
О
Каждому действительному числу t соответствует единственная точка М на этой окружности
Слайд 4Важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°
Угол, который образован положительным направлением оси OX и лучом OA, называется углом
Если точка перемещается по часовой стрелке, получаются отрицательные углы
Если точка перемещается против часовой стрелки, получаются положительные углы
А
А
О
О
Слайд 5Задания
Обозначьте на единичной окружности угол 225°.
1) Определяем, в каком квадранте находится угол:
он больше 180° и
2) Вычисляем, на сколько градусов этот угол отличается от угла 180°.
225° =180° + 45°
Обозначьте на единичной окружности угол −120°.
Угол обозначается в отрицательном направлении. Он находится в III квадранте.
Решение:
−120° = −90° + (−30°)
Слайд 6Тема 2. Числовая окружность, макеты числовой окружности
Любая окружность может рассматриваться как
Единичная окружность — это окружность, радиус которой принимается за единицу измерения.
Длина единичной окружности L равна L=2π⋅R=2π⋅1=2π.
Считаем, что R=1.
Если взять π≈3,14, то длина окружности l может быть выражена числом 2π ≈ 2⋅3,14=6,28.
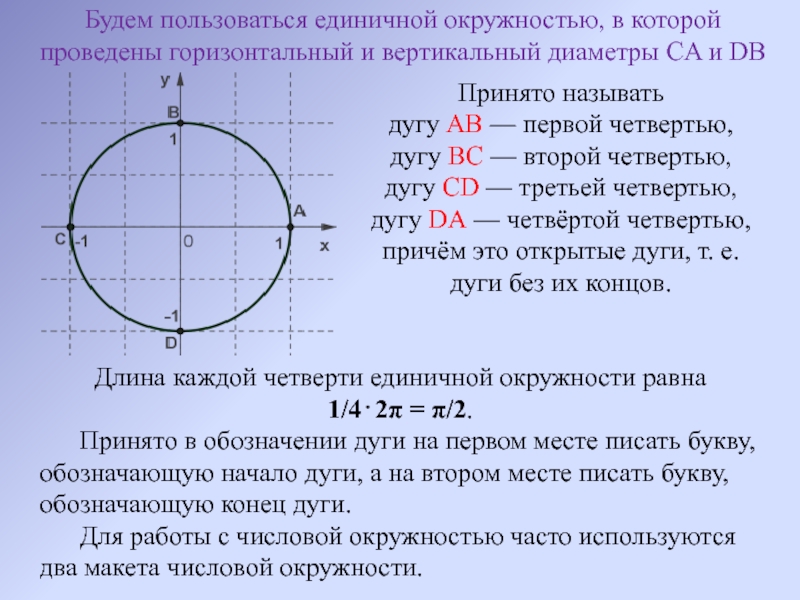
Слайд 7Будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры CA и DB
Принято
дугу AB — первой четвертью, дугу BC — второй четвертью, дугу CD — третьей четвертью, дугу DA — четвёртой четвертью, причём это открытые дуги, т. е. дуги без их концов.
Длина каждой четверти единичной окружности равна
1/4⋅2π = π/2.
Принято в обозначении дуги на первом месте писать букву, обозначающую начало дуги, а на втором месте писать букву, обозначающую конец дуги.
Для работы с числовой окружностью часто используются два макета числовой окружности.
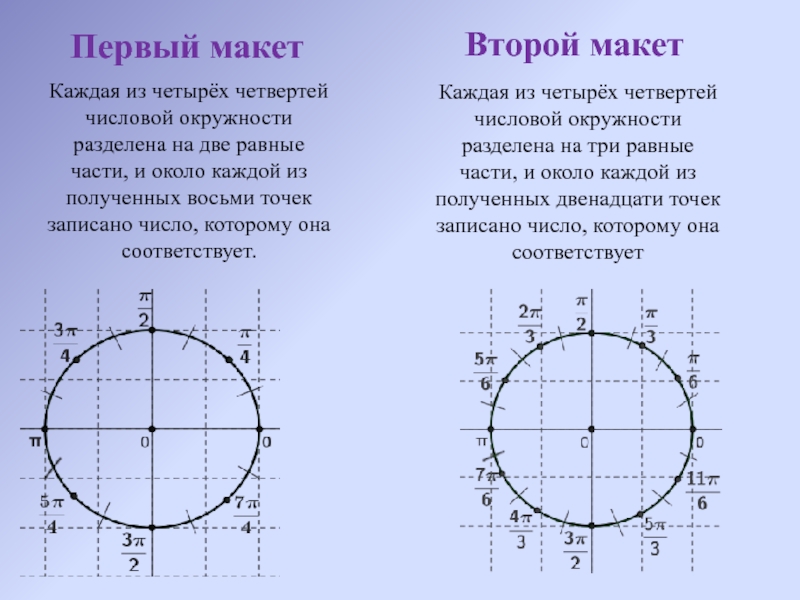
Слайд 8Первый макет
Каждая из четырёх четвертей числовой окружности разделена на две равные
Второй макет
Каждая из четырёх четвертей числовой окружности разделена на три равные части, и около каждой из полученных двенадцати точек записано число, которому она соответствует
Слайд 9Для числовой окружности верно следующее утверждение:
если точка M числовой окружности соответствует числу t, то
На указанных двух макетах написаны числа, соответствующие точкам при первом обходе числовой окружности в положительном направлении, т. е. на промежутке [0;2π].
Таким образом, единичная окружность с установленным соответствием между действительными числами и точками окружности называется числовой окружностью.
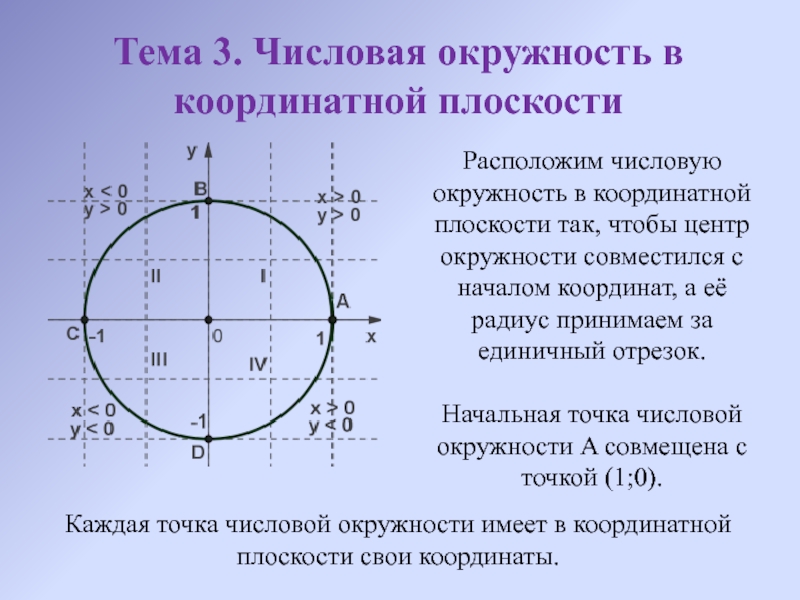
Слайд 10Тема 3. Числовая окружность в координатной плоскости
Расположим числовую окружность в координатной
Начальная точка числовой окружности A совмещена с точкой (1;0).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты.
Слайд 11Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах
Значит, Δ OMP — равнобедренный прямоугольный треугольник и OP=MP, т. е. у точки M абсцисса и ордината равны: x=y
Так как координаты точки M(x;y) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений:
x2+y2=1
x=y
Точка М - середина I четверти.
Опустим перпендикуляр МР на прямую ОА и рассмотрим ∆ОМР.
Так как дуга АМ составляет половину дуги АВ, то ∠МОР=45°
Получили, что координаты точки М, соответствующей числу , будут
М = М
=М
Слайд 12Аналогично можно получить координаты и других точек первого макета числовой окружности,
Полученные результаты запишем в таблицу.
Слайд 13Рассуждаем аналогично для точки M, если теперь она соответствует числу
ΔMOP прямоугольный. Так
Катет MP лежит против угла 30° в прямоугольном треугольнике, значит, равен половине гипотенузы, т. е. ордината точки M равна
MP=1/2; y=1/2
Абсциссу x точки M найдём, решив уравнение:
x2+y2=1;
Получим, что координаты точки M,
соответствующей числу будут М( ) = М
Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.
Слайд 15В какой координатной четверти находится угол 193°, 57°, 281°, 101°?
Определите координаты
Как расположены на числовой окружности точки, соответствующие числам t и π - t ?
Домашнее задание
4. Найдите на числовой окружности точку, которая соответствует: