- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Биквадрат тендеу алгебра (8 класс)
Содержание
- 1. Биквадрат тендеу алгебра (8 класс)
- 2. Сабақтың мақсаты: “Оқушылардың биквадрат теңдеу және квадрат
- 3. “Шатасқан баулар” статегиясы1-топтың тапсырмасы1.ах4+ bх2+с=0 бұл
- 4. 2-топтың тапсырмасы1.Биквадрат теңдеуді шешу үшін, теңдеуді at2+bt+c=0түріндегі
- 5. ах4+вх2+с=0
- 6. Виет теоремасы х2+рх+q=0, а= Х1+ Х2=
- 7. Сәйкестендіру тесті1.a=9, b=17, c=8 коэффициенттері арқылы биквадрат
- 8. Бағалау критериі3.Алмастыру арқылы алғашқы айнымалының мәнін таба
- 9. Үйге тапсырма: №194 (1,2), №198
Сабақтың мақсаты: “Оқушылардың биквадрат теңдеу және квадрат теңдеуге келтірілген теңдеулерді шешуде жаңа айнымалы енгізу әдісімен шешу алгоритмін есептер шығаруда дұрыс қолдана алуға үйрену, өтілген тақырып бойынша білімдерімізді тереңдетіп, жинақтау”.
Слайд 2
Сабақтың мақсаты: “Оқушылардың биквадрат теңдеу және квадрат теңдеуге келтірілген теңдеулерді шешуде
жаңа айнымалы енгізу әдісімен шешу алгоритмін есептер шығаруда дұрыс қолдана алуға үйрену, өтілген тақырып бойынша білімдерімізді тереңдетіп, жинақтау”.
Слайд 3“Шатасқан баулар” статегиясы
1-топтың тапсырмасы
1.ах4+ bх2+с=0 бұл квадрат теңдеу.
2.Квадрат теңдеудің дискрименанты
нөлден үлкен болса екі түбірі бар.
3.5х4-6х2 +1=0 биквадрат теңдеудің коэффициентері a=5, b=-6, c=1.
4.х2-7х+10=0 теңдеуінің түбірлерінің қосындысы х1+х2= 7,
көбейтіндісі х1*х2=-10 тең.
5.ах4+ bх2+с=0, a=0 теңдеуі биквадрат теңдеуі деп аталады.
Мұндағы a, b, c белгілі тұрақты сандар ал х ізделінетің белгісіз.
Бұндай теңдеуді шешу үшін х2=t алмастыруын еңгіземіз.
3.5х4-6х2 +1=0 биквадрат теңдеудің коэффициентері a=5, b=-6, c=1.
4.х2-7х+10=0 теңдеуінің түбірлерінің қосындысы х1+х2= 7,
көбейтіндісі х1*х2=-10 тең.
5.ах4+ bх2+с=0, a=0 теңдеуі биквадрат теңдеуі деп аталады.
Мұндағы a, b, c белгілі тұрақты сандар ал х ізделінетің белгісіз.
Бұндай теңдеуді шешу үшін х2=t алмастыруын еңгіземіз.
Слайд 42-топтың тапсырмасы
1.Биквадрат теңдеуді шешу үшін, теңдеуді at2+bt+c=0
түріндегі квадрат теңдеумен алмастырамыз.Квадрат теңдеуді
шешіп t-ның мәнін t>0 салыстырып, биквадрат теңдеуінің
түбірлерін х2=t1 , х2=t2 теңдеуін шешу арқылы анықтаймыз.
2.х2+3х4-4=0 бұл квадрат теңдеу,коэффициенттері a=1, b=3, c=-4.
3.Биквадрат теңдеудің түбірлерінің ең көп шешімі екеу.
4.Келтірілген квадрат теңдеудің түбірлердің қосындысы
қарама-қарсы алынған екінші коэффициентке,
көбейтіндісі бос мүшеге тең. x1 +x2 =-р, x1 x2= -q
5.х4-20х2+64=0, х2=t, t2-20t+64=0, D=102-64=36,
t= 10±6, t2=16 , t2=4, Жауабы:16; 4
Слайд 5
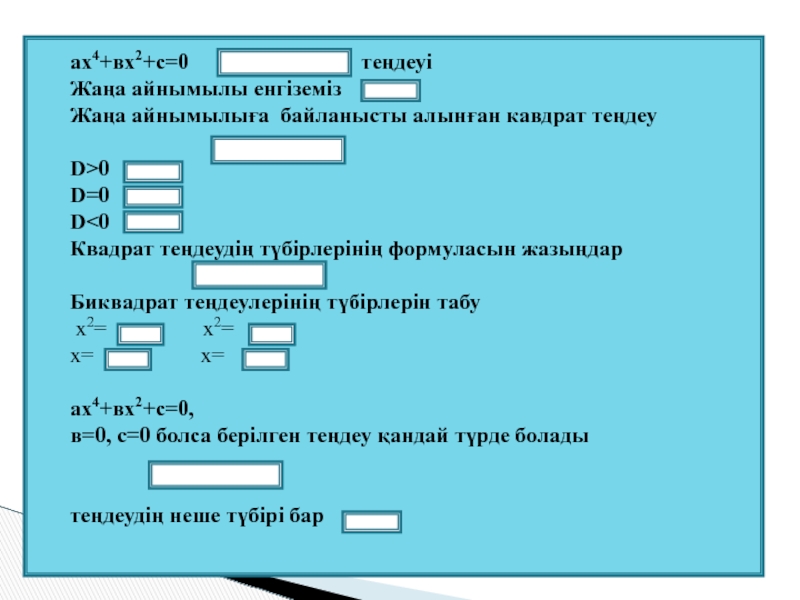
ах4+вх2+с=0
теңдеуі
Жаңа айнымылы енгіземіз
Жаңа айнымылыға байланысты алынған кавдрат теңдеу
D>0
D=0
D<0
Квадрат теңдеудің түбірлерінің формуласын жазыңдар
Биквадрат теңдеулерінің түбірлерін табу
х2= х2=
х= х=
ах4+вх2+с=0,
в=0, с=0 болса берілген теңдеу қандай түрде болады
теңдеудің неше түбірі бар
Жаңа айнымылы енгіземіз
Жаңа айнымылыға байланысты алынған кавдрат теңдеу
D>0
D=0
D<0
Квадрат теңдеудің түбірлерінің формуласын жазыңдар
Биквадрат теңдеулерінің түбірлерін табу
х2= х2=
х= х=
ах4+вх2+с=0,
в=0, с=0 болса берілген теңдеу қандай түрде болады
теңдеудің неше түбірі бар
Слайд 7Сәйкестендіру тесті
1.a=9, b=17, c=8 коэффициенттері арқылы биквадрат теңдеуді табыңдар;
2.х2-8х+9=0 теңдеуінің түбірлерінің
қосындысы мен көбейтіндісі неге тең?
3.х2=0,49 теңдеуінің түбірлері табыңдар;
4.толымсыз квадрат теңдеуді табыңдар ;
5.х1=9, х2= -1 түбірлері арқылы квадрат теңдеу құрыңдар.
3.х2=0,49 теңдеуінің түбірлері табыңдар;
4.толымсыз квадрат теңдеуді табыңдар ;
5.х1=9, х2= -1 түбірлері арқылы квадрат теңдеу құрыңдар.
Жауаптары:
1.а)х1+х2=8; х1*х2=-9;
б) х1+х2=8; х1*х2=9.
2.9х4+17х2+8=0
3.а)х3+х2+12х=0;
б) 49-25х2=0 .
4.а) х2-8х+9=0;
б) х2+8х+9=0.
5.х=±0,7
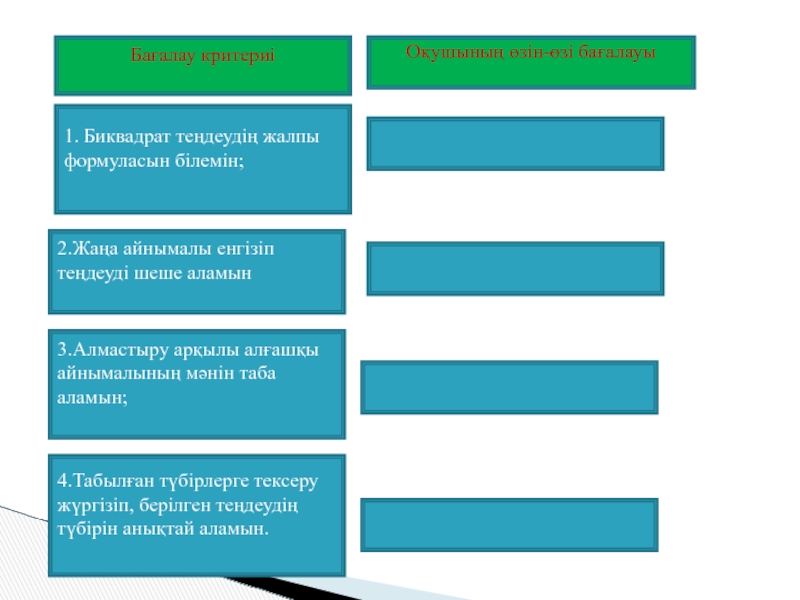
Слайд 8Бағалау критериі
3.Алмастыру арқылы алғашқы айнымалының мәнін таба аламын;
2.Жаңа айнымалы енгізіп теңдеуді
шеше аламын
1. Биквадрат теңдеудің жалпы формуласын білемін;
Оқушының өзін-өзі бағалауы
4.Табылған түбірлерге тексеру жүргізіп, берілген теңдеудің түбірін анықтай аламын.