- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему База задачек для урока по теории вероятности (255 слайдов)
Содержание
- 1. База задачек для урока по теории вероятности (255 слайдов)
- 2. Задача 1.Изготовили 100 деталей, из которых 97
- 3. Решение.Если взять 1 деталь, то событие А
- 4. Задача 2.Бросают игральную кость. Найти вероятность того,
- 5. Решение.а) На гранях игральной кости имеется три
- 6. Задача 3.Даны 5 точек, никакие 3 из
- 7. Решение.Пусть событие А – выбор исходной прямой.
- 8. Задача 4.Набирая номер телефона, абонент забыл две
- 9. Решение.Пусть С – событие, состоящее в том,
- 10. Задача 5.Буквы а, а, в, к, к,
- 11. Событие А – такое расположение карточек с
- 12. Задача 6.Набирая номер телефона, абонент забыл одну
- 13. Пусть В – событие, состоящее в том,
- 14. Задача 7.В ящик, имеющий два отделения, брошено
- 15. Можно выделить всего 4 равновозможных, единственно возможных
- 16. Задача 8.Декан факультета вызвал через старосту трех
- 17. Число равновозможных, единственно возможных и несовместимых случаев
- 18. Задача 9.В библиотечке 25 книг. Наудачу выбирается
- 19. Всего равновозможных, единственно возможных и несовместимых случаев
- 20. Задача 10.Известно, что 5% всех мужчин и
- 21. Пусть мужчин и женщин будет одинаковое (согласно
- 22. Задача 11.Проверено 100 деталей. Среди них оказалось 80 стандартных. Какова относительная частота появления стандартной детали?
- 23. Решение.Пусть событие А – при проверке деталь
- 24. Задача 12.Естествоиспытатель К.Пирсон подбрасывал монету и записывал
- 25. Решение.Относительная частота выпадения гербаW(A) = 12012 =
- 26. Задача 13.Отдел технического контроля обнаружил 5 бракованных
- 27. Ответ: 0,05.
- 28. Задача 14.По цели произведено 20 выстрелов,причем зарегистрировано 18 попаданий.Найти относительную частоту попаданий в цель.
- 29. Ответ:0,9.
- 30. Задача 15.При испытании партии приборов относительная частота
- 31. Ответ: 180.
- 32. Задача 16.На отрезок ОА длины ℓ числовой
- 33. Решение.Разобьем отрезок ОА точками М и К
- 34. Задача 17.Если абонент ждет телефонного вызова с
- 35. Решение.Пусть событие D – вызов произошел в
- 36. Задача 18.На листок бумаги в клетку со
- 37. Решение.На рисунке заштрихована область, попадание центра кружка
- 38. Задача 19.В круг, радиус которого равен R,
- 39. Слайд 39
- 40. АСDА1В1С1D1Задача 20.Внутри прямоугольного параллелепипеда, измерения которого равны
- 41. Решение.Пусть событие N – точка оказалась внутри
- 42. Задача 21.Два друга Х и У условились
- 43. Пусть момент прихода друзей Х и У
- 44. Задача 22.Минное заграждение поставлено в одну линию
- 45. Ответ: 0,2.
- 46. Задача 23.Внутрь круга радиусом R наудачу брошена
- 47. Ответ: 2 . π
- 48. Задача 24.В урне 5 белых шаров, 3
- 49. Решение.1 способПусть А – событие, состоящее в
- 50. Задача 25.Имеется 100 лотерейных билетов. Известно, что
- 51. Решение.Пусть А,В,С – события, состоящие в том,
- 52. Задача 26.В коробке 250 лампочек, из них
- 53. Решение.Пусть А – событие, состоящее в том,
- 54. Задача 27.В коробке лежат 30 галстуков, причем
- 55. Решение.Пусть А – событие, состоящее в том,
- 56. Задача 28.Вероятность того, что студент сдаст экзамен
- 57. Слайд 57
- 58. Задача 29.У продавца имеется 10 оранжевых,8 синих,
- 59. Ответ: 23 . 38
- 60. Задача 30.В денежно-вещевой лотерее на каждые 10000
- 61. Слайд 61
- 62. Задача 31.В ящике 10 лампочек по15 Вт,
- 63. Слайд 63
- 64. Задача 32.В первой урне находятся6 черных и
- 65. Пусть А1 – из первой урны извлечен
- 66. Задача 33.Прибор состоит из двух элементов, работающих
- 67. Пусть событие А – выход из строя
- 68. Задача 34.В экзаменационные билеты включенопо 2 теоретических
- 69. Полный ответ на билет состоит из произведения
- 70. Задача 35.В Санкт-Петербург – 16 мест на
- 71. Событие Е – определенные три студента попадут
- 72. Задача 36.Какова вероятность того, что при 10
- 73. Слайд 73
- 74. Задача 37.Найти вероятность того, что при 9 бросаниях монеты «орел» выпадет ровно 4 раза.
- 75. Слайд 75
- 76. Задача 38.За один выстрел стрелок поражает мишень
- 77. Слайд 77
- 78. Задача 39.В следующих испытаниях найдите вероятности «успеха»
- 79. а) 0,75 , 0,25б) 1 , 2
- 80. Задача 40.Напишите формулы, по которым следует находить
- 81. Слайд 81
- 82. Задача 41.Из набора домино случайно вытаскивают одну
- 83. а) 0,4219б) 0,1406в) 0,5781г) 0,0029
- 84. Слайд 84
- 85. Задача1. 30 абитуриентов на 4 вступительных экзаменах
- 86. Слайд 86
- 87. Задача 2.После группировки данных эксперимента получилась таблица
- 88. Ответ:а) 200б) 5г) 1 и 100
- 89. Задача 3.В нашем классе были собраны данные
- 90. Задача 4.Выборка состоит из всех букв, входящих
- 91. Слайд 91
- 92. Задача 5. Постройте график распределения частот и многоугольник частот по результатам письменного экзамена по математике: 6,7,7,8,9,2,10,6,5,6,7,3,7,9,9,2,3,2,6,6,6,7,8,8,2,6,7,9,7,5,9,8,2,6,6,3,7,7,6,6.
- 93. Решение.Дана выборка объема 40. Ее
- 94. 1110 9 8 7 6 5
- 95. Задача 6.Измерили длины слов (количество букв)в приведенном
- 96. Гистограмма распределения кратностейКратность76543210 1 2 3 4
- 97. Задача 7.Алфавит разбит по порядку на три
- 98. Слайд 98
- 99. Задача 8.В вашем классе соберите данныео днях
- 100. Задача 9. 10 девятиклассников получили за тест
- 101. Слайд 101
- 102. Задача 10.У 25 ребят спросили, сколько в
- 103. Ответ:
- 104. Задача 11.Деталь по плану должна весить 431г.Контроль
- 105. Ответ:а) г) 91%
- 106. Задача 12. В таблице приведены данные опроса,
- 107. Решение. Чтобы найти долю многодетных семей, поделим количество многодетных семей на их общее количество:Ответ: 0,14.
- 108. Задача 13. Перед вами итоговая таблица группового
- 109. Решение. Чтобы найти среднее количество голов за
- 110. Задача 14. В таблице указано количество книг,
- 111. Решение. Среднее арифметическоеЧтобы найти медиану, числа нужно
- 112. Задача 15. Ученик засекал в течение недели
- 113. Решение 1. Найдем среднюю продолжительность дороги в
- 114. Решение 2. Найдем ежедневную разность
- 115. Задача 16. В течение четверти
- 116. Решение. Каждую из оценок нужно взять в
- 117. Задача 17.Президент компании получает зарплату 100 000
- 118. Решение. Как и в предыдущей задаче,
- 119. Задача 18.Какое из следующих утверждений неверно:1) если
- 120. Решение. Любой симметричный ряд обладает таким свойством,
- 121. Задача 19.Средний возраст участников школьного хора составляет
- 122. Ответ: невозможно ответить по этим данным. Возможны
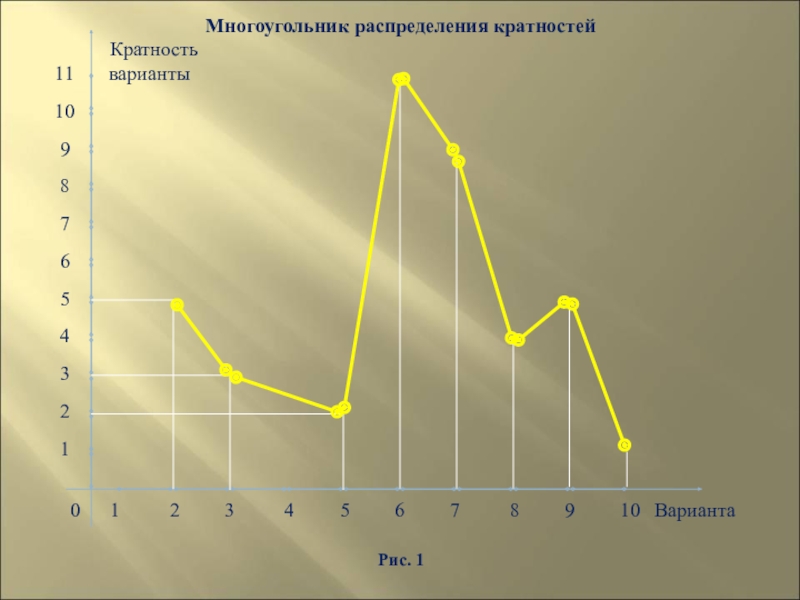
- 123. Многоугольник распределения кратностей
- 124. Многоугольник распределения частот Частота
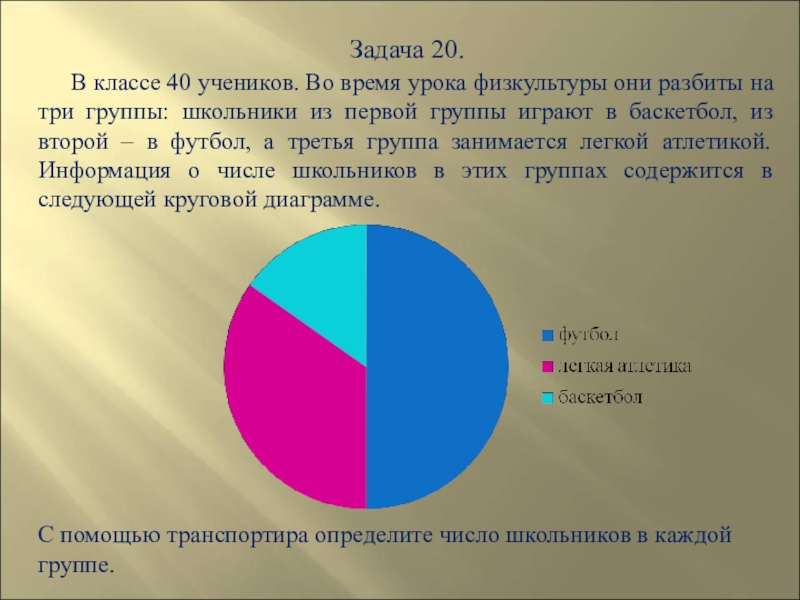
- 125. Задача 20. В классе 40
- 126. Решение. Угол сектора диаграммы, соответствующего второй группе
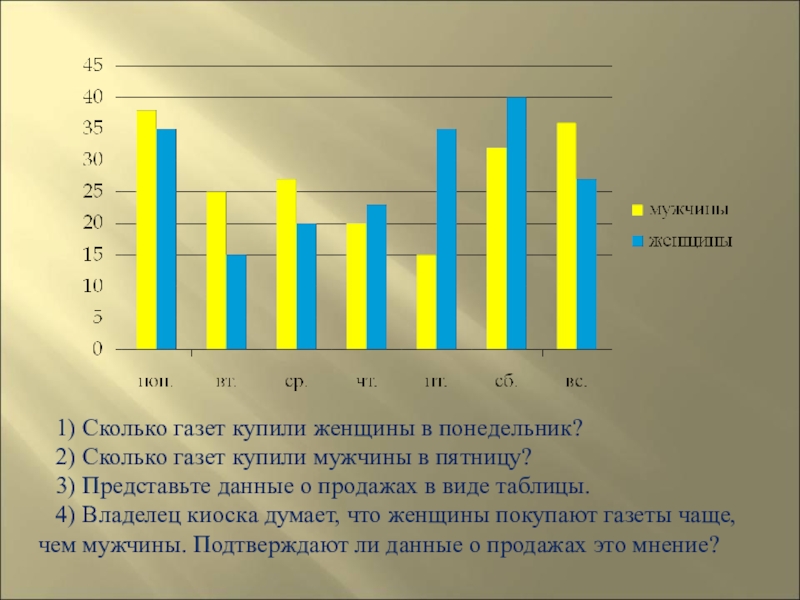
- 127. Задача 21. Владелец газетного киоска
- 128. 1) Сколько газет купили женщины
- 129.
- 130. Задача 22. По заданию учителя
- 131. Решение. Самым холодным было 10
- 132. Задача 23. Контрольную работу по
- 133.
- 134. Поэтому таблица с данными примет следующий вид.
- 135. Задача 24. Среднее арифметическое числового набора равнялась
- 136. Решение. После умножения на 3 все характеристики
- 137. Задача 25.Завод по производству CD-дисков в течение
- 138. Решение. Найдём долю бракованных дисков среди всех
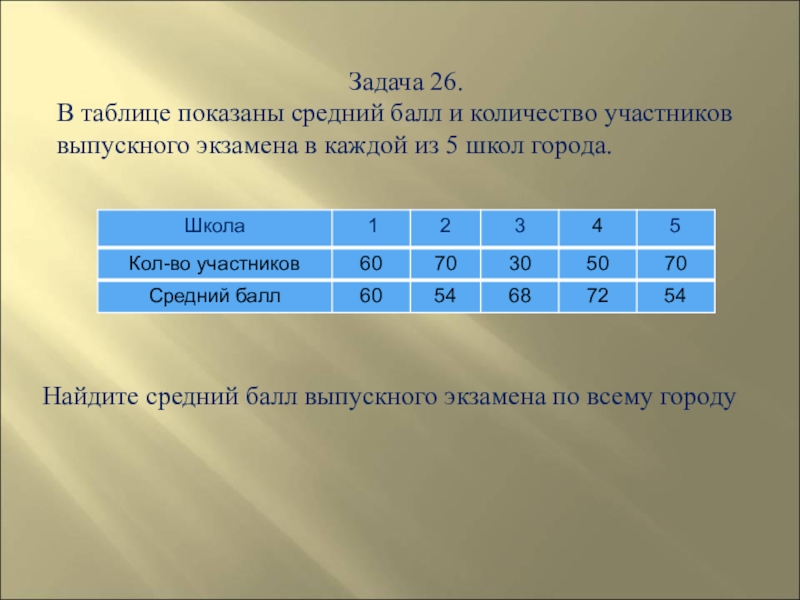
- 139. Задача 26.В таблице показаны средний балл и
- 140. Решение. Что бы найти средний балл по
- 141. Задача 27. Поезда прибывали
- 142. Решение. Исходный набор не совсем числовой: каждый
- 143. Задача 28. Средний возраст 11 игроков
- 144. Решение. Если обозначить через x возраст игрока,
- 145. Задача 29. Числовой набор состоит из всех
- 146. Решение. Данный набор образует арифметическую прогрессию с
- 147. Задача 30. Средний рост в
- 148. Решение. Чтобы показать, что утверждения 1-3 не
- 149. Задача 31. При каких
- 150. а) а≥3. При а
- 151. Задача 32. Три девятых класса писали
- 152. Решение. Объясним ответ для каждого класса. 9
- 153. Задача 33. Из урожая картофеля,
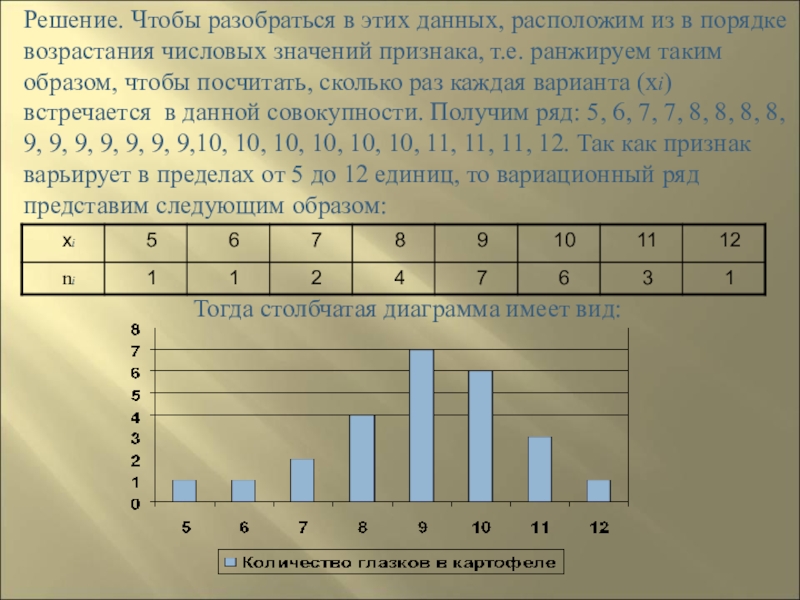
- 154. Решение. Чтобы разобраться в этих данных, расположим
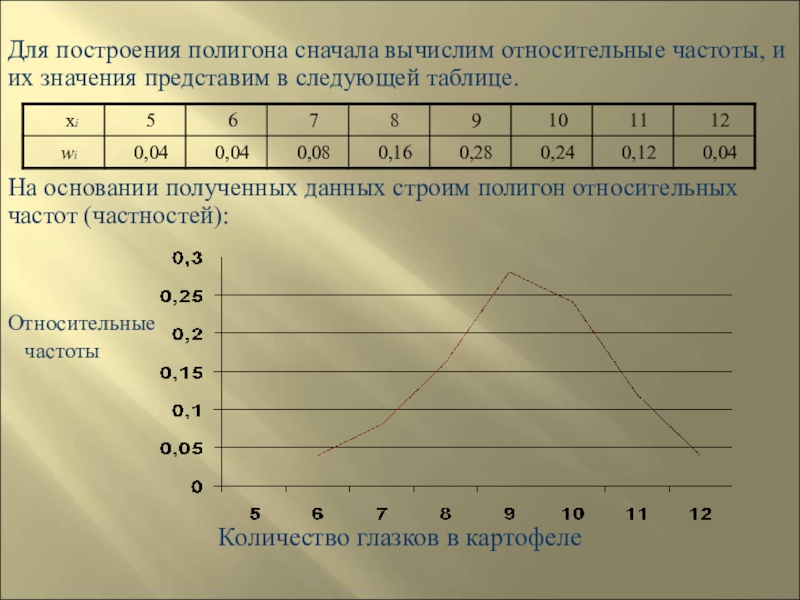
- 155. Для построения полигона сначала вычислим относительные частоты,
- 156. Задача 34. Осуществляя в
- 157. Решение. Для начала проранжируем данный ряд: 2,5;
- 158. Задача 35. Специалист страховой
- 159. Решение. Общая сумма ущерба по пяти страховым
- 160. Задача 36. Торговая компания хочет понять сколько
- 161. 2) Какие покупки, мелкие, средние или крупные,
- 162. Решение.1) Таблица с результатами подсчётов выглядит следующим
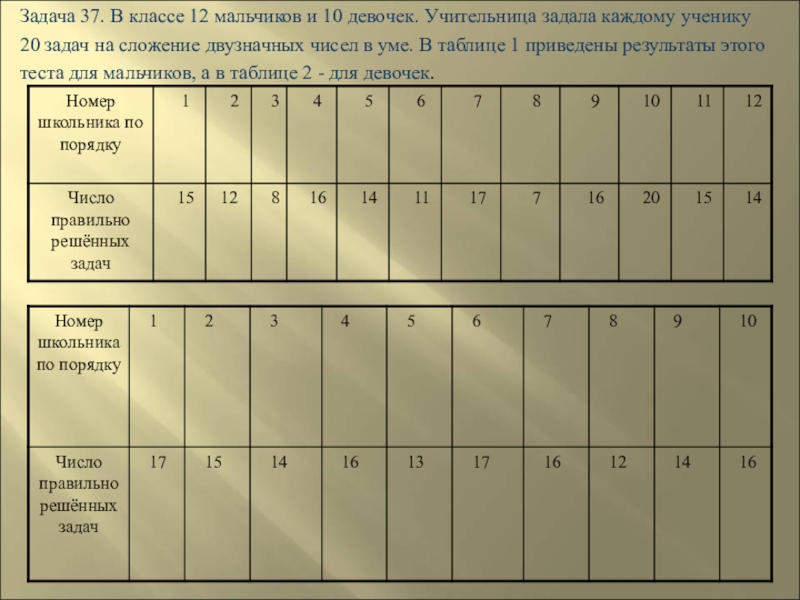
- 163. Задача 37. В классе 12 мальчиков и
- 164. Подсчитайте среднее число
- 165. Среднее число правильно решённых задач одним мальчиком
- 166. Слайд 166
- 167. Задача 1. В первый ящик положили 5
- 168. Слайд 168
- 169. Задача 2. В первом ящике 5 мобильников
- 170. Слайд 170
- 171. Задача 3. Сколько не более чем трехзначных
- 172. Решение.Надо узнать, сколько можно составить однозначных,
- 173. Задача 4.В одной вазе лежит5 яблок,
- 174. а) N = 5+8 = 13 б) N = 5· 8 = 40Ответ:13; 40.
- 175. Задача 5.Ученик должен выполнить практическую работупо математике.Ему
- 176. N = 17+13 = 30 Ответ: 30.
- 177. Задача 6.В танцевальном кружке 5
- 178. N = 5·4 = 20Ответ: 20.
- 179. Задача 7. Имеется 5 билетов денежно-вещевой лотереи,
- 180. Денежно-вещевая лотерея в выборе
- 181. Задача 8.Сколько имеется путей, которыми можно попасть
- 182. N = 2·3 = 6Ответ: 6.
- 183. Задача 9.На книжной полке стоят 25 книг
- 184. N = 25· 15· 10 = 3750Ответ: 3750.
- 185. Задача 10.Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?
- 186. Решение.Составим таблицу: слева от первого столбца –
- 187. Задача 11.Сколько двузначных чисел можно составить, используя цифры 1,4,7, если цифры в числе не повторяются?
- 188. Слайд 188
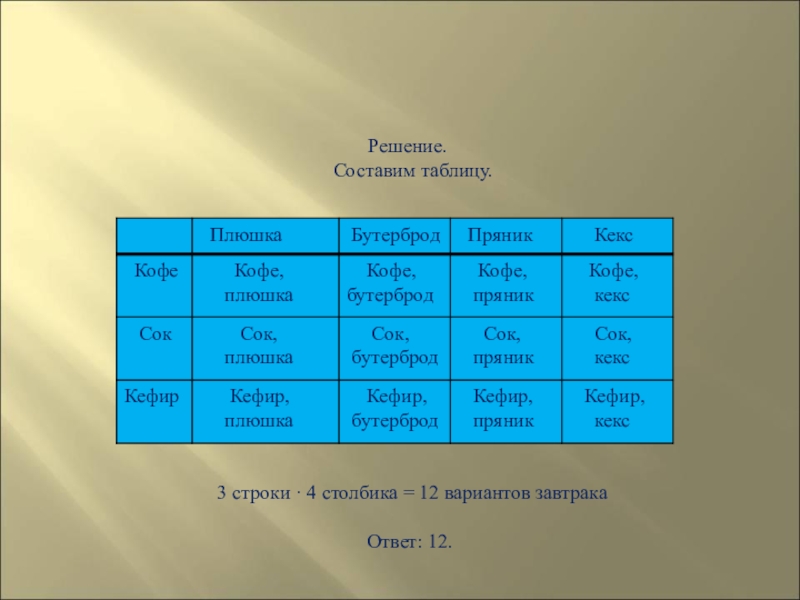
- 189. Задача 12.На завтрак Вова может выбрать плюшку,
- 190. Слайд 190
- 191. Задача13.Сколько двузначных чисел
- 192. Слайд 192
- 193. Задача14.Служитель зоопарка должен дать зайцу 2 различных
- 194. Завтрак зайца1 овощ
- 195. Задача15.Туристическая фирма планирует посещение туристами в Италии
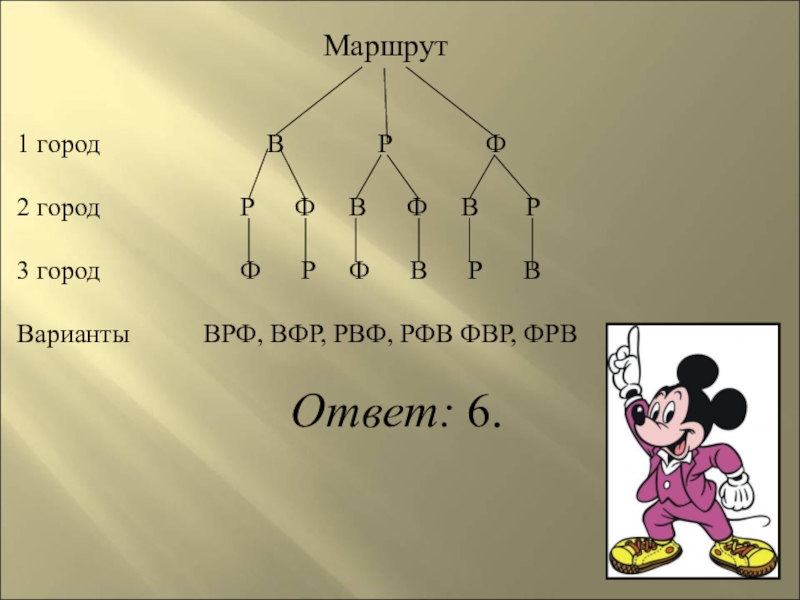
- 196. Маршрут1 город
- 197. Задача16.Несколько стран в качестве символа своего государства
- 198. Ответ: 6.
- 199. Задача17.В коридоре висят три лампочки.Сколько различных способов освещения коридора?
- 200. Слайд 200
- 201. Задача 18.Сколько различных пятизначных чисел можно составить
- 202. Решение.
- 203. Задача19.В соревнованиях участвовало 4 команды. Сколько вариантов распределения мест между ними возможно?
- 204. Р4 = 4! = 1· 2· 3· 4 = 24 Ответ: 24.
- 205. Задача 20.Сколькими способами можно расположить на шахматной
- 206. Р8= 8!=1· 2· 3· 4·
- 207. Задача 21.Сколькими способами можно разместить 12 человек за столом, возле которого поставлены 12 стульев?
- 208. Р12 = 12! = 479001600 Ответ: 479001600.
- 209. Задача 22.Сколькими способами 7 книг разных авторов можно расставить на полке в один ряд?
- 210. Р7 = 7! = 5040 Ответ: 5040.
- 211. Задача 23.Сколько двузначных чисел можно составить из
- 212. Слайд 212
- 213. Задача 24.У нас есть 9 книг из
- 214. Решение.
- 215. Задача 25.Сколько существует вариантов распределения трех призовых мест,если в розыгрыше участвуют7 команд?
- 216. А³7 = 7 ·6 ·5 = 210 Ответ: 210.
- 217. Задача 26.Сколько вариантов расписанияможно составить на один
- 218. А³8 = 8 ·7· 6 = 336 Ответ: 336.
- 219. Задача 27.Сколько вариантов распределения трех путевок в
- 220. А³5 = 5 ·4 ·3 = 60 Ответ: 60.
- 221. Задача 28.В городе проводится первенство по футболу. Сколько в нем состоится матчей, если участвуют 12 команд?
- 222. А²12 = 12· 11 = 132 Ответ: 132.
- 223. Задача 29.Сколько различных музыкальных фразможно составить из 6 нот,если не допускать в одной фразеповторения звуков?
- 224. Слайд 224
- 225. Задача 30.Сколько сигналов можно подать5 различными флажками,поднимая их в любом количествеи в произвольном порядке?
- 226. 1
- 227. Задача 31.В тренировках участвовали 12 баскетболистов.Сколько различных стартовых пятерок может образовать тренер?
- 228. 5С12 = 12!
- 229. Задача 32.Сколькими способами можно заполнить лотерейный билет«5 из 36»?
- 230. 5 С36 =
- 231. Задача 33.Сколькими способами читатель может выбрать 2 книжки из 6 имеющихся?
- 232. 2С6 = 6! =
- 233. Задача 34.Сколькими способами можносоставить дозор из трех
- 234. 3
- 235. Задача 35.Сколькими способами можновыбрать двух человек в президиум,если на собрании присутствует78 человек?
- 236. Слайд 236
- 237. Задача 36.Сколько трехзначных чисел можно составить из цифр 1,2,3,4,5?
- 238. Слайд 238
- 239. Задача 37. В кондитерском магазине продают 4
- 240. Решение.Покупка не зависит от того, в каком
- 241. Задача 38. Сколькими способами можно переставить буквы слова «ананас»?
- 242. Решение.Всего 6 букв. Одинаковые буквыn«а» = 3,
- 243. Задача 39. Семь девушек водят хоровод. Сколькими способами они могут встать в круг?
- 244. Решение.Если бы девушки стояли на месте, то
- 245. Задача 40.Сколко ожерелий можно составить из 7 бусинок?
- 246. Слайд 246
- 247. Задача 41.На сувениры в «Поле Чудес»спонсоры предлагают
- 248. ~
- 249. Задача 42.Сколько перестановок можно сделать из букв слова «Миссисипи»?
- 250. Всего букв в слове 9. Одинаковые
- 251. Задача 43.В книжный магазин поступилироманы Ф.Купера«Прерия», «Зверобой»,
- 252. ~17С5 = (17+5-1)! = 21! =
- 253. Задача 44.Номер автомашины состоит из трех букв русского алфавита и трех цифр.Сколько различных номеров автомашинможно составить?
- 254. Слайд 254
- 255. Используемая литература:1.А.Н.Мордкович,П.В.Семенов.
Слайд 2Задача 1.Изготовили 100 деталей,
из которых 97 стандартных
и 3 бракованных.
Какова вероятность выбора стандартной детали и выбора бракованной детали?
Слайд 3Решение.
Если взять 1 деталь, то событие А – деталь стандартная и
Событие А более возможно, более вероятно,
чем событие В.
Р(А) = 97 , Р(В) = 3
100 100
Ответ: 0,97 ; 0,03.
Слайд 4Задача 2.Бросают игральную кость.
Найти вероятность того, что: а) выпадет четное
Слайд 5Решение.
а) На гранях игральной кости имеется три четные цифры (2,4,6), т.е.
(выпадает любое число очков от 1 до 6).
Значит, Р(А) = 3 = 1
6 2
б) Имеются две цифры, кратные трем (3,6), m = 2, n = 6.
Р(В) = 2 = 1
6 3
в) Искомыми исходами являются цифры 1,2,3,4,6 - всего их пять
m = 5, n = 6.
Р(С) = 5
6
Ответ: Р(А) = 1 ; Р(В) = 1 ; Р(С) = 5 .
2 3 6
Слайд 6Задача 3.Даны 5 точек, никакие
3 из которых не лежат на
Слайд 7Решение.
Пусть событие А – выбор исходной прямой.
Число всех возможных исходов
проходящих через заданные 5 точек.
Т.к. прямая определяется парой точек, и порядок точек внутри этой пары
не имеет значения, то каждая пара должна отличаться хотя бы одной точкой. Следовательно, надо найти число сочетаний из 5 элементов по 2:
²
n = С5 = 5! = 5! = 10
(5-2)!2! 3!2!
Значит, число всех возможных пар 10,
а искомой является только одна пара точек, поэтому
Р(А) = 1
10
Ответ: Р(А) = 1
10
Слайд 8Задача 4.Набирая номер телефона,
абонент забыл две цифры
и набрал их
Определить вероятность того,
что найдены нужные цифры.
Слайд 9Решение.
Пусть С – событие, состоящее в том, что набраны
две нужные
Всех равновозможных, единственно возможных
и несовместимых случаев набора двух цифр из 10 столько,
сколько можно составить
различных размещений из 10 цифр по 2, т.е.
2
А10 = 10·9 = 90
Благоприятствует событию С только один случай из этих 90.
Таким образом, искомая вероятность Р(С) = 1
90
Ответ: Р(С) = 1
90 .
Слайд 10Задача 5.Буквы а, а, в, к, к, о, х написаны
на
Какова вероятность того,
что извлекая все эти карточки
по одной наудачу
(без возвращения обратно), получим в порядке их выхода слово Каховка?
Слайд 11Событие А – такое расположение карточек с названными буквами, при котором
(в порядке их выхода) слово Каховка,
всего равновозможных исходов испытания будет столько, сколько можно сделать перестановок из 7 элементов
n = Р7 = 7! = 5040.
Среди них благоприятными будут те, которые
образуют слово Каховка.
Число их установим так: если бы в этом слове не было повторяющихся букв, то благоприятный исход был бы один. Однако в слове буквы а и к встречаются дважды,
и если их поменяем местами, то снова получим это же слово.
Следовательно, благоприятных исходов окажется не один,
а четыре (m = 4).
Таким образом, вероятность Р(А) = 4 = 1 . 5040 1260
Ответ: Р(А) = 1 .
1260
Слайд 12Задача 6.Набирая номер телефона,
абонент забыл одну цифру
и набрал ее
Найти вероятность того,
что набрана нужная цифра.
Слайд 13Пусть В – событие, состоящее в том,
что набрана нужная цифра.
Диск телефонного аппарата содержит 10 цифр, следовательно, общее число возможных случаев
n = 10.
Эти случаи несовместимы, единственно возможны и равновозможны.
Событию В благоприятствует только один случай. Следовательно, искомая вероятность
Р(В) = 1 = 0,1.
10
Ответ: 0,1.
Слайд 14Задача 7.В ящик, имеющий два отделения, брошено два шарика.
Какова вероятность
что в каждом отделении будет находиться один шарик?
Слайд 15Можно выделить всего 4 равновозможных,
единственно возможных и несовместимых случая:
1) оба
2) оба шарика попали во второе отделение;
3) первый попал в первое отделение,
второй – во второе;
4) первый попал во второе отделение,
второй – в первое.
Из рассмотренных случаев два благоприятствуют попаданию шаров в различные отделения.
Искомая вероятность Р = 2 = 0,5.
4
Ответ: 0,5.
Слайд 16Задача 8.Декан факультета вызвал
через старосту трех студентов
из группы,
состоящую
задания человек.
Староста забыл фамилии
вызванных студентов
и послал наудачу
трех студентов
из указанной группы.
Какова вероятность того,
что к декану явятся
именно вызванные
им студенты?
Слайд 17Число равновозможных, единственно возможных и несовместимых случаев
выбора трех студентов будет
сколько можно составить различных сочетаний из 5 элементов по 3
3
n = С5 = 5·4·3 = 10,
1·2·3
а благоприятствует условию только один (m = 1).
Искомая вероятность Р = 1 = 0,1.
10
Ответ: 0,1.
Слайд 18Задача 9.В библиотечке
25 книг.
Наудачу выбирается 3 книги.
Какова вероятность
что будут выбраны
нужные книги?
Слайд 19Всего равновозможных, единственно возможных и несовместимых случаев
будет столько, сколько можно
3
А25 = 25·24·23
а число случаев, благоприятствующих тому,
что будут выбраны нужные три книги,
столько, сколько можно составить
перестановок из 3 элементов Р3 = 3! = 1·2·3.
Искомая вероятность Р = 1·2·3 = 1
25·24·23 2300
Ответ: 1 .
2300
Слайд 20Задача 10.Известно, что 5%
всех мужчин
и 0,25% всех женщин –
страдает дальтонизмом.
Какова вероятность того,
что это лицо – мужчина
(считать, что мужчин и женщин одинаковое число).
Слайд 21Пусть мужчин и женщин будет одинаковое (согласно условию) произвольное число, например,
Из 10000 мужчин, страдающих дальтонизмом, будет 10000·0,05 = 500,
а женщин 10000·0,0025 = 25.
Таким образом, из 20000 человек 525
(n = 525) страдают дальтонизмом.
Тогда вероятность того, что наудачу выбранное лицо, страдающее дальтонизмом,
мужчина, равна Р = 500 .
525
Ответ: 500 .
525
Слайд 22Задача 11.Проверено 100 деталей.
Среди них оказалось 80 стандартных. Какова относительная
Слайд 23Решение.
Пусть событие А – при проверке деталь
оказалась стандартной.
По определению
появления этого события
W(A) = 80 = 0,8
100
Ответ: 0,8.
Слайд 24Задача 12.Естествоиспытатель К.Пирсон подбрасывал монету
и записывал полученный результат.
Проделав эту
что герб выпадал в 12012 случаях.
Какова относительная частота выпадения герба?
Слайд 26Задача 13.Отдел технического контроля обнаружил
5 бракованных книг
в партии из
отобранных 100 книг.
Найти относительную частоту появления
бракованных книг.
Слайд 28Задача 14.По цели произведено
20 выстрелов,
причем зарегистрировано
18 попаданий.
Найти относительную частоту
Слайд 30Задача 15.При испытании партии приборов
относительная частота
годных приборов 0,9.
Найти число
если всего было проверено
200 приборов.
Слайд 32Задача 16.На отрезок ОА длины ℓ числовой оси Ох наудачу поставлена
Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит
от его расположения на числовой оси.
Слайд 33Решение.
Разобьем отрезок ОА точками М и К на три равные части.
Требование
попадет на отрезок МК длины ℓ .
3
Искомая вероятность Р = ℓ : ℓ = 1 .
3 3
Ответ: 1 .
3
О
М К
А
В(x)
X
Слайд 34Задача 17.Если абонент ждет телефонного вызова с 2 до 3 часов,
то какова вероятность того, что этот вызов пройдет
с 2ч 30мин до 2ч 40мин.?
Слайд 35Решение.
Пусть событие D – вызов произошел в течение
10мин после половины
Изобразим все исходы испытания в виде отрезка ОА
на прямой Ох:
Событие D произойдет, если точка (вызов)
окажется на отрезке СВ.
Следовательно, Р(D) = СВ = 1 .
ОА 6
Ответ: 1 .
6
О С В А
х
Слайд 36Задача 18.На листок бумаги в клетку
со стороной 10мм падает кружок
диаметра 2мм.
Какова вероятность того, что кружок целиком попадет внутрь клетки?
Слайд 37Решение.
На рисунке заштрихована область,
попадание центра кружка в которую
дает возможность
что кружок не заденет ни одной из сторон квадрата.
Эта область представляет собой квадрат
со стороной 8мм.
Искомая вероятность равна
Р(А) = 8·8 = 0,64.
10·10
Ответ: 0,64.
2
8
10
Слайд 38Задача 19.В круг, радиус которого равен R, вписан
правильный треугольник.
Какова вероятность
что на удачу взятая точка круга окажется
внутри треугольника?
А
В
С
к
Слайд 39 Пусть событие D
выбранная точка окажется внутри треугольника.
Так как точка выбирается на удачу, можно допустить,
что все исходы испытания распределены равномерно.
Следовательно, Р(D) = SΔАВС.
Sкруга
Но площадь круга Sкруга = πR²,
а площадь треугольника
SΔАВС = 3√3R² .
4
Отсюда Р(D) = 3√3 R²· πR² ≈ 0,414…
4
Ответ: 0,414.
Слайд 40
А
С
D
А1
В1
С1
D1
Задача 20.Внутри прямоугольного параллелепипеда,
измерения которого равны 4,6,10см,
наудачу выбирается точка
Какова вероятность того,
что она окажется внутри
данного куба,
ребро которого 3см?
В
4
6
10
3
3
к
Слайд 41Решение.
Пусть событие N – точка оказалась внутри куба
с ребром, равным
Будем считать, что исходы испытания
распределены равномерно.
Тогда вероятность наступления события N
пропорциональна мере этого куба и равна
Р(N) = Vкуба
Vпар.
Но объем куба Vкуба = 27см³,
а объем параллелепипеда Vпар. = 240см³.
Следовательно, Р(N) = 27 = 0,1125.
240
Ответ: 0,1125.
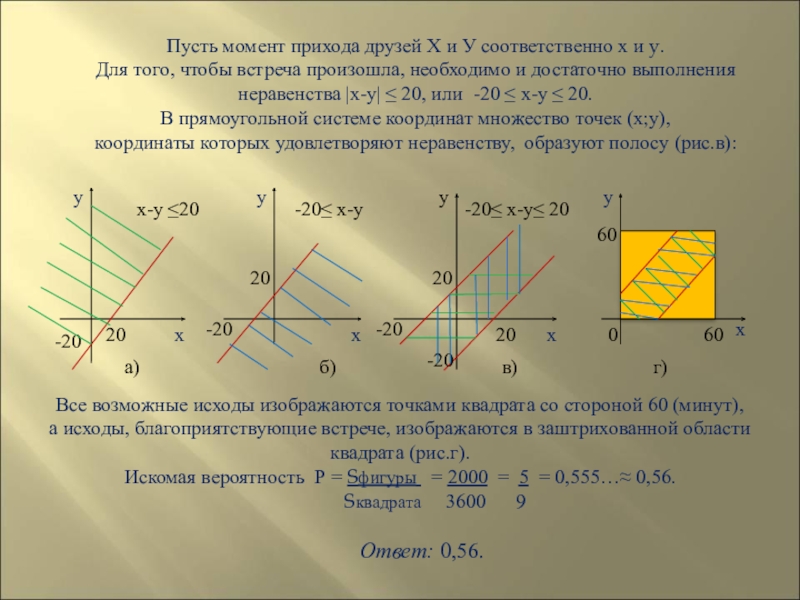
Слайд 42Задача 21.Два друга Х и У условились встретиться в определенном месте
12 и 13 часами,
при этом пришедший первым ждет другого в течение 20 минут, после чего уходит.
Чему равна вероятность встречи друзей Х и У,
если приход каждого из них
в течение указанного часа
может произойти
наудачу и моменты прихода
независимы?
Х
У
Слайд 43Пусть момент прихода друзей Х и У соответственно x и y.
Для
В прямоугольной системе координат множество точек (х;у),
координаты которых удовлетворяют неравенству, образуют полосу (рис.в):
у
у
у
у
х
х
х
х
20
-20
20
-20
20
20
-20
-20
0
60
60
х-у ≤20
-20≤ х-у
а)
б)
в)
г)
Все возможные исходы изображаются точками квадрата со стороной 60 (минут),
а исходы, благоприятствующие встрече, изображаются в заштрихованной области квадрата (рис.г).
Искомая вероятность Р = Sфигуры = 2000 = 5 = 0,555…≈ 0,56.
Sквадрата 3600 9
Ответ: 0,56.
-20≤ х-у≤ 20
Слайд 44Задача 22.Минное заграждение
поставлено в одну линию
с интервалами между минами
Какова вероятность того,
что корабль шириной 20м, пересекая это заграждение
под прямым углом,
подорвется на мине?
(Размерами мин можно пренебречь).
Слайд 46Задача 23.Внутрь круга радиусом R наудачу брошена точка.
Найти вероятность того,
окажется внутри
вписанного
в круг квадрата.
к
Слайд 48Задача 24.В урне 5 белых шаров,
3 черных, 2 в полоску
Найти вероятность того, что из урны будет извлечен одноцветный шар.
Слайд 49Решение.
1 способ
Пусть А – событие, состоящее в извлечении белого шара;
В
Т.к. событию А+В благоприятствует 8 исходов,
а число всех шаров в урне 17, то
Р(А+В) = 8
17
2 способ
Р(А) = 5 , Р(В) = 3 , значит, Р(А)+Р(В) = 8
17 17 17
Ответ: 8 .
17
Слайд 50Задача 25.Имеется 100 лотерейных билетов.
Известно, что на 5 билетов попадает
по 20 руб., на 10 – по 15 руб., на 15 – по 10 руб.,
на 25 – по 2 руб. и на остальные – ничего.
Найти вероятность того, что на купленный билет будет получен выигрыш не меньше 10 руб.
Слайд 51Решение.
Пусть А,В,С – события, состоящие в том,
что на купленный билет
Т.к. события А,В и С несовместны, то
Р(А+В+С) = Р(А)+Р(В)+Р(С) = 5 + 10 + 15 = 0,3
100 100 100
Ответ: 0,3.
Слайд 52Задача 26.В коробке 250 лампочек, из них
100 по 100 Вт,
50 - по 15 Вт.
Вычислить вероятность того, что мощность любой взятой наугад лампочки
не превысит 60 Вт.
Слайд 53Решение.
Пусть А – событие, состоящее в том, что мощность лампочки
равна
достоверное событие, т.е. Р(А)+Р(В)+Р(С)+Р(D) = 1.
События «мощность лампочки не более 60 Вт»
и «мощность лампочки более 60 Вт» – противоположные.
По свойству противоположных событий
Р(А)+Р(В)+Р(С) = 1- Р(D),
Р(А+В+С) = 1- 100 = 150 = 3
250 250 5
Ответ: 3 .
5
Слайд 54Задача 27.В коробке лежат 30 галстуков, причем 12 из них красные,
Определить вероятность того, что
из 4 наудачу вынутых галстуков все они окажутся одного цвета.
Слайд 55Решение.
Пусть А – событие, состоящее в том, что все 4 галстука
В – все 4 галстука будут белые.
4 галстука из 30 красных можно выбрать
4 4
С30 способами, а из 12 - можно выбрать С12 способами.
Поэтому вероятность того, что все 4 галстука будут красные, равна
4 4
Р(А) = С12 = 11 , аналогично белые Р(В) = С18 = 68 .
4 609 4 609
С30 С30
Т.к все 4 галстука должны быть одного цвета, то искомая вероятность
Р = Р(А)+Р(В) = 11 + 68 = 79 = 0,13 .
609 609 609
Ответ: 0,13.
Слайд 56Задача 28.Вероятность того, что студент сдаст экзамен на отлично,
равна 0,2;
на удовлетворительно – 0,3;
на неудовлетворительно – 0,1. Определить вероятность того,
что студент сдаст экзамен.
Слайд 57
Р(А+В+С) = Р(А)+Р(В)+Р(С) = 0,2+0,4+0,3 = 0,9
2 способ.
Сумма вероятностей событий, образующих полную систему, равна 1, тогда
Р(А+В+С) = 1 – Р(D) = 1 - 0,1 = 0,9
Ответ: 0,9.
Слайд 58Задача 29.У продавца имеется
10 оранжевых,8 синих, 5 зеленых
и 15
Вычислите вероятность того,
что купленный шар
окажется оранжевым, синим
или зеленым.
Слайд 60Задача 30.В денежно-вещевой лотерее
на каждые 10000 билетов разыгрывается 150 вещевых
Определить вероятность
выигрыша
денежного или вещевого
на один лотерейный билет.
Слайд 62Задача 31.В ящике 10 лампочек по15 Вт,
10 – по 25
Определить вероятность того, что взятая наугад лампочка имеет мощность более 60 Вт,
если известно,
что число ватт на взятой лампочке – четное.
Слайд 63
Пусть событие А состоит в том, что лампочка имеет мощность более 60 Вт, а событие В – что число ватт является четным. Но «более 60 Вт» – это в данном случае 100 Вт и, значит, Р(АВ) = 25 = 5 ,
60 12
а «четное число ватт» – это 60 и 100 Вт, т.е. Р(В) = 40 = 2
60 3
Искомая вероятность Рв(А) = Р(АВ) = 5 : 2 = 5 .
Р(В) 12 3 8
Ответ: 5 .
8
Слайд 64Задача 32.В первой урне находятся
6 черных и 4 белых шара,
во
Из каждой урны извлекают
по одному шару.
Какова вероятность того,
что оба шара окажутся
белыми?
15
28
Слайд 65Пусть А1 – из первой урны извлечен белый шар;
А2 – из
События А1 и А2 независимы.
Р(А1) = 4 = 2 , Р(А2) = 7
10 5 12
Р(А1·А2) = 2·7 = 7 .
5·12 30
Ответ: 7 .
30
Слайд 66Задача 33.Прибор состоит из двух элементов,
работающих независимо.
Вероятность выхода из строя
Вероятность выхода из строя
второго элемента равна 0,3.
Найти вероятность того, что:
а) оба элемента выйдут
из строя;
б) оба элемента будут
работать.
Слайд 67Пусть событие А – выход из строя первого элемента, событие Е
из строя второго элемента. Эти события независимы ( по условию).
а) одновременно появление А и Е есть событие АЕ
Р(АЕ) = 0,2·0,3 = 0,06
б) если работает первый элемент, то имеет место событие Ā (противоположное событию А – выходу этого элемента из строя);
Если работает второй элемент – событие Ē, противоположное событию Е
Р(Ā) =1- 0,2 = 0,8 и Р(Ē) = 1-0,3 = 0,7
Тогда событие, состоящее в том, что будут работать оба элемента,
есть ĀĒ.
Р(ĀĒ) = Р(Ā)·Р(Ē) = 0,8·0,7 = 0,56.
Ответ: 0,56.
Слайд 68Задача 34.В экзаменационные билеты включено
по 2 теоретических вопроса
и по 1
Всего составлено 28 билетов.
Вычислить вероятность того,
что, вынув наудачу билет,
студент ответит на все вопросы,
если он подготовил
50 теоретических вопросов
и 22 задачи.
Слайд 69Полный ответ на билет состоит из произведения двух событий:
Студент одновременно ответит
и решит задачу (событие В).
Число всех возможных комбинаций из 56 вопросов по 2
2
С56 = 56! = 54!55·56 = 1540
54!·2! 54!·2
Т.к. студент подготовил только 50 вопросов, то число исходов, благоприятствующих событию А, есть
2 2
С50 = 50! = 48!·49·50 = 1225 , Р(А) = С50 = 1225 = 245
48!·2! 48!·2 2 1540 308
С56
Вероятность события В определяется тем, что студент знает 22 задачи из 28 возможных: Р(В) = 22 = 11.
28 14
Т.к. события А и В независимы и должны выполняться одновременно, то Р(АВ) = Р(А)·Р(В) = 245·11 = 0,625.
308·14
Ответ: 0,625.
Слайд 70Задача 35.В Санкт-Петербург – 16 мест на практику,
в Киев –
Какова вероятность того,
что определенные три студента
попадут в один город?
Практика
Слайд 71Событие Е – определенные три студента попадут в один город.
Это событие
или в виде события С1 – указанные 3 студента попадут
в С.- Петербург;
или в виде события С2 – попадут в Киев;
или в виде события С3 – попадут в Баку.
Каждое из этих событий можно рассматривать как совмещение трех событий.
Например, событие С1 – в С.-Петербург попадут и первый из указанных студентов (событие А1), и второй студент
(событие А2), и третий из указанных студентов
(событие А3).
Вероятности этих событий
Р(А1) = 15 , Р(А2) =РА1(Е) = 14 , Р(А1) = РА2(Е) = 13
30 29 28
Аналогично можно рассматривать и события С2 и С3.
По правилам сложения и умножения вероятностей
Р(Е) = 15·14·13 + 10· 9 · 8 + 5 · 4· 3 = 88
30·29·28 30·29·28 30·29·28 609
Ответ: 88 .
609
Слайд 72Задача 36.Какова вероятность того,
что при 10 бросаниях игрального кубика «четверка»
б) ровно 2 раза; в) ровно 6 раз;
г) не выпадет ни разу?
Слайд 73
Число n независимых повторений (бросаний) равно 10.
Число k «успехов» равно 3.
Вероятность p «успеха», т.е.вероятность выпадения «четверки» при одном бросании кубика, равна 1 , а вероятность «неудачи» равна 5 .
6 6
3 3 7
а) Р10(3) = С10 (1)(5) = 120·0,00129 ≈0,155
6 6
2 2 8 6 6 4
б) Р10(2) = С10 (1)(5) в) Р10(6) = С10 (1)(5)
6 6 6 6
0 0 10 10
г) Р10(0) = С10(1)(5) = (5)
6 6 6 Ответ: а) 0,155.
Слайд 75
«Успех» означает выпадение «орла» и его вероятность p = 0,5.
«Неудача» означает выпадение «решки» и ее вероятность q = 0,5.
Бросания предполагаем независимыми друг от друга.
Это частный случай общей схемы Бернулли, в котором
n=9, k = 4, p = 0,5, q = 0,5.
По формуле Бернулли
4 4 9-4 9
Р9(4) = С9(0,5)(0,5) = 9! · (1) = 6·7·8·9 · 1 = 7·2·9 = 63 ≈ 0,246
4!5! 2 1·2·3·4 512 512 256
Ответ: 0,246.
Слайд 76Задача 38.За один выстрел стрелок поражает мишень с вероятностью 0,1.
Найти вероятность
что при 5 выстрелах он хотя бы раз попадет
в мишень.
Слайд 77
Считаем, что все 5 выстрелов производятся независимо друг от друга.
«Успех» означает попадание в мишень при одном выстреле.
Его вероятность p = 0,1.
«Неудача» означает выстрел мимо мишени.
Ее вероятность равна q = 1-0,1 = 0,9.
Число k «успехов» отлично от нуля: kЄ {1,2,3,4,5},
n =5, p = 0,1, q = 0,9.
А – событие, заключающееся в том, что при 5 выстрелах
будет хотя бы 1 попадание.
Тогда Ā – событие, при котором число «успехов» равно нулю, т.е.стрелок все 5 раз «промазал».
0 0 5 5
Р(А) = 1- Р(Ā) = 1- Р5(0) = 1- С5·0,1·0,9 = 1- 0,9 ≈ 1-0,5905 ≈ 0,4095
Ответ: 0,4095.
Слайд 78Задача 39.В следующих испытаниях найдите
вероятности «успеха» и «неудачи»:
а) Бросают пару
б) Бросают игральный кубик.
«Успех» – выпадение числа,
кратного трем.
в) Бросают пару различных кубиков.
«Неудача» – выпадение двух
четных чисел.
г) Из 36 игральных карт берут 5.
«Успех» – среди них нет дамы пик.
Слайд 80Задача 40.Напишите формулы,
по которым
следует находить вероятность того, что при
а) ровно 2 раза
б) ровно 3 раза
в) ровно 4 раза
г) не выпадет ни разу
д) вычислите вероятности
этих событий
Слайд 81 2
а) С4 ·(1)·(5) ; 0,1157
6 6
3 3
б) С4 ·(1)·5 ; 0,0154
6 6
4 4
в) С4 ·(1) ; 0,00077
6
0 4
г) С4· (5) ; 0,4822
6
Слайд 82Задача 41.Из набора домино случайно вытаскивают одну «доминошку», записывают сумму очков
и возвращают ее обратно.
Так делают 3 раза.
Найдите вероятность того, что:
а) дубль появляется ровно 1 раз;
б) дубль появляется ровно 2 раза;
в) дубль появляется хотя бы раз;
г) сумма очков на «доминошке» каждый раз больше 9.
Слайд 85Задача1. 30 абитуриентов на 4 вступительных экзаменах набрали
в сумме такие
Составьте общий ряд данных, выборку результатов, стоящих
на четных местах и соответствующий ряд данных.
Слайд 86
После получения «2» дальнейшие экзамены не сдаются, поэтому сумма баллов не может быть меньше 12 (12 – это 4 «тройки»).
Значит общий ряд данных состоит из чисел 12,13,14,15,16,17,18,19,20.
Выборка состоит из 15 результатов 19,13,17,14,20,19,20,…,расположенных на четных местах.
Ряд данных – это конечная возрастающая последовательность 13,14,17,19,20.
Слайд 87Задача 2.После группировки данных эксперимента
получилась таблица их распределения:
а) определите объем
б) найдите наиболее часто
встретившуюся варианту;
в) допишите к таблице третью
и четвертую строки из частот
и процентных частот вариант;
г) найдите сумму чисел в третьей
и четвертой строках.
Слайд 89Задача 3.В нашем классе были собраны данные
о месяцах рождения учеников:
б) допишите к таблице третью
и четвертую строки из частот
и процентных частот вариант;
в) укажите наиболее и наименее
часто встретившуюся варианту.
Слайд 90Задача 4.Выборка состоит из всех букв, входящих в двустишие:
И судьба сосны ясна…».
а) выпишите ряд данных выборки;
б) найдите объем выборки;
в) определите кратность
и частоту варианты «о»;
г) какова наибольшая процентная
частота вариант выборки?
Слайд 91
а) а, б, в, д, е, и, н,
о, р, с, т, у, ы, ь, э, я
б) 30
в) 4; 2
15
г) 20% (буква «с»)
Слайд 92Задача 5. Постройте график распределения частот
и многоугольник частот по результатам
6,7,8,8,2,6,7,9,7,5,9,8,2,6,6,3,7,7,6,6.
Слайд 93 Решение.
Дана выборка объема 40. Ее ряд данных – 2,3,5,6,7,8,9,10.
Оценка
Сделав то же для других оценок, найдем их кратности: 5,3,2,11,9,4,5,1
(можно проверить: 5+3+2+11+9+4+5+1 = 40).
Частота появления двух баллов равна 5 = 1 = 0,125 = 12,5%.
40 8
Вычислив остальные частоты, составим таблицу и строим графики.
Слайд 94
11
10
9
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8 9 10 варианта
Кратность варианты
Многоугольник распределения
кратностей
Частота
варианты
0 1 2 3 4 5 6 7 8 9 10 варианта
0,75
0,5
0,25
0,1
Многоугольник распределения
частот
Мода
Размах
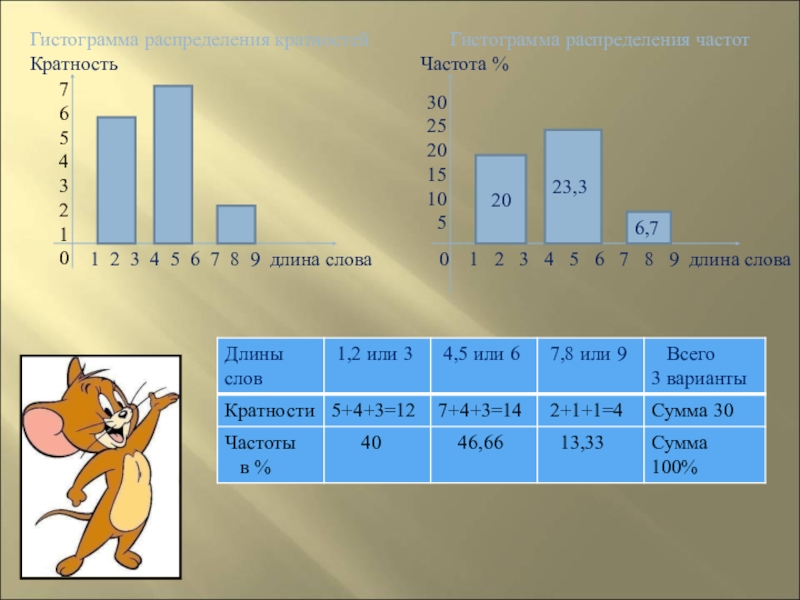
Слайд 95Задача 6.Измерили длины слов
(количество букв)
в приведенном отрывке поэмы
А.С.Пушкина «Медный всадник».
Построить
распределения кратностей и частот,
выбрав интервалы 1-3, 4-6,7-9
для вариант выборки.
«…Ужасен он в окрестной мгле! 6,2,1,9,4
Какая дума на челе! 5,4,2,4
Какая сила в нем сокрыта, 5,4,1,3,7
А всем коне какой огонь! 1,1,3,4,5,5
Куда ты скачешь, гордый конь, 4,2,7,6,4
И где опустишь ты копыта?...» 1,3,8,2,6
Слайд 96Гистограмма распределения кратностей
Кратность
7
6
5
4
3
2
1
0
1 2 3 4 5 6 7 8
Гистограмма распределения частот
Частота %
30
25
20
15
10
5
0 1 2 3 4 5 6 7 8 9 длина слова
20
20
23,3
6,7
Слайд 97Задача 7.Алфавит разбит по порядку
на три одинаковых участка:
№1 от
№2 от к до у,
№3 от ф до я.
а) найти кратность и процентную
частоту участка №3;
б) составьте таблицу распределения частот участков;
в) укажите участок наибольшей частоты;
г) постройте гистограмму частот
с выбранным распределением
на участки.
Слайд 99Задача 8.В вашем классе соберите данные
о днях рождения учеников.
а) разбейте общий
на три участка:
№1 – 1-10, №2 – 11-20,
№3 – 21-31, и составьте таблицу
распределения частот;
б) постройте соответствующую гистограмму;
в) рассмотрите шесть участков:
№1 – 1-5, №2 – 6-10,…,№6 – 26-31, и составьте таблицу
распределения частот;
г) постройте соответствующую гистограмму.
Слайд 100Задача 9. 10 девятиклассников получили за тест по комбинаторике баллы 9,14,12,9,15,12,9,15,12,12
из 20 возможных.
Найти среднее значение выборки
результатов теста, размах и моду.
Слайд 101
По правилу нахождения среднего арифметического:
9+14+12+9+15+12+9+15+12+12 = 119 = 11,9
10 10
По общему правилу нахождения
среднего значения выборки:
9·3+12·4+14·1+15·2 =
10
= 9·0,3+12·0,4+14·0,1+ 15·0,2 =11,9
Всего имеется 10 результатов, самый маленький – 9,
самый большой – 15. Размах 15-9 = 6.
Мода (часто встречающееся значение в выборке) – 12
(эта варианта встречается 4 раза).
Ответ: 11,9; 6; 12.
Слайд 102Задача 10.У 25 ребят спросили, сколько в среднем часов в день
Определите : а) размах; б) моду;
в) среднее арифметическое выборки; г) постройте многоугольник частот,
и укажите на нем данные
из пунктов а)-в).
Слайд 104Задача 11.Деталь по плану должна
весить 431г.
Контроль при взвешивании
2000 деталей
дал такие результаты:
а) составьте таблицу распределения
частот в процентах;
б) постройте многоугольник частот
(для удобства из всех вариант
вычтите по 431);
в) каков процент деталей, вес которых отличается от планового
не более, чем на 2г.
Слайд 106Задача 12.
В таблице приведены данные опроса, который проводился среди девятиклассников,
Какова доля многодетных семей (то есть имеющих 3 и более детей) среди опрошенных?
Слайд 107Решение. Чтобы найти долю многодетных семей, поделим количество многодетных семей на
Ответ: 0,14.
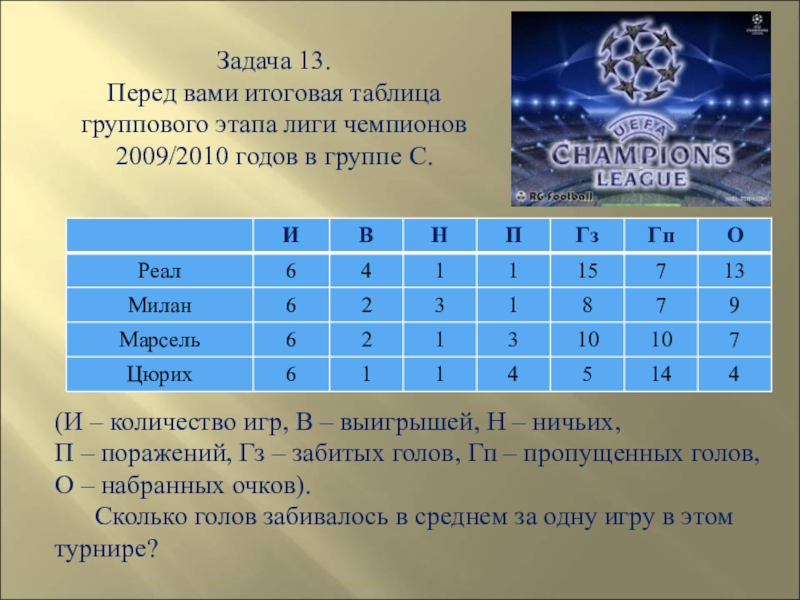
Слайд 108Задача 13.
Перед вами итоговая таблица группового этапа лиги чемпионов 2009/2010
(И – количество игр, В – выигрышей, Н – ничьих,
П – поражений, Гз – забитых голов, Гп – пропущенных голов, О – набранных очков).
Сколько голов забивалось в среднем за одну игру в этом турнире?
Слайд 109
Решение. Чтобы найти среднее количество голов за игру, нужно поделить общее
Чтобы найти количество голов, нужно сложить числа в столбце «Гз» или «Гп» (но не то и другое вместе!):
15 + 8 + 10 + 5 =38. Среднее количество голов за игру равно
Ответ: 3
1
6
1
6
Слайд 110Задача 14.
В таблице указано количество книг, прочитанных каждым из учеников
Найдите среднее арифметическое, медиану и моду этого набора чисел.
Слайд 111
Решение. Среднее арифметическое
Чтобы найти медиану, числа нужно упорядочить:
0, 1, 3,
Мода – это число, которое повторяется чаще остальных, то есть 8.
Ответ: 5,125; 5,5; 8.
5
Слайд 112Задача 15.
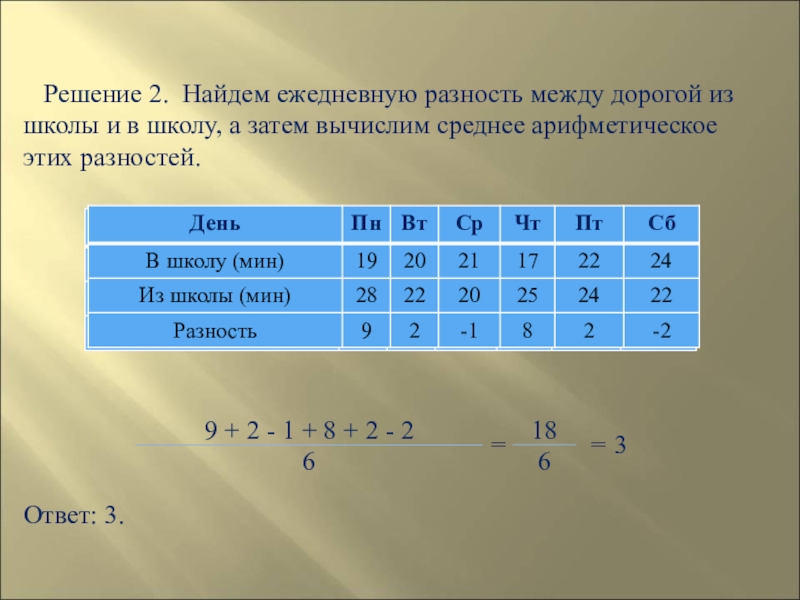
Ученик засекал в течение недели время, которое он тратит
На сколько минут в среднем дорога из школы дольше дороги в школу?
Слайд 113
Решение 1. Найдем среднюю продолжительность дороги в школу, затем - среднюю
23,5 – 20,5 = 3.
Ответ: 3.
Слайд 114 Решение 2. Найдем ежедневную разность между дорогой из школы
Ответ: 3.
Слайд 115Задача 16.
В течение четверти Таня получила следующие отметки
одну «2»;
шесть «3»;
три «4»;
и пять»5»
Найдите среднее арифметическое и моду её оценок.
Слайд 116
Решение. Каждую из оценок нужно взять в том количестве, сколько раз
чаще всего повторяется оценка «3», поэтому мода равна 3.
Ответ: 3,8; 3.
Слайд 117Задача 17.
Президент компании получает зарплату 100 000 р.
в месяц, четверо
Слайд 118
Решение. Как и в предыдущей задаче, каждую зарплату нужно взять с
Чтобы найти медиану, представим, что все 25 зарплат выписаны по возрастанию. Тогда в середине, очевидно, окажутся зарплаты по 10 000 рублей, поэтому медиана равна 10 000.
Ответ: 15 200; 10 000.
Слайд 119Задача 18.
Какое из следующих утверждений неверно:
1) если набор состоит из одинаковых
2) если набор состоит из одинаковых чисел, то его среднее арифметическое и медианы равны;
3) если размах набора равен 0, то он состоит из одинаковых чисел;
4) если среднее арифметическое и медиана набора равны, то он состоит из одинаковых чисел.
Слайд 120
Решение. Любой симметричный ряд обладает таким свойством, например: 1, 2, 3,
Ответ: неверно утверждение 4.
Слайд 121Задача 19.
Средний возраст участников школьного хора составляет
14 лет. Каких участников
Слайд 122Ответ: невозможно ответить по этим данным. Возможны все три ситуации, например,
Слайд 123Многоугольник распределения кратностей
Кратность
11 варианты
10
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 10 Варианта
Рис. 1
Слайд 124Многоугольник распределения частот
Частота
варианты
0,75
0,5
0,25
0,1
0 1 2 3 4 5 6 7 8 9 10 Варианта
Рис. 2
Слайд 125Задача 20.
В классе 40 учеников. Во время урока
С помощью транспортира определите число школьников в каждой группе.
Слайд 126Решение. Угол сектора диаграммы, соответствующего второй группе (футбол), очевидно, равен 180°.
развернутого угла. Поэтому в футбол играет половина всех школьников, то есть 20 человек.
Угол сектора диаграммы, соответствующего первой группе (баскетбол), равен 36°. Он составляет
развернутого угла. Поэтому в баскетбол играет десятая часть всех школьников, то есть 4 человека. Оставшиеся школьники, 40 – 20 – 4 = 16 человек, занимаются легкой атлетикой. Это же число можно получить из нашей диаграммы. Угол сектора диаграммы, соответствующего третей группе (легкая атлетика), равен 144° Он составляет развернутого угла.
Поэтому занимаются легкой атлетикой всех школьников, то есть х 40 = 16 человек.
2
5
2
5
Слайд 127Задача 21.
Владелец газетного киоска решил выяснить, кто чаще
Слайд 128
1) Сколько газет купили женщины в понедельник?
2)
3) Представьте данные о продажах в виде таблицы.
4) Владелец киоска думает, что женщины покупают газеты чаще, чем мужчины. Подтверждают ли данные о продажах это мнение?
Слайд 130
Задача 22.
По заданию учителя в ноябре школьник проводил
Какой день из указанных был самым холодным?
Какова была температура воздуха на улице в этот день?
Каким является это значение температуры в ряду значений температур – наибольшим или наименьшим?
Найдите размах температур за период с 3 по 12 ноября.
Слайд 131Решение.
Самым холодным было 10 ноября, когда температура была
Самым «теплым» было 12 ноября, когда температура была равна - 2°. Размах набора чисел – это разность между наибольшими и наименьшими числами из этого набора. В нашем случае размах равен (-2) – (-10) = 8 (градусов)
Слайд 132Задача 23.
Контрольную работу по математике писали 32 школьника.
и подсчитайте средний балл за контрольную.
Слайд 135Задача 24.
Среднее арифметическое числового набора равнялась 10, медиана 12, размах
Чему стали равны среднее арифметическое, медиана, размах полученного набора?
Слайд 136Решение. После умножения на 3 все характеристики тоже умножились на 3:
Ответ: 35; 41; 15.
Слайд 137Задача 25.
Завод по производству CD-дисков в течение рабочей недели (5 дней)
Сколько бракованных дисков можно ожидать в партии из
10 000 дисков?
Слайд 138Решение. Найдём долю бракованных дисков среди всех отобранных:
8+12+5+7+10 = 42 =
200·5 1000
В партии из 10 000 дисков следует ожидать 10000·0,042=420 бракованных.
Ответ: 420
Слайд 139Задача 26.
В таблице показаны средний балл и количество участников выпускного экзамена
Найдите средний балл выпускного экзамена по всему городу
Слайд 140Решение. Что бы найти средний балл по городу нужно взять средний
60·60+54·70+68·30+72·50+54·70 = 16800 = 60
60+70+30+50+70 280
Ответ: 60.
Слайд 141Задача 27.
Поезда прибывали на станцию метро со
2 мин. 8 с;
1 мин. 58 с;
2 мин. 10 с;
1 мин. 57 с;
2 мин. 12 с.
Найдите среднее арифметическое и медиану интервалов движения поездов.
Слайд 142Решение. Исходный набор не совсем числовой: каждый интервал выражен в смешанных
128, 118, 130, 117, 132.
Теперь найдём среднее в секундах:
128+118+130+117+132 = 625 = 125 с.
5 5
Можно снова перейти к смешанным единицам: среднее арифметическое равно 2 мин. 5 с. Медиана равна 2 мин. 8 сек.
Ответ: 2 мин. 5 с; 2 мин. 8 с.
Слайд 143Задача 28.
Средний возраст 11 игроков футбольного клуба «Динамо», вышедших
Слайд 144Решение. Если обозначить через x возраст игрока, ушедшего с поля, а
x-y. По условию задачи эта разность равна 26-25=1
11
Отсюда x-y=11
Ответ: 11
Слайд 145Задача 29.
Числовой набор состоит из всех двухзначных нечётных чисел: 11,
Найдите его среднее арифметическое и медиану.
Слайд 146Решение. Данный набор образует арифметическую прогрессию с первым членом 11 и
Сумму всех чисел набора можно найти как сумму арифметической прогрессии:
11+99 · 50=2750.
2
Отсюда среднее арифметическое равно
2750 = 55; медиана равна 55.
50
Ответ: 55; 55.
Слайд 147Задача 30.
Средний рост в 9 «А» классе
1) В классе обязательно есть ученик с ростом 156 см.
2) В классе обязательно есть ученик с ростом 154 см.
3) В классе обязательно есть ученик с ростом менее 154 см.
4) В классе обязательно есть ученик с ростом более 156 см.
Слайд 148Решение. Чтобы показать, что утверждения 1-3 не обязательно должны выполнятся, приведём
1) 154, 154, 160;
2) 153, 153, 155, 163;
3) см. пример для 1).
А вот утверждение 4) будет выполнено: если в классе нет учеников выше 156 см, то их средний рост может равняться 156 см только в том случае, если все они имеют такой рост. Но тогда и медиана будет равна 156 а не 154.
Ответ: справедливо утверждение 4
Слайд 149Задача 31.
При каких значениях a в числовом
а) медиана будет равняться 3?
б) среднее арифметическое будет равняться 3?
в) среднее арифметическое будет совпадать с медианой?
Слайд 150а) а≥3. При а
5
в) а=0; а=2,5; а=5. Медиана приведённого числового набора равна:
2 при а≤2, а при 2<а<3, 3 при а≥3 Среднее арифметическое равно:
1+2+3+4+а .
5
Получаем 3 уравнения с соответствующими условиями на а:
1+2+3+4+а = 2 (а≤2);
5
1+2+3+4+а = а (2<а<3);
5
1+2+3+4+а = 3 (а≥3).
5
Их корни и будут ответом.
Слайд 151Задача 32.
Три девятых класса писали итоговую контрольную работу по
Очевидно, что полностью восстановить по этим данным невозможно. А можно ли определить, в каких классах были двойки а в каких не было?
Слайд 152Решение. Объясним ответ для каждого класса.
9 «А»: если размах 3,
9 «Б»: поскольку размах 2, то все оценки лежат либо от 2 да 4, либо от 3 до 5. (Причём концы диапазонов обязательно присутствуют.) Для диапазона от 2 до 4 среднее не может равняться 4, поэтому лежат
от 3 до 5.
9 «В»: поскольку размах 2, то все оценки лежат либо от 2 до 4, либо
От 3 до 5 (Причём концы диапазонов обязательно присутствуют.) Предположим, что это диапазон от 2 до 4; тогда четвёрок должно больше половины всех оценок (ведь 4 - медиана, а пятёрок в этом случает нет вообще), но тогда 3 не может быть модой – пришли к противоречию. Значит все оценки лежат от 3 да 5.
Ответ: 9 «А» - были, 9 «Б» и 9 «В» - не было.
Слайд 153Задача 33.
Из урожая картофеля, собранного на одной из
6, 9, 5, 10, 7, 9, 8, 10, 9, 10, 8, 11, 9, 12, 9, 10, 8, 10, 11, 9, 10, 9, 8, 7, 11.
Требуется построить вариационный ряд, столбчатую диаграмму (вариант; частота), полигон относительных частот.
Слайд 154Решение. Чтобы разобраться в этих данных, расположим из в порядке возрастания
Тогда столбчатая диаграмма имеет вид:
Слайд 155
Для построения полигона сначала вычислим относительные частоты, и их значения представим
На основании полученных данных строим полигон относительных частот (частностей):
Относительные
частоты
Количество глазков в картофеле
Слайд 156Задача 34.
Осуществляя в 10 пробирках реакцию этерификации
Слайд 157Решение. Для начала проранжируем
данный ряд: 2,5; 2,5; 3; 3; 4;
Тогда хв = 2,5·2+3·2+4·3+4,5·1+5·2 = 3,75 г.
10
Ответ: 3,75 г.
Слайд 158Задача 35.
Специалист страховой компании подготовил отчёт
сообщили о двух новых страховых случаях: на 5216 руб. и на 12074 руб.
Определите новый размер
ущерба.
Слайд 159Решение. Общая сумма ущерба по пяти страховым случаям равна 5 х
48580 = 6940 руб.
7
Ответ: 6940 рублей.
Слайд 160Задача 36. Торговая компания хочет понять сколько денег тратят её
покупатели
следующие суммы (в руб.):
108; 54; 62; 74; 40; 38; 85; 92; 64; 25; 80; 143; 50; 63; 38; 79; 155; 28; 61; 83; 62;
42; 76; 47; 70; 83; 35; 192; 140; 52; 64; 88.
Компанию не интересует точная сумма S, указанная в чеке; для неё покупки
делятся на мелкие (10≤S<50), средние (50≤S<100), крупные (100≤S<200). При этом компания имеет в виду, что никто из её покупателей не тратит меньше
10 рублей и (за крайне редким исключением) больше 200 рублей.
1) Заполните следующею таблицу
Во 2 столбце отмечайте каждую покупку чёрточкой формируя у них квадрат с
диагоналями: так фигура - символизирует 2 покупки, - 4 покупки, а
фигура Х - 6 покупок.
Слайд 1612) Какие покупки, мелкие, средние или крупные, делаются чаще всего?
3) Что
таблицы (не используя исходные данные о точной сумме каждой покупки)?
Слайд 162Решение.
1) Таблица с результатами подсчётов выглядит следующим образом.
2) Из этой таблицы
3) Про сумму S одной мелкой покупки мы знаем лишь то что 10≤S<50. Про общую сумму
Sм, потраченную на 8 мелких покупок, мы можем сказать лишь то что 80≤Sм<400.
Аналогично, относительно общей суммы Sс , потраченных на все 19 средних покупок
мы можем сказать лишь то, что 950≤Sс<1900, а про общую сумму Sк , потраченную на все
5 крупных покупок, мы можем сказать лишь то, что 500≤Sк<1000. Складывая три этих
неравенства, для общих расходов Sобщ= Sм+Sс+Sк мы получим двойное неравенство:
1530≤Sобщ<3300. Средняя сумма одной покупки равна Sобщ
32
На основе данных таблицы мы можем утверждать лишь то, что эта величина находится в
пределах от 1530 ≈ 47 руб. 81 коп. до 3300 ≈ 103 руб. 13 коп.
32 32
Слайд 163Задача 37. В классе 12 мальчиков и 10 девочек. Учительница задала
20 задач на сложение двузначных чисел в уме. В таблице 1 приведены результаты этого
теста для мальчиков, а в таблице 2 - для девочек.
Слайд 164 Подсчитайте среднее число правильно решённых задач одним
Можно ли с помощью этих результатов определенно сказать, кто лучше считает в уме – мальчики или девочки?
Слайд 165Среднее число правильно решённых задач одним мальчиком равно:
х= 15+12+8+16+14+11+17+7+16+20+15+14 = 165
12 12
Среднее число правильно решённых задач одной девочкой равно:
y= 17+15+14+16+13+17+16+12+14+16 = 150 = 15.
10 10
Для мальчиков наибольшее число правильно решённых задач равно 20, а наименьшее равно 7. Поэтому для мальчиков размах числа правильно решённых задач равен 20-7=13.
Для девочек наибольшее число правильно решённых задач равно 17, а наименьшее равно 12. Поэтому для девочек размах числа правильно решённых задач равен 17-12=5.
Таким образом, для девочек среднее число правильно решённых задач одним человеком больше чем для мальчиков. Кроме того, значения размахов показывают, что результаты девочек разбросаны гораздо меньше, то есть более стабильны. Поэтому разумно сделать вывод, что девочки этого класса лучше считают в уме, чем мальчики.
Слайд 167Задача 1. В первый ящик положили
5 мобильников,
а во второй
Сколькими способами можно вытащить
один мобильник?
Слайд 168
Из 1 ящика можно вытащить
пятью способами, а из 2 – тремя способами.
Всего существует 5+3 = 8 способов.
Ответ: 8.
Слайд 169Задача 2. В первом ящике
5 мобильников с зеленым корпусом,
а
с красным корпусом.
Сколькими способами можно вытащить один зеленый и один красный мобильник?
Слайд 170
Зеленые мобильники можно выбрать
пятью способами, красные – тремя способами.
Всего 1 зеленый и 1 красный можно выбрать
3 · 5 = 15 способами.
Ответ: 15.
Слайд 171Задача 3. Сколько не более чем трехзначных чисел можно составить из
не повторялись?
Слайд 172 Решение.
Надо узнать, сколько можно составить
однозначных, двузначных или трехзначных чисел.
Однозначных чисел будет 5, значит, N1 = 5.
На месте десятков двузначных чисел можно поставить
любую из пяти цифр.
После каждого такого выбора на месте единиц
можно поставить любую из четырех оставшихся цифр,
т.к. цифры в числе не должны повторяться.
По правилу произведения N2 = 5·4 = 20.
Рассуждая аналогично,
получим число различных трехзначных чисел
N3 = 5· 4· 3 = 60.
Следовательно, N = 5+20+60 = 85.
Слайд 173Задача 4.В одной вазе лежит
5 яблок,
а в другой
Сколькими способами можно выбрать:
а) яблоко или мандарин;
б) яблоко и мандарин?
Слайд 175Задача 5.Ученик должен выполнить
практическую работу
по математике.
Ему предложили на выбор
17
по геометрии.
Сколькими способами он может выбрать одну тему
для практической работы?
Слайд 177Задача 6.В танцевальном кружке
5 мальчиков и 4 девочки.
Руководитель хочет отобрать пару, состоящую из
1 мальчика и 1 девочки
для участия в соревнованиях.
Сколько он должен
посмотреть пар, чтобы выбрать
лучшую пару?
Слайд 179Задача 7. Имеется 5 билетов
денежно-вещевой лотереи,
6 билетов спортлото
и
Сколькими способами
можно выбрать 1 билет
из спортлото
или автомотолотереи?
Слайд 181Задача 8.Сколько имеется путей,
которыми
можно попасть
из города А в
через город В, если из А в В ведут
две дороги,
а из В и С – три дороги?
Слайд 183Задача 9.На книжной полке стоят
25 книг по математике,
15 –
10 – по астрономии.
Сколькими способами можно
выбрать
3 книги так, чтобы одна книга
была по математике,
другая – по физике
и третья – по астрономии?
Слайд 186Решение.
Составим таблицу: слева от первого столбца – первые цифры искомых чисел,
5 строк · 3 столбика = 15 чисел
Ответ: 15.
Слайд 187Задача 11.Сколько двузначных чисел можно составить, используя цифры 1,4,7, если цифры
Слайд 188
При использовании правила умножения применяют схему –
дерево возможных вариантов.
Двузначное число
1 цифра числа
2 цифра числа
1
4
7
7 1 7 1 4
14,17 41,47 71,74
Ответ: 6.
Слайд 189Задача 12.На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс,
Из скольких вариантов завтрака Вова может выбирать?
Слайд 193Задача14.Служитель зоопарка должен дать зайцу
2 различных овоща.
Сколькими способами
он может
Слайд 194Завтрак зайца
1 овощ
2 овощ С К М К М С
Варианты МС, МК, СМ, СК, КМ, КС
6 вариантов, но блюда МС и СМ,
МК и КМ, КС и СК совпадают, поэтому
3 пары блюд
Ответ: 3.
Слайд 195Задача15.Туристическая фирма планирует посещение туристами
в Италии трех городов:
Венеции,
Сколько существует вариантов
такого маршрута?
Слайд 196 Маршрут
1 город
2 город Р Ф В Ф В Р
3 город Ф Р Ф В Р В
Варианты ВРФ, ВФР, РВФ, РФВ ФВР, ФРВ
Ответ: 6.
Слайд 197Задача16.Несколько стран
в качестве символа своего государства
решили использовать флаг
в
но разных по цвету:
белый, синий, красный.
Сколько стран могут использовать
такую символику при условии,
что у каждой страны свой,
отличный от других,
флаг?
Слайд 200
N = 2· 2· 2 = 8
2 способ. + горит, - не горит
+++
++-
+-+
+--
-++
---
-+-
--+
Ответ: 8.
Слайд 201Задача 18.Сколько различных пятизначных чисел можно составить
из цифр 1,2,3,4,5 при
что ни одна цифра в числе
не повторяется?
Слайд 203Задача19.В соревнованиях участвовало 4 команды.
Сколько вариантов
распределения мест между ними
Слайд 205Задача 20.Сколькими способами можно расположить
на шахматной доске
8 ладей так,
друг друга?
Слайд 207Задача 21.Сколькими способами
можно разместить 12 человек
за столом,
возле которого
12 стульев?
Слайд 211Задача 23.Сколько двузначных чисел можно составить из пяти цифр 1,2,3,4,5 при
из них не повторяется?
Слайд 212
Т.к. двузначные числа отличаются друг от друга
или самими цифрами, или их порядком,
то искомое количество равно
числу размещений из пяти элементов по два:
А²5 = 5· 4 = 20
Ответ: 20.
Слайд 213Задача 24.У нас есть 9 книг
из серии
«Занимательная математика».
Сколькими
Слайд 215Задача 25.Сколько существует вариантов
распределения трех призовых мест,
если в розыгрыше участвуют
7
Слайд 217Задача 26.Сколько вариантов расписания
можно составить на один день,
если всего имеется
8
а в расписании на день
могут быть включены
только три из них?
8
Слайд 219Задача 27.Сколько вариантов распределения
трех путевок в санатории
различного профиля
можно
для пяти претендентов?
Слайд 221Задача 28.В городе проводится
первенство по футболу.
Сколько в нем состоится
если участвуют
12 команд?
Слайд 223Задача 29.Сколько
различных музыкальных фраз
можно составить
из 6 нот,
если не допускать
повторения звуков?
Слайд 224 Музыкальные фразы отличаются
одна от другой или нотами, или их порядком.
Считаем, что фортепиано имеет 88 клавиш.
6
А88 = 88! = 390190489920
(88-6)!
Ответ: 390190489920.
Слайд 225Задача 30.Сколько сигналов можно подать
5 различными флажками,
поднимая их в любом количестве
и
Слайд 226 1 2
А5+А5+А5+А5+А5= 5! + 5! + 5! + 5! + 5! = 325
(5-1)! (5-2)! (5-3)! (5-4)! (5-5)!
Ответ: 325.
Слайд 227Задача 31.В тренировках участвовали
12 баскетболистов.
Сколько различных стартовых пятерок
может образовать
Слайд 233Задача 34.Сколькими способами можно
составить дозор
из трех солдат и одного офицера,
80 солдат и 3 офицера?
Слайд 234 3
С80 · С3 = 80! · 3! = 77!·78·79·80·3! = 246480
(80-3)!3! (3-1)!1! 77!·3!·2!
Ответ: 246480.
Слайд 235Задача 35.Сколькими способами можно
выбрать двух человек в президиум,
если на собрании присутствует
78
Слайд 238
Т.к. порядок цифр в числе существенен, цифры могут повторяться,
то будут размещения с повторениями из 5 элементов по 3,
а их число равно
~3 3
А5 = 5 = 125
Ответ: 125.
Слайд 239Задача 37. В кондитерском магазине продают 4 сорта пирожных: эклеры, песочные,
Сколькими способами можно купить
7 пирожных?
Слайд 240Решение.
Покупка не зависит от того, в каком порядке укладывают пирожные в
~7
С4 = (7+4-1)! = 10! = 120
7!(4-1)! 7!3!
Ответ: 120.
Слайд 242Решение.
Всего 6 букв. Одинаковые буквы
n«а» = 3, n«н» = 2, n«с»
Р6(3,2,1) = 6! = 60
3!2!1!
Ответ: 60.
Слайд 244Решение.
Если бы девушки стояли на месте, то их было бы
Р7 =
Но т.к. танцующие кружатся, то их положение относительно окружающих не имеет роли,
важно лишь взаимное расположение, т.е.перестановки, переходящие друг в друга.
Но из каждой перестановки можно получить еще 6 путем вращения - 7 мест
5040 : 7=720 различных перестановок девушек в хороводе.
Р(вр.7) = (7-1)! = 720
Ответ: 720.
Слайд 246
Ожерелье можно не только вращать, но и перевернуть.
Р(вр.и пов.) = (n-1)!
2
Р7 = (7-1)! = 6! = 720 = 360
2 2 2
Ответ: 360.
Слайд 247Задача 41.На сувениры в «Поле Чудес»
спонсоры предлагают кофеварки, утюги, телефонные аппараты,
Сколькими способами
9 участников игры могут получить
эти сувениры?
Сколькими способами могут быть выбраны 9 предметов
для участников игры?
Слайд 248 ~ 9
1) А4 = 4 = 262144
~9
2) С4 = (9+4-1)! = 12! = 220
9!(4-1)! 9!3!
Ответ: 262144; 220.
Слайд 250 Всего букв в слове 9. Одинаковые буквы
Р9(1,4,3,1) = 9! = 2520
1!4!3!1!
Ответ: 2520.
Слайд 251Задача 43.В книжный магазин поступили
романы Ф.Купера
«Прерия», «Зверобой», «Шпион»,
«Пионеры», «Следопыт»
по одинаковой
Сколькими способами
библиотека
может закупить 17 книг
на выбранный чек?
Слайд 253Задача 44.Номер автомашины состоит из трех букв русского алфавита
и трех
Сколько различных номеров
автомашин
можно составить?
Слайд 255 Используемая литература:
1.А.Н.Мордкович,П.В.Семенов.
События. Вероятности. Статистическая
3-е изд. – М.:Мнемозина,2005.
2.А.Г.Климова,И.Н.Данкова,О.П.Малютина.
Элективный курс для профильного обучения.
(10-11 классы). Начала теории вероятностей
с элементами комбинаторики и математической статистики.- Воронеж: ВОИПКРО,2006.
3.Журнал «Математика в школе» №5, №6, №7, 2011.
4.Учебно-методическая газета «Математика» №1, №7, 2008 ; №15, 2009.