- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок на тему Изгиб
Содержание
- 1. Урок на тему Изгиб
- 2. Цели урокаПовторение пройденного теоретического материалаОпределение алгоритма решения
- 3. Общие сведенияИзгибом называется вид нагружения бруса, при
- 4. Общие сведения При плоском поперечном изгибе
- 5. Если изгибающий момент Mx является единственным внутренним
- 6. Механические испытания на изгиб Испытания на изгиб
- 7. Результаты испытания на изгибРезультаты испытания на изгиб
- 8. Построение эпюр поперечной силы и изгибающего момента
- 9. Опорные реакцииПеред тем, как определять внутренние усилия
- 10. Комбинируя различные типы закреплений, можно получить ряд
- 11. Правило знаков для внутренних силовых факторов.Если внешняя
- 12. Правило построения эпюры М называется построением
- 13. На рис.6.9 показаны два случая оставшейся части:
- 14. Составь решениеУравнение момента составляется относительно оси Х,
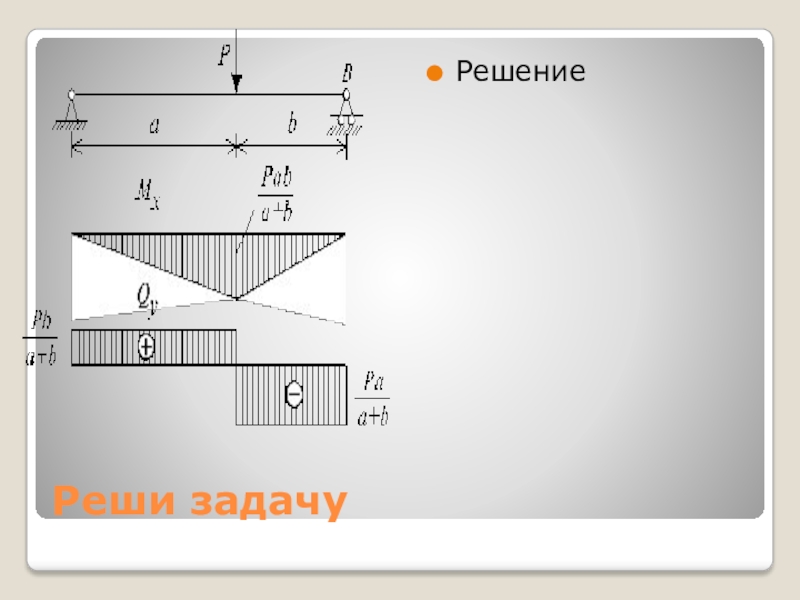
- 15. Реши задачуРешение
- 16. Основные дифференциальные соотношения теории изгибаЗапиши формулы
- 17. Спасибо за работу на уроке!
Слайд 1Изгиб
Презентация заключительного занятия
Автор: Катечкина З.В.преподаватель
общетехнических дисциплин
ГАПОУ СХТ
Слайд 2Цели урока
Повторение пройденного теоретического материала
Определение алгоритма решения задач
Тренинг решения задач
Составьте вопросы
Работа по онлайн-тесту.
Домашнее задание:
Составить 5 тестов
Слайд 3Общие сведения
Изгибом называется вид нагружения бруса, при котором к нему прикладывается
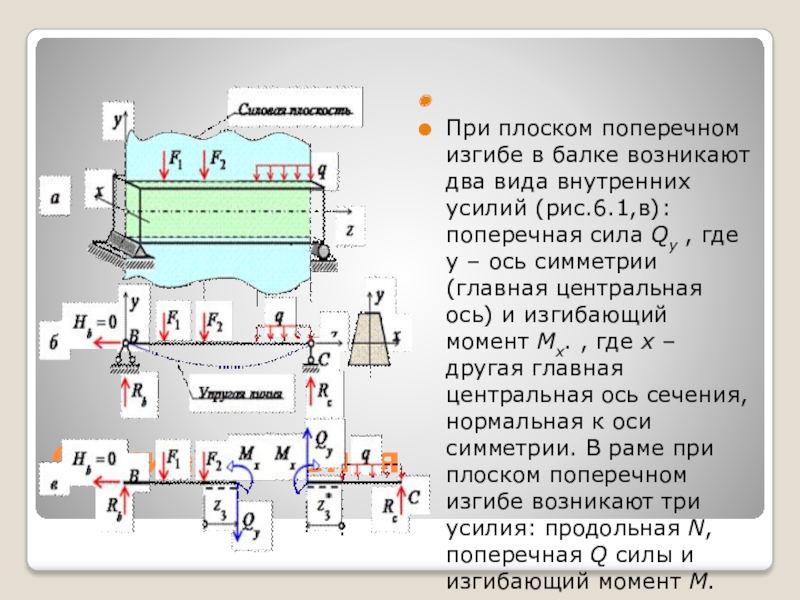
Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).
Слайд 4Общие сведения
При плоском поперечном изгибе в балке возникают два вида
Слайд 5Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой
Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.
Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.
Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.
Слайд 6Механические испытания на изгиб
Испытания на изгиб часто используются для оценки механических
Чаще всего образцы нагружают по схемам так называемого трехточечного (рис.6.3,а) и четырехточечного (рис.6.3,б) изгиба.
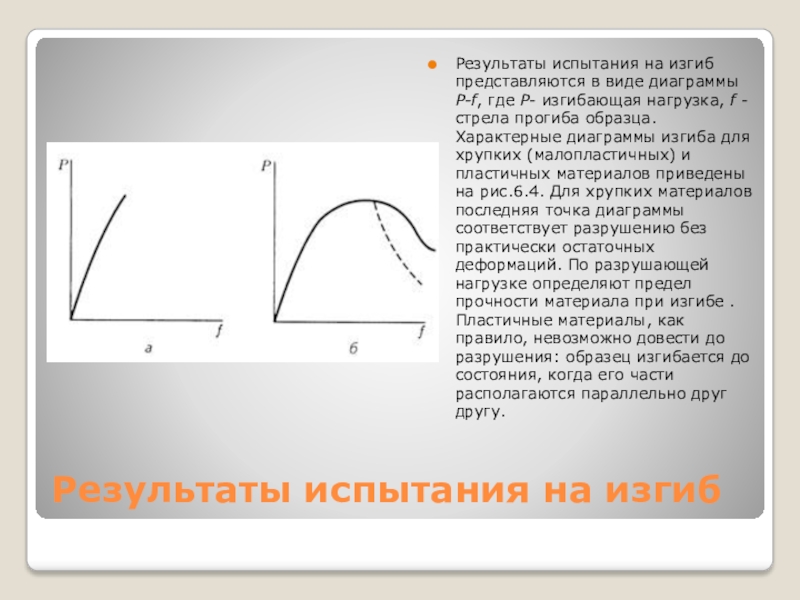
Слайд 7Результаты испытания на изгиб
Результаты испытания на изгиб представляются в виде диаграммы
Слайд 8Построение эпюр поперечной силы и изгибающего момента
Эпюра внутренней силы – график,
Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.
Последовательно на каждом участке вводится скользящая система координатных осей (начало координат совмещается с началом участка) и для произвольного сечения составляются выражения для определения поперечной силы и изгибающего момента. Затем по этим выражениям в пределах каждого участка строятся графики (эпюры) внутренних сил.
Слайд 9Опорные реакции
Перед тем, как определять внутренние усилия (поперечные силы и изгибающие
Слайд 10Комбинируя различные типы закреплений, можно получить ряд схем балок:
1. Балка шарнирно
2. Балка шарнирно опертая с консолями (С1 и С2) (рис.6.6,б). Реакции те же. Балка статически определимая.
3. Балка жестко закрепленная одним концом (консольная балка) (рис.6.6,в). В заделке три реакции. Балка статически определимая. При действии нагрузки перпендикулярной оси реакция НВ всегда равна 0.
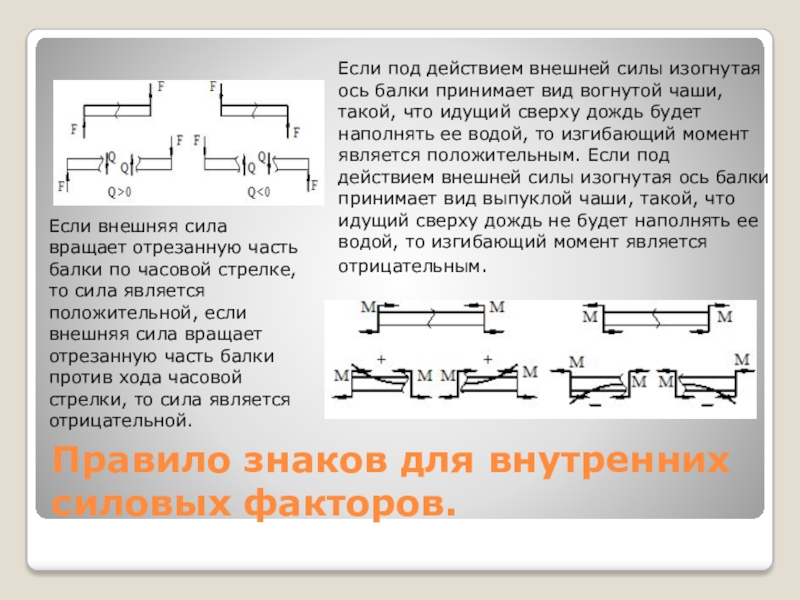
Слайд 11Правило знаков для внутренних силовых факторов.
Если внешняя сила вращает отрезанную часть
Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.
Слайд 12 Правило построения эпюры М называется построением эпюры со стороны растянутых
Достаточно очевидно и подтверждается опытом, что балка при изгибе деформируется таким образом, что волокна, расположенные в выпуклой части, растягиваются, а в вогнутой – сжимаются. Между ними лежит слой волокон, который лишь искривляется, не изменяя своей первоначальной длины (рис.6.8). Этот слой называется нейтральным или нулевым, а его след на плоскости поперечного сечения – нейтральной (нулевой) линией или осью.
Слайд 13На рис.6.9 показаны два случая оставшейся части: левая и правая.
Для определения
Изгибающий момент Mx, действующий в поперечном сечении балки, по величине равен сумме моментов всех внешних сил, приложенных к рассматриваемой отсеченной части бруса, относительно центральной оси x этого сечения:
Если внешняя сила в данном сечении растягивает нижние волокна балки, то момент этой силы в этом сечении считается положительным, если растягиваются верхние волокна балки, то момент этой силы будет отрицательным.
Поперечная сила Qy в сечении бруса, по величине равна сумме проекций всех внешних сил, действующих на отсеченную часть бруса, на ось перпендикулярную оси бруса (ось y):
Слайд 14Составь решение
Уравнение момента составляется относительно оси Х, проходящей в поперечном сечении
Рассмотрим характерный пример (рис. 6.10,а) и установим необходимые правила. Решение задачи, как правило, начинается с определения полной системы внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями (рис. 6.10,б), выполняющими ту же роль, что и опорные закрепления.
Заданная система статически определима, следовательно, из условий равновесия системы, т.е. равенства нулю суммы моментов всех сил относительно шарнирных опор (в шарнирах нет ограничений поворота сечений балки, поэтому изгибающих моментов не возникает) и , определяем вертикальные реакции в опорах:
Для определения имеем: откуда . Для проверки правильности вычислений воспользуемся условием равенства нулю суммы всех вертикальных сил откуда получим
0 = 0.