- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему решение заданий В-12 егэ
Содержание
- 1. решение заданий В-12 егэ
- 2. Тип задания: Задание на исследование функции с
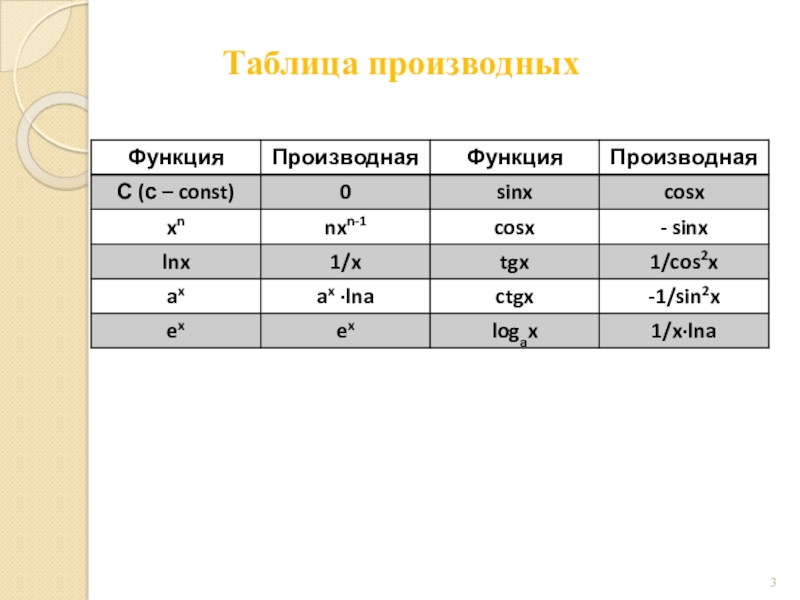
- 3. Таблица производных
- 4. Правила вычисления производных(f(x)+g(x))´=f´(x)+g´(x)(f(x)-g(x))´=f´(x)-g´(x)(f(x)·g(x))´=f´(x)·g(x)+f(x)·g´(x)(f(x)/g(x))´=(f´(x)·g(x)-f(x)·g´(x))/g2(x)(f(g(x))´=f´(g(x))·g´(x)
- 5. Алгоритм отыскания наибольшего (наименьшего) значения функции
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. 5. Найти точку минимума функции у = х – 5lnх
- 11. 6. Найти наибольшее значение функции
Тип задания: Задание на исследование функции с помощью производнойХарактеристика задания: Задание на вычисление с помощью производной экстремума данной функции или наибольшего (наименьшего) значения данной функции на заданном отрезке Комментарий: Решение задачи связано с нахождением при помощи
Слайд 2Тип задания: Задание на исследование функции с помощью производной
Характеристика задания: Задание
на вычисление с помощью производной экстремума данной функции или наибольшего (наименьшего) значения данной функции на заданном отрезке
Комментарий: Решение задачи связано с нахождением при помощи производной точек максимума (минимума) заданной функции или ее наибольшего (наименьшего) значения на отрезке. Если функция задана формулой, то при нахождении наибольшего (наименьшего) значения функции на отрезке можно использовать стандартный алгоритм
Комментарий: Решение задачи связано с нахождением при помощи производной точек максимума (минимума) заданной функции или ее наибольшего (наименьшего) значения на отрезке. Если функция задана формулой, то при нахождении наибольшего (наименьшего) значения функции на отрезке можно использовать стандартный алгоритм
Слайд 4Правила вычисления производных
(f(x)+g(x))´=f´(x)+g´(x)
(f(x)-g(x))´=f´(x)-g´(x)
(f(x)·g(x))´=f´(x)·g(x)+f(x)·g´(x)
(f(x)/g(x))´=(f´(x)·g(x)-f(x)·g´(x))/g2(x)
(f(g(x))´=f´(g(x))·g´(x)
Слайд 5Алгоритм отыскания наибольшего (наименьшего) значения функции
на заданном отрезке
Найти производную функции
Найти
значения х, при которых производная равна нулю
Выбрать из значений х, найденных в п.2 те, которые принадлежат заданному отрезку
Вычислить значения функции на концах заданного отрезка и в точках, определенных в п.3
Выбрать наибольшее (наименьшее) значение функции
Выбрать из значений х, найденных в п.2 те, которые принадлежат заданному отрезку
Вычислить значения функции на концах заданного отрезка и в точках, определенных в п.3
Выбрать наибольшее (наименьшее) значение функции