- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Проекты кружка по математике
Содержание
- 1. Презентация Проекты кружка по математике
- 2. Пояснительная запискаМетод проектов разрушает учебную рутину.На вопрос:
- 3. Приобщение учащихся к проектной деятельности с использованием
- 4. АЛГЕБРА ПОДГОТОВКА К ЕГЭ
- 5. РЕШЕНИЕ ЗАДАЧ ТИПА В4 1. Для
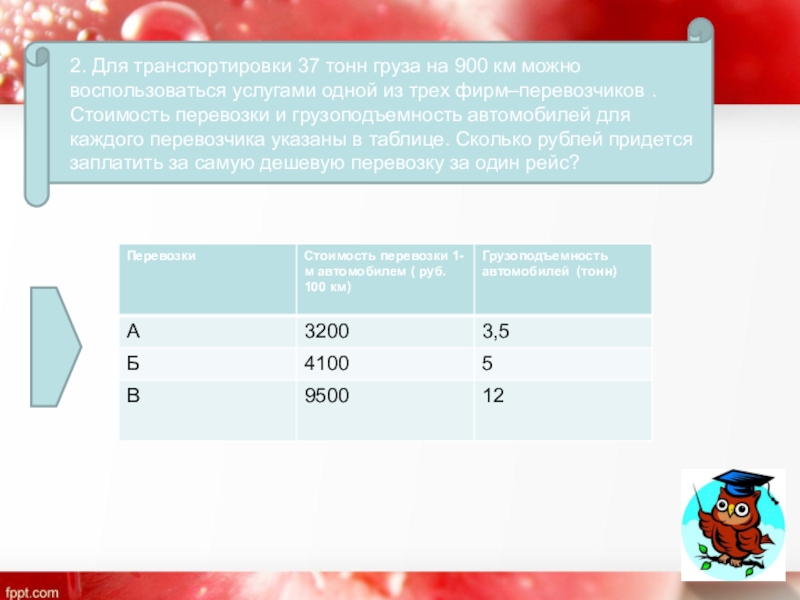
- 6. 2. Для транспортировки 37 тонн груза на
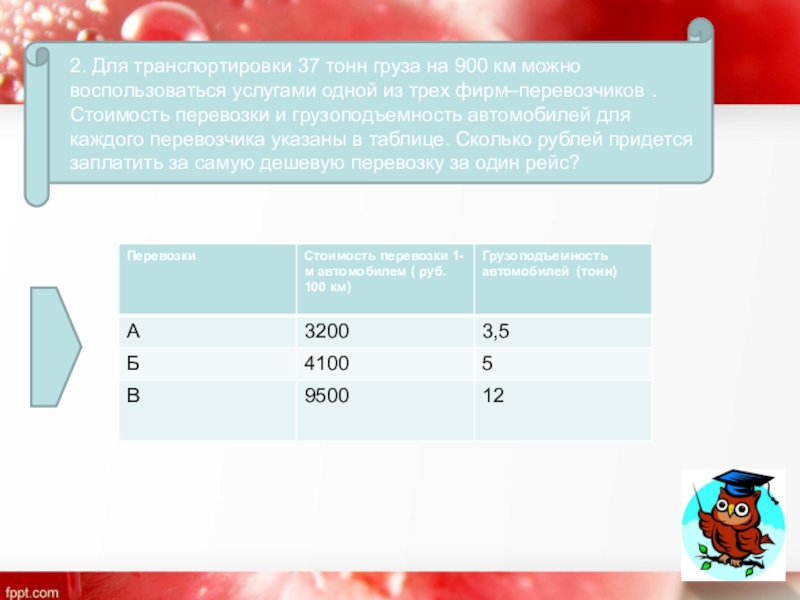
- 7. 2. Для транспортировки 37 тонн груза на
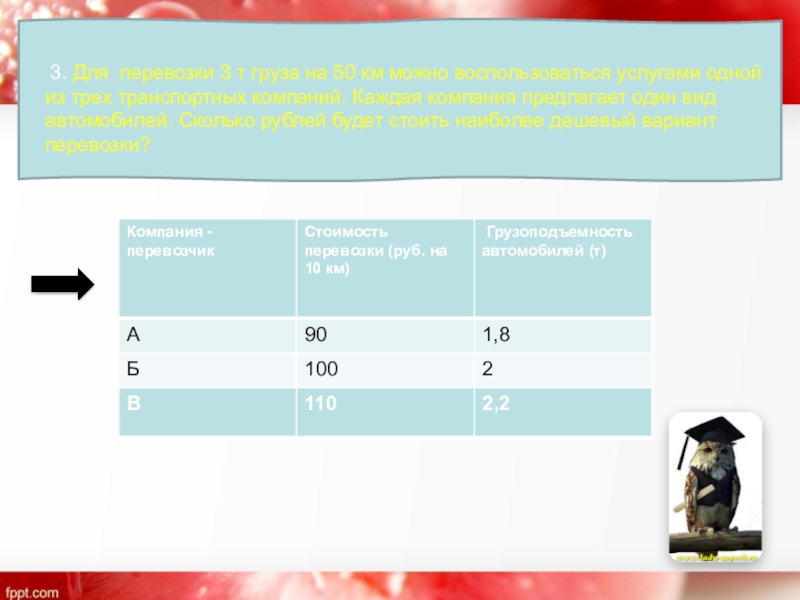
- 8. 3. Для перевозки 3 т груза
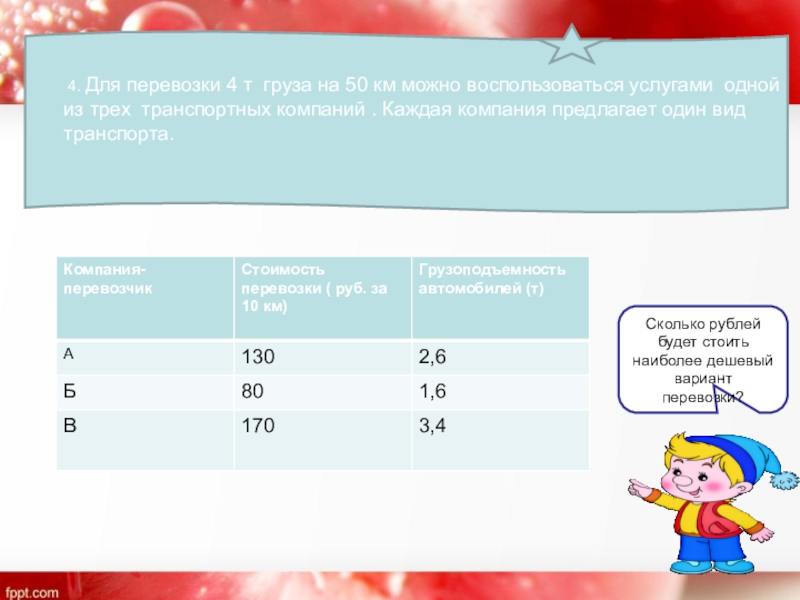
- 9. 4. Для перевозки 4 т груза
- 10. 5. Для перевозки 5 т груза на
- 11. 6. Строительный фирме нужно приобрести 72
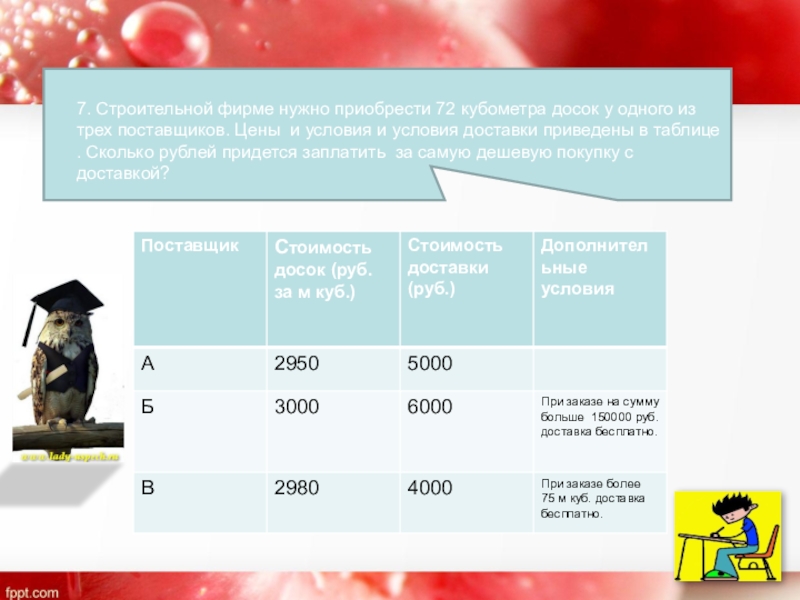
- 12. 7. Строительной фирме нужно приобрести 72 кубометра
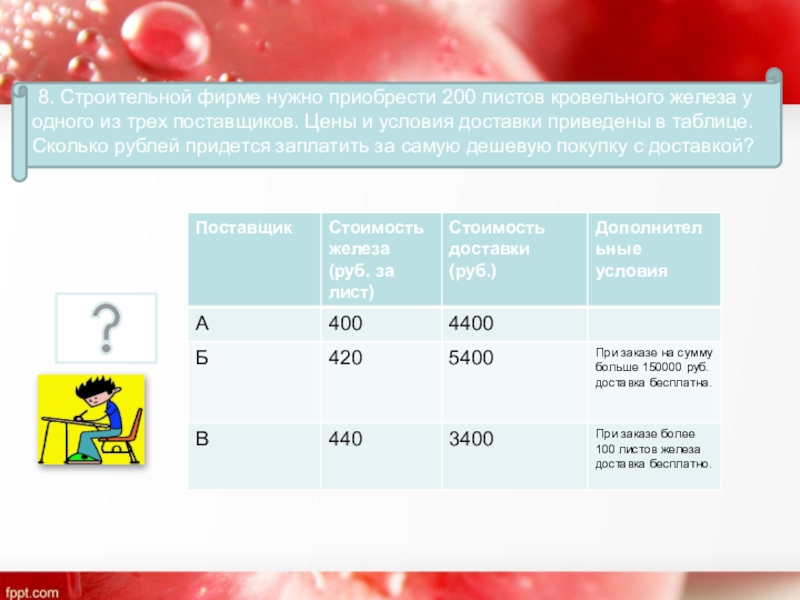
- 13. 8. Строительной фирме нужно приобрести 200
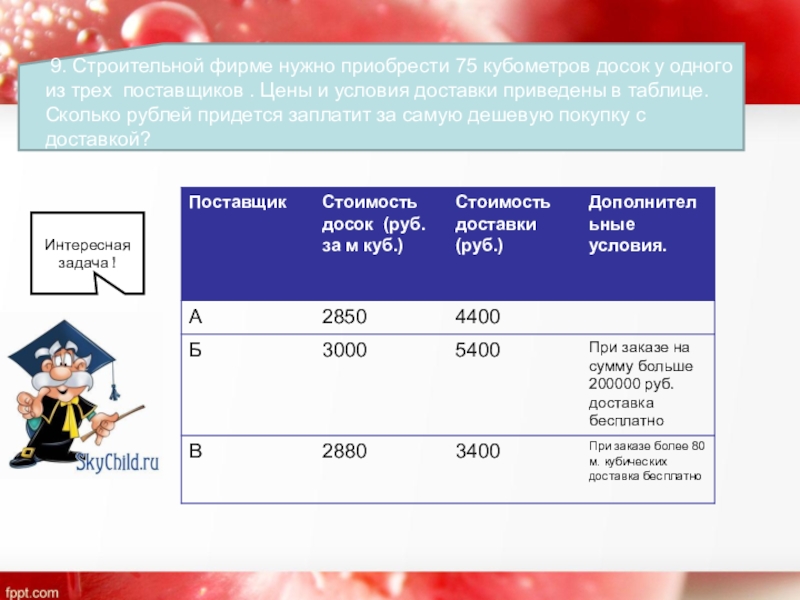
- 14. 9. Строительной фирме нужно приобрести 75
- 15. 10.Строительный подрядчик планирует купить 15 т облицованного
- 16. Геометрия автомобиля ВведениеСовременные наземные транспортные средства и
- 17. Математическая модель разгона автомобиляПри разгоне автомобиля его
- 18. Область машины где пригодятся знания по математике:Автомобильные
- 19. АВТОМОБИЛЬНЫЕ ФАРЫ:Параболоид вращения -это поверхность, которая образуется
- 20. ПОДБОР ПОРШНЕЙ ПО ЦИЛИНДРАМ Для подбора поршней
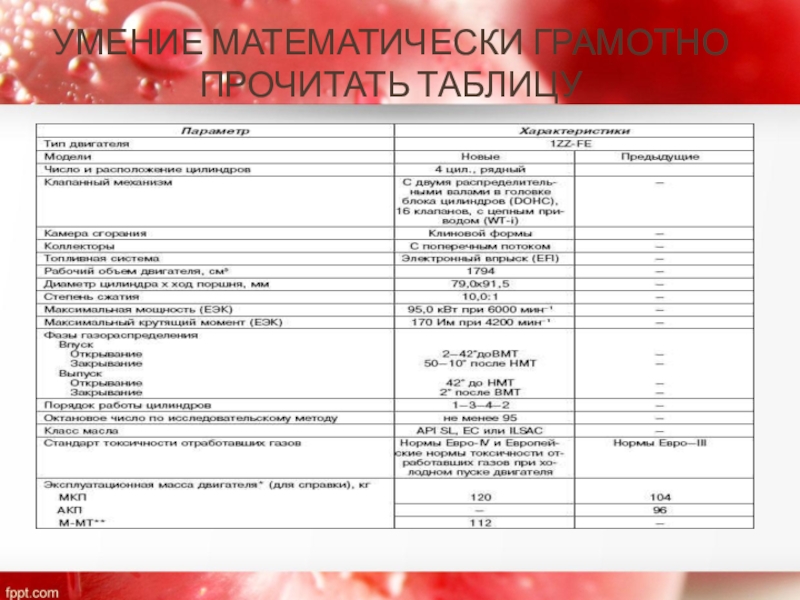
- 21. УМЕНИЕ МАТЕМАТИЧЕСКИ ГРАМОТНО ПРОЧИТАТЬ ТАБЛИЦУ
- 22. Функции в задачах с практическим содержаниемЗадачи:Рассмотреть историю
- 23. Исторические сведенияГ. Галилей(1564–1642)П. Ферма(1601–1665) Р. Декарт(1569–1650)
- 24. Функции, изучаемые в курсе математики:
- 25. Примеры применения различных функций в жизни, технике, природе y = a x + b
- 26. Примеры применения различных функций в жизни, технике, природе
- 27. Примеры применения различных функций в жизни, технике,
- 28. Примеры применения различных функций в жизни, технике, природе
- 29. Функциональные зависимости в повседневной жизниПример 2. Ежедневно
- 30. Функциональные зависимости в повседневной жизниИзменение температурного режима
- 31. Выводы:Развития понятия функции не закончено. Новые
- 32. МАТЕМАТИКА И АВТОМОБИЛЬНАЯ ПРОМЫШЛЕННОСТЬТРИГОНОМЕТРИЯ В ОКРУЖАЮЩЕМ НАС
- 33. История тригонометрии По звездам вычисляли местонахождение корабля
- 34. Сам термин косинус появился значительно позднее
- 35. Основоположник аналитической теории тригонометрических функций.
- 36. Стадии развития тригонометрии:Тригонометрия была вызвана к жизни
- 37. Где применяется тригонометрияТригонометрические вычисления применяются практически во
- 38. Тригонометрия в физикеВ окружающем нас мире приходится
- 39. Математический маятникНа рисунке изображены колебания маятника, он движется по кривой, называемой косинусом.
- 40. У музыки в автомобиле есть своя геометрияТетраэдр
- 41. С АНС Н А если рассматриваем автомобиль,
- 42. Представьте, что вы припарковали автомобиль на стоянке
- 43. Смотрим из окна автомобиля на звездное небо
- 44. Математическая модель автомобиля, математические задачи
- 45. Для технических профессий всегда необходимы задачи на
- 46. Задача на расход бензина2) Во время поездки
- 47. 3) Сколько брезента необходимо для пошива тента
- 48. Задачи на проценты1) Автомеханик установил сначала 25%
- 49. Площади и объёмы1) Определить объём кузова автомобиля
- 50. Вот такую работу мы проделали на кружке по математике «Математическое моделирование в автомобилестроении»СПАСИБО ЗА ВНИМАНИЕ!
Слайд 2Пояснительная записка
Метод проектов разрушает учебную рутину.
На вопрос: что же даёт детям
Учащиеся отвечают:
лучше усваивается материал - 73%, уроки стали интереснее - 68%, с желанием идем на урок - 53%,появилась возможность демонстрировать свои работы- 26%.
На вопрос: «Чему удалось научиться в ходе работы над проектом? Ученики отвечают:
распределять правильно время - 32%, достигать поставленной цели - 17%,выступать перед аудиторией - 16%. добывать информацию - 14%, готовить презентацию - 21%.
Мотивация обучения учащихся:
интерес к предмету – 98%;
к практическому материалу – 87%;
к области знаний (шире учебного курса) – 42%;
желание общаться с педагогом по предмету – 97,8%.
Слайд 3Приобщение учащихся к проектной деятельности с использованием компьютерно-информационных технологий позволяет наиболее
Алгебра – подготовка к ЕГЭ.
Проект по теме «Геометрия автомобиля».
3. Проект по теме «Функции в задачах с практическим и производственным содержанием».
4. Проект по теме «Математика и автомобильная промышленность».
5. Проект по теме «Математическая модель автомобиля. Математика и искусство создания автомобиля».
Слайд 5РЕШЕНИЕ ЗАДАЧ ТИПА В4
1. Для транспортировки 40 тонн груза
Слайд 6
2. Для транспортировки 37 тонн груза на 900 км можно воспользоваться
Слайд 7
2. Для транспортировки 37 тонн груза на 900 км можно воспользоваться
Слайд 8
3. Для перевозки 3 т груза на 50 км
Слайд 9
4. Для перевозки 4 т груза на 50 км можно
Сколько рублей будет стоить наиболее дешевый вариант перевозки?
Слайд 10
5. Для перевозки 5 т груза на 350 км можно воспользоваться
Слайд 11 6. Строительный фирме нужно приобрести 72 кубометра досок у одного
Слайд 12
7. Строительной фирме нужно приобрести 72 кубометра досок у одного из
Слайд 13
8. Строительной фирме нужно приобрести 200 листов кровельного железа у
Слайд 14
9. Строительной фирме нужно приобрести 75 кубометров досок у одного
Интересная задача !
Слайд 1510.Строительный подрядчик планирует купить 15 т облицованного кирпича у одного из
Слайд 16Геометрия автомобиля
Введение
Современные наземные транспортные средства и в частности автомобиль – это
Слайд 17Математическая модель разгона автомобиля
При разгоне автомобиля его массой и отдельными частями,
Математическая модель - это способ описания реальной жизненной
ситуации (задачи) с помощью математического языка.
Слайд 18Область машины где пригодятся знания по математике:
Автомобильные фары
Установка катафотов и
Какие лампы выгоднее использовать для фар
Форма шестеренки
Проверка рулевого управления
Подбора поршней по цилиндрам
Умение математически грамотно прочитать таблицу
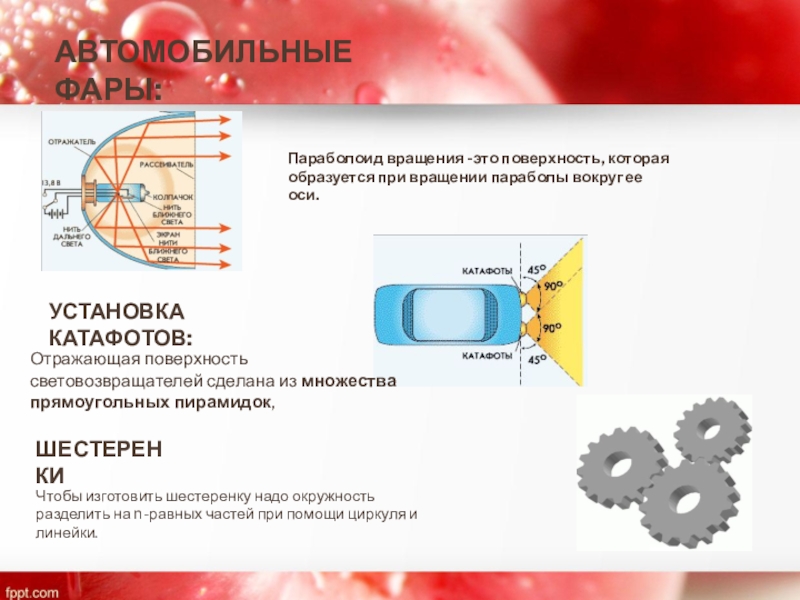
Слайд 19АВТОМОБИЛЬНЫЕ ФАРЫ:
Параболоид вращения -это поверхность, которая образуется при вращении параболы вокруг
УСТАНОВКА КАТАФОТОВ:
Отражающая поверхность световозвращателей сделана из множества прямоугольных пирамидок,
ШЕСТЕРЕНКИ
Чтобы изготовить шестеренку надо окружность разделить на n-равных частей при помощи циркуля и линейки.
Слайд 20ПОДБОР ПОРШНЕЙ ПО ЦИЛИНДРАМ
Для подбора поршней к цилиндрам вычисляют зазор
Слайд 22Функции в задачах с практическим содержанием
Задачи:
Рассмотреть историю возникновения понятия функции.
Увидеть применение
Решить задачи, связанные с применением функций и графиков.
Найти функциональные зависимости в повседневной жизни и выразить их с помощью графиков.
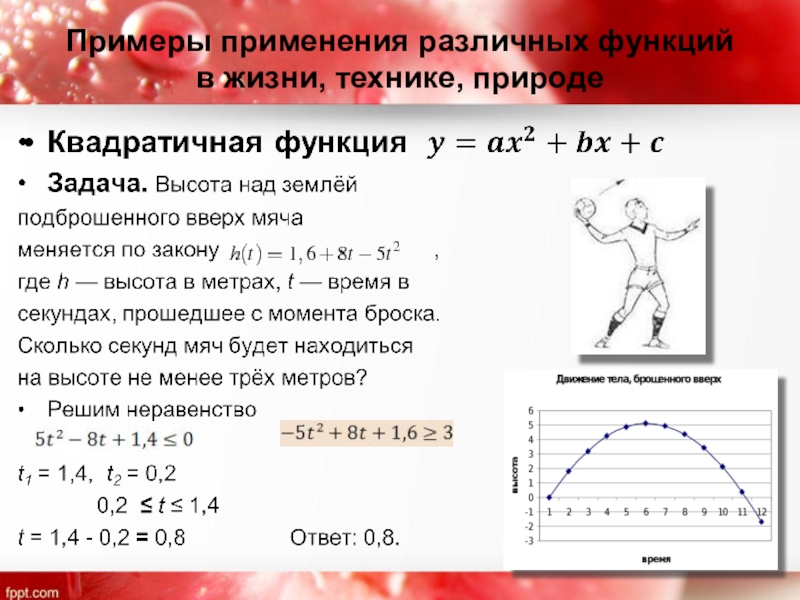
Слайд 27Примеры применения различных функций
в жизни, технике, природе
Тригонометрические функции
Задача. Невозможно представить жизнь
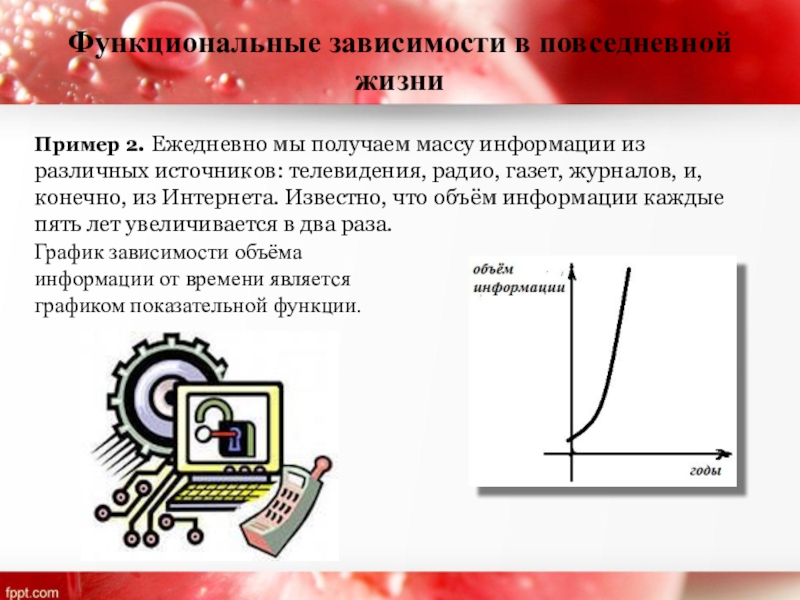
Слайд 29Функциональные зависимости в повседневной жизни
Пример 2. Ежедневно мы получаем массу информации
График зависимости объёма информации от времени является графиком показательной функции.
Слайд 30Функциональные зависимости в повседневной жизни
Изменение температурного режима в нашей климатической зоне
Яблоко росло, зрело, потом его высушили.
Слайд 31 Выводы:
Развития понятия функции не закончено. Новые открытия приведут к расширению
Функции служат «математическими портретами» законов природы и жизненных ситуаций.
Примеров функциональных зависимостей в повседневной жизни бесконечно много.
Слайд 32МАТЕМАТИКА И АВТОМОБИЛЬНАЯ ПРОМЫШЛЕННОСТЬ
ТРИГОНОМЕТРИЯ В ОКРУЖАЮЩЕМ НАС МИРЕ И В ЖИЗНИ
И АВТОМОБИЛЯ
ПРОБЛЕМНЫЙ ВОПРОС
1. КАКИЕ ПОНЯТИЯ ТРИГОНОМЕТРИИ ЧАЩЕ ВСЕГО ИСПОЛЬЗУЮТСЯ В РЕАЛЬНОЙ ЖИЗНИ?
2. КАКУЮ РОЛЬ ИГРАЕТ ТРИГОНОМЕТРИЯ В АВТОМОБИЛЬНОЙ ПРОМЫШЛЕННОСТИ, ФИЗИКЕ, БИОЛОГИИ И ХИМИИ?
3. КАК СВЯЗАНЫ АРХИТЕКТУРА АВТОМОБИЛЯ, МУЗЫКА В АВТОМОБИЛЕ И ТРИГОНОМЕТРИЯ?
Слайд 33История тригонометрии
По звездам вычисляли местонахождение корабля в море.
Древние люди
Истоки тригонометрии берут начало в древнем Египте, Вавилонии и долине Инда более 3000 лет назад.
Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом и Птолемеем.
Слайд 34
Сам термин косинус появился значительно позднее в работах европейских ученых
Слайд 36Стадии развития тригонометрии:
Тригонометрия была вызвана к жизни необходимостью производить измерения углов.
Первыми
Необходимость табулировать значения вводимых тригонометрических функций.
Тригонометрические функции превращались в самостоятельные объекты исследований.
В XVIII в. тригонометрические функции были включены в систему математического анализа.
Слайд 37Где применяется тригонометрия
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей.
Слайд 38Тригонометрия в физике
В окружающем нас мире приходится сталкиваться с периодическими процессами,
Механические колебания
Гармонические колебания
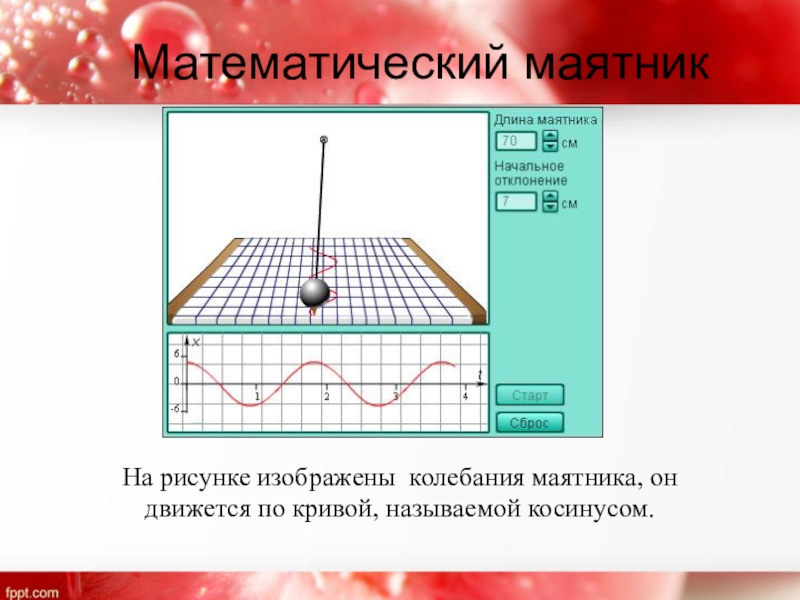
Слайд 39Математический маятник
На рисунке изображены колебания маятника, он движется по кривой, называемой
Слайд 40У музыки в автомобиле есть своя геометрия
Тетраэдр из различных типов аккордов
синий – малые интервалы;
более теплые тона - более «разряженные» звуки аккорда; красная сфера- наиболее гармоничный аккорд с равными интервалами между нотами.
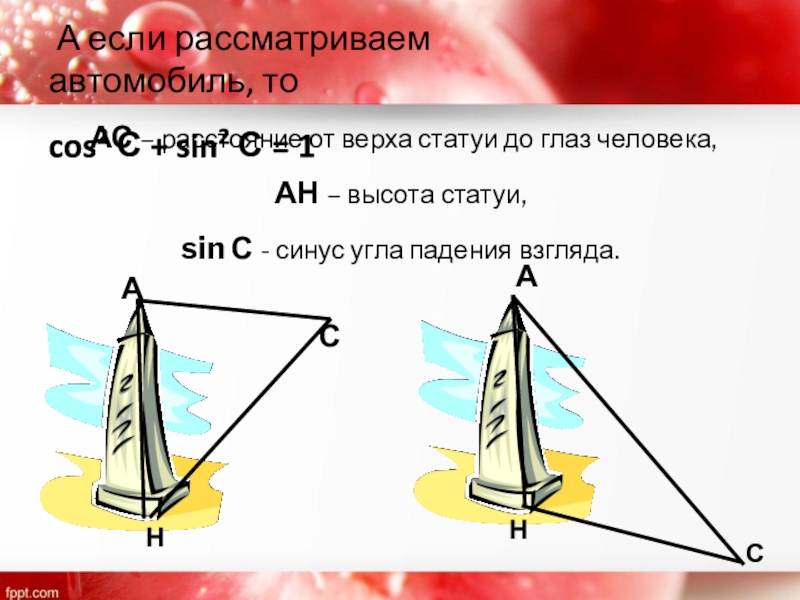
Слайд 41
С
А
Н
С
Н
А если рассматриваем автомобиль, то
cos2 С +
АС – расстояние от верха статуи до глаз человека,
АН – высота статуи,
sin С - синус угла падения взгляда.
А
Слайд 42Представьте, что вы припарковали автомобиль на стоянке у «Феликс Кандела» Ресторан в
[adcos(t) + ddt , bdsin(t), cdt + edt2]
Слайд 43Смотрим из окна автомобиля на звездное небо Тригонометрия в астрономии
Потребность в
Значительных высот достигла тригонометрия и у индийских средневековых астрономов.
Главным достижением индийских астрономов стала замена хорд
синусами, что позволило вводить различные функции, связанные
со сторонами и углами прямоугольного треугольника.
Таким образом, в Индии было положено начало тригонометрии
как учению о тригонометрических величинах.
Слайд 45Для технических профессий всегда необходимы задачи на движение, проценты, площади и
1) Два грузовика выехали в рейс по взаимно перпендикулярным дорогам. Скорость одного – 50 км/ч, скорость другого – 60 км/ч. В данный момент они находятся на расстоянии 7 км и 10 км от начала пути. Через какое время расстояние между ними будет 35 км?
Слайд 46Задача на расход бензина
2) Во время поездки автомобиль на каждые 100
Слайд 473) Сколько брезента необходимо для пошива тента для кузова автомобиля формы
3 х 1,50 х 2 м?
4) Сколько понадобится арматуры для изготовления каркаса кузова для автомобиля КАМАЗ, имеющего форму прямоугольного параллелепипеда с измерениями:
2 х 1,5 х 2?
Слайд 48Задачи на проценты
1) Автомеханик установил сначала 25% всех деталей машины при
2) Слесарь должен был изготовить определенное количество втулок, с нормой 19 втулок в день. Но он ежедневно изготавливал на 7 втулок больше, поэтому за 3 дня до срока он изготовил 29 втулок сверх плана. Сколько втулок сделал слесарь?
Слайд 49Площади и объёмы
1) Определить объём кузова автомобиля ГАЗ-53, если его длина
2) Вычислить объём дизтоплива в цистерне диаметром 2м и длиной 3м, если она заполнена на 2/3 объёма.
Слайд 50Вот такую работу мы проделали на кружке по математике «Математическое моделирование
СПАСИБО ЗА ВНИМАНИЕ!