- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по технической механике Общие теоремы динамики 2 курс ССУЗ
Содержание
- 1. Презентация по технической механике Общие теоремы динамики 2 курс ССУЗ
- 2. Цель урока:Обеспечение усвоения понятий импульса силы, количества
- 3. Любое взаимодействие тел, приводящее к какому-либо изменению
- 4. Если на точку действует несколько сил, то
- 5. Скалярная мера механического движения точки mv2/2, равная
- 6. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИПусть на
- 7. FΣ Δt = mV2—mV1Изменение количества движения точки
- 8. Пример1. Шофер автомобиля, движущегося со скоростью 60
- 9. Rf Δt = —mV1Спроецировав обе части равенства
- 10. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИПусть, как
- 11. При действии постоянных сил на прямолинейном пути:a
- 12. Если точка движется равномерно, т. е. V1=V2,
- 13. Пример 2. По условию примера 1 определить
- 14. ПОНЯТИЕ О МЕХАНИЧЕСКОЙ СИСТЕМЕСовокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.
- 15. Любое материальное тело рассматривается в механике как
- 16. Силы, действующие на точки системы со стороны
- 17. F12=-F21; F23=-F32, F31=-F13 Если рассматриваемая механическая система
- 18. Движение механической системы зависит не только от
Слайд 1Презентация по технической механике «Общие теоремы динамики»
Автор: преподаватель специальных дисциплин ГАПОУ
Слайд 2Цель урока:
Обеспечение усвоения понятий импульса силы, количества движения, кинетической энергии, механической
Способствовать формированию представлений об основных уравнениях динамики.
Способствовать формированию умений определять параметры движения с помощью теорем динамики.
Слайд 3Любое взаимодействие тел, приводящее к какому-либо изменению движения, длится в течение
Векторная мера действия силы Fdt, равная произведению силы на элементарный промежуток времени ее действия, называется элементарным импульсом силы.
Направление вектора импульса совпадает с направлением вектора силы.
Единица импульса в СИ — Н·с:
1 Н · с = 1 кг · м/с2 · 1 с = 1 кг · м/с
При F= const импульс силы за время Δt=t2—t1 равен
F Δt
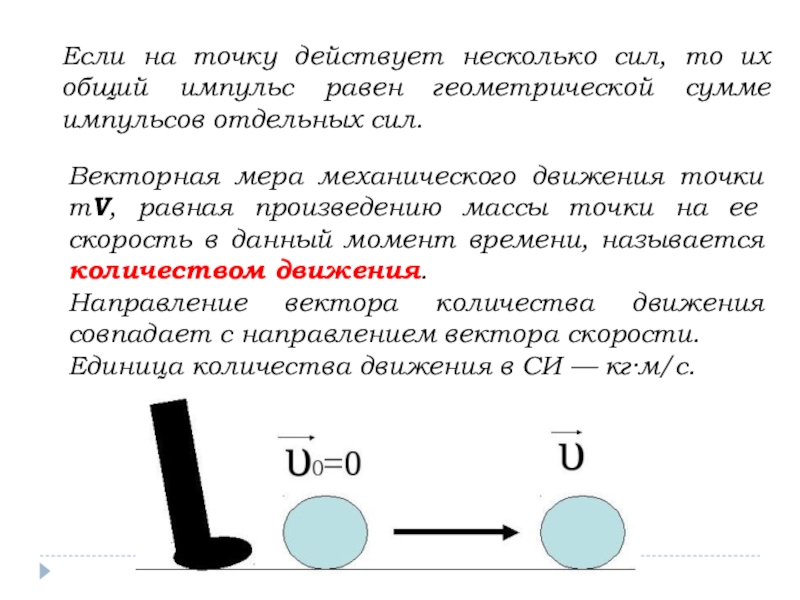
Слайд 4Если на точку действует несколько сил, то их общий импульс равен
Векторная мера механического движения точки mV, равная произведению массы точки на ее скорость в данный момент времени, называется количеством движения.
Направление вектора количества движения совпадает с направлением вектора скорости.
Единица количества движения в СИ — кг·м/с.
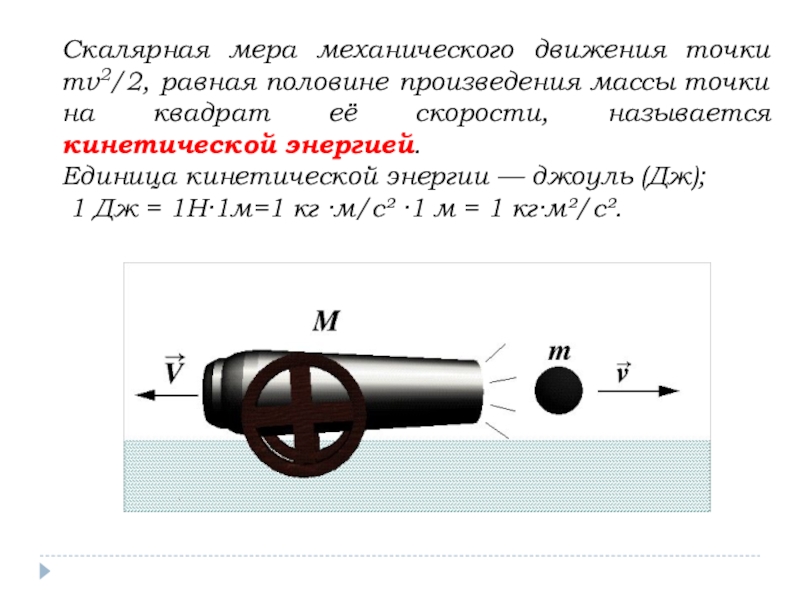
Слайд 5Скалярная мера механического движения точки mv2/2, равная половине произведения массы точки
Единица кинетической энергии — джоуль (Дж);
1 Дж = 1Н·1м=1 кг ·м/с² ·1 м = 1 кг·м²/с².
Слайд 6ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
Пусть на точку массой m действует
Согласно основному закону динамики:
FΣ = та
Учитывая время действия сил, умножим обе части равенства на продолжительность их действия Δt:
FΣ Δt = та Δt
a = (V2—V1)/(Δt)
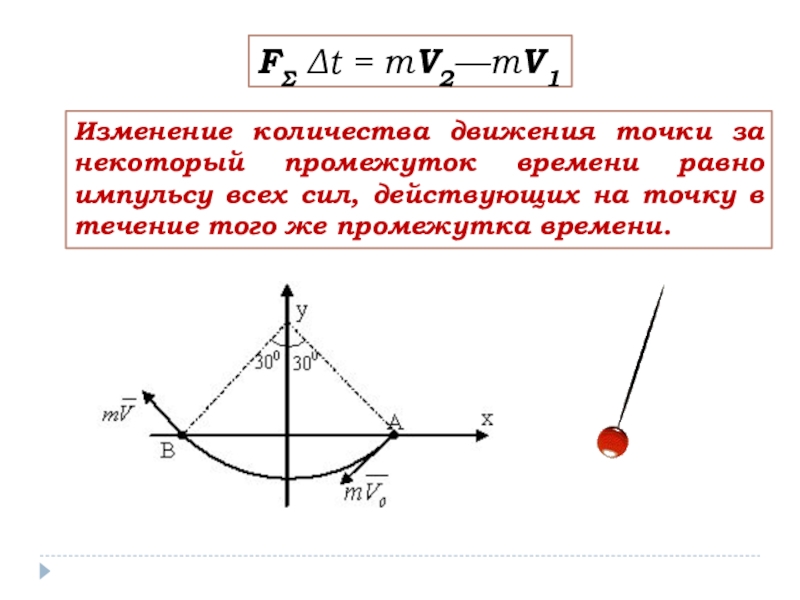
Слайд 7FΣ Δt = mV2—mV1
Изменение количества движения точки за некоторый промежуток времени
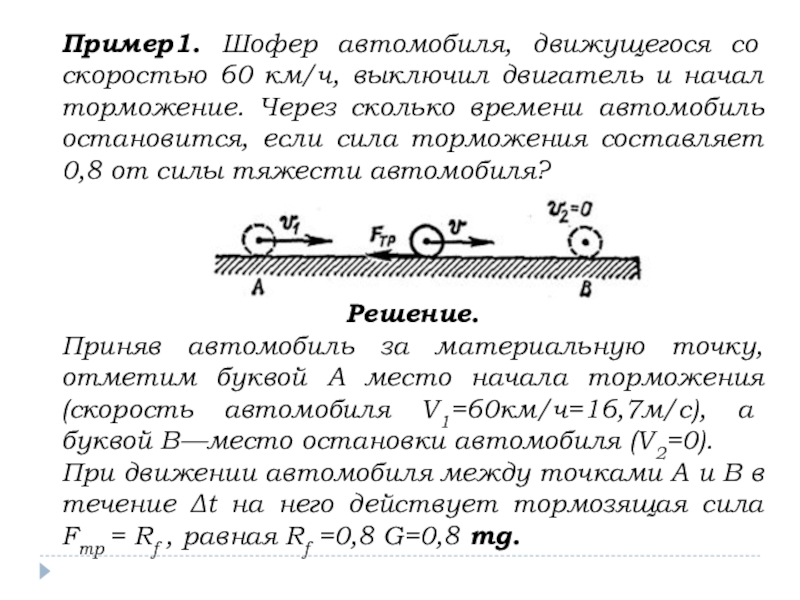
Слайд 8Пример1. Шофер автомобиля, движущегося со скоростью 60 км/ч, выключил двигатель и
Решение.
Приняв автомобиль за материальную точку, отметим буквой А место начала торможения (скорость автомобиля V1=60км/ч=16,7м/с), а буквой В—место остановки автомобиля (V2=0).
При движении автомобиля между точками А и В в течение Δt на него действует тормозящая сила Fтр = Rf , равная Rf =0,8 G=0,8 mg.
Слайд 9Rf Δt = —mV1
Спроецировав обе части равенства на ось, проходящую через
— Rf Δt =— mV1
Δt=mV1/Rf=mV1/(0,8mg)=16,7/(0,8·9,8)= = 2,13 с
Автомобиль остановится через 2,13 с.
Слайд 10ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
Пусть, как и в предыдущем случае,
Тогда основному закону динамики в векторной форме эквивалентно равенство:
FΣ = та
Умножим обе части этого равенства на перемещение точки ΔS:
FΣ ΔS = ma ΔS
Слайд 11При действии постоянных сил на прямолинейном пути:
a = (V2— V1)/Δt
ΔS = Vср Δt = (V2 + V1) Δt/2
FΣ ΔS = m[(V2— V1)/Δt][(V2 + V1)/Δt]/2
FΣ ΔS = WΣ = ΣWk
ΣWk = mV²2/2 — mV²1/2
Изменение кинетической энергии точки на некотором пути равно сумме работ всех действующих на точку сил на том же пути.
Слайд 12Если точка движется равномерно, т. е. V1=V2, и изменение кинетической энергии
ΣWk =0
Если V1>V2, то изменение кинетической энергии mV²2/2—mV²1/2>0, т. е. кинетическая энергия точки возрастает и, значит, работа движущих сил больше работ сил сопротивления.
Если V1
Слайд 13Пример 2. По условию примера 1 определить длину тормозного пути AB=S
Решение.
В соответствии с исходными данными уравнение кинетической энергии примет вид:
— Rf S = — mV²2/2
Отсюда, имея в виду, что Rf =0,8 mg, получим
S=mV²2/(2·0,8mg)=16,72/(2·0,8·9,8)≈17м
Тормозной путь составит 17 м.
Слайд 14ПОНЯТИЕ О МЕХАНИЧЕСКОЙ СИСТЕМЕ
Совокупность материальных точек, связанных между собой силами взаимодействия,
Слайд 15Любое материальное тело рассматривается в механике как механическая система, образуемая совокупностью
Абсолютно твердое тело называется неизменяемой механической системой, так как расстояние между материальными точками остается неизменным.
Механические системы, расстояния между точками которых могут меняться, называются изменяемыми. К ним относятся любые машины или механизмы.
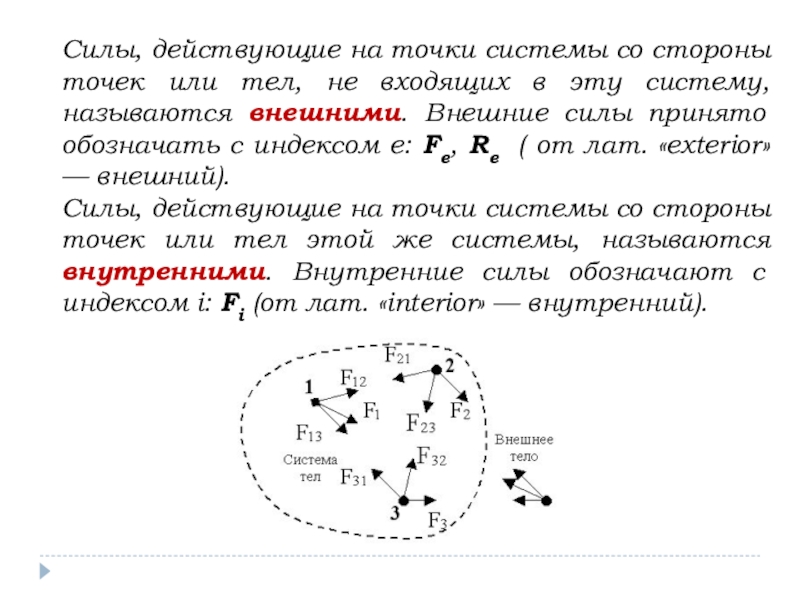
Слайд 16Силы, действующие на точки системы со стороны точек или тел, не
Силы, действующие на точки системы со стороны точек или тел этой же системы, называются внутренними. Внутренние силы обозначают с индексом i: Fi (от лат. «interior» — внутренний).
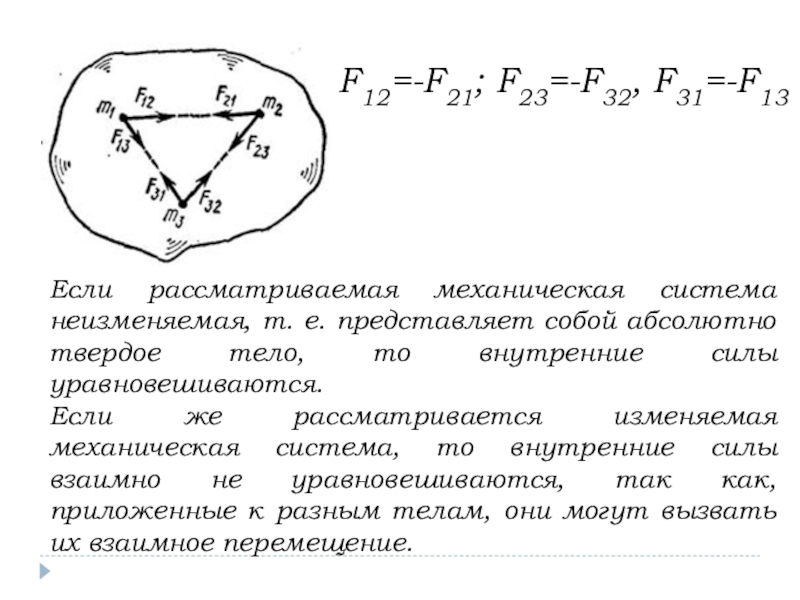
Слайд 17F12=-F21; F23=-F32, F31=-F13
Если рассматриваемая механическая система неизменяемая, т. е. представляет
Если же рассматривается изменяемая механическая система, то внутренние силы взаимно не уравновешиваются, так как, приложенные к разным телам, они могут вызвать их взаимное перемещение.
Слайд 18Движение механической системы зависит не только от действующих сил, оно зависит
m = ΣΔmk
где m — масса механической системы
и Δmk — массы ее отдельных точек,
и, во-вторых, от положения центра масс системы.
Движение центра масс определяется уравнением:
FeΣ S = mac
где FeΣ — результирующая всех внешних сил, приложенных к точкам системы;
m — масса системы;
ac — ускорение центра масс системы.