Презентация, доклад по основам теории информации на тему Энтропия и информация

Содержание

1. Презентация по основам теории информации на тему Энтропия и информация
2. Случайные события. Мера их неопределенности. Формула Хартли.
3. Степень неопределенности – есть еще одна характеристика
4. Формула ХартлиПусть опыт α имеет k равновозможных исходов, тогда Этой формулой удобно пользоваться, когда исходы равновероятны.
5. Чем больше равновероятных исходов, тем больше степень
6. Энтропия по Шеннону. Свойства энтропии.
7. Где
8. Имеются 2 урны. Первая содержит 20
9. Какую степень неопределенности содержит опыт угадывания цвета
10. Условная энтропия. Решение задач на условную энтропию.
11. Граф и формула нахождения условной энтропии выглядит
12. Какую энтропию содержит опыт угадывания простой цифры
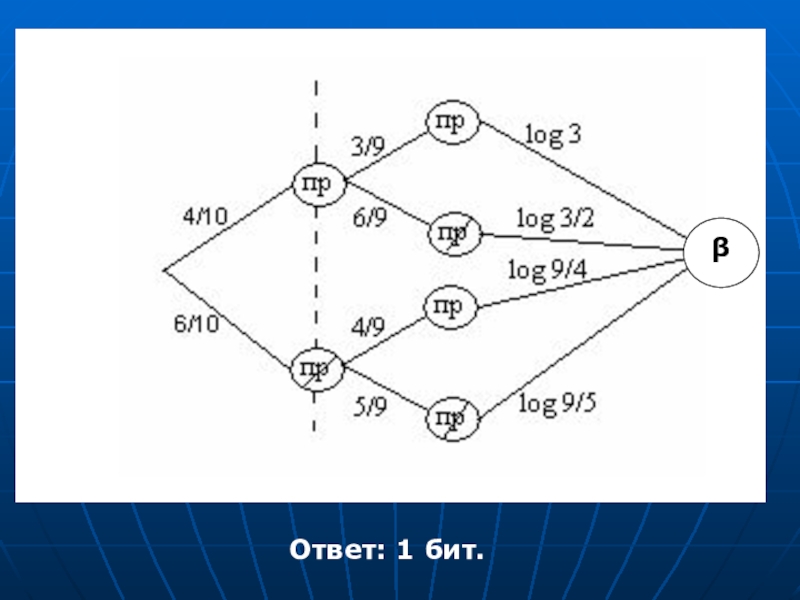
13. βОтвет: 1 бит.
14. Количество информации. Решение задач
15. КОЛИЧЕСТВО ИНФОРМАЦИИ Количество информации I(α,β) показывает,
16. Свойства количества информации0 ≤I(β/α) ≤ Н(β)I(α,β) =
17. Решение логических задач на взвешивание через энтропию и количество информации.
18. ЗАДАЧИ НА ВЗВЕШИВАНИЕЗадача: Имеется 12
19. Решение:т.е. определение фальшивой монеты связано с получением
20. M1 M2 M3 M4M5 M6 M7 M8M9

Случайные события. Мера их неопределенности. Формула Хартли.

Главная
Разное
Презентация по основам теории информации на тему Энтропия и информация

Слайд 1«Энтропия и информация»

Слайд 2Случайные события. Мера их неопределенности. Формула Хартли.

Слайд 3 Степень неопределенности – есть еще одна характеристика случайного события, которую назвали

энтропией. (Н(α)).

За единицу энтропии принимается неопределенность, содержащаяся в опыте, имеющем два равновероятностных исхода.

Единица измерения, учитывая двоичную систему исчисления, - бит.

Степень неопределенности – есть еще одна характеристика случайного события, которую назвали энтропией. (Н(α)). За единицу энтропии принимается

Слайд 4Формула Хартли
Пусть опыт α имеет k равновозможных исходов, тогда

Этой

формулой удобно пользоваться, когда исходы равновероятны.

Слайд 5Чем больше равновероятных исходов, тем больше степень неопределенности
Чем меньше вероятность, тем

больше степень неопределенности

Что имеет большую степень неопределенности угадывание месяца или дня недели рождения случайно встреченного человека?

Какую степень неопределенности имеет угадывание месяца рождения случайно встреченного человека?
Н(α) = log k = log12 = 2 + log 3.

Чем больше равновероятных исходов, тем больше степень неопределенностиЧем меньше вероятность, тем больше степень неопределенностиЧто имеет большую степень

Слайд 6Энтропия по Шеннону. Свойства энтропии.

Слайд 7Где

вероятности равновозможных исходов.
Он же предложил назвать эту величину энтропией

Клод Шеннон

Слайд 8Имеются 2 урны. Первая содержит 20 шаров – 10 белых, 5

черных и 5 красных; Вторая содержит 16 шаров: 4 белых, 4 черных и 8 красных во второй. Из каждой урны вытаскивают по одному шару. Исход какого из этих двух опытов следует считать более неопределенным?

Первый опыт связан с первой корзиной:
Н (α)= -1\2 log 1\2 - 1\4 log 1\4 - 1\4 log 1\4 = 1\2 +1\2 +1\2 = 3\2 бита

Второй опыт связан со второй корзиной:
Н (β)= -1\2 log 1\2 - 1\4 log 1\4 - 1\4 log 1\4 = 1\2 +1\2 +1\2 = 3\2 бита

Имеются 2 урны. Первая содержит 20 шаров – 10 белых, 5 черных и 5 красных;

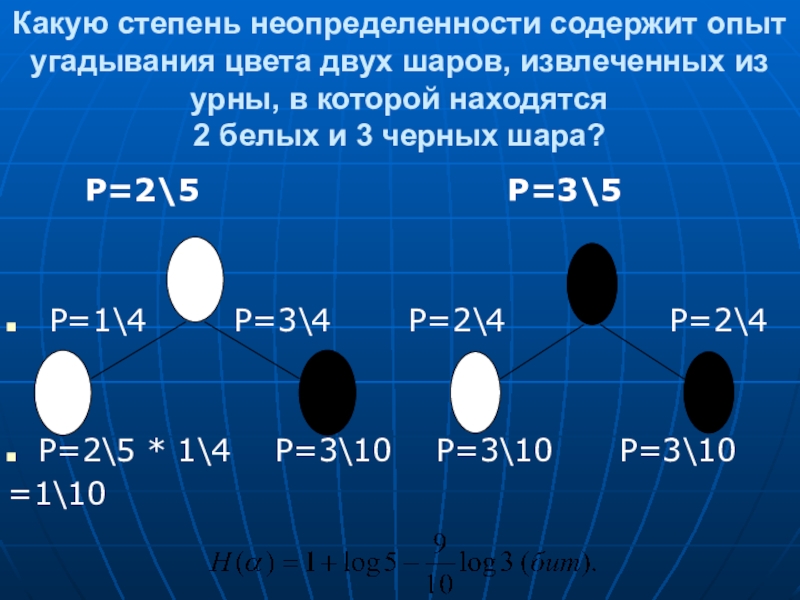
Слайд 9Какую степень неопределенности содержит опыт угадывания цвета двух шаров, извлеченных из

урны, в которой находятся 2 белых и 3 черных шара?

Р=2\5 Р=3\5

Р=1\4 Р=3\4 Р=2\4 Р=2\4

Р=2\5 * 1\4 Р=3\10 Р=3\10 Р=3\10
=1\10

Какую степень неопределенности содержит опыт угадывания цвета двух шаров, извлеченных из урны, в которой находятся 2

Слайд 10Условная энтропия. Решение задач на условную энтропию.

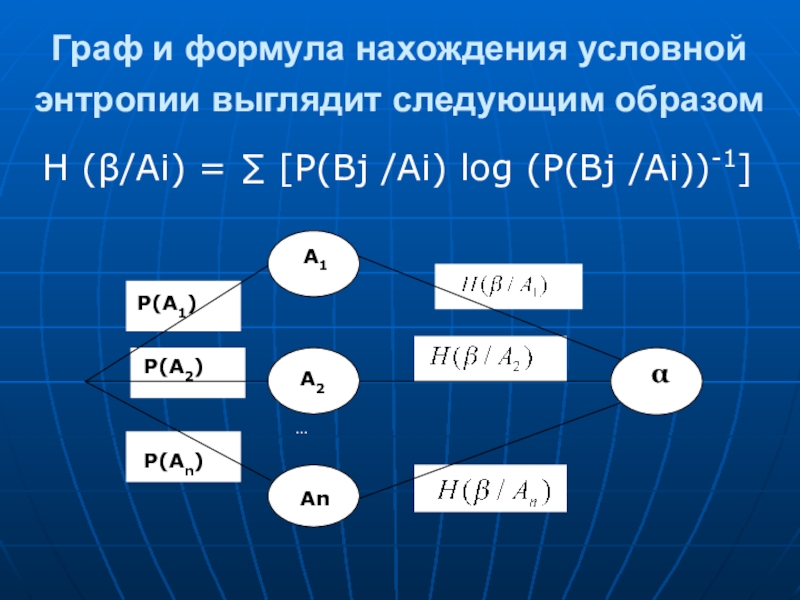
Слайд 11Граф и формула нахождения условной энтропии выглядит следующим образом
Н (β/Аi)

= ∑ [Р(Вj /Аi) log (Р(Вj /Аi))-1]

P(A2)

P(A1)

P(An)

Граф и формула нахождения условной энтропии выглядит следующим образом Н (β/Аi) = ∑ [Р(Вj /Аi) log (Р(Вj

Слайд 12Какую энтропию содержит опыт угадывания простой цифры при извлечении из цифровой

азбуки при условии, что одна карточка утеряна?

Опыт α = {утеряна одна карточка} = {А1, А2 }

А1 = {утеряна карточка с простой цифрой}, n(А1) = 4, Р(А1)= 4/10 =2/5,

А2 = {утеряна карточка с непростой цифрой}, n(А2) = 6, Р(А2)= 6 /10 =3/5

β = {угадывание карточки с простой цифрой}

Какую энтропию содержит опыт угадывания простой цифры при извлечении из цифровой азбуки при условии, что одна карточка

Слайд 13 β
Ответ: 1 бит.

Слайд 14Количество информации. Решение задач

Слайд 15КОЛИЧЕСТВО ИНФОРМАЦИИ

Количество информации I(α,β) показывает, насколько осуществление опыта α

уменьшает неопределенность β т.е. как много нового узнаем мы об исходе опыта β, произведя измерение (наблюдение) α;

Информацию можно измерить числом, которое называется количеством информации об опыте β, содержащемся в опыте α

I(α,β)=H(β) – H(β/α)

КОЛИЧЕСТВО ИНФОРМАЦИИ Количество информации I(α,β) показывает, насколько осуществление опыта α уменьшает неопределенность β т.е. как много

Слайд 16Свойства количества информации

0 ≤I(β/α) ≤ Н(β)
I(α,β) = Н(α) + Н(β) -

Н(α*β),
I(α,β) = I(β,α)
I(α,β,γ) ≥I(α,β), где α,β,γ- три произвольных опыта

Свойства количества информации0 ≤I(β/α) ≤ Н(β)I(α,β) = Н(α) + Н(β) - Н(α*β),I(α,β) = I(β,α)I(α,β,γ) ≥I(α,β), где α,β,γ-

Слайд 17Решение логических задач на взвешивание через энтропию и количество информации.

Слайд 18ЗАДАЧИ НА ВЗВЕШИВАНИЕ
Задача:
Имеется 12 монет одного достоинства, одна

из которых фальшивая, отличающаяся от других по весу (причем неизвестно, легче она или тяжелее настоящих).

Каково наименьшее число взвешиваний на чашечных весах без гирь, которое позволяет обнаружить фальшивую монету?

ЗАДАЧИ НА ВЗВЕШИВАНИЕЗадача: Имеется 12 монет одного достоинства, одна из которых фальшивая, отличающаяся от других

Слайд 19Решение:
т.е. определение фальшивой монеты связано с получением информации, измеряющейся числом log24
или

k*log3≥log24

Отсюда и
т.к. k – целое число, то k≥3

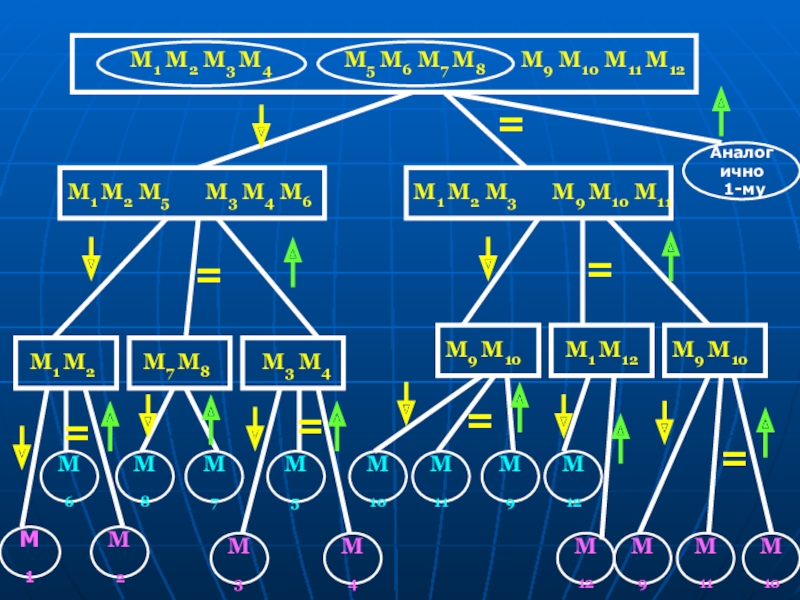
Слайд 20
M1 M2 M3 M4
M5 M6 M7 M8
M9 M10 M11 M12

=

M3 M4

M1 M2 M5

М1

М2

М7

М5

М8

М3

М4

М11

М10

М6

М12

М9

М10

М11

М9

М12

Аналогично
1-му

M1 M2

M7 M8

M3 M4

M1 M2 M3

M9 M10 M11

M9 M10

M1 M12

M9 M10

Скачать презентацию

Презентация, доклад по основам теории информации на тему Энтропия и информация

Содержание

Слайд 1«Энтропия и информация»

Слайд 2Случайные события. Мера их неопределенности. Формула Хартли.

Слайд 3 Степень неопределенности – есть еще одна характеристика случайного события, которую назвали

Слайд 4Формула Хартли
Пусть опыт α имеет k равновозможных исходов, тогда

Этой

Слайд 5Чем больше равновероятных исходов, тем больше степень неопределенности
Чем меньше вероятность, тем

Слайд 6Энтропия по Шеннону. Свойства энтропии.

Слайд 7Где

Слайд 8Имеются 2 урны. Первая содержит 20 шаров – 10 белых, 5

Слайд 9Какую степень неопределенности содержит опыт угадывания цвета двух шаров, извлеченных из

Слайд 10Условная энтропия. Решение задач на условную энтропию.

Слайд 11Граф и формула нахождения условной энтропии выглядит следующим образом
Н (β/Аi)

Слайд 12Какую энтропию содержит опыт угадывания простой цифры при извлечении из цифровой

Слайд 13 β
Ответ: 1 бит.

Слайд 14Количество информации. Решение задач

Слайд 15КОЛИЧЕСТВО ИНФОРМАЦИИ

Количество информации I(α,β) показывает, насколько осуществление опыта α

Слайд 16Свойства количества информации

0 ≤I(β/α) ≤ Н(β)
I(α,β) = Н(α) + Н(β) -

Слайд 17Решение логических задач на взвешивание через энтропию и количество информации.

Слайд 18ЗАДАЧИ НА ВЗВЕШИВАНИЕ
Задача:
Имеется 12 монет одного достоинства, одна

Слайд 19Решение:
т.е. определение фальшивой монеты связано с получением информации, измеряющейся числом log24
или

Слайд 20
M1 M2 M3 M4
M5 M6 M7 M8
M9 M10 M11 M12

=

M3 M4

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по основам теории информации на тему Энтропия и информация

Содержание

Слайд 1«Энтропия и информация»

Слайд 2Случайные события. Мера их неопределенности. Формула Хартли.

Слайд 3 Степень неопределенности – есть еще одна характеристика случайного события, которую назвали

Слайд 4Формула ХартлиПусть опыт α имеет k равновозможных исходов, тогда Этой

Слайд 5Чем больше равновероятных исходов, тем больше степень неопределенностиЧем меньше вероятность, тем

Слайд 6Энтропия по Шеннону. Свойства энтропии.

Слайд 7Где

Слайд 8Имеются 2 урны. Первая содержит 20 шаров – 10 белых, 5

Слайд 9Какую степень неопределенности содержит опыт угадывания цвета двух шаров, извлеченных из

Слайд 10Условная энтропия. Решение задач на условную энтропию.

Слайд 11Граф и формула нахождения условной энтропии выглядит следующим образом Н (β/Аi)

Слайд 12Какую энтропию содержит опыт угадывания простой цифры при извлечении из цифровой

Слайд 13 βОтвет: 1 бит.

Слайд 14Количество информации. Решение задач

Слайд 15КОЛИЧЕСТВО ИНФОРМАЦИИ Количество информации I(α,β) показывает, насколько осуществление опыта α

Слайд 16Свойства количества информации0 ≤I(β/α) ≤ Н(β)I(α,β) = Н(α) + Н(β) -

Слайд 17Решение логических задач на взвешивание через энтропию и количество информации.

Слайд 18ЗАДАЧИ НА ВЗВЕШИВАНИЕЗадача: Имеется 12 монет одного достоинства, одна

Слайд 19Решение:т.е. определение фальшивой монеты связано с получением информации, измеряющейся числом log24или

Слайд 20M1 M2 M3 M4M5 M6 M7 M8M9 M10 M11 M12=M3 M4

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 4Формула Хартли
Пусть опыт α имеет k равновозможных исходов, тогда

Этой

Слайд 5Чем больше равновероятных исходов, тем больше степень неопределенности
Чем меньше вероятность, тем

Слайд 11Граф и формула нахождения условной энтропии выглядит следующим образом
Н (β/Аi)

Слайд 13 β
Ответ: 1 бит.

Слайд 15КОЛИЧЕСТВО ИНФОРМАЦИИ

Количество информации I(α,β) показывает, насколько осуществление опыта α

Слайд 16Свойства количества информации

0 ≤I(β/α) ≤ Н(β)
I(α,β) = Н(α) + Н(β) -

Слайд 18ЗАДАЧИ НА ВЗВЕШИВАНИЕ
Задача:
Имеется 12 монет одного достоинства, одна

Слайд 19Решение:
т.е. определение фальшивой монеты связано с получением информации, измеряющейся числом log24
или

Слайд 20
M1 M2 M3 M4
M5 M6 M7 M8
M9 M10 M11 M12

=

M3 M4