и его свойства. Маршрут, путь и цикл.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Графы 5-7 классы разработка внеурочного занятия
Содержание
- 1. Презентация по математике Графы 5-7 классы разработка внеурочного занятия
- 2. ЗадачаВ 10 – значном числе каждые две
- 3. Решать некоторые математические задачи помогают
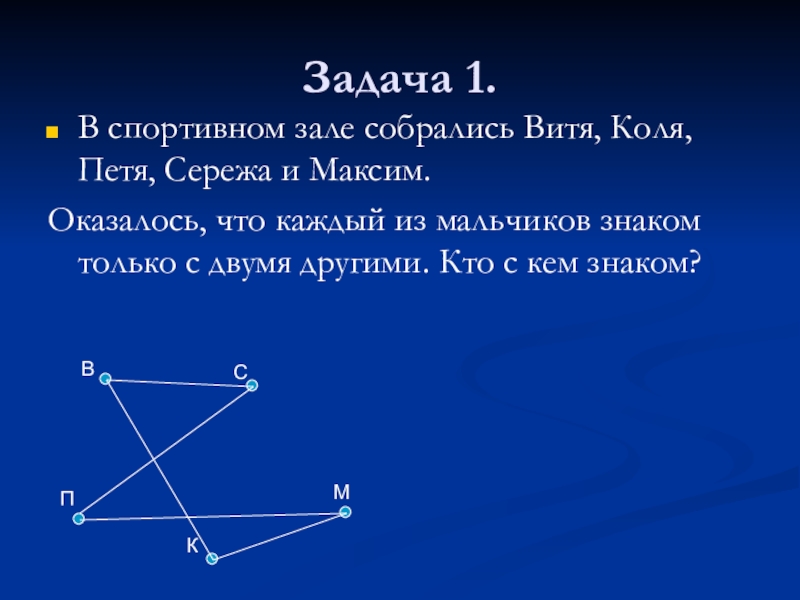
- 4. Задача 1.В спортивном зале собрались Витя, Коля,
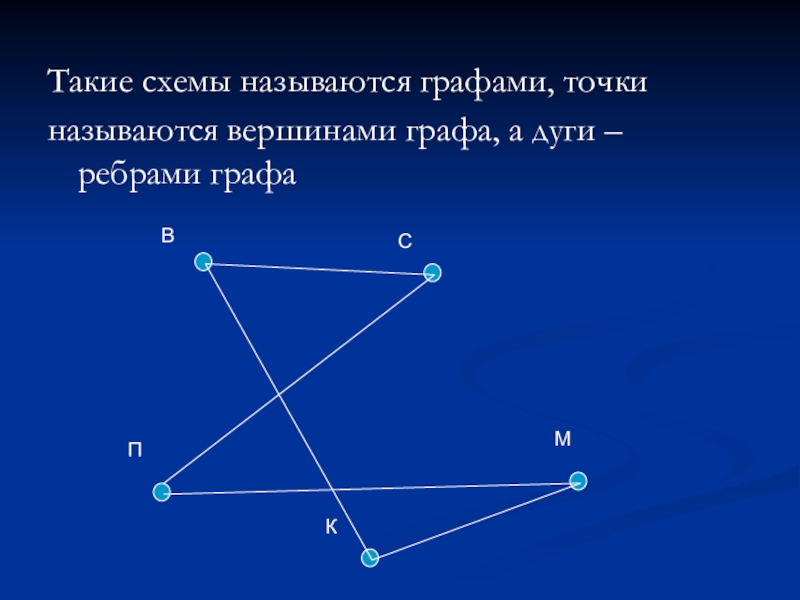
- 5. Такие схемы называются графами, точки называются вершинами графа, а дуги – ребрами графа
- 6. Примеры различных графов
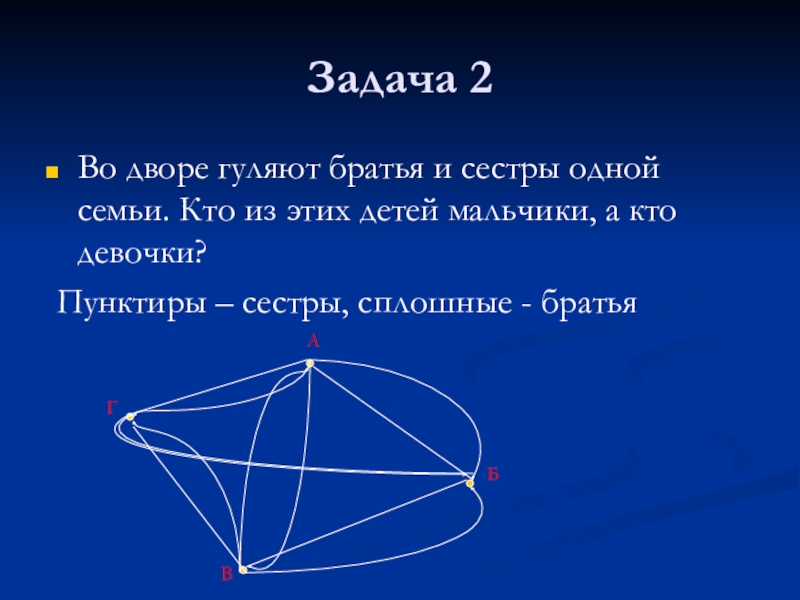
- 7. Задача 2Во дворе гуляют братья и сестры
- 8. Задача 3В Государстве Морляндии 8 крупных островов,
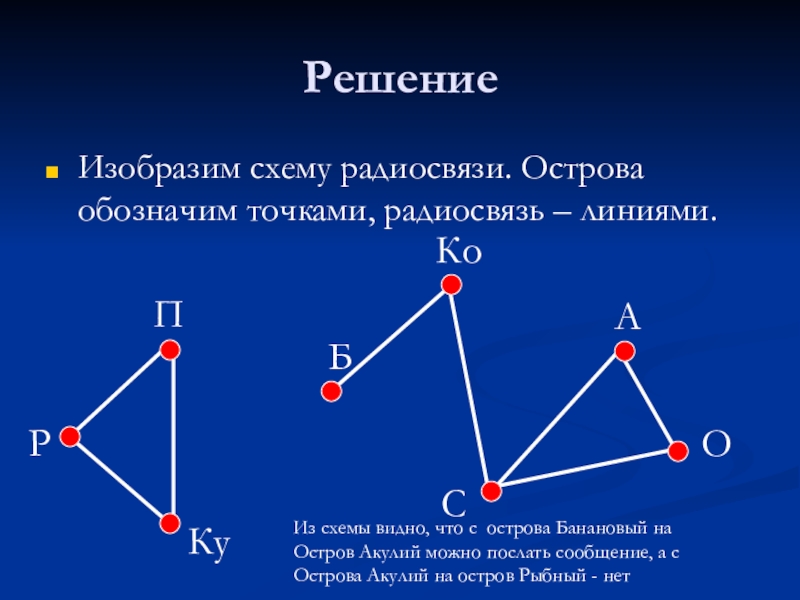
- 9. РешениеИзобразим схему радиосвязи. Острова обозначим точками, радиосвязь
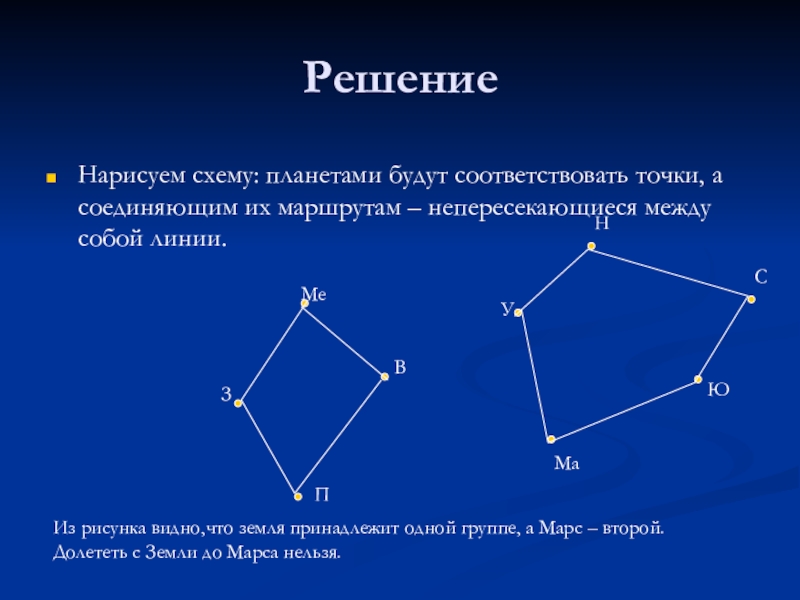
- 10. Задача 4Между 9 планетами Солнечной системы введено
- 11. РешениеНарисуем схему: планетами будут соответствовать точки, а
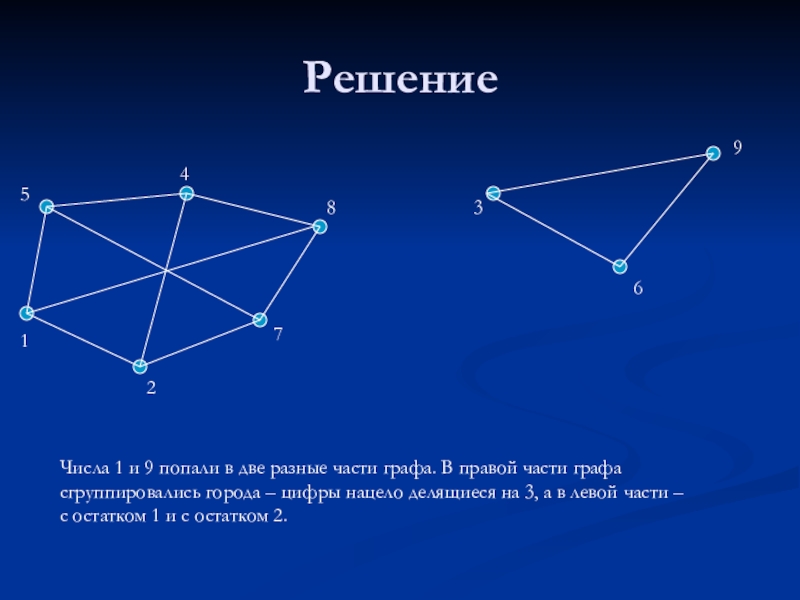
- 12. Задача 5В стране Цифра есть 9 городов
- 13. Решение154872396Числа 1 и 9 попали в две
- 14. Графы могут быть изображены по разному. Можно
- 15. ЗадачаВ 10 – значном числе каждые две
- 16. РешениеДвузначные числа, которые делятся на 13: 13;
- 17. Если линия имеет направление, она называется дугой,
- 18. Пара вершин графа может соединяться двумя или
- 19. Ребро (или дуга) может начинаться и заканчиваться в одной вершине, такое ребро называется петлей
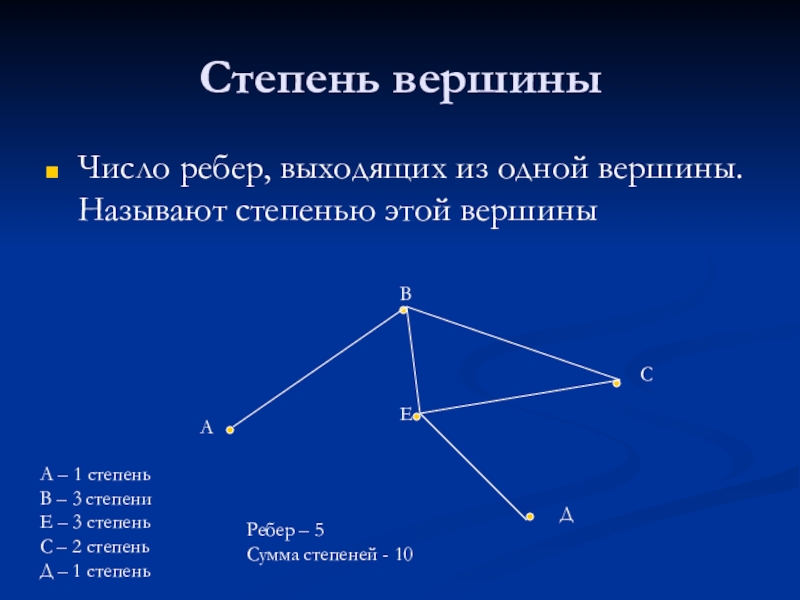
- 20. Степень вершиныЧисло ребер, выходящих из одной вершины.
- 21. Лемма 1Число ребер в графе ровно в
- 22. Задача 6 В деревне 10 домов, и
- 23. Лемма 2Сумма степеней вершин графа четна.Это утверждение
- 24. Задача 7Между семью планетами звездной системы установлено
- 25. РешениеПусть планеты – вершины графа – вершины
- 26. Если степень вершины четная, то вершина называется четной, если степень нечетная, то вершина нечетная.
- 27. Лемма 3Число нечетных вершин графа четно.Если в
- 28. Задача 8Маша сказала своей подружке Лене:«У нас
- 29. РешениеПредставим, что между каждыми двумя друзьями протянута
- 30. Задача 9Можно ли найти 5 натуральных чисел,
- 31. РешениеПредставим. Что мы нашли такие числа. Пусть
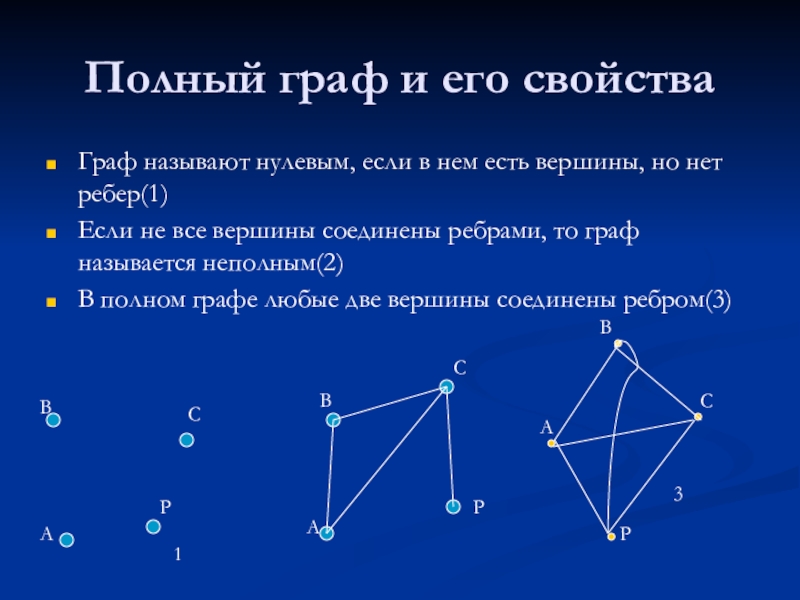
- 32. Полный граф и его свойстваГраф называют нулевым,
- 33. Лемма 4В полном графе с n вершинами
- 34. Задача 10Сколько диагоналей в 17 – угольнике?
- 35. РешениеВершины 17 – ти угольника – вершины
- 36. Задача 11Ваня и Миша играют в такую
- 37. РешениеПосле того как все ленты будут завязаны,
- 38. Задача 12В сарае 10 корыт с едой
- 39. РешениеОбозначим корыта точками- вершинами графа. Если между
- 40. Путь, маршрут и цикл в графеМаршрутом в
- 41. Путем(или цепью) в графе называется маршрут, в
- 42. ЗадачаНа рисунке изображены расстояния между пунктами А,
- 43. РешениеРассмотрим последовательно возможные пути поездки и сравним
ЗадачаВ 10 – значном числе каждые две подряд идущие цифры образуют двузначное число, которое делится на 13. Докажите, что среди этих цифр нет цифры 8.
Слайд 1
Внеурочная деятельность
Тема:
«Графы»
1 занятие
Основные понятия теории графов. Степень вершины. Полный граф
Слайд 2Задача
В 10 – значном числе каждые две подряд идущие цифры образуют
двузначное число, которое делится на 13. Докажите, что среди этих цифр нет цифры 8.
Слайд 3 Решать некоторые математические задачи помогают специальные схемы, состоящие из
точек и соединяющих их дуг или стрелок
Слайд 4Задача 1.
В спортивном зале собрались Витя, Коля, Петя, Сережа и Максим.
Оказалось,
что каждый из мальчиков знаком только с двумя другими. Кто с кем знаком?
Слайд 7Задача 2
Во дворе гуляют братья и сестры одной семьи. Кто из
этих детей мальчики, а кто девочки?
Пунктиры – сестры, сплошные - братья
Пунктиры – сестры, сплошные - братья
Г
А
Б
В
Слайд 8Задача 3
В Государстве Морляндии 8 крупных островов, между некоторыми из них
налажена радиосвязь. Связь есть между следующими островами: Банановый – Кокосовый, Кукуру – Рыбный, Столичный – Акулий, Птичий –Кукуру, Одинокий – Столичный, Акулий – Одинокий, Столичный – Кокосовый, Птичий – Рыбный. Можно ли послать сообщение с острова Банановый на остров Акулий?
А с острова Акулий на Рыбный?
А с острова Акулий на Рыбный?
Слайд 9Решение
Изобразим схему радиосвязи. Острова обозначим точками, радиосвязь – линиями.
Р
П
Ку
С
Из схемы видно,
что с острова Банановый на
Остров Акулий можно послать сообщение, а с
Острова Акулий на остров Рыбный - нет
Остров Акулий можно послать сообщение, а с
Острова Акулий на остров Рыбный - нет
Слайд 10Задача 4
Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают
по следующим маршрутам: Земля – Меркурий, Плутон – Венера, Земля – Плутон, Плутон – Меркурий, Меркурий – Венера, Уран – Нептун, Нептун – Сатурн, Сатурн – Юпитер, Юпитер – Марс и Марс – Уран.
Можно ли добраться (возможны пересадки) с Земли до Марса?
Можно ли добраться (возможны пересадки) с Земли до Марса?
Слайд 11Решение
Нарисуем схему: планетами будут соответствовать точки, а соединяющим их маршрутам –
непересекающиеся между собой линии.
Ме
Из рисунка видно,что земля принадлежит одной группе, а Марс – второй.
Долететь с Земли до Марса нельзя.
Слайд 12Задача 5
В стране Цифра есть 9 городов с названиями 1, 2,
3, 4, 5, 6 ,7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией тогда и только тогда, когда двузначное число, составленное из цифр – названий этих городов, делится на 3. Можно ли из города 1 добраться в город 9?
Слайд 13Решение
1
5
4
8
7
2
3
9
6
Числа 1 и 9 попали в две разные части графа. В
правой части графа
сгруппировались города – цифры нацело делящиеся на 3, а в левой части –
с остатком 1 и с остатком 2.
сгруппировались города – цифры нацело делящиеся на 3, а в левой части –
с остатком 1 и с остатком 2.
Слайд 14Графы могут быть изображены по разному. Можно получить столько разных графов,
сколько учеников в классе.
Нарисованные по – разному графы(если они нарисованы без ошибок) принято называть изоморфными
Нарисованные по – разному графы(если они нарисованы без ошибок) принято называть изоморфными
Слайд 15Задача
В 10 – значном числе каждые две подряд идущие цифры образуют
двузначное число, которое делится на 13. Докажите, что среди этих цифр нет цифры 8.
Слайд 16Решение
Двузначные числа, которые делятся на 13: 13; 26; 39; 52; 65;
78; 91.
13
39
91
78
65
52
26
Видно, что если 10 – значное число обладает заданным свойством, то оно
состоит из периодически повторяющихся цифр … 1391…или …6526…
Цифры 8 быть не может
Слайд 17Если линия имеет направление, она называется дугой, а граф, содержащий только
дуги – ориентированным.
Вершины, соединенные ребром, называют смежными.
Ребра, имеющие общую вершину, тоже называют смежными.
Вершины, соединенные ребром, называют смежными.
Ребра, имеющие общую вершину, тоже называют смежными.
Слайд 18Пара вершин графа может соединяться двумя или более ребрами (или дугами
одинакового направления, если граф ориентированный), тогда они называются кратными.
Слайд 19Ребро (или дуга) может начинаться и заканчиваться в одной вершине, такое
ребро называется петлей
Слайд 20Степень вершины
Число ребер, выходящих из одной вершины. Называют степенью этой вершины
А
В
С
Е
Д
А
– 1 степень
В – 3 степени
Е – 3 степень
С – 2 степень
Д – 1 степень
В – 3 степени
Е – 3 степень
С – 2 степень
Д – 1 степень
Ребер – 5
Сумма степеней - 10
Слайд 21Лемма 1
Число ребер в графе ровно в два раза меньше, чем
сумма степеней вершин
Доказательство:
Любое ребро графа связывает две вершины. Значит, если будем складывать число степеней всех вершин графа, то получим удвоенное число ребер, т. к. каждое ребро было подсчитано дважды.
Доказательство:
Любое ребро графа связывает две вершины. Значит, если будем складывать число степеней всех вершин графа, то получим удвоенное число ребер, т. к. каждое ребро было подсчитано дважды.
Слайд 22Задача 6
В деревне 10 домов, и из каждого выходит по
7 тропинок, идущих к другим домам. Сколько всего тропинок проходит между домами?
Решение: Пусть дома – вершины графа, тропинки – ребра. Тогда степень каждой вершины равна 7. Домов 10. Значит сумма степеней равна 70, тогда число ребер (тропинок) равна 35 (70 : 2)
Решение: Пусть дома – вершины графа, тропинки – ребра. Тогда степень каждой вершины равна 7. Домов 10. Значит сумма степеней равна 70, тогда число ребер (тропинок) равна 35 (70 : 2)
Слайд 23Лемма 2
Сумма степеней вершин графа четна.
Это утверждение становится понятным, если вспомнить
, что по лемме 1 эта сумма равна удвоенному количеству ребер.
Слайд 24Задача 7
Между семью планетами звездной системы установлено ракетное сообщение. Министр отрапортовал,
что с каждой планеты существует прямой рейс ровно на 5 других планет системы.
Докажите , что министр ошибся.
Докажите , что министр ошибся.
Слайд 25Решение
Пусть планеты – вершины графа – вершины графа, а маршруты –
ребра. Если министр прав, то сумма степеней вершин этого графа равна 7*5 = 35, а нечетной сумма степеней быть не может. Значит министр ошибся.
Слайд 26Если степень вершины четная, то вершина называется четной, если степень нечетная,
то вершина нечетная.
Слайд 27Лемма 3
Число нечетных вершин графа четно.
Если в графе есть n четных
и k нечетных вершин, то сумма степеней четных вершин четна как сумма четных чисел. Сумма степеней нечетных вершин нечетна, если их количество k
нечетно. Но тогда общее число степеней
вершин тоже нечетно, чего не может быть.
Значит k четно.
нечетно. Но тогда общее число степеней
вершин тоже нечетно, чего не может быть.
Значит k четно.
Слайд 28Задача 8
Маша сказала своей подружке Лене:
«У нас в классе 25 человек.
И представь, каждый из них дружит ровно с семью одноклассниками». «Не может этого быть» - ответила Лена.
Слайд 29Решение
Представим, что между каждыми двумя друзьями протянута веревочка. Значит у протянутых
веревочек будет 25*7 = 175
концов. Но их общее число концов не может быть нечетным, так как у каждой веревочки 2 конца.
концов. Но их общее число концов не может быть нечетным, так как у каждой веревочки 2 конца.
Слайд 30Задача 9
Можно ли найти 5 натуральных чисел, таких, что для каждого
из них среди оставшихся чисел найдется ровно три числа с одинаковым простым делителем?
Слайд 31Решение
Представим. Что мы нашли такие числа.
Пусть эти числа будут вершинами
графа. Если два числа имеют одинаковый простой делитель, соединим их ребром. Степень каждой вершины такого графа равна 3, вершин 5. Но в графе не может быть нечетного числа нечетных вершин.
Значит, такие числа найти нельзя.
Значит, такие числа найти нельзя.
Слайд 32Полный граф и его свойства
Граф называют нулевым, если в нем есть
вершины, но нет ребер(1)
Если не все вершины соединены ребрами, то граф называется неполным(2)
В полном графе любые две вершины соединены ребром(3)
Если не все вершины соединены ребрами, то граф называется неполным(2)
В полном графе любые две вершины соединены ребром(3)
3
1
А
В
С
Р
А
В
С
Р
А
В
С
Р
Слайд 33Лемма 4
В полном графе с n вершинами число ребер равно n(n-1)/2
В
полном графе с n вершинами из каждой вершины выходит по n -1 ребер.
Значит, сумма степеней вершин равна
n(n-1). Число ребер в 2 раза меньше , то есть n(n-1)/2.
Значит, сумма степеней вершин равна
n(n-1). Число ребер в 2 раза меньше , то есть n(n-1)/2.
Слайд 35Решение
Вершины 17 – ти угольника – вершины графа, диагонали и стороны
– ребра графа. Всего 17*(17 -1)/2=136 ребер. Из них 17 сторон, остальные диагонали. Значит 136 – 17 = 119
Слайд 36Задача 11
Ваня и Миша играют в такую игру. Они по очереди
связывают 5 столбиков ленточками попарно. Кто свяжет последнюю пару столбиков, тот выиграл. Кто победит – тот, кто завяжет первую ленточку, или его соперник?
Слайд 37Решение
После того как все ленты будут завязаны, получится полный граф с
5 вершинами и 5*(5-1)/2=10ребер. Значит выигрывает тот, кто завяжет ленту вторым.
Слайд 38Задача 12
В сарае 10 корыт с едой и 20 поросят.
Через
некоторое время поросята перебегают от одного корыта к другому.
Известно, что от каждого корыта ккаждому перебегал какой – нибудь поросенок. Докажите, что хоть один поросенок перебегал не менее трех раз.
Известно, что от каждого корыта ккаждому перебегал какой – нибудь поросенок. Докажите, что хоть один поросенок перебегал не менее трех раз.
Слайд 39Решение
Обозначим корыта точками- вершинами графа. Если между ними пробегал поросенок, то
вершины графа соединим ребром. Если от каждого корыта к каждому пробегал какой – нибудь поросенок, то граф полный, и в нем проведено хотя бы 10*9/2=45 ребер.
Если бы каждый поросенок перебежал
от одного корыта к другому не более 2 раз, то ребер провели бы не более 20*2 = 40. Значит, хоть один поросенок перебегал не менее трех раз.
Если бы каждый поросенок перебежал
от одного корыта к другому не более 2 раз, то ребер провели бы не более 20*2 = 40. Значит, хоть один поросенок перебегал не менее трех раз.
Слайд 40Путь, маршрут и цикл в графе
Маршрутом в графе называется последовательность ребер,
в которой соседние ребра имеют общую вершину.
Первая вершина называется началом. А последняя - концом.
Первая вершина называется началом. А последняя - концом.
Слайд 41Путем(или цепью) в графе называется маршрут, в котором нет повторяющихся ребер.
Если в пути нет повторяющихся вершин, его называют простым путем. Длина маршрута равна количеству ребер в порядке их прохождения. Расстоянием между вершинами в графе называют длину кратчайшего пути от одной вершины до другой.
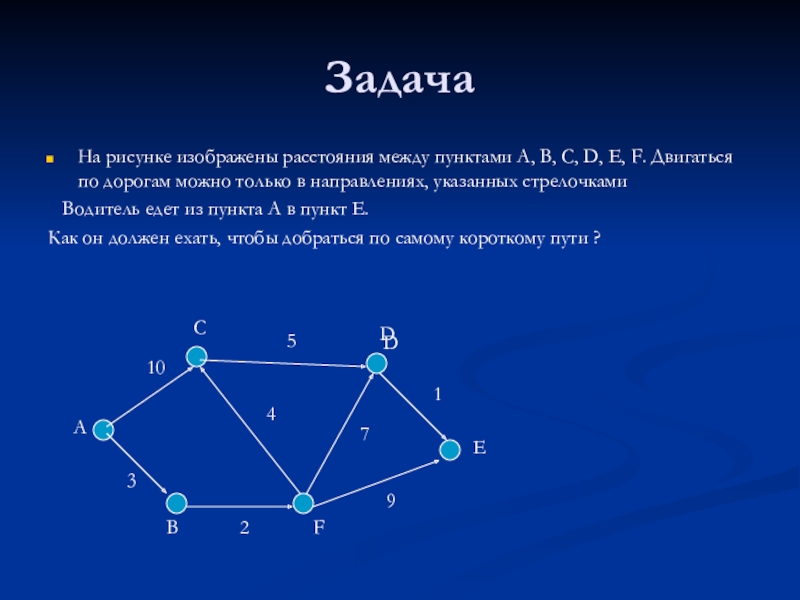
Слайд 42Задача
На рисунке изображены расстояния между пунктами А, В, С, D, Е,
F. Двигаться по дорогам можно только в направлениях, указанных стрелочками
Водитель едет из пункта А в пункт Е.
Как он должен ехать, чтобы добраться по самому короткому пути ?
Водитель едет из пункта А в пункт Е.
Как он должен ехать, чтобы добраться по самому короткому пути ?
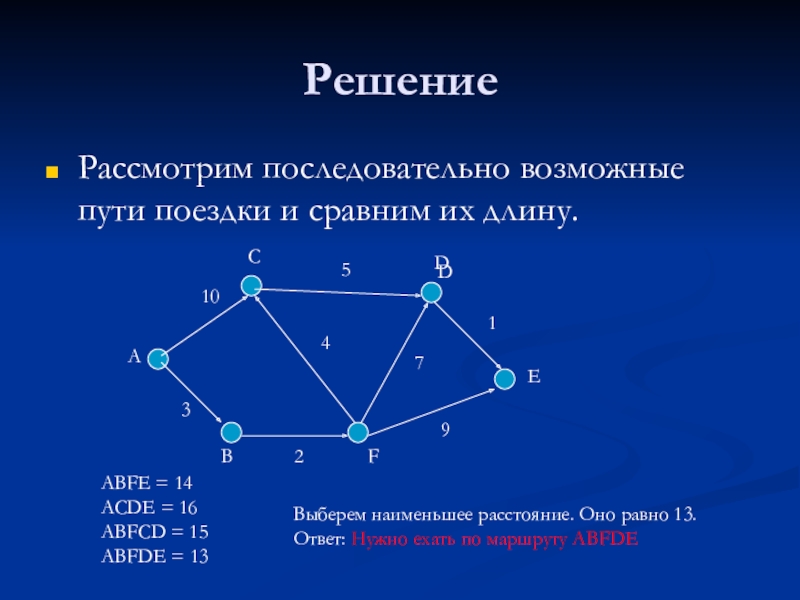
Слайд 43Решение
Рассмотрим последовательно возможные пути поездки и сравним их длину.
ABFE = 14
ACDE
= 16
ABFCD = 15
ABFDE = 13
ABFCD = 15
ABFDE = 13
Выберем наименьшее расстояние. Оно равно 13.
Ответ: Нужно ехать по маршруту ABFDE
