- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Теория вероятностей и математическая статистика на тему Дискретные случайные величины
Содержание
- 1. Презентация по дисциплине Теория вероятностей и математическая статистика на тему Дискретные случайные величины
- 2. 1. Общее понятие случайной величиныСлучайной величиной (СВ)
- 3. 1. Общее понятие случайной величиныРазличают:(!!) Очевидно, что
- 4. 2. Закон и ряд распределения ДСВДля полной
- 5. 2. Закон и ряд распределения ДСВ
- 6. 2. Закон и ряд распределения ДСВ
- 7. Пример 1.В денежной лотерее выпущено 100 билетов.
- 8. Пример 2.В партии из 8 деталей 5
- 9. 2. Закон и ряд распределения ДСВ
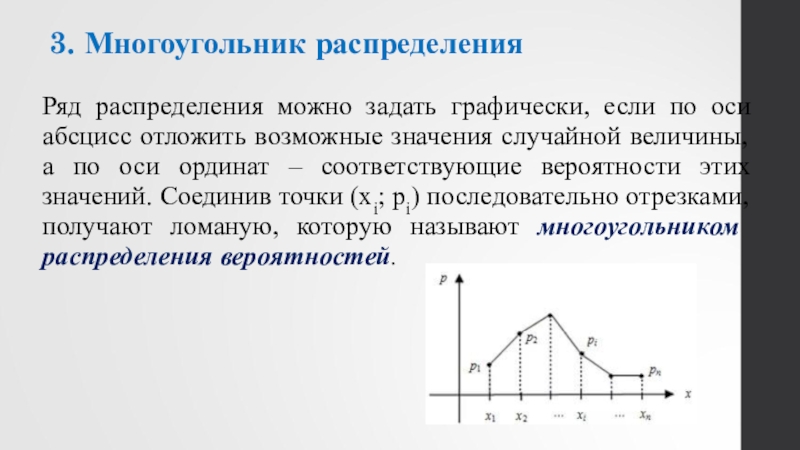
- 10. 3. Многоугольник распределения Ряд распределения можно задать
- 11. 4. Понятие функции распределения СВ
- 12. 4. Понятие функции распределения СВ
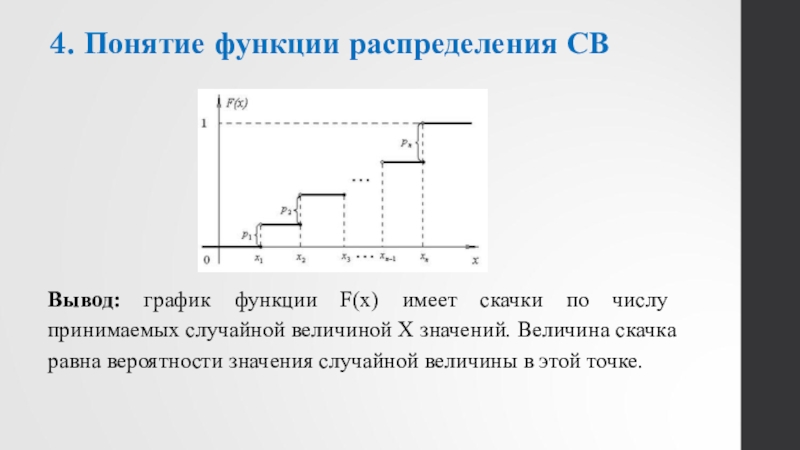
- 13. 4. Понятие функции распределения СВ Вывод: график
- 14. Пример 3.Пусть производятся три выстрела по мишени
- 15. Пример 4.Пусть событие А – «появление одного
Слайд 1Дискретные случайные величины
Беляева Татьяна Юрьевна
ГБПОУ КК «Армавирский машиностроительный техникум»
Преподаватель математических дисциплин
Слайд 21. Общее понятие случайной величины
Случайной величиной (СВ) называется такая переменная величина,
Обозначение:
случайные величины – Х, У, Z, …(возможно с индексами)
значения случайных величин – x, у, z, … (возможно с индексами)
Слайд 31. Общее понятие случайной величины
Различают:
(!!) Очевидно, что значение случайной величины есть
Слайд 42. Закон и ряд распределения ДСВ
Для полной характеристики ДСВ необходимо знать
Вероятность того, что ДСВ Х принимает значение х, обозначают р(Х = х).
Слайд 52. Закон и ряд распределения ДСВ
Соответствие между возможными значениями
Слайд 7Пример 1.
В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в
Х – «сумма выигрыша»
р(Х = 50000) = 1/100 = 0,01
р(Х = 1000) = 10/100 = 0,1
р(Х = 0) = 0,89
Слайд 8Пример 2.
В партии из 8 деталей 5 стандартных. Наудачу взяты 4
Х – «число стандартных деталей среди отобранных»
р(Х = 1) = … = 1/14
р(Х = 2) = … = 6/14
р(Х = 3) = … = 6/14
р(Х = 4) = … = 1/14
Слайд 103. Многоугольник распределения
Ряд распределения можно задать графически, если по оси
Слайд 134. Понятие функции распределения СВ
Вывод: график функции F(x) имеет скачки
Слайд 14Пример 3.
Пусть производятся три выстрела по мишени с вероятностью поражения цели
Х – «число набранных очков»
р(Х = 0) = … = 0,027
р(Х = 5) = … = 0,189
р(Х = 10) = … = 0,441
р(Х = 15) = … = 0,343