- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Использование теоремы Виета при решении рациональных уравнений
Содержание
- 1. Презентация Использование теоремы Виета при решении рациональных уравнений
- 2. … Невозможно избавиться от чувства, что математические
- 3. ЦельРасширить знания и возможности по данной теме
- 4. ЗадачиДоказать теорему Виета для квадратных уравнений, рассмотреть
- 5. Краткая историческая справкаФрансуа Виет(1540—1603) - французский математик.
- 6. Знаменитые «формулы Виета» для коэффициентов многочлена как
- 7. Формулы ВиетаЕсли числа
- 8. Теорема ВиетаСумма корней приведённого квадратного уравнения x2
- 9. Доказательство Пусть дано приведённое квадратное уравнение x2 + bx + c = 0. Если
- 10. Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного
- 11. Теорема, обратная теореме ВиетаЕсли для чисел х1,
- 12. Докажем теорему, обратную теореме Виета. Для удобства
- 13. a>0,c0-2 различных корняa>0,c0-2 различных корняa>0,c>0,D0,c0-2 различных корня a>0,c>0,D>02 различных корняa>0,c>0,D>02 различных корняa>0,c>0,D
- 14. Приведенное квадратное уравнение
- 15. Пусть x1 и x2 – корни приведенного
- 16. Приведенное кубическое уравнение Если x1, x2, x3
- 17. Выполняя аналогичные действия для приведенного кубического уравнения
- 18. Если x1,x2,x3,- корни
- 19. Задача 1Решить уравнение: x3-4x2+x+6=0.1 способ: При а=1
- 20. 2 способ: применение теоремы Виета для решения
- 21. Задача 2
- 22. Задача 3Вычислить, используя теорему Виета, сумму квадратов
- 23. Задача 4Составить кубическое уравнение, корнями которого являются
- 24. Приведенное уравнение четвертой степениЕсли x1, x2, x3,
- 25. Задача 5
- 26. Все математики знали, что под их алгеброй…
- 27. ВыводВ данной работе мною достигнуты поставленные цели:
… Невозможно избавиться от чувства, что математические формулы живут собственной жизнью и обладают собственным разумом, что они умнее нас, умнее даже тех, кто их открыл, что мы получаем из этих формул больше, чем в них было
Слайд 2 … Невозможно избавиться от чувства, что математические формулы живут собственной жизнью
и обладают собственным разумом, что они умнее нас, умнее даже тех, кто их открыл, что мы получаем из этих формул больше, чем в них было изначально заложено.
Генрих Герц
Генрих Герц
Слайд 3Цель
Расширить знания и возможности по данной теме за пределы страниц школьного
учебника, путём обобщения теоремы Виета для уравнений высших степеней и применения специальных методов решения задач.
Слайд 4Задачи
Доказать теорему Виета для квадратных уравнений, рассмотреть её применение на примерах;
Доказать теорему Виета для кубических уравнений и уравнений четвёртой степени;
Убедиться в практичности применения данной теоремы;
Углубить математические знания в области решения уравнений;
Развить интерес к математике.
Слайд 5Краткая историческая справка
Франсуа Виет(1540—1603) - французский математик.
В 1591 году ввёл
буквенные обозначения не только для неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало впервые возможным выражение свойств уравнений и их корней общими формулами.
Ему принадлежит установление единообразного приёма решения уравнений 2-й, 3-й и 4-й степеней.
В тригонометрии Франсуа Виет дал полное решение задачи об определении всех элементов плоского или сферического треугольника по трём данным.
Ему принадлежит установление единообразного приёма решения уравнений 2-й, 3-й и 4-й степеней.
В тригонометрии Франсуа Виет дал полное решение задачи об определении всех элементов плоского или сферического треугольника по трём данным.
Слайд 6Знаменитые «формулы Виета» для коэффициентов многочлена как функций его корней.
Новый тригонометрический
метод решения неприводимого кубического уравнения. Виет применил его для решения древней задачи трисекции угла, которую свёл к кубическому уравнению.
Виет дал первое в Европе аналитическое представление числа π, правильно вычислив 9 десятичных знаков.
Полное аналитическое изложение теории уравнений первых четырёх степеней.
Идея применения трансцендентных функций к решению алгебраических уравнений.
Оригинальный метод приближённого решения алгебраических уравнений.
Частичное решение задачи Аполлония о построении круга, касающегося трёх данных, в сочинении Apollonius Gallus (1600). Решение Виета не подходит для случая внешних касаний
Умер Франсуа Виет в возрасте 63 лет в 1603г.
Виет дал первое в Европе аналитическое представление числа π, правильно вычислив 9 десятичных знаков.
Полное аналитическое изложение теории уравнений первых четырёх степеней.
Идея применения трансцендентных функций к решению алгебраических уравнений.
Оригинальный метод приближённого решения алгебраических уравнений.
Частичное решение задачи Аполлония о построении круга, касающегося трёх данных, в сочинении Apollonius Gallus (1600). Решение Виета не подходит для случая внешних касаний
Умер Франсуа Виет в возрасте 63 лет в 1603г.
Слайд 7Формулы Виета
Если числа
– корни многочлена n-ой степени
то справедливы равенства:
Эти равенства называются формулами Виета. Выпишем их отдельно для многочленов второго, третьего и четвертого порядков.
Эти равенства называются формулами Виета. Выпишем их отдельно для многочленов второго, третьего и четвертого порядков.
Слайд 8Теорема Виета
Сумма корней приведённого квадратного уравнения x2 + px + q
= 0 равна коэффициенту p, взятому с противоположным знаком, а произведение корней равно свободному члену q:
В общем случае (для неприведенного квадратного уравнения):
В общем случае (для неприведенного квадратного уравнения):
Слайд 9Доказательство
Пусть дано приведённое квадратное уравнение x2 + bx + c = 0. Если его дискриминант больше нуля,
то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Докажем, что равенства x1 + x2 = −b и x1 × x2 = c имеют место быть.
Вспомним формулы корней квадратного уравнения:
Найдём сумму корней x1 и x2.
Для этого подставим в выражение x1 + x2 вместо x1 и x2 соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Сократим дробь на 2, тогда получим −b
Значит x1 + x2 действительно равно −b
x1 + x2 = −b
Теперь аналогично докажем, что произведение x1 × x2 равно свободному члену c.
Докажем, что равенства x1 + x2 = −b и x1 × x2 = c имеют место быть.
Вспомним формулы корней квадратного уравнения:
Найдём сумму корней x1 и x2.
Для этого подставим в выражение x1 + x2 вместо x1 и x2 соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Сократим дробь на 2, тогда получим −b
Значит x1 + x2 действительно равно −b
x1 + x2 = −b
Теперь аналогично докажем, что произведение x1 × x2 равно свободному члену c.
Слайд 10Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что
коэффициент a всё ещё равен единице:
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В числителе теперь содержится (a + b)(a − b). Воспользуемся тождеством (a + b)(a − b) = a2 − b2. Тогда в числителе полýчится А знаменатель будет равен 4
Теперь в числителе выражение (−b)2 станет равно b2, а выражение станет равно просто D
Но D равно b2 − 4ac. Подстáвим это выражение вместо D, не забывая что a = 1. То есть вместо b2 − 4ac надо подставить b2 − 4c
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Значит x1 × x2 действительно равно c.
x1 × x2 = c
Таким образом, сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком (x1 + x2 = −b), а произведение корней равно свободному члену (x1 × x2 = c).
Теорема доказана.
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В числителе теперь содержится (a + b)(a − b). Воспользуемся тождеством (a + b)(a − b) = a2 − b2. Тогда в числителе полýчится А знаменатель будет равен 4
Теперь в числителе выражение (−b)2 станет равно b2, а выражение станет равно просто D
Но D равно b2 − 4ac. Подстáвим это выражение вместо D, не забывая что a = 1. То есть вместо b2 − 4ac надо подставить b2 − 4c
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Значит x1 × x2 действительно равно c.
x1 × x2 = c
Таким образом, сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком (x1 + x2 = −b), а произведение корней равно свободному члену (x1 × x2 = c).
Теорема доказана.
Слайд 11Теорема, обратная теореме Виета
Если для чисел х1, х2, p, q справедливы
формулы:
то х1 и х2 – корни уравнения
то х1 и х2 – корни уравнения
х1+х2=-p,
х1·х2=q
х2+px+q=0
Слайд 12Докажем теорему, обратную теореме Виета. Для удобства корни x1 и x2 обозначим как m и n. Тогда утверждение
теоремы, обратной теореме Виета примет следующий вид:
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x2 + bx + c = 0, то числа m иn являются корнями уравнения x2 + bx + c = 0
Для начала запишем, что сумма m и n равна −b, а произведение mn равно c
Чтобы доказать, что числа m и n являются корнями уравнения x2 + bx + c = 0, нужно поочередно подстáвить буквы m и n в это уравнение вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x2 + bx + c = 0.
Помимо букв m и n нам нужно знать чему равен параметр b. Выразим его из равенства m + n = −b. Легче всего это сделать, умножив обе части этого равенства на −1
Теперь всё готово для подстановок. Подстáвим m в уравнение x2 + bx + c = 0 вместо x, а выражение −m − n подставим вместо b
Видим, что при x = m получается верное равенство. Значит число mявляется корнем уравнения x2 + bx + c = 0.
Аналогично докажем, что число n является корнем уравнения x2 + bx + c = 0. Подставим вместо x букву n, а вместо c подставим mn, поскольку c = mn.
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Следовательно, числа m и n являются корнями уравнения x2 + bx + c = 0.
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x2 + bx + c = 0, то числа m иn являются корнями уравнения x2 + bx + c = 0
Для начала запишем, что сумма m и n равна −b, а произведение mn равно c
Чтобы доказать, что числа m и n являются корнями уравнения x2 + bx + c = 0, нужно поочередно подстáвить буквы m и n в это уравнение вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x2 + bx + c = 0.
Помимо букв m и n нам нужно знать чему равен параметр b. Выразим его из равенства m + n = −b. Легче всего это сделать, умножив обе части этого равенства на −1
Теперь всё готово для подстановок. Подстáвим m в уравнение x2 + bx + c = 0 вместо x, а выражение −m − n подставим вместо b
Видим, что при x = m получается верное равенство. Значит число mявляется корнем уравнения x2 + bx + c = 0.
Аналогично докажем, что число n является корнем уравнения x2 + bx + c = 0. Подставим вместо x букву n, а вместо c подставим mn, поскольку c = mn.
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Следовательно, числа m и n являются корнями уравнения x2 + bx + c = 0.
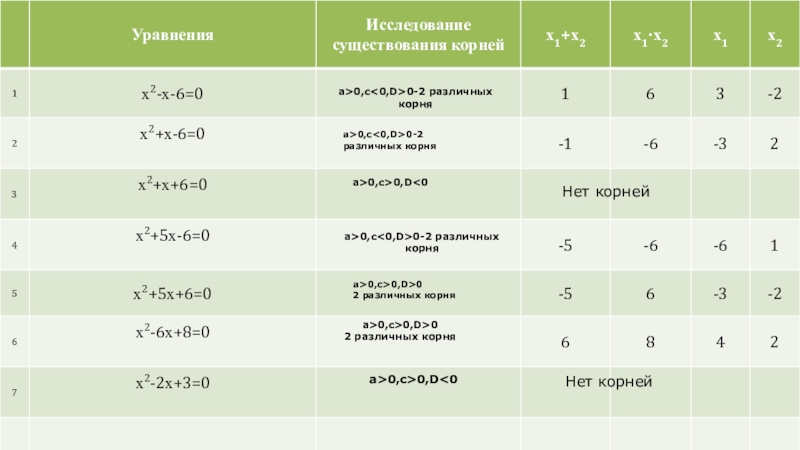
Слайд 13a>0,c0-2 различных корня
a>0,c0-2 различных корня
a>0,c>0,D0,c0-2 различных корня
a>0,c>0,D>0
2 различных
корня
a>0,c>0,D>0
2 различных корня
a>0,c>0,D<0
Нет корней
Слайд 15Пусть x1 и x2 – корни приведенного квадратного уравнения
x2 +
px + q = 0
Перемножим двучлены (х - x1) и (х - x2) :
(х - x1)(х - x2) = x2 - (x1+ x2)х + x1x2 ,
Тогда, сравнивая с исходным уравнением можно записать систему :
Перемножим двучлены (х - x1) и (х - x2) :
(х - x1)(х - x2) = x2 - (x1+ x2)х + x1x2 ,
Тогда, сравнивая с исходным уравнением можно записать систему :
Слайд 16Приведенное кубическое уравнение
Если x1, x2, x3 – корни кубического уравнения
x3 + bx2 + cx + d = 0, то
Слайд 17
Выполняя аналогичные действия для приведенного кубического уравнения x3+ax2+bx+c=0, считая x1,x2,x3 корнями
исходного кубического уравнения, получаем:
(х-x1)(х-x2)(х-x3) = x3 – (x1+x2+x3 ) x2+(x1x2+ x1x3 + x2,x3)х - x1x2x3
следовательно, имеет место следующая система равенств:
следовательно, имеет место следующая система равенств:
Слайд 18 Если x1,x2,x3,- корни неприведённого кубического уравнения
ax3 + bx2 + cx + d = 0, то
x1+x2+x3=- b/a
(х1*х2+х1*х3+х2*х3)= с/а
х1*х2*х3=-d/a
есть суть теоремы Виета для кубического уравнения.
(х1*х2+х1*х3+х2*х3)= с/а
х1*х2*х3=-d/a
есть суть теоремы Виета для кубического уравнения.
Слайд 19Задача 1
Решить уравнение: x3-4x2+x+6=0.
1 способ: При а=1 свободный член этого уравнения
раскладывают на простые множители, затем поочередно выбирают значения «x», равные одному из этих множителей с различными знаками. Эти значения х проверяют, подставляя их в исходное равенство. Таким способом иногда удается найти первый корень кубического уравнения х1. Для нахождения остальных корней надо соответствующий многочлен разделить на выражение (х-х1), при этом в частном получается квадратный трехчлен. Корни получившегося квадратного трехчлена также являются корнями кубического уравнения. Таким образом 6=1*2*3, т.е.корни уравнения могут быть числа 1 или -1,2 или-2,3 или-3. Способом подстановки выясняем, что х1=-1.Разделим многочлен х3-4х2+х+6 на (х+1) и получим трехчлен
х2-5х+6, т.е.х3-4х2+х+6=(х+1)*(х2-5х+6)=0.
Найдем корни квадратного уравнения х2-5х+6=0 по теореме Виета: х1=2 и х2=3.
Таким образом исходное кубическое уравнение имеет три действительных корня:
х1=-1, х2=2, х3=3.
х2-5х+6, т.е.х3-4х2+х+6=(х+1)*(х2-5х+6)=0.
Найдем корни квадратного уравнения х2-5х+6=0 по теореме Виета: х1=2 и х2=3.
Таким образом исходное кубическое уравнение имеет три действительных корня:
х1=-1, х2=2, х3=3.
Слайд 202 способ: применение теоремы Виета для решения кубического уравнения
Итак, если х3-4х2+х+6=0,
то х1+х2+х3=4
Х1*х2+х1*х3+х2*х3=1,
Х1*х2*х3=-6
Методом подбора находим: (-1)*2*3=-6
(-1)+2+3=4
(-1)*2+(-1)*3+2*3=1,
т.е корни уравнения
х1=-1,х2=2, х3=3.
Слайд 22Задача 3
Вычислить, используя теорему Виета, сумму квадратов корней уравнения х3-6х2+11х-6=0
Согласно
теореме Виета имеем:
х1+х2+х3=6
х1*х2*х3=6
х1*х2+х1*х3+х2*х3=11
Т.к. (х1+х2+х3)2=х12+х22+х32+2(х1*х2+х1*х3+х2*х3), то получим 62=х12+х22+х32+2*11
36-22= х12+х22+х32
х12+х22+х32=14 Ответ: 14
х1+х2+х3=6
х1*х2*х3=6
х1*х2+х1*х3+х2*х3=11
Т.к. (х1+х2+х3)2=х12+х22+х32+2(х1*х2+х1*х3+х2*х3), то получим 62=х12+х22+х32+2*11
36-22= х12+х22+х32
х12+х22+х32=14 Ответ: 14
Слайд 23Задача 4
Составить кубическое уравнение, корнями которого являются числа -5;3;4
Решение:
Пусть х1=-5,
х2=3,х3=4, тогда
А теперь составим приведенное кубическое уравнение вида x3+ax2+bx+c=0, корнями которого являются -5, 3, 4.
Это будет уравнение x3-2x2-23x+60=0
А теперь составим приведенное кубическое уравнение вида x3+ax2+bx+c=0, корнями которого являются -5, 3, 4.
Это будет уравнение x3-2x2-23x+60=0
Слайд 24Приведенное уравнение четвертой степени
Если x1, x2, x3, x4 – корни уравнения
четвертой степени
x4 + bx3 + cx2 + dx + e = 0, то
x4 + bx3 + cx2 + dx + e = 0, то
Слайд 26Все математики знали, что под их алгеброй… были скрыты несравненные сокровища,
но не умели их найти; задачи, которые они считали наиболее трудными, совершенно легко решаются десятками с помощью нашего искусства, представляющего поэтому самый верный путь для математических изысканий.
Слайд 27Вывод
В данной работе мною достигнуты поставленные цели: я узнал о научной
деятельности Ф. Виета, его вкладе в математику, ознакомился с формулами для решения приведенных уравнений третьей и четвертой степени, закрепил новые знания, с помощью решения задач.
Умение использовать теорему Виета, во многом облегчает решение математических и физических задач в курсе средней школы. Особенно этот навык незаменим при подготовке к ЕГЭ.
Таким образом, теорема Виета помогает быстро находить корни квадратного уравнения, она применима к решению уравнений высших степеней. В ряде случаев при решении уравнений высших степеней удобнее применять Теорему Виета и с ее помощью решение будет рациональнее.
Это исследование было для меня очень познавательным. Углубив свои знания в математике, я открыл для себя много полезного и интересного.
Умение использовать теорему Виета, во многом облегчает решение математических и физических задач в курсе средней школы. Особенно этот навык незаменим при подготовке к ЕГЭ.
Таким образом, теорема Виета помогает быстро находить корни квадратного уравнения, она применима к решению уравнений высших степеней. В ряде случаев при решении уравнений высших степеней удобнее применять Теорему Виета и с ее помощью решение будет рациональнее.
Это исследование было для меня очень познавательным. Углубив свои знания в математике, я открыл для себя много полезного и интересного.