Алматы 2015
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад и конспект урока по статистике на тему Мода и медиана в статистике. Открытый урок.Определите расход ткани на одно изделие в среднем по фабрике.
Содержание
- 1. Презентация и конспект урока по статистике на тему Мода и медиана в статистике. Открытый урок.Определите расход ткани на одно изделие в среднем по фабрике.
- 2. «Статистика знает всё», - утверждали Ильф и
- 3. 1. Средние в статистике
- 4. 3. Найти средние :д.е.РешениеОпределите среднюю годовую процентную
- 5. Задача 2. На основе приведенных данных вычислить среднюю цену хлеба.д.е.Решение
- 6. Задача 3. По семи цехам швейной фабрики
- 7. Когда нужно и не нужно среднее арифметическое?
- 8. Модой называют число ряда, которое встречается в этом
- 9. Когда нужна мода?(варианты ответов студентов)Мода применяется в тех
- 10. Нахождение моды далеко не всегда позволяет делать
- 11. Когда нужна и не нужна медиана?(варианты ответов
- 12. Исчисление моды и медианы в дискретном и интервальном рядах
- 13. Модой называется значение признака (варианта), чаще всего встречающееся в изучаемой совокупности.
- 14. В дискретном ряду распределения модой является вариант
- 15. Для интервального ряда распределения мода определяется по
- 16. Пример: Распределение рабочих по стажу работы характеризуется следующими данными.Определить моду интервального ряда распределения.
- 17. Решение:В данном примере модальный интервал находится в
- 18. Медиана – это значение признака у единицы
- 19. Для нахождения медианы в дискретном ряду строится
- 20. Для нахождения медианы в интервальном ряду используют
- 21. Пример: Распределение рабочих по стажу работы характеризуется следующими данными.
- 22. Определим медианный интервал. Им считается тот, до
- 23. Обобщение изученного материалаДалеко не
- 24. Пример 1. На спартакиаде колледжа проводится несколько
- 25. Пример 2. Перед нами ранжированный ряд, представляющий данные
- 26. Немного юмора (высказывания о статистике):Статистика - наука,
- 27. По данным таблиц определить моду и медиану.Самостоятельная
- 28. Домашнее задание Задача 1. Возводимая площадь на
- 29. В заключение нашего урока ответьте, пожалуйста, на
- 30. Используемые сайтыhttp://fb.ru/article/108141/mediana-v-statistike-ponyatie-svoystva-i-raschethttp://fb.ru/article/108141/mediana-v-statistike-ponyatie-svoystva-i-raschet#image239723http://ramki-vsem.ru/kliparty-zhivotnye.htmlhttp://www.neurosoft.ru/rus/product/book/hrv-2/chapter5.aspx(http://nirvana.tomsk.ru/dictionary?id=9&word=%EC%E5%E4%E8%E0%ED%E0/)
- 31. Спасибо за внимание!Успехов в приобретении знаний!
Слайд 1Открытый урок по статистике
Структурные средние:
мода, медиана
Разработала преподаватель специальных дисциплин
Зотова
Слайд 2«Статистика знает всё», - утверждали Ильф и Петров в своем знаменитом
«Известно, сколько какой пищи съедает в год средний гражданин республики...
Известно, сколько в стране охотников, балерин... станков, велосипедов, памятников, маяков и швейных машинок...
Как много жизни, полной
пыла, страстей и мысли,
глядит на нас
со статистических таблиц!..»
Слайд 43. Найти средние
:
д.е.
Решение
Определите среднюю годовую процентную ставку.
Задача 1. В течение
=(11+7+8+8+11+11+12+9+10)/9=87/9=9,7%
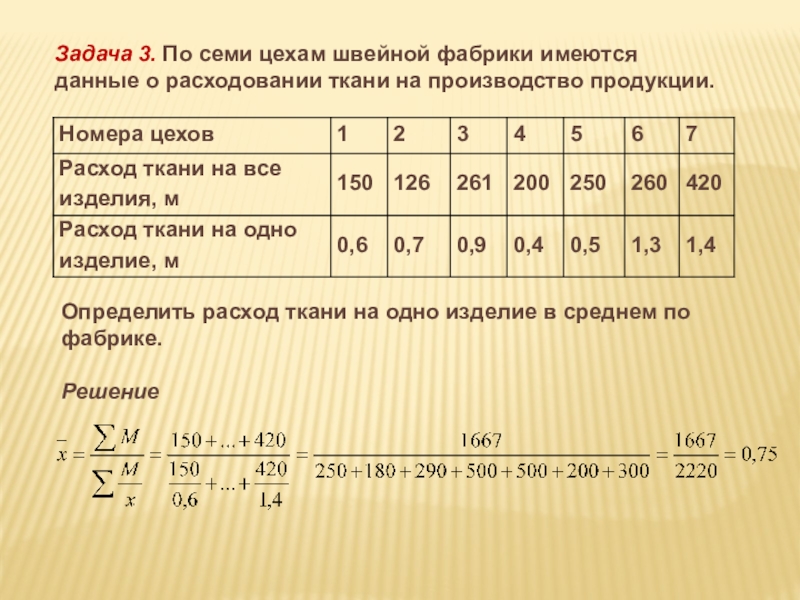
Слайд 6Задача 3. По семи цехам швейной фабрики имеются
данные о расходовании
м
Определить расход ткани на одно изделие в среднем по фабрике.
Решение
Слайд 7Когда нужно и не нужно
среднее арифметическое?
(варианты ответов студентов):
Сравнение уровня
Вычисление средних трат в семье на продукты, средней урожайности картофеля на огороде, средних расходов на продукты, чтобы понять, как поступать в следующий раз, чтобы не было большого перерасхода, средней оценки за семестр – по ней поставят оценку за год.
НО !
Нет смысла вычислять среднюю зарплату моей мамы и главы администрации президента, среднюю температуру здорового и больного человека, средний размер обуви у меня и у моего брата.
Слайд 8Модой называют число ряда, которое встречается в этом ряду наиболее часто. Можно
Такой показатель, как мода, используется не только для числовых данных. Если, например, опросить большую группу студентов, какая из дисциплин им нравится больше всего, то модой этого ряда ответов окажется та дисциплина, которую будут называть чаще остальных.
Оценки за семестр по статистике: 4,5,5,4,4,4,4,5,5,4,5,5,4,5,5,5,5,5,5.
Получилось: «5» - 7, «4» - 5, «3» - 0, «2» - 0
Мода равна 5.
Но мода бывает не одна, например, по статистике в октябре у студентки были такие оценки – 4,4,5,4,4,3,5,5,5.
Мод здесь две – 4 и 5
Мода – показатель, широко используемый в статистике.
Одним из наиболее частых использований моды является изучение спроса. Например, при решении вопросов, в пачки какого веса фасовать масло, какие открывать авиарейсы и т. п., предварительно изучается спрос и выявляется мода – наиболее часто встречающийся заказ.
.
Слайд 9Когда нужна мода?
(варианты ответов
студентов)
Мода применяется в тех случаях, когда нужно охарактеризовать
Если надо, например, узнать наиболее распространенный размер заработной платы на предприятии, цену на рынке, по которой было продано наибольшее количество товаров,
самый популярный фасон и размер одежды, обуви, размер бутылки сока, пачки чипсов, пользующийся наибольшим спросом у потребителей, и т.д., в этих случаях прибегают к моде.
Слайд 10Нахождение моды далеко не всегда позволяет делать надежные выводы на основе
Еще одной из важных статистических характеристик ряда данных является его медиана. Обычно медиану ищут в случае, когда числа в ряду являются какими-либо показателями и надо найти, например, человека, показавшего средний результат, фирму со средней годовой прибылью, авиакомпанию, предлагающую средние цены на билеты, и т. д.
При анализе результатов, показанных участниками забега на 100 метров, знание медианы позволяет преподавателю физкультуры выделить для участия
в соревнованиях группу ребят, показавших результат выше срединного.
Слайд 11Когда нужна и не нужна медиана?
(варианты ответов студентов)
Медиана чаще применяется с
выше или ниже медианы.
Пример: в одной и той же больничной палате находится девять человек с температурой 36,6 °С, и один человек, у которого она равна 41 °С. Арифметическое среднее в этом случае равно: (36,6*9+41)/10 = 37,04 °С. Но это вовсе не означает, что каждый из присутствующих болен. Все это наталкивает на мысль, что одной средней часто бывает недостаточно, и именно поэтому в дополнение к ней используется медиана.
На выполнение домашнего задания студент тратит в течение недели такое время – 60 мин в понедельник, во вторник 103 мин, в среду 58, в четверг 76, а в пятницу 89 мин.
Записав эти числа от меньшего к большему, увидим, что посередине стоит число 76 – это называется медиана.
Слайд 13Модой
называется значение признака (варианта),
чаще всего встречающееся
в изучаемой совокупности.
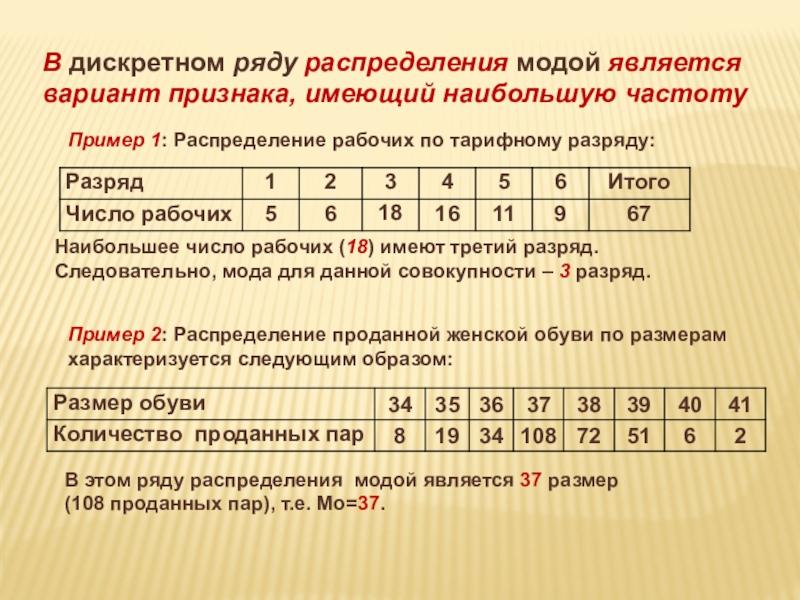
Слайд 14В дискретном ряду распределения модой является вариант признака, имеющий наибольшую частоту
Пример
Наибольшее число рабочих (18) имеют третий разряд.
Следовательно, мода для данной совокупности – 3 разряд.
Пример 2: Распределение проданной женской обуви по размерам характеризуется следующим образом:
В этом ряду распределения модой является 37 размер
(108 проданных пар), т.е. Мо=37.
Слайд 15Для интервального ряда распределения мода определяется по формуле:
где
ХMo - нижняя граница
hMo - величина модального интервала;
fMo – частота модального интервала;
fMo-1 и fMo+1 – частота интервала соответственно предшествующего модальному
и следующего за ним
Слайд 16Пример: Распределение рабочих по стажу работы характеризуется следующими данными.
Определить моду интервального
Слайд 17Решение:
В данном примере модальный интервал
находится в пределах стажа работы
6-8
Мода интервального ряда составляет
Слайд 18Медиана –
это значение признака у единицы совокупности, делящая ранжированный ряд
(или стоящая
в середине
ранжированного
ряда).
Слайд 19Для нахождения медианы в дискретном ряду строится ряд накопленных частот.
Рабочих с
т. е. превышает порядковый номер медианы.
Отсюда следует, что рабочий, имеющий порядковый номер 34, принадлежит к 4-й тарифной группе.
Следовательно, медиана в нашем примере - 4 разряд.
В данной совокупности, состоящей из 68 единиц, в середине ранжированного ряда будет находиться 34-й рабочий
Слайд 20Для нахождения медианы в интервальном ряду
используют формулу:
где Ме
Х0 - нижняя граница медианного интервала (накопленная частота которого содержит единицу, стоящую в середине ряда);
hMe - величина медианного интервала
Σf - сумма частот ряда (численность совокупностей);
SMe-1 - накопленная частота предмедианного интервала предшествующего медианному);
fMe - частота медианного интервала.
Слайд 22Определим медианный интервал.
Им считается тот, до которого сумма накопленных частот
4, 27, 47, 82, 93,100.
Середина накопленных частот - 100/2 = 50.
Сумма первых трех меньше половины (47 < 50),
а если прибавить 35 - больше половины численности совокупности (82 > 50).
Следовательно, медианным является интервал 6-8.
Определим медиану:
Слайд 23
Обобщение изученного материала
Далеко не всегда имеет смысл вычислять
Слайд 24
Пример 1. На спартакиаде колледжа проводится несколько квалификационных забегов на 100
15,5; 16,8; 21,8; 18,4; 16,2; 32,3; 19,9; 15,5; 14,7; 19,8; 20,5; 15,4.
Проранжируем ряд:
14,7; 15,4; 15,5; 15,5; 16,2; 16,8; 18,4; 19,8; 19,9; 20,5; 21,8; 32,3.
Найдем все три характеристики.
Какая характеристика, по-вашему, самая подходящая?
Мо=15,5
Для ответа на вопрос нужно определить медиану
Слайд 25Пример 2. Перед нами ранжированный ряд, представляющий
данные о времени дорожно-транспортных происшествий
0:15, 0:55, 1:20, 3:20, 4:10, 6:30, 7:15, 7:45, 8:40, 9:05, 9:20,
9:40, 10:15, 11:30, 12:10, 12:15, 13:10, 13:50, 14:10, 14:20, 14:25,
15:20, 15:45, 16:20, 16:25, 17:05, 17:30, 17:45, 17:55, 18:05, 18:15,
18:45, 18:50, 19:45, 19:55, 20:30, 20:40, 21:30, 21:45, 22:10, 22:35.
Как и для любого ряда, в данном случае мы можем найти среднее
арифметическое – оно равно 13:33.
Однако вряд ли имеет какой-то смысл утверждение типа «аварии на улицах города происходят в среднем в 13 часов 33 минуты».
В то же время, если сгруппировать данные этого ряда в интервалы,
можно найти такой временной интервал, когда происходит наибольшее количество ДТП (такую характеристику называют интервальной модой).
Получив такую характеристику, соответствующие службы должны
серьезно проанализировать, почему именно в этот временной интервал происходит наибольшее количество происшествий, и попытаться устранить их причины.
Слайд 26Немного юмора
(высказывания о статистике):
Статистика - наука, занимающаяся изготовлением
недостоверных фактов
(Эван Эсари)
Статистика может доказать что угодно, даже правду
(Ноэл Мойнихан)
Статистика - это наука о том, сколько всего приходится на каждого человека, если бы все делились справедливо. (Константин Мелихан)
Статистики как судебные психиатры –
они могут подтвердить правоту обеих сторон
(Фиорелло Да Тардиа)
Не принимай на веру того, что говорит статистика,
пока тщательно не изучишь, о чем она умалчивает
(Уильям Уотт)
Статистика, пожалуй, это самая божественная из наук. Ведь она переводит любое событие из разряда случайного
в разряд закономерного.
Для политиков статистика - меч, для бюрократов - щит.
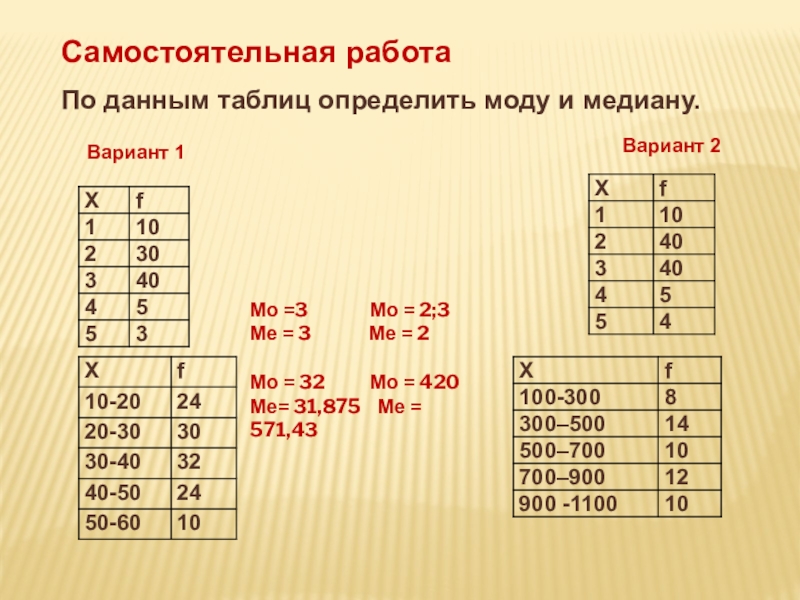
Слайд 27По данным таблиц определить моду и медиану.
Самостоятельная работа
Вариант 1
Вариант 2
Мо =3
Ме = 3 Ме = 2
Мо = 32 Мо = 420
Ме= 31,875 Ме = 571,43
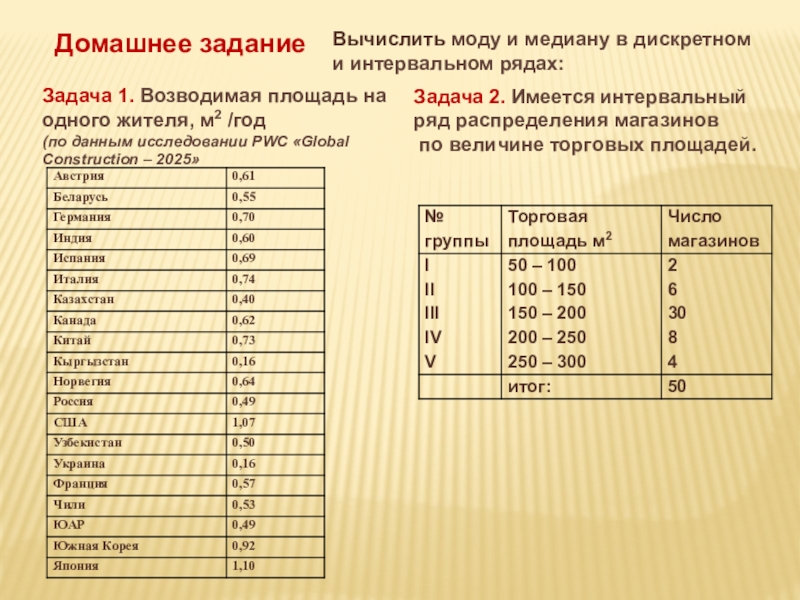
Слайд 28Домашнее задание
Задача 1. Возводимая площадь на одного жителя, м2 /год
(по данным исследовании PWC «Global Construction – 2025»
Задача 2. Имеется интервальный ряд распределения магазинов
по величине торговых площадей.
Вычислить моду и медиану в дискретном и интервальном рядах:
Слайд 29В заключение нашего урока ответьте,
пожалуйста, на следующие вопросы:
Что тебе больше
Что тебе меньше всего понравилось? _____________
Я узнал(а) _____________________________________
Еще я хотел(а) бы узнать ________________________
Подведение итогов