Геометрическое тело есть абстракция, в которой сохраняются лишь форма и размеры в полном отвлечении от всех других свойств
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Плоскость, поверхность, геометрическое тело
Содержание
- 1. Плоскость, поверхность, геометрическое тело
- 2. Цели занятия:Образовательные:Формирование у студентов способностей к
- 3. Геометрическим телом называют часть пространства, ограниченной геометрическими поверхностями.Все геометрические тела можно разделить на две группы:МногогранникиТела вращения
- 4. МНОГОГРАННИКИМногогранники-тела, ограниченные со всех сторон плоскостями.Многогранники различают в зависимости от формы и количества граней.
- 5. ПРИЗМАПризма - многогранник, у которого боковые грани
- 6. Прямая четырехугольная призма (параллелепипед)Верхнее основаниеНижнее основаниеРебра основанияБоковые
- 7. Пирамида-многогранник, у которого боковые грани представляют собой
- 8. Прямая правильная шестиугольная пирамидаБоковыеребраВершинаБоковая граньОснованиеРебра основанияВысота
- 9. Тела вращения – тела, ограниченные поверхностью вращенияТела вращения
- 10. Основания цилиндра – круги. Цилиндрическая поверхность образуется
- 11. Прямой круговой конус – тело вращения, ограниченное
- 12. Построение проекций прямого кругового конуса
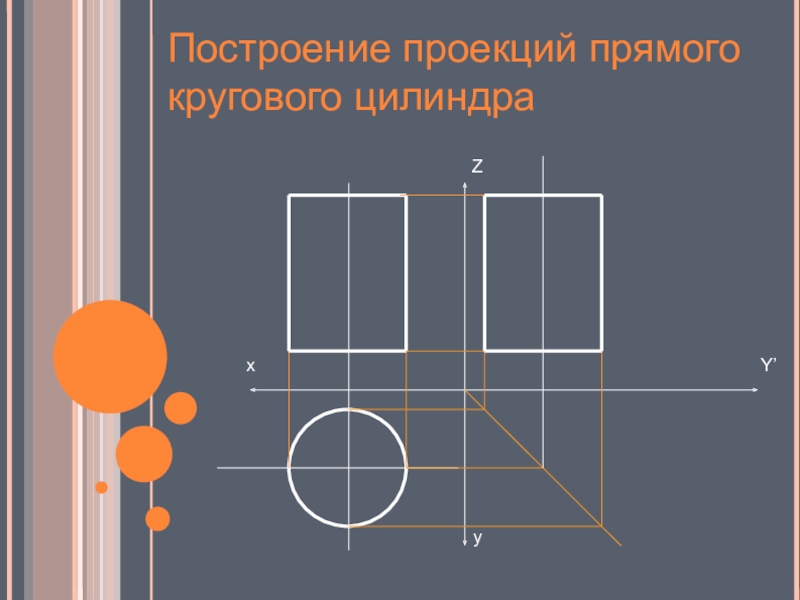
- 13. Построение проекций прямого кругового цилиндра
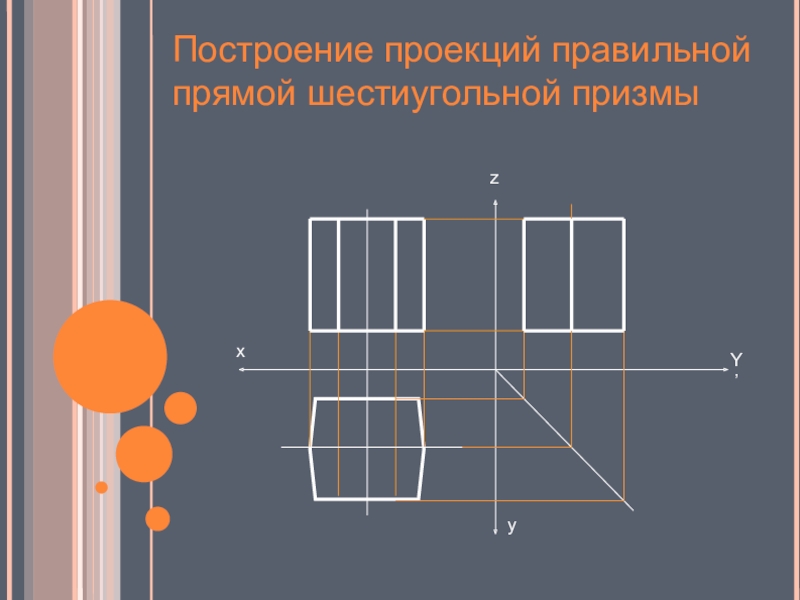
- 14. Построение проекций правильной прямой шестиугольной призмы
- 15. Построение проекций прямой правильной шестиугольной пирамиды
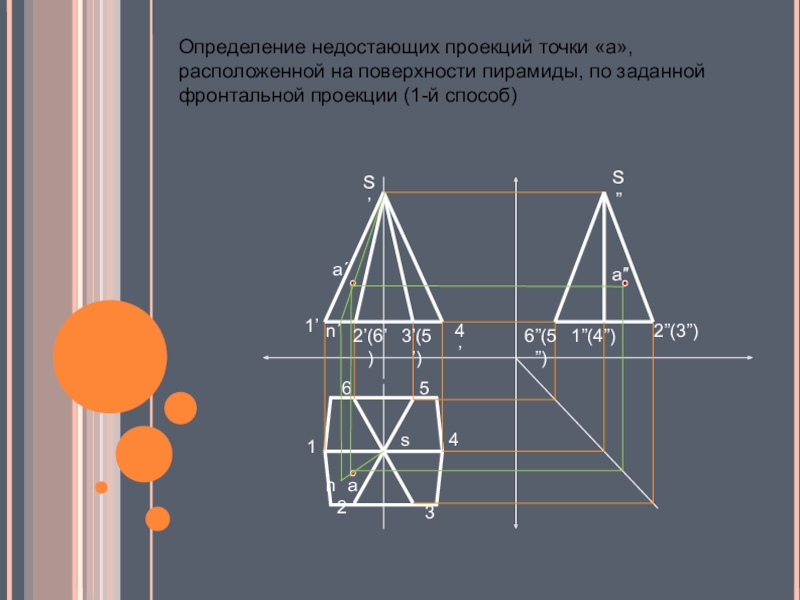
- 16. Определение недостающих проекций точки «а», расположенной на поверхности пирамиды, по заданной фронтальной проекции (1-й способ)
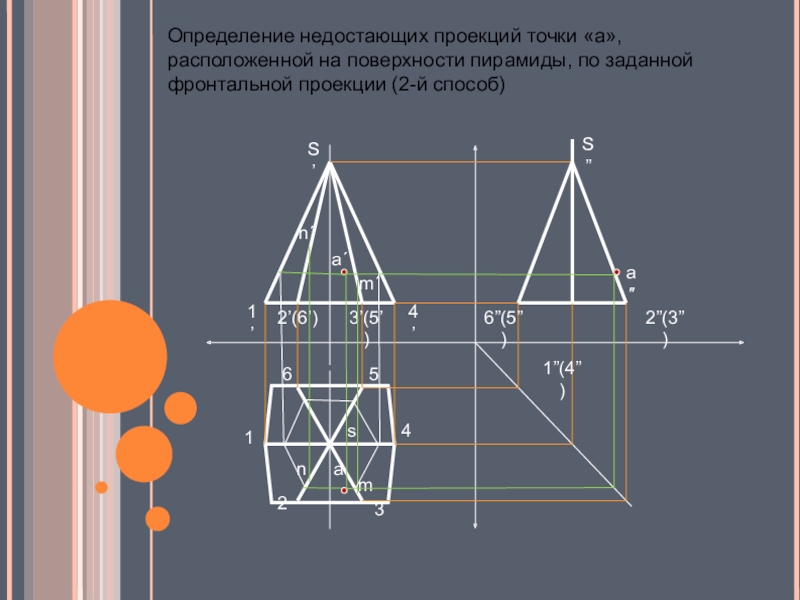
- 17. Определение недостающих проекций точки «а», расположенной на поверхности пирамиды, по заданной фронтальной проекции (2-й способ)
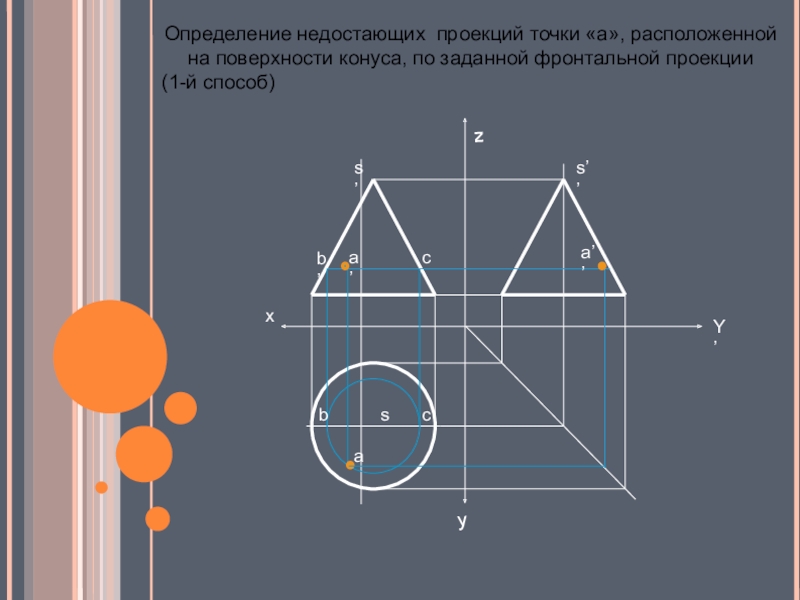
- 18. Определение недостающих проекций точки «а», расположенной на поверхности конуса, по заданной фронтальной проекции (1-й способ)
- 19. Нахождение недостающих проекций точки «а», расположенной на поверхности конуса, по заданной фронтальной проекции (2-й способ)
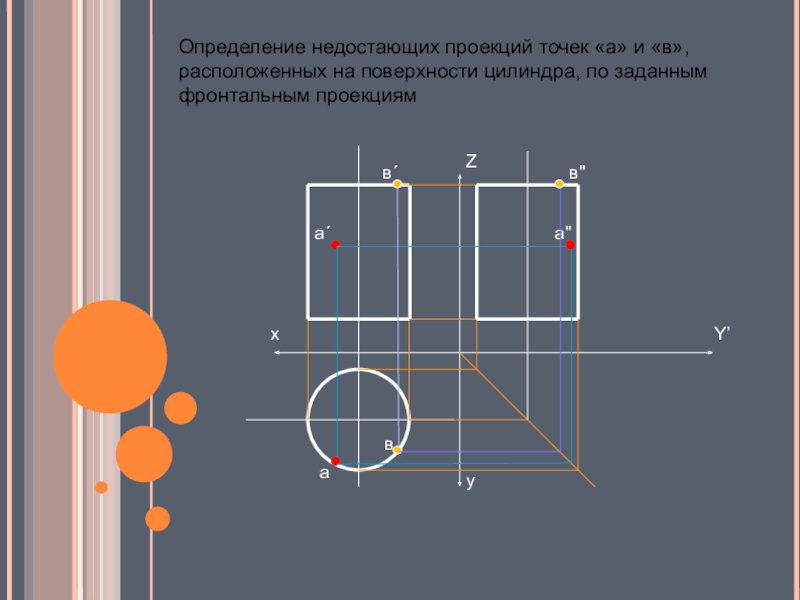
- 20. Определение недостающих проекций точек «а» и «в», расположенных на поверхности цилиндра, по заданным фронтальным проекциям
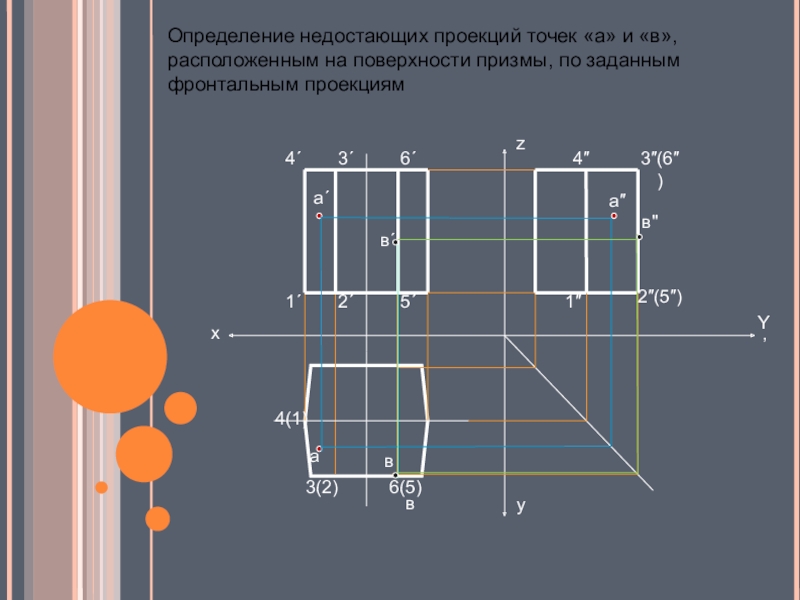
- 21. Определение недостающих проекций точек «а» и «в», расположенным на поверхности призмы, по заданным фронтальным проекциям
- 22. Боголюбов С. К. Инженерная графика – М.:
Цели занятия:Образовательные:Формирование у студентов способностей к самостоятельному и инициативному решению практических задач Закрепление навыков построения в ортогональной системе проецирования, закрепление навыков чтения ортогональных чертежей.Выполнение практической работы по нахождению проекций точек и линий принадлежащих гранным телам,
Слайд 1ТЕМА:
Поверхности и тела.
Нахождение проекций точек и линий принадлежащих гранным телам,
телам вращения.
Слайд 2 Цели занятия:
Образовательные:
Формирование у студентов способностей к самостоятельному и инициативному решению
практических задач
Закрепление навыков построения в ортогональной системе проецирования, закрепление навыков чтения ортогональных чертежей.
Выполнение практической работы по нахождению проекций точек и линий принадлежащих гранным телам, телам вращения.
Развивающие:
Формирование навыков выступления перед аудиторией;
Развитие пространственного воображения;
Развитие навыков работы с ассоциативными образами соответствующими теме задания
Развитие умения самостоятельно мыслить.
Воспитательные:
Воспитание любви к избранной профессии;
Формирование ответственности при выполнении задания, организованности, точности;
Формирование корректного отношения к мнению окружающих.
Закрепление навыков построения в ортогональной системе проецирования, закрепление навыков чтения ортогональных чертежей.
Выполнение практической работы по нахождению проекций точек и линий принадлежащих гранным телам, телам вращения.
Развивающие:
Формирование навыков выступления перед аудиторией;
Развитие пространственного воображения;
Развитие навыков работы с ассоциативными образами соответствующими теме задания
Развитие умения самостоятельно мыслить.
Воспитательные:
Воспитание любви к избранной профессии;
Формирование ответственности при выполнении задания, организованности, точности;
Формирование корректного отношения к мнению окружающих.
Слайд 3Геометрическим телом называют часть пространства, ограниченной геометрическими поверхностями.
Все геометрические тела можно
разделить на две группы:
Многогранники
Тела вращения
Многогранники
Тела вращения
Слайд 4МНОГОГРАННИКИ
Многогранники-тела, ограниченные со всех сторон плоскостями.
Многогранники различают в зависимости от формы
и количества граней.
Слайд 5ПРИЗМА
Призма - многогранник, у которого боковые грани – прямоугольники или параллелограммы,
а основаниями служат два равных многоугольника.
Если у призмы основания - правильные многоугольники, а высота перпендикулярна основанию, то призма – правильная и прямая.
В зависимости от количества сторон основания призмы бывают треугольные, четырехугольные и т. д.
Если у призмы основания - правильные многоугольники, а высота перпендикулярна основанию, то призма – правильная и прямая.
В зависимости от количества сторон основания призмы бывают треугольные, четырехугольные и т. д.
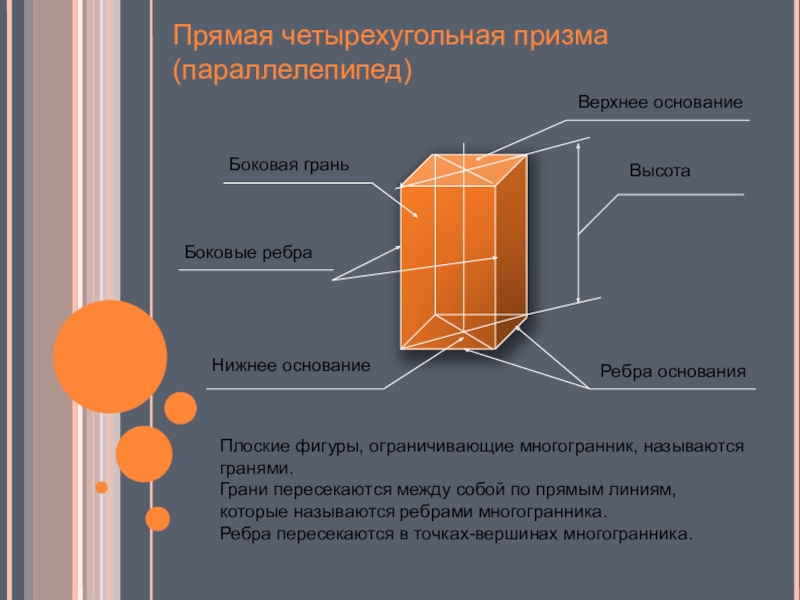
Слайд 6Прямая четырехугольная призма (параллелепипед)
Верхнее основание
Нижнее основание
Ребра основания
Боковые ребра
Высота
Боковая грань
Плоские фигуры, ограничивающие
многогранник, называются гранями.
Грани пересекаются между собой по прямым линиям, которые называются ребрами многогранника.
Ребра пересекаются в точках-вершинах многогранника.
Грани пересекаются между собой по прямым линиям, которые называются ребрами многогранника.
Ребра пересекаются в точках-вершинах многогранника.
Слайд 7Пирамида-многогранник, у которого боковые грани представляют собой треугольники, имеющие общую вершину.
В
основании у пирамиды – многоугольник. В зависимости от количества сторон основания пирамида называется трех-, четырех-, пятиугольной и т. д.
Если у пирамиды основание правильный многоугольник, а высота перпендикулярна основанию, то пирамида правильная и прямая
Если у пирамиды основание правильный многоугольник, а высота перпендикулярна основанию, то пирамида правильная и прямая
Пирамида
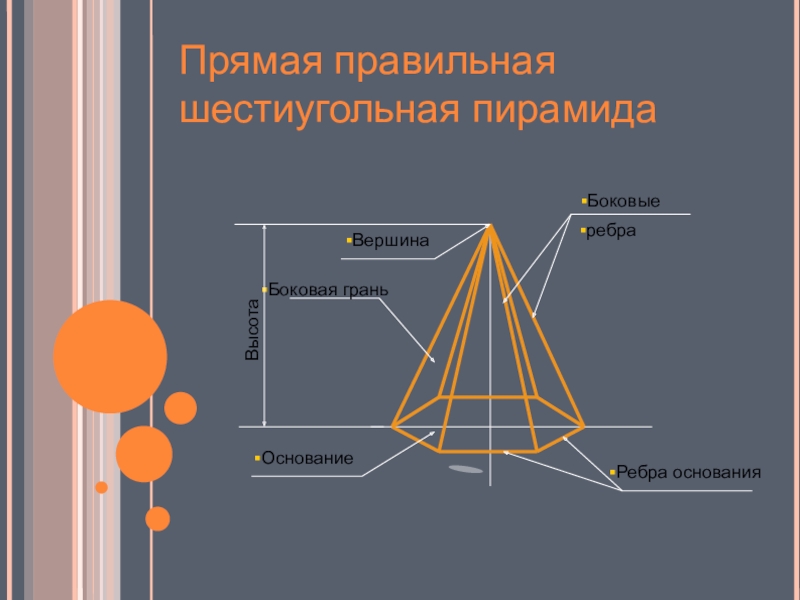
Слайд 8Прямая правильная шестиугольная пирамида
Боковые
ребра
Вершина
Боковая грань
Основание
Ребра основания
Высота
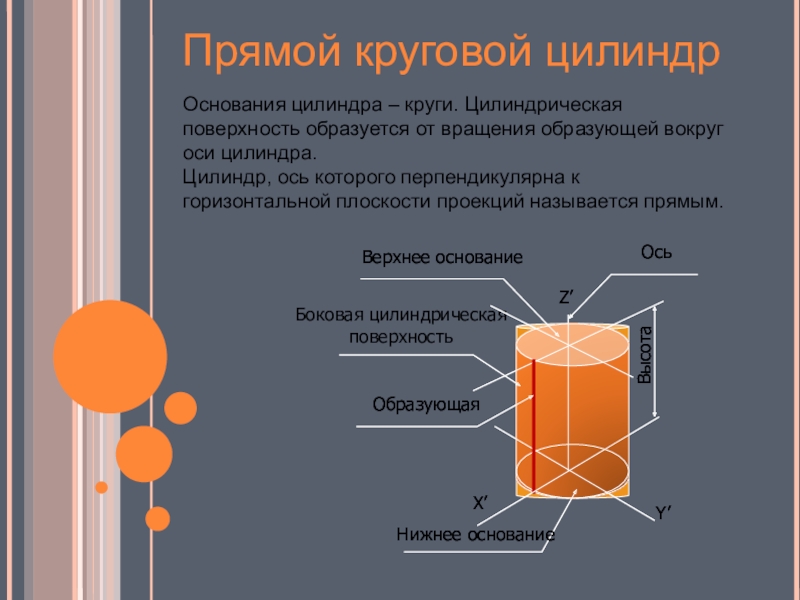
Слайд 10Основания цилиндра – круги. Цилиндрическая поверхность образуется от вращения образующей вокруг
оси цилиндра.
Цилиндр, ось которого перпендикулярна к горизонтальной плоскости проекций называется прямым.
Цилиндр, ось которого перпендикулярна к горизонтальной плоскости проекций называется прямым.
Прямой круговой цилиндр
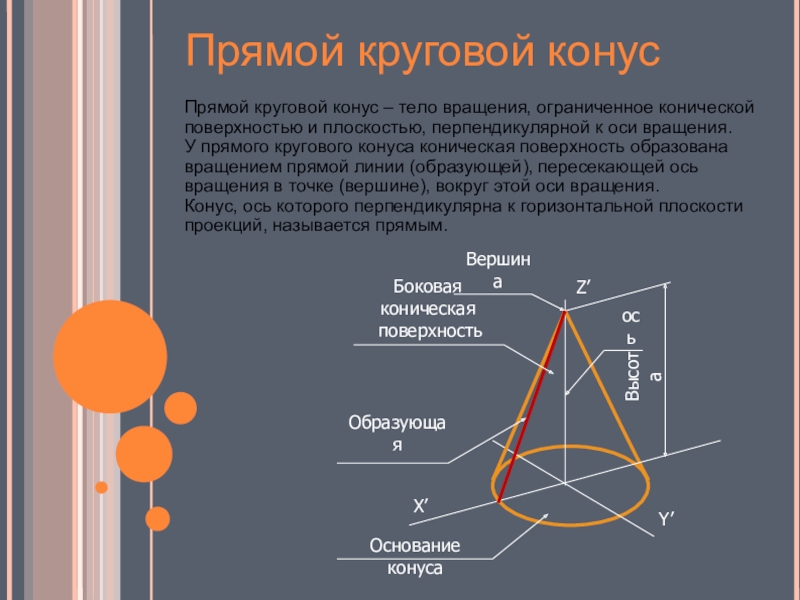
Слайд 11Прямой круговой конус – тело вращения, ограниченное конической поверхностью и плоскостью,
перпендикулярной к оси вращения.
У прямого кругового конуса коническая поверхность образована вращением прямой линии (образующей), пересекающей ось вращения в точке (вершине), вокруг этой оси вращения.
Конус, ось которого перпендикулярна к горизонтальной плоскости проекций, называется прямым.
У прямого кругового конуса коническая поверхность образована вращением прямой линии (образующей), пересекающей ось вращения в точке (вершине), вокруг этой оси вращения.
Конус, ось которого перпендикулярна к горизонтальной плоскости проекций, называется прямым.
Прямой круговой конус
X’
Y’
Z’
Вершина
Высота
ось
Боковая коническая
поверхность
Образующая
Основание конуса
Слайд 16Определение недостающих проекций точки «а», расположенной на поверхности пирамиды, по заданной
фронтальной проекции (1-й способ)
Слайд 17Определение недостающих проекций точки «а», расположенной на поверхности пирамиды, по заданной
фронтальной проекции (2-й способ)
Слайд 18Определение недостающих проекций точки «а», расположенной на поверхности конуса, по заданной
фронтальной проекции
(1-й способ)
(1-й способ)
Слайд 19
Нахождение недостающих проекций точки «а», расположенной на поверхности конуса, по заданной
фронтальной проекции
(2-й способ)
Слайд 20Определение недостающих проекций точек «а» и «в», расположенных на поверхности цилиндра,
по заданным фронтальным проекциям
Слайд 21Определение недостающих проекций точек «а» и «в», расположенным на поверхности призмы,
по заданным фронтальным проекциям
Слайд 22
Боголюбов С. К. Инженерная графика – М.: Машиностроение, 2010.
Куликов В.П. Стандарты
инженерной графики. – М.: И Д «Форум», 2011.
Миронов Р. С. Практические задания по курсу черчения. – М.: Высшая школа, 2010.
Миронов Р. С. Практические задания по курсу черчения. – М.: Высшая школа, 2010.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК