- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение правильных многоугольников и разверток правильных многогранников
Содержание
- 1. Построение правильных многоугольников и разверток правильных многогранников
- 2. Сформировать навыки деления окружности на равные
- 3. Превращение колеса из сплошного
- 4. Иоганн Кеплер(1571- 1630)«Новогодний подарок, или о шестиугольных снежинках»
- 5. Орнаменты и узорыАльбрехт Дюрер(1471-1528).
- 6. Строительство Римский архитектор Ветрувий считал, что при
- 7. «Правильные многоугольники в природе»
- 8. АрхитектураСобор Парижской БогоматериВитраж « Роза»
- 9. Автомобильные дискиЭмблемы и логотипы
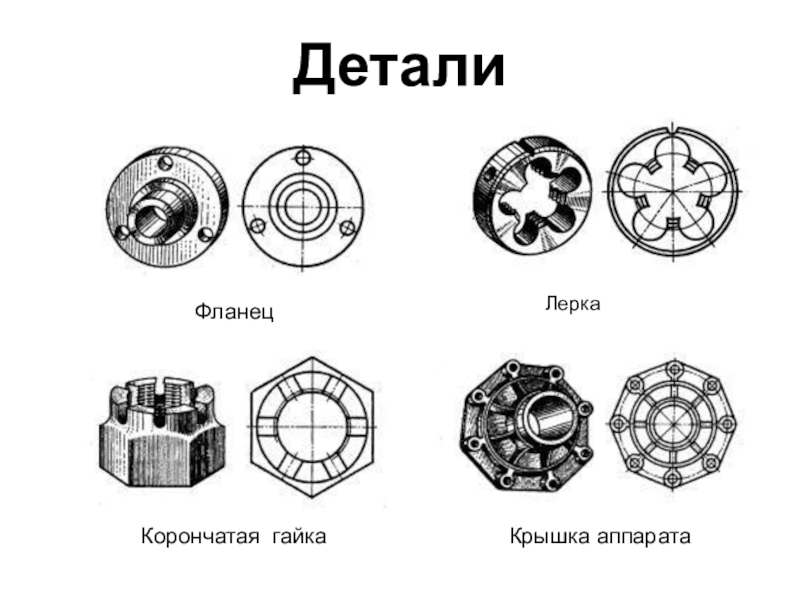
- 10. ДеталиФланецЛеркаКорончатая гайкаКрышка аппарата
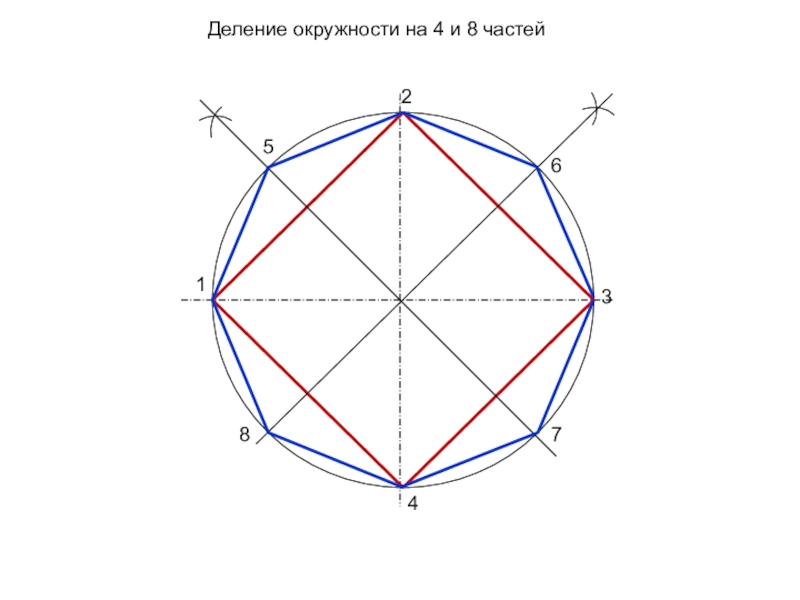
- 11. Деление окружности на 4 и 8 частей12345678
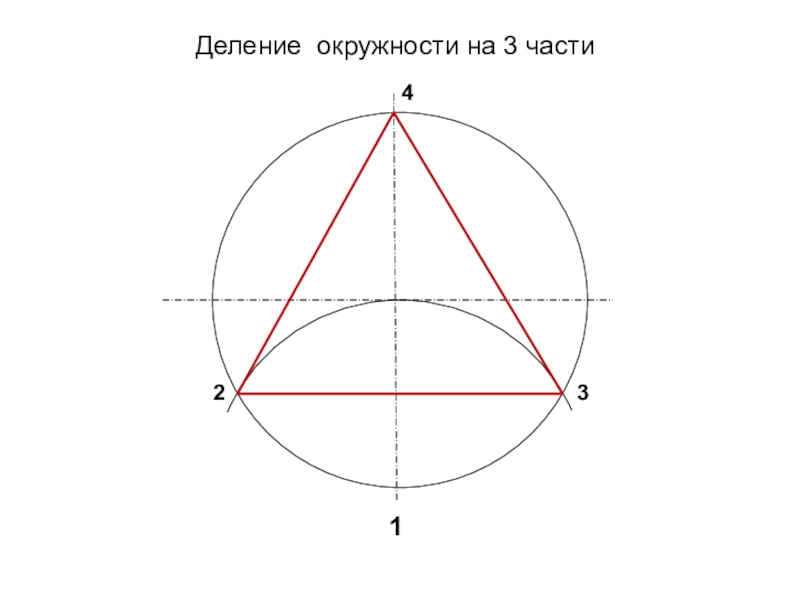
- 12. Деление окружности на 3 части1234
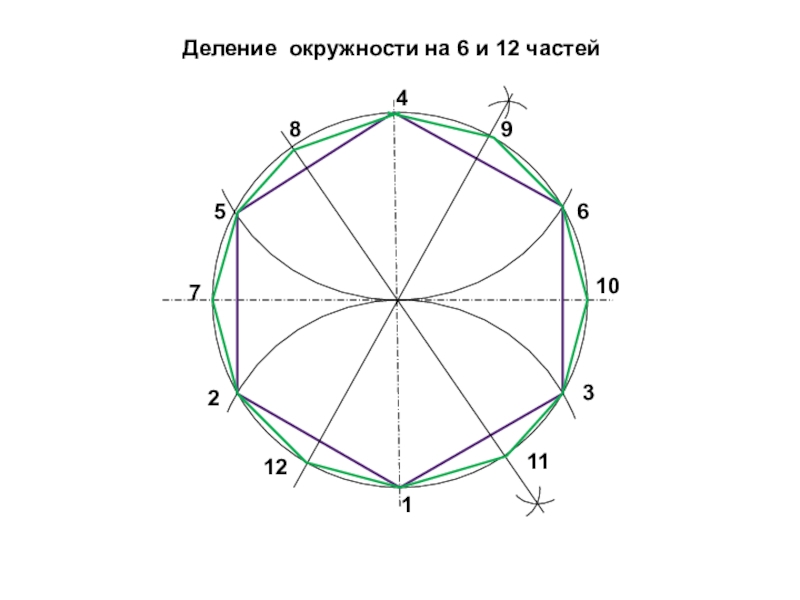
- 13. Деление окружности на 6 и 12 частей132456789101112
- 14. Около любого правильного многоугольника можно описать окружность
- 15. Задание . Какие геометрические построение нужно использовать при построении следующих деталей?
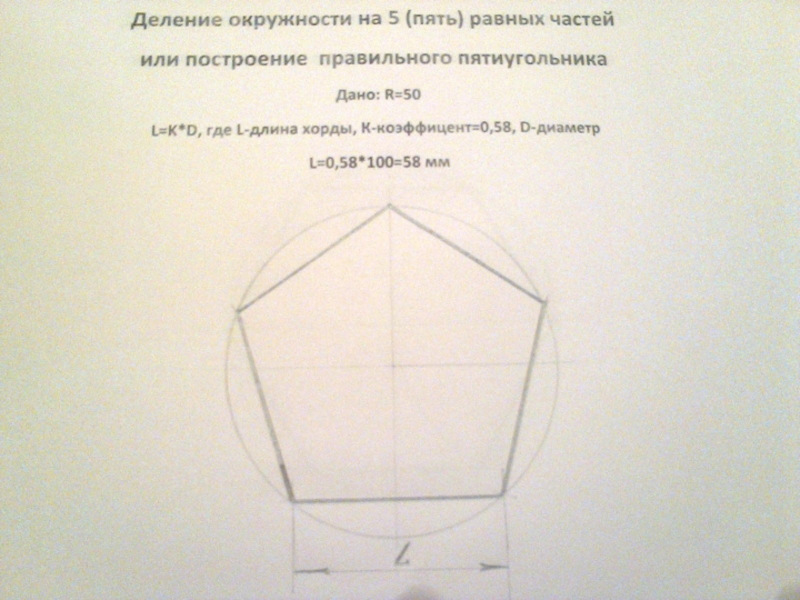
- 16. Построение правильных многоугольников, то есть деление окружности
- 17. Платоновы телаПлатоновы тела - трехмерный аналог плоских
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
Сформировать навыки деления окружности на равные частиФормирование интегрированного подхода при решении задач (комплексное использование знаний, приобретенных на уроках информатики и черчения).Показать необходимость применения геометрических построений при выполнении чертежей детали в программе PAINT и на формате
Слайд 1Тема урока:
Построение правильных многоугольников и разверток правильных многогранников
В знанье — величие
и краса,
Знанье дороже, чем клад жемчужин:
Время любой уничтожит клад,
Мудрый и знающий вечно нужен.
Ас-Самарканди
Слайд 2
Сформировать навыки деления окружности на равные части
Формирование интегрированного подхода при решении
задач (комплексное использование знаний, приобретенных на уроках информатики и черчения).
Показать необходимость применения геометрических построений при выполнении чертежей детали в программе PAINT и на формате А4.
Цели и задачи:
Развивать наблюдательность, умение мыслить логически, умение работать в программе PAINT и на формате А4.
Воспитывать внимательность, аккуратность.
Слайд 3
Превращение колеса из сплошного диска в обод с
о спицами поставило человека перед необходимостью распределить спицы в колесе равномерно. Выполняя изображение такого колеса, люди искали точные способы с помощью чертежных инструментов.
Исторические сведения
Слайд 6Строительство
Римский архитектор Ветрувий считал, что при планировки городов улицы спланировать
нужно так, чтобы вдоль них не дули основные ветра.
Слайд 14Около любого правильного многоугольника можно описать окружность и притом только одну.
Центр – точка пересечения биссектрис.
·
О
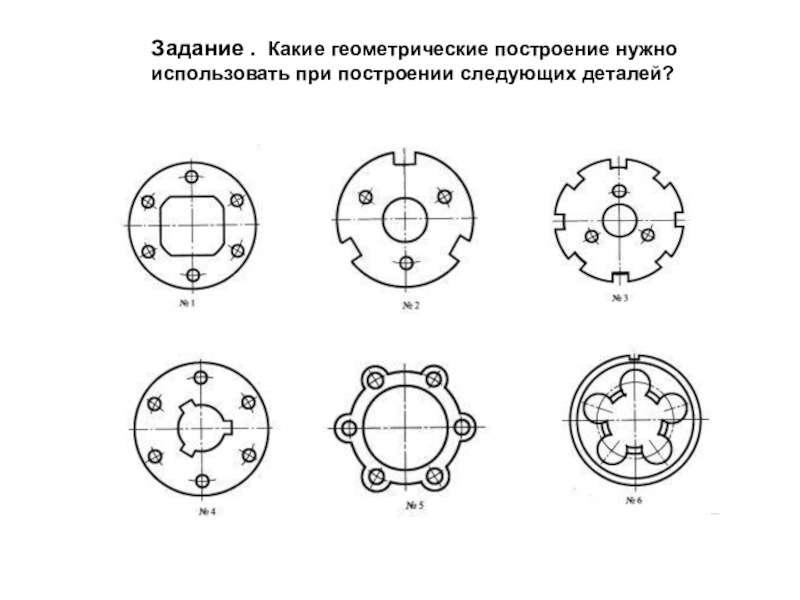
Слайд 15Задание . Какие геометрические построение нужно использовать при построении следующих деталей?
Слайд 16Построение правильных многоугольников, то есть деление окружности на равные части, позволяло
решать практические задачи:
1)Создание колеса со спицами;
2)Деление циферблата часов;
3)Строительство античных театров;
4)Создание астрономических сооружений
1)Создание колеса со спицами;
2)Деление циферблата часов;
3)Строительство античных театров;
4)Создание астрономических сооружений
Слайд 17Платоновы тела
Платоновы тела - трехмерный аналог плоских правильных многоугольников.
Существует лишь пять
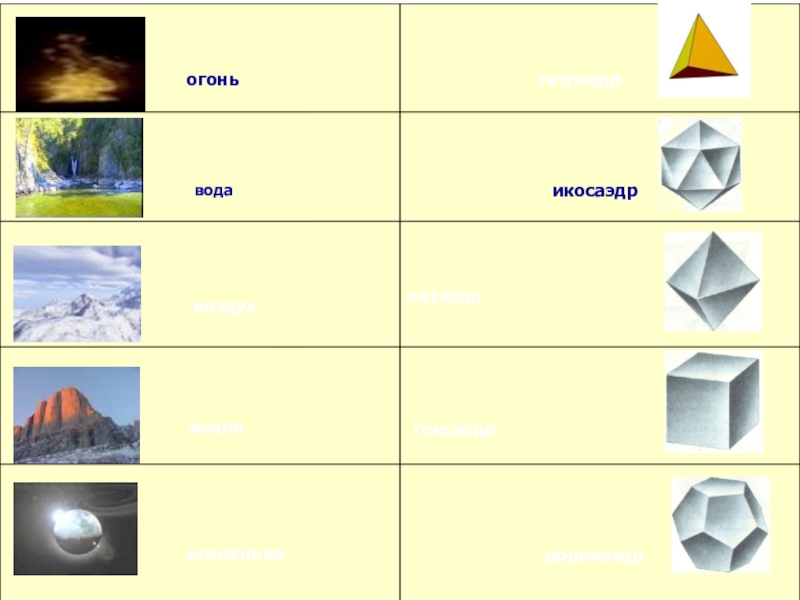
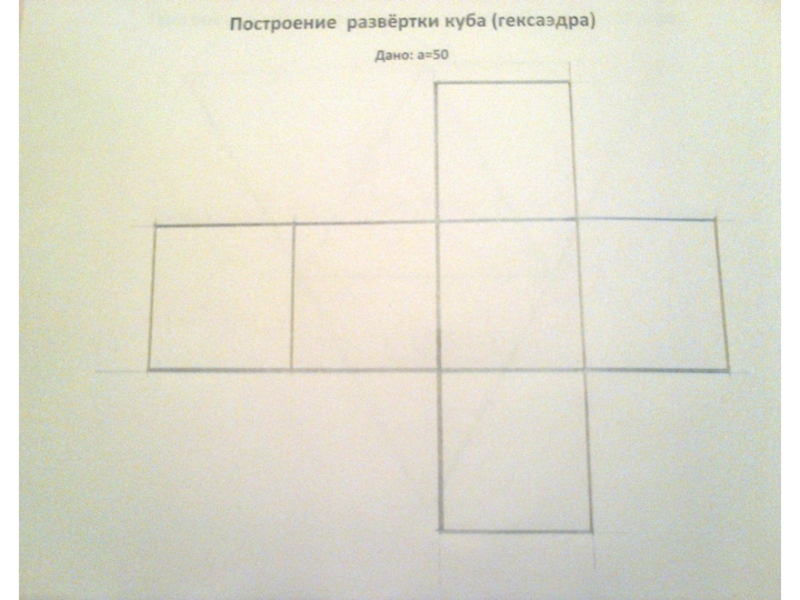
выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.
Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды
.Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.
Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды
.Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.