- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°
Содержание
- 1. Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°
- 2. ПовторениеСинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.Косинусом
- 3. Рассмотрим прямоугольный
- 4. Вспомним основное
- 5. Нахождение значения синуса, косинуса и тангенса для
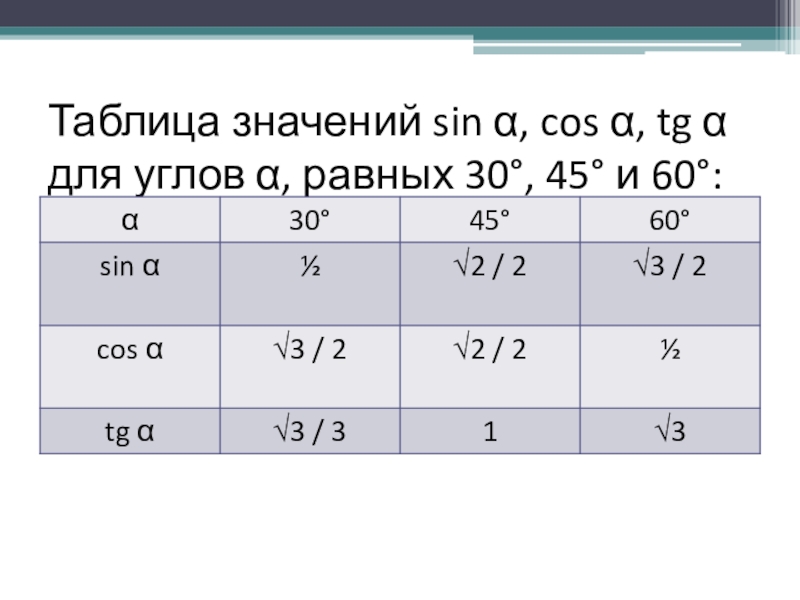
- 6. Таблица значений sin α, cos α, tg α для углов α, равных 30°, 45° и 60°:
- 7. Задачи1. Найдите синус, косинус и тангенс углов
- 8. Решение задачи 1Решение:1. По теореме Пифагора c2
- 9. 3. sin B
- 10. Решение задачи 2Решение:1.Проведём высоты BH и CN.
- 11. 3.Рассмотрим треугольник AHB.Можем выразить
ПовторениеСинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Слайд 2Повторение
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Слайд 3
Рассмотрим прямоугольный треугольник ABC.
∠A=30°,∠B=60°, ∠C=90°.
Так как катет, лежащий против ∠ в 30°, равен половине гипотенузы, то BC/AB = ½.
Но BC/AB = sin A= sin 30°
Также BC/AB = cos B = cos 60°
sin 30° = ½ , cos 60° = ½.
Но BC/AB = sin A= sin 30°
Также BC/AB = cos B = cos 60°
sin 30° = ½ , cos 60° = ½.
Нахождение значения синуса, косинуса и тангенса для углов 30° и 60°
A
B
C
Слайд 4
Вспомним основное тригонометрическое тождество:
sin²α + cos²α
= 1
Из него получим:
cos 30°= √(1- sin²30°)= √(1-1/4) =√3/2,
sin 60° = √(1- cos²60°)= √(1-1/4) =√3/2.
По формуле tg α = sin α / cos α найдём
tg 30° = sin 30° / cos 30° = ½ / (√3/2) = 1/√3 = √3/3,
tg 60° = sin 60° / cos 60° = (√3/2) / ½ = √3.
Из него получим:
cos 30°= √(1- sin²30°)= √(1-1/4) =√3/2,
sin 60° = √(1- cos²60°)= √(1-1/4) =√3/2.
По формуле tg α = sin α / cos α найдём
tg 30° = sin 30° / cos 30° = ½ / (√3/2) = 1/√3 = √3/3,
tg 60° = sin 60° / cos 60° = (√3/2) / ½ = √3.
Слайд 5Нахождение значения синуса, косинуса и тангенса для угла 45°
Рассмотрим прямоугольный треугольник
ABC.
∠A=45°,∠B=45°, ∠C=90°. AC=BC, ∠A=∠B.
По теореме Пифагора AB² = AC² + BC² = 2AC² = 2BC²,
откуда AC = BC = AB / √2
(AB² = 2AC² AC² = AB² / 2 AC = AB / √2 ).
sin 45° = sin A = BC / AB = 1 / √2 = √2 / 2
cos 45° = cos A = AC / AB = 1 / √2 = √2 / 2
tg 45° = tg A = sin A / cos A = 1.
∠A=45°,∠B=45°, ∠C=90°. AC=BC, ∠A=∠B.
По теореме Пифагора AB² = AC² + BC² = 2AC² = 2BC²,
откуда AC = BC = AB / √2
(AB² = 2AC² AC² = AB² / 2 AC = AB / √2 ).
sin 45° = sin A = BC / AB = 1 / √2 = √2 / 2
cos 45° = cos A = AC / AB = 1 / √2 = √2 / 2
tg 45° = tg A = sin A / cos A = 1.
B
A
C
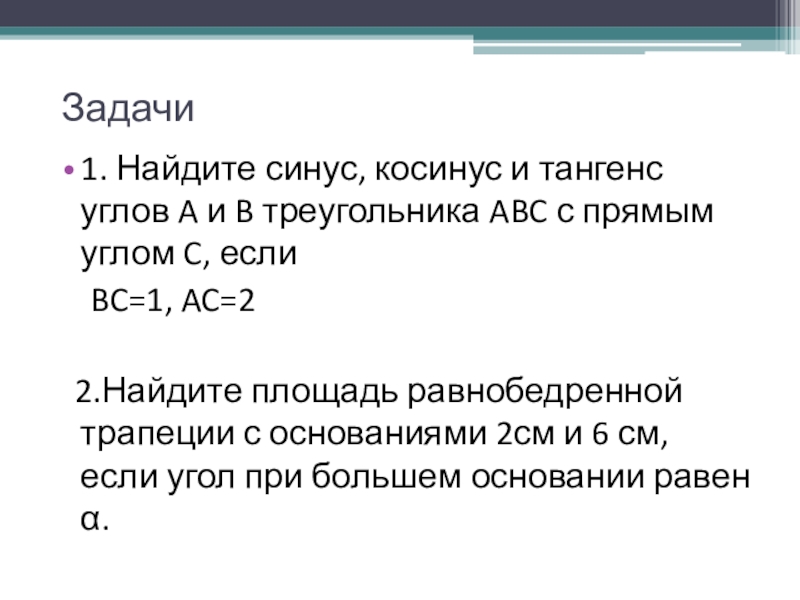
Слайд 7Задачи
1. Найдите синус, косинус и тангенс углов A и B треугольника
ABC с прямым углом C, если
BC=1, AC=2
2.Найдите площадь равнобедренной трапеции с основаниями 2см и 6 см, если угол при большем основании равен α.
BC=1, AC=2
2.Найдите площадь равнобедренной трапеции с основаниями 2см и 6 см, если угол при большем основании равен α.
Слайд 8Решение задачи 1
Решение:
1. По теореме Пифагора c2 = a2 + b2
c2
= 1+4 = 5 с = √5
2. sin A = BC/AB = 1/√5 = √5/5
cos A = AC/AB = 2/√5 = 2√5/5
tg A = sin A/cos A =(√5/5) / (2√5/5) = ½
2. sin A = BC/AB = 1/√5 = √5/5
cos A = AC/AB = 2/√5 = 2√5/5
tg A = sin A/cos A =(√5/5) / (2√5/5) = ½
Дано:
ABC-треугольник
∠C=90°
BC=1, AC=2
Найти sin A, cos A, tg A,
sin B, cos B, tg B
A
B
С
c
a
b
Слайд 9
3. sin B = AC/AB = 2/√5
= 2√5/5
cos B = BC/AB =1/√5 = √5/5
tg B = sin B/cos B = (2√5/5) / (√5/5) = 2
Ответ: sin A = √5/5, cos A = 2√5/5, tg A = ½ ;
sin = 2√5/5, cos B = √5/5, tg B = 2.
cos B = BC/AB =1/√5 = √5/5
tg B = sin B/cos B = (2√5/5) / (√5/5) = 2
Ответ: sin A = √5/5, cos A = 2√5/5, tg A = ½ ;
sin = 2√5/5, cos B = √5/5, tg B = 2.
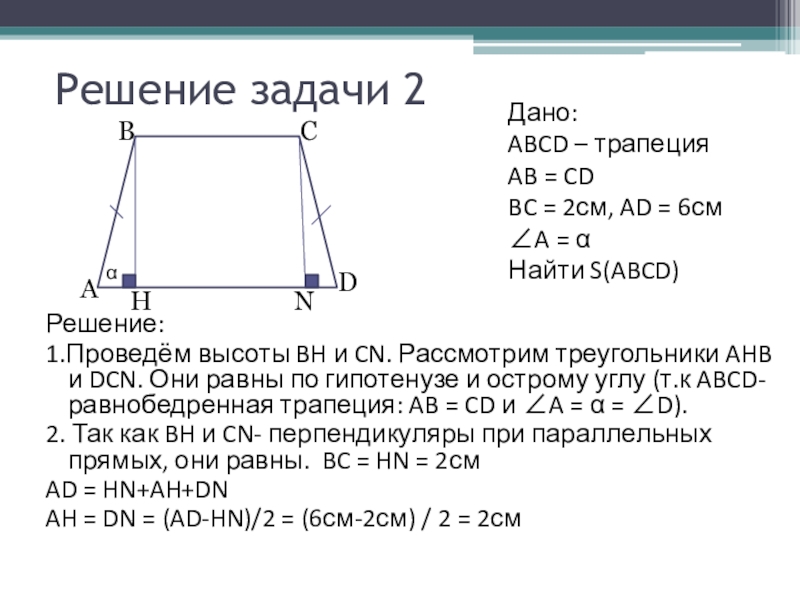
Слайд 10Решение задачи 2
Решение:
1.Проведём высоты BH и CN. Рассмотрим треугольники AHB и
DCN. Они равны по гипотенузе и острому углу (т.к ABCD- равнобедренная трапеция: AB = CD и ∠A = α = ∠D).
2. Так как BH и CN- перпендикуляры при параллельных прямых, они равны. BC = HN = 2см
AD = HN+AH+DN
AH = DN = (AD-HN)/2 = (6см-2см) / 2 = 2см
2. Так как BH и CN- перпендикуляры при параллельных прямых, они равны. BC = HN = 2см
AD = HN+AH+DN
AH = DN = (AD-HN)/2 = (6см-2см) / 2 = 2см
Дано:
ABCD – трапеция
AB = CD
BC = 2см, AD = 6см
∠A = α
Найти S(ABCD)
A
B
C
D
α
H
N
Слайд 11
3.Рассмотрим треугольник AHB.
Можем выразить BH через tg α.
tg α = BH/AH ------ BH = tg α * AH = 2tg α
4. S(ABCD) = ½ (BC+AD) * h = ½ (2+6) * 2tg α =
= 8tg α см 2
Ответ: S(ABCD) = 8tg α см 2.
4. S(ABCD) = ½ (BC+AD) * h = ½ (2+6) * 2tg α =
= 8tg α см 2
Ответ: S(ABCD) = 8tg α см 2.