СОШ №24 пос. Бира
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Выступление на августовской конференции
Содержание
- 1. Выступление на августовской конференции
- 2. «Все наши замыслы, все поиски и построения
- 3. Мотивация – это процесс побуждения себя и других к деятельности для достижения личных целей.
- 4. Приемы и методы, повышающие мотивацию учащихся:Создание проблемной
- 5. Уроки « Одной задачи»Решение развивающих, нестандартных задачДифференцированные
- 6. 1 метод. Использование логических задач в начале урока.
- 7. Куда едет автобус?
- 8. Какое число скрыто под парковочным местом?
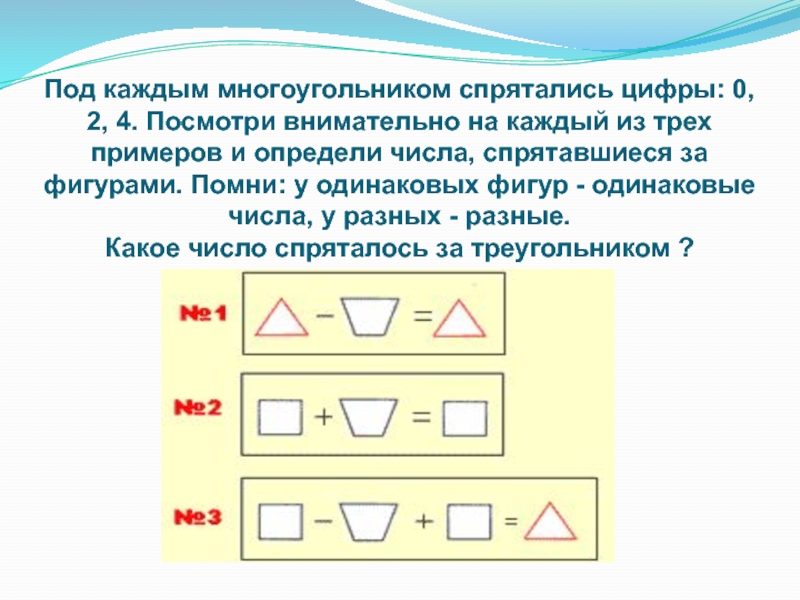
- 9. Под каждым многоугольником спрятались цифры: 0, 2,
- 10. Мой дедушка очень любит розыгрыши. Он
- 11. От Кощея Бессмертного до Кикиморы ведут три
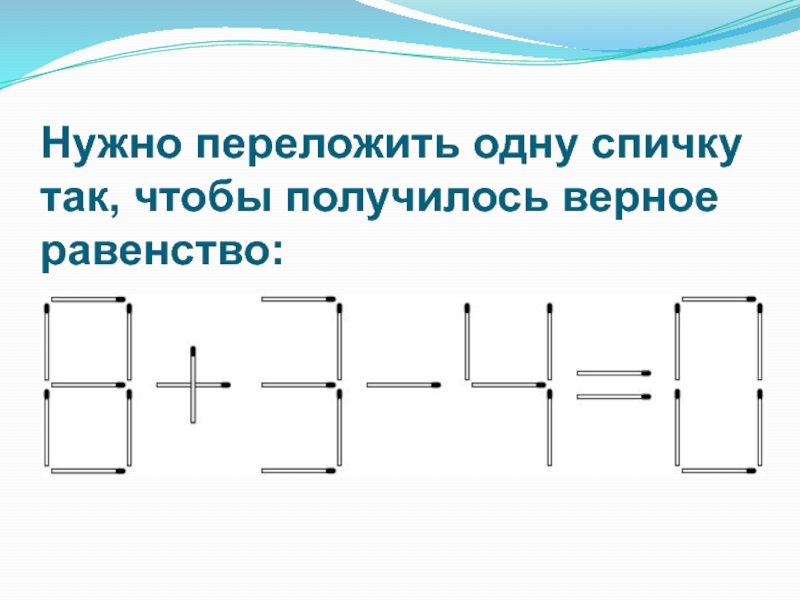
- 12. Нужно переложить одну спичку так, чтобы получилось верное равенство:
- 13. 2 метод. Придумать или объяснить задачу
- 14. Привезли 12 ящиков яблок по 30 кг
- 15. По выражению составьте задачу (50+30)*2=160
- 16. 3 метод. Использование карточек для слабоуспевающих детей
- 17. Слайд 17
- 18. Слайд 18
- 19. 4 метод. Использование мнемонические правил в математике
- 20. Правило при раскрытии скобок:Перед скобкой “плюс” стоитОн
- 21. В треугольнике, друзья,Ошибаться нам нельзя.В нем отрезки
- 22. Если верно чертеж начертил,То уже половину задачи
- 23. Раскрыв хоть книгу, хоть тетрадь,Двугранный угол встретишь
- 24. 5 метод. Использование лабораторных работ
- 25. Лабораторная работа на вывод числа пи
- 26. 6 метод. Использование практикоориентированных задач на уроках.
- 27. Обобщающий урок по теме «Прогрессии» с применением задач на тему СПИД
- 28. Какая из следующих последовательностей является арифметической прогрессией?1)
- 29. Запишите еще два члена последовательности7, 0, -7,
- 30. Выписаны первые несколько членов геометрической прогрессии:
- 31. Какое наименьшее число последовательных натуральных чисел, начиная
- 32. Каждую секунду бактерия делится на две новые
- 33. В арифметической прогрессии найдите: а25 - а15,
- 34. СПИДСиндром приобретённого иммунодефицита, иначе, более правильно, инфекция
- 35. Дана конечная арифметическая профессия (аn): Найдите n, если известны a1, d, an:..
- 36. Полученные числа показывают, какое количество людей в
- 37. Решите уравнения и выясните, какие заблуждения чаще всего связаны со СПИДом.2+5+8+…+x=222,3+7+11+…+х=820,1+5+9+...+x=120,(2+ х)+(4+х)+(6+х)+...+(30 +х)=285
- 38. 35 — передается от животных. 35
- 39. Дана геометрическая прогрессия. Найдите:
- 40. Правильным ответам соответствуют вещества, которые губят вирус
- 41. В 1999 году в Москве было 2708
- 42. 7 метод. Использование задач из ГИА и ЕГЭ на уроках в классах среднего звена
- 43. 8 метод. Дифференцированное домашнее задание.
- 44. 9 метод. Использование математических игр.
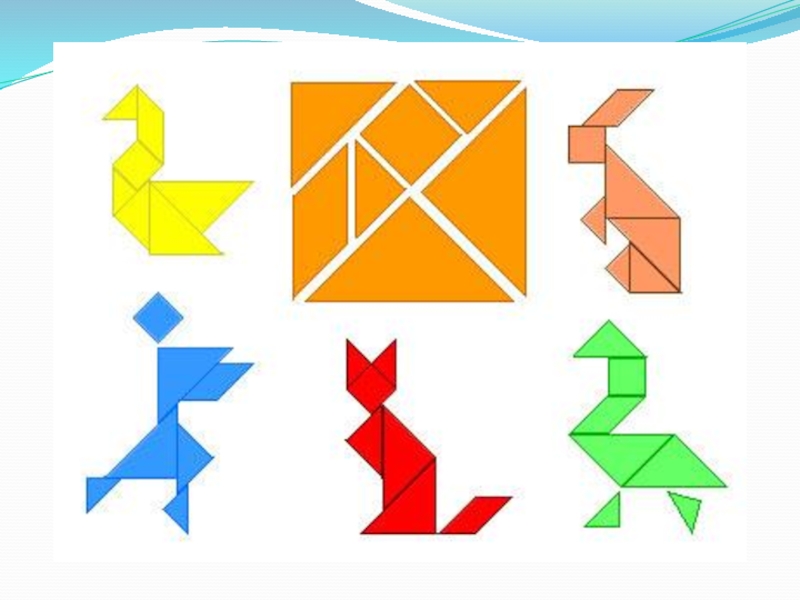
- 45. Игра “Танграм” Разрезать квадрат на семь
- 46. Слайд 46
- 47. Как играть, чтобы не проиграть На
- 48. Игра 2 (Сыграть в парах, результат фиксировать
- 49. Имеется две кучи спичек, в одной 20
- 50. На столе лежит 25 спичек. Играющие по
- 51. Выводы:Мотивация – один из факторов успешного обучения
- 52. СПАСИБО ЗА ВНИМАНИЕ!
«Все наши замыслы, все поиски и построения превращаются в прах, если у ученика нет желания учиться». В. А.Сухомлинский
Слайд 1Проблемы мотивационного характера в школьном математическом образовании
Подготовила Мостовая Д.В.
учитель математики
МБОУ
Слайд 2«Все наши замыслы, все поиски и построения превращаются в прах, если
у ученика нет желания учиться».
В. А.Сухомлинский
Слайд 4Приемы и методы, повышающие мотивацию учащихся:
Создание проблемной ситуации.
Привлечение учащихся к оценочной
деятельности
Необычная форма обучения
Разгадывание загадок, решение кроссвордов
Лабораторные работы.
Необычная форма обучения
Разгадывание загадок, решение кроссвордов
Лабораторные работы.
Слайд 5Уроки « Одной задачи»
Решение развивающих, нестандартных задач
Дифференцированные задания
Задания на самостоятельный поиск
информации
Участие в различных предметных конкурсах, предметных олимпиадах
Использование компьютерных технологий
Участие в различных предметных конкурсах, предметных олимпиадах
Использование компьютерных технологий
Слайд 9Под каждым многоугольником спрятались цифры: 0, 2, 4. Посмотри внимательно на
каждый из трех примеров и определи числа, спрятавшиеся за фигурами. Помни: у одинаковых фигур - одинаковые числа, у разных - разные.
Какое число спряталось за треугольником ?
Слайд 10Мой дедушка очень любит розыгрыши. Он закрыл дверь комнаты, где моя
бабушка хранит конфеты, на ключ. Ключ он положил в одну из коробочек, которые он замаркировал так: А, Б, В.
Затем он прикрепил записочки к каждой коробочке:
А) Ключ не в коробке Б
Б) Ключ не в этой коробке
В) Ключ в этой коробке
Бабушка сказала мне, что некоторые из этих утверждений правильные, а некоторые - ложные. Но если, не заглядывая в коробочки, я протяну дедушке коробочку, в которой будет лежать ключ, у меня будет столько конфет, сколько я захочу.
Какую коробочку надо протянуть дедушке ?
Слайд 11От Кощея Бессмертного до Кикиморы ведут три дороги (№1, №2, №3). От
Кикиморы до Бабы-Яги - 2 дороги (№4, №5).
Сколькими способами может добраться Кощей до Бабы-Яги, заходя в гости к Кикиморе ?
Слайд 14Привезли 12 ящиков яблок по 30 кг в каждом и 8
ящиков груш по 40 кг в каждом. Какой смысл имеют следующие выражения?
30*12
12-8
40*8
40-30
30*12+40*8
30*12-40*8
Слайд 20Правило при раскрытии скобок:
Перед скобкой “плюс” стоит
Он о том и говорит,
Что
ты скобки опускай,
Да все числа выпускай.
Перед скобкой “минус” строгий
Загородит нам дорогу.
Чтобы скобки убирать,
Надо знаки поменять.
Да все числа выпускай.
Перед скобкой “минус” строгий
Загородит нам дорогу.
Чтобы скобки убирать,
Надо знаки поменять.
Слайд 21В треугольнике, друзья,
Ошибаться нам нельзя.
В нем отрезки проведи,
Правильно их назови:
Биссектриса, словно
крыса,
Она лазит по углам
И делит угол пополам.
И как ласковая мама
Сторону разделит пополам
Наша Медиана.
Высота со стороной
Составят угол, да прямой.
Биссектрису, медиану, высоту
Аккуратно из вершины проведу.
Она лазит по углам
И делит угол пополам.
И как ласковая мама
Сторону разделит пополам
Наша Медиана.
Высота со стороной
Составят угол, да прямой.
Биссектрису, медиану, высоту
Аккуратно из вершины проведу.
Слайд 22Если верно чертеж начертил,
То уже половину задачи решил.
Чтобы задачу о пирамиде
решать,
В ней высоту надо вниз опускать.
Узнай, где основание той высоты,
Тогда и задачу скорее реши.
В ней высоту надо вниз опускать.
Узнай, где основание той высоты,
Тогда и задачу скорее реши.
Слайд 23Раскрыв хоть книгу, хоть тетрадь,
Двугранный угол встретишь ты опять.
А в нем
– линейные углы,
И все, конечно же, равны.
С углом линейным не шути,
Скорее строй и находи.
На ребре двугранного угла
Пусть будет точка какая – то дана.
Перпендикуляры из нее ты в гранях проведи
Линейный угол уж готов, его и находи.
И все, конечно же, равны.
С углом линейным не шути,
Скорее строй и находи.
На ребре двугранного угла
Пусть будет точка какая – то дана.
Перпендикуляры из нее ты в гранях проведи
Линейный угол уж готов, его и находи.
Слайд 28Какая из следующих последовательностей является арифметической прогрессией?
1) Последовательность натуральных степеней числа
2.
2) Последовательность натуральных чисел, кратных 5.
3) Последовательность кубов натуральных чисел.
4) Последовательность всех правильных дробей, числитель которых на 1 меньше знаменателя.
2) Последовательность натуральных чисел, кратных 5.
3) Последовательность кубов натуральных чисел.
4) Последовательность всех правильных дробей, числитель которых на 1 меньше знаменателя.
Слайд 30Выписаны первые несколько членов геометрической прогрессии: − 256; 128; − 64; … Найдите
сумму первых семи её членов.
Слайд 31Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить,
чтобы получившаяся сумма была больше 465?
Слайд 32Каждую секунду бактерия делится на две новые бактерии. Известно, что весь
объём одного стакана бактерии заполняют за 1 час. За сколько секунд бактерии заполняют половину стакана?
Слайд 33В арифметической прогрессии найдите:
а25 - а15, если d = 3;
(31- Л, 63 – С, 24-В)
d, если а7 = 47, а12 = 82; (20 - Н, 30 - П, 40 – Е)
a1 , если а30 = 205, d = 7; (54 - У, 2 -И, 27- Ч)
а20, если а1 = 7, d = 3; (7 - Д, 17 - К, 5-А)
d, если а7 = 47, а12 = 82; (20 - Н, 30 - П, 40 – Е)
a1 , если а30 = 205, d = 7; (54 - У, 2 -И, 27- Ч)
а20, если а1 = 7, d = 3; (7 - Д, 17 - К, 5-А)
Слайд 34СПИД
Синдром приобретённого иммунодефицита, иначе, более правильно, инфекция ВИЧ (вирус иммунодефицита человека).
Первые заболевшие зарегистрированы в США в 1981 году. К данному моменту СПИДом в мире болеют около 4,5 млн человек и еще 20 млн инфицированы ВИЧ.
Вирус иммунодефицита человека принадлежит к семейству ретровирусов, он может синтезировать ДНК с РНК, тогда как другие только РНК с ДНК. Вирус проникает внутрь клетки — лимфоцита, встраивается в генетический аппарат клетки и заставляет продуцировать частицы вируса до тех пор, пока клетка не погибнет. К сожалению, большинство лекарственных препаратов, оказывающих на вирус угнетающее действие, влияют аналогичным образом и на клетки организма человека.
Вирус иммунодефицита человека принадлежит к семейству ретровирусов, он может синтезировать ДНК с РНК, тогда как другие только РНК с ДНК. Вирус проникает внутрь клетки — лимфоцита, встраивается в генетический аппарат клетки и заставляет продуцировать частицы вируса до тех пор, пока клетка не погибнет. К сожалению, большинство лекарственных препаратов, оказывающих на вирус угнетающее действие, влияют аналогичным образом и на клетки организма человека.
Слайд 36Полученные числа показывают, какое количество людей в процентах заразились: СПИДом при
- половом контакте,
- употреблении наркотиков,
- переливании крови.
Сколько процентов ещё не хватает?
Ответ: 80% — заражение половым путем, 15% — при употреблении наркотиков, 3% — при переливании крови, 1 % — дети зараженных, 1% — не выяснено из-за нехватки данных
Слайд 37Решите уравнения и выясните, какие заблуждения чаще всего связаны со СПИДом.
2+5+8+…+x=222,
3+7+11+…+х=820,
1+5+9+...+x=120,
(2+
х)+(4+х)+(6+х)+...+(30 +х)=285
Слайд 38 35 — передается от животных. 35 - больной беззащитен перед любой
инфекцией.
79 - инфекция передаётся через воздух, прикосновение.
80 – имеет 100% смертность
29 - заболевание исключительно наркоманов,
3 - не имеет характерных черт.
Ответ: больные СПИДом грипп и острые респираторные заболевания переносят так же, как и другие; вирус передаётся только через кровь, от человека к человеку. Совместное проживание и общение не ведут к заражению; СПИДом обычно болеют люди, ведущие беспорядочную половую жизнь, часто меняющие партнеров; проявления СПИДа разнообразны, но хорошо изучены врачами.
Слайд 40Правильным ответам соответствуют вещества, которые губят вирус СПИДа при открытом воздействии. 32
— спирт, 10ОО — ацетон, -32 —- касторовое масло, 0,5 — гидрохлорид натрия, 2 — крем от загара, -162 — эфир,
Вирус погибает при нагревании до 57 градусов Цельсия, на поверхности кожи быстро разрушается под действием защитных ферментов организма и бактерий.
Слайд 41В 1999 году в Москве было 2708 ВИЧ-инфицированных, в 2000 году
— 8064. Если рассмотреть арифметическую прогрессию, где а1=2708, а2=8064, то можно узнать, сколько инфицированных может быть в Москве в 2003 году, в 2010 году, если тенденция сохранится?
Ответ: в 2003 — 24 132 человека, в 2010 году — 61 624.
Возможно, что эти данные не отражают реальной картины.
Слайд 45Игра “Танграм”
Разрезать квадрат на семь геометрических фигур (и из
них сложить любые плоские фигуры, а также фигуры зверей, птиц, машин и т.д.
Слайд 47Как играть, чтобы не проиграть На крайней правой клетке полоски клетчатой
бумаги стоит фишка (рис.).
За один ход каждому из двух игроков разрешается передвинуть фишку на 1 клетку влево. Проигрывает тот, кому некуда будет ходить. Кто в этой игре выигрывает — 1-й игрок или 2- й, если полоска состоит из 10 клеток; из 25 клеток?
Слайд 48Игра 2 (Сыграть в парах, результат фиксировать в тетради) На крайней правой
клетке полоски клетчатой бумаги стоит фишка (рис.).
За один ход каждому из двух игроков разрешается передвинуть фишку на 1 клетку влево. Проигрывает тот, кому некуда будет ходить. Кто в этой игре выигрывает — 1-й игрок или 2- й, если полоска состоит из 10 клеток; из 25 клеток?
Слайд 49Имеется две кучи спичек, в одной 20 спичек, в другой -
25. Каждый из двух играющих по очереди выбрасывает одну из кучек, а другую разбивает на две части. Проигравшим считается тот, кто не может сделать очередного хода из-за того, что в каждой куче осталось по одной спичке. Кто и как выиграет при правильной игре?
Слайд 50На столе лежит 25 спичек. Играющие по очереди могут взять от
одной до четырёх спичек. Кто не может сделать ход (спичек не осталось), проигрывает.
Другими словами, выигрывает взявший последнюю спичку.
Слайд 51Выводы:
Мотивация – один из факторов успешного обучения учащихся на уроках.
Снижение положительной
мотивации учащихся ведет к снижению успешности и эффективности обучения.
Использование в учебной деятельности методов и приемов современных педагогических технологий формирует положительную мотивацию детей, способствует развитию основных мыслительных операций, коммуникативной компетенции, творческой активной личности.
Использование в учебной деятельности методов и приемов современных педагогических технологий формирует положительную мотивацию детей, способствует развитию основных мыслительных операций, коммуникативной компетенции, творческой активной личности.
