- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Вычисление площади криволинейной трапеции. Алгебра и начала мат. анализа. 11 кл
Содержание
- 1. Вычисление площади криволинейной трапеции. Алгебра и начала мат. анализа. 11 кл
- 2. Слайд 2
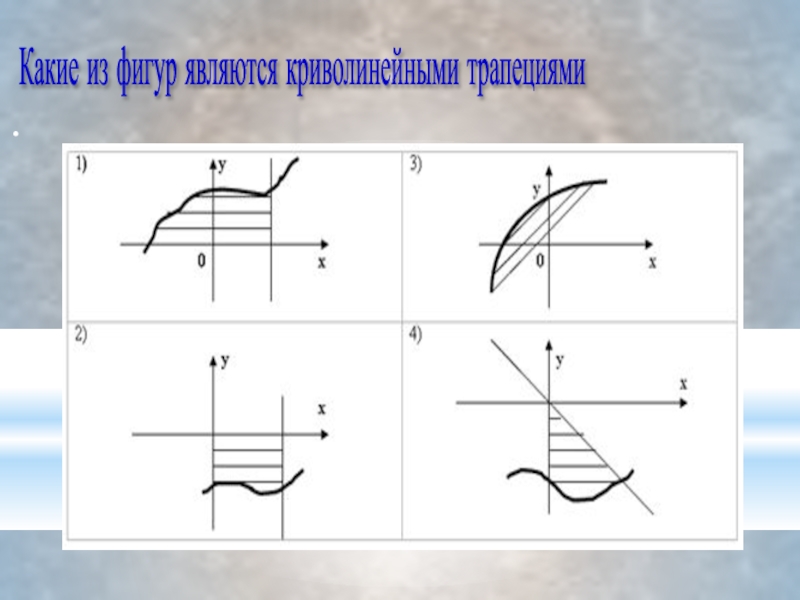
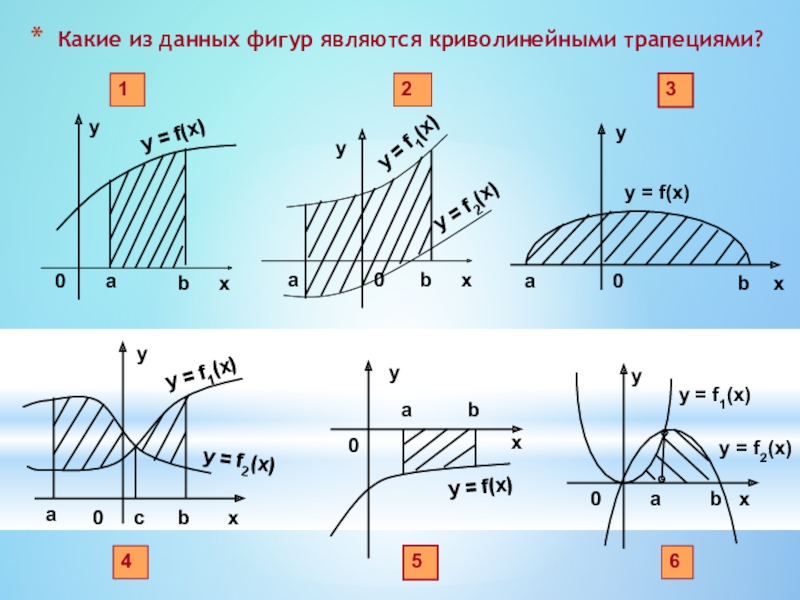
- 3. .Какие из фигур являются криволинейными трапециями
- 4. Благодаря этим знаниям
- 5. Какие из данных фигур являются криволинейными трапециями?
- 6. Слайд 6
- 7. Если f – непрерывная и
- 8. Доказательство Доказательство : Рассмотрим функцию S( x)
- 9. Выясним геометрический смысл числителя ΔS ( x)
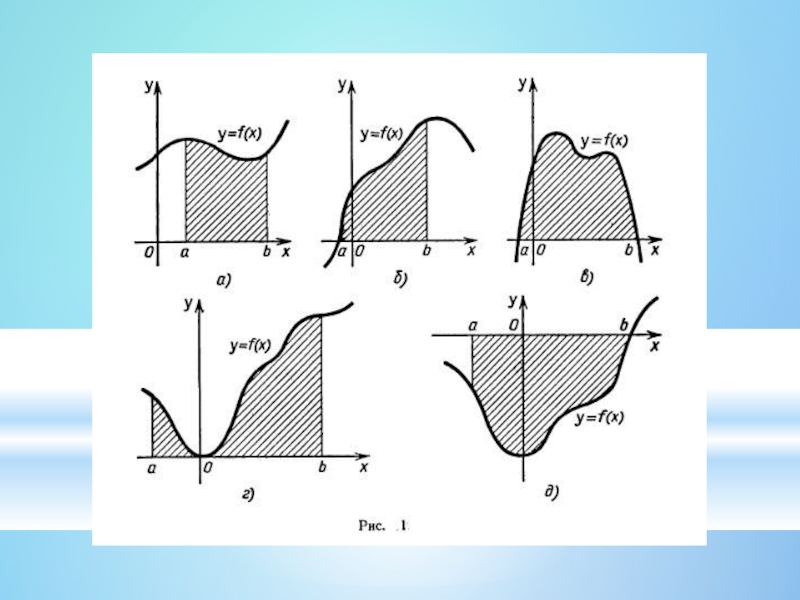
- 10. Определение О: Криволинейной трапецией называется фигура D с границейгде функция (х) непрерывна (рис. 17.1).
- 11. Теория Найдем площадь криволинейной трапеции. Для этого
- 12. Пример: Вычислить площадь криволинейной трапеции, ограниченной линиями
- 13. Связь между определенным интегралом и первообразной (Формула
- 14. Основные свойства определенного интеграла
- 15. Какая трапеция называется криволинейной ?
- 16. Решение задач
- 17. № 2F(x) = x2 + 4x +
- 18. № 3РешениеF(x) = x2 + 4x +
- 19. Построим графики функций y = x2 +
- 20. № 4РешениеНайдем уравнение касательных к графику функции
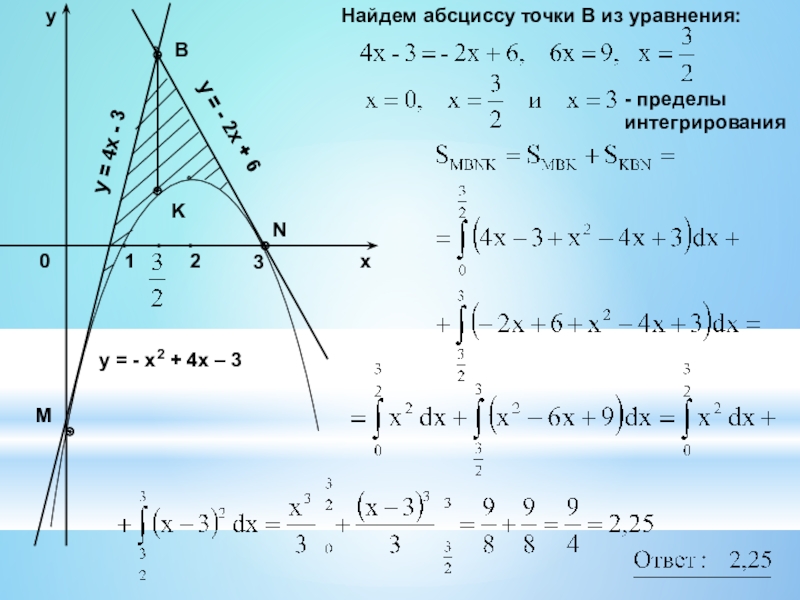
- 21. Найдем абсциссу точки В из уравнения:- пределы интегрированияK
- 22. Решаем задачи № 5
- 23. Задача № 6
- 24. № 7Вычислить:1 способНа [-2; 2], |x
- 25. 2 способТ.к. функция у = |х
- 26. Самостоятельная работа
Слайд 1ГБОУ средняя общеобразовательная школа с.Надеждино
Алгебра 11 класс
Площадь
криволинейной
трапеции
Учитель математики –
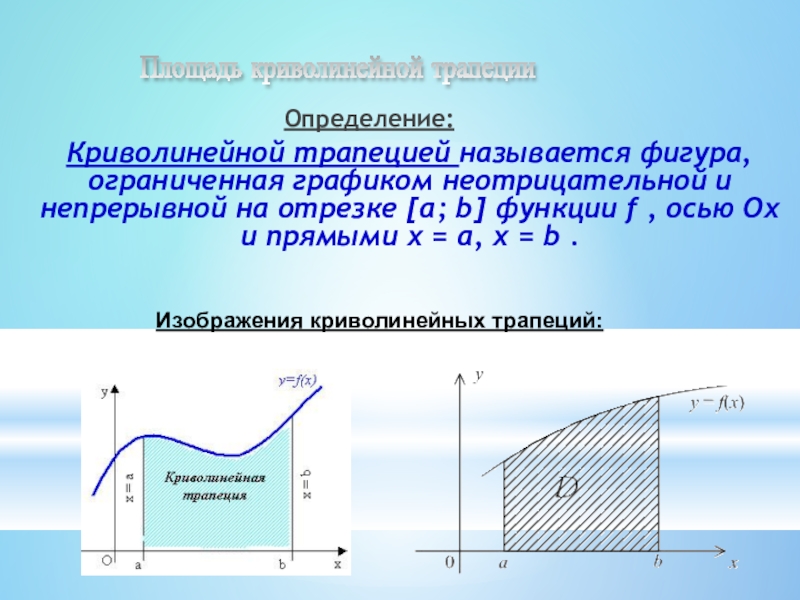
Слайд 2
Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a; b] функции f , осью Ох и прямыми х = а, х = b .
Площадь криволинейной трапеции
Изображения криволинейных трапеций:
Слайд 4 Благодаря этим знаниям математики в былые времена
Сейчас эту площадь можно посчитать с хорошей степенью точности, используя методы математических вычислений, но это не освобождает от знаний основ математического анализа, на основании которых эти методы строятся.
Отступление
Слайд 7
Если f – непрерывная и неотрицательная на отрезке [a;
Теорема:
Теорема о вычислении площади криволинейной трапеции
Слайд 8Доказательство
Доказательство : Рассмотрим функцию S( x) , определенную на
отрезке [a;
криволинейной трапеции , которая расположена левее вертикальной
прямой , проходящей через точку М ( x: 0 ) ( рис 2.а)
Если x = a , то S ( a ) = o . Отметим , что S ( b) = S ( S – площадь
криволинейной трапеции ) .
Нам осталось доказать , что S' ( x ) = f ( x ) (2)
По определению производной
докажем, что ΔS(x) → f ( x ) (3)
Δ x
при Δ x →0
Слайд 9
Выясним геометрический смысл числителя ΔS ( x) . Для простоты
рассмотрим случай
то ΔS ( x) – площадь фигуры , заштрихованной на рисунке 2, б.
Дальнейшее доказательство рассмотрите самостоятельно.
Итак , мы получили, что S есть первообразная для f . Поэтому
в силу основного свойства первообразных для всех x, принадлежащих
промежутку [ a ; b ] . имеем :
S ( x ) = F (x) + C ,
где C – некоторая постоянная , а F – одна из первообразных
для функции F . Для нахождения C подставим х = а :
F ( a ) + C = S ( a ) = 0,
откуда C = - F (a ) . Следовательно ,
S ( x ) = F( x ) – F ( a ). (4)
Поскольку площадь криволинейной трапеции
равна S ( b ) , подставляя x = b в формулу ( 4 ) ,
получим:
S = S ( b ) = F ( b ) – F ( a ).
Доказательство
Слайд 10Определение
О: Криволинейной трапецией называется фигура D с границей
где функция (х)
Слайд 11Теория
Найдем площадь криволинейной трапеции. Для этого разобьем отрезок [а, b]
на элементарных отрезков
Обозначим выберем произвольные точки и построим ступенчатую фигуру из прямоугольников с высотами и основаниями Площадь ступенчатой фигуры и дает приближенное значение площади криволинейной трапеции. За точное значение площади естественно принять
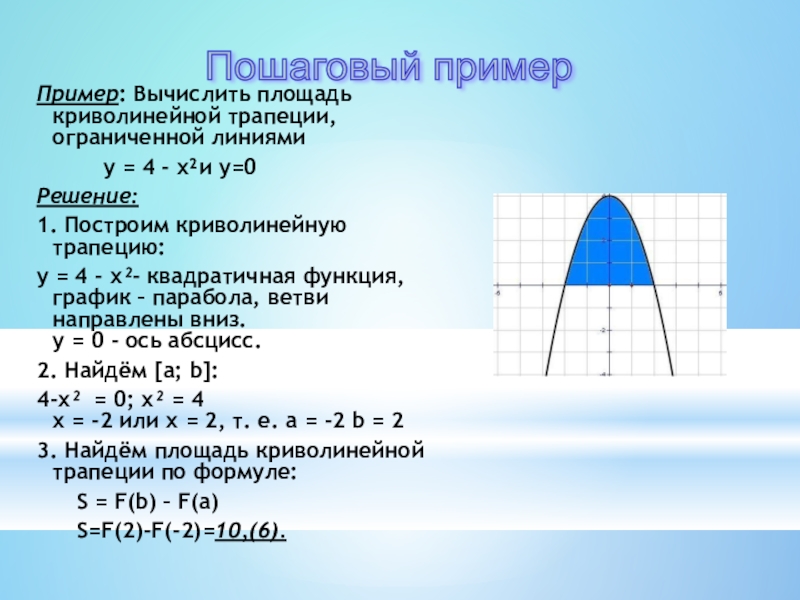
Слайд 12Пример: Вычислить площадь криволинейной трапеции, ограниченной линиями
Решение:
1. Построим криволинейную трапецию:
у = 4 - х²- квадратичная функция, график – парабола, ветви направлены вниз. у = 0 - ось абсцисс.
2. Найдём [а; b]:
4-х² = 0; х² = 4 х = -2 или х = 2, т. е. а = -2 b = 2
3. Найдём площадь криволинейной трапеции по формуле:
S = F(b) – F(а)
S=F(2)-F(-2)=10,(6).
Пошаговый пример
Слайд 13Связь между определенным интегралом и первообразной
(Формула Ньютона - Лейбница)
Для непрерывной функции
где
Слайд 15Какая трапеция называется криволинейной ? (определение вместе с рисунком).
Может ли быть функция f отрицательной на отрезке [a; b]? Почему?
Определение первообразной.
Правила нахождения первообразных.
Если f – … на отрезке [a; b] функция , а F – ее первообразная на этом отрезке , то площадь S соответствующей криволинейной трапеции равна … ? Чему?
Контрольные вопросы
Слайд 17№ 2
F(x) = x2 + 4x + С – общий вид
Найдем С:
1 способ
Если х = 1, то F(1) = 9, А (1; 9) – точка касания
т.е. F(1) = 1 + 4 +С = 9.
5 + С = 9, С = 4
Найти первообразную функции f(x) = 2x + 4, график которой проходит через точку А(1,9)
Решение
№ 345
Слайд 18№ 3
Решение
F(x) = x2 + 4x + c – общий вид
Найдем с:
1 способ
Т.к. график функции F касается прямой у = 6х + 3, то по геометрическому смыслу производной F ’(x) = k, F ‘(x) = 6, 2x + 4 = 6, x = 1.
Если х = 1, то у = 6 + 3 = 9. А (1; 9) – точка касания.
Т.к. парабола проходит через т.А, то F(1) = 9
F(1) = 1 + 4 + c = 5 + c, 5 + c = 9, c = 4
2 способ
Т.к. парабола и касательная имеют только одну общую точку, то уравнение x2 + 4x + c = 6х + 3 имеет единственный корень (D = 0), тогда
x2 – 2x + c – 3 = 0
D1 = 1 – c + 3 = - с + 4, - с + 4 = 0, с = 4
Следовательно, F(x) = x2 + 4x + 4
а) Найти первообразную функции f(x) = 2x + 4, график которой касается прямой у = 6х + 3.
б)Вычислить площадь фигуры, ограниченной графиком найденной первообразной и прямыми у = 6х + 3, у = 0.
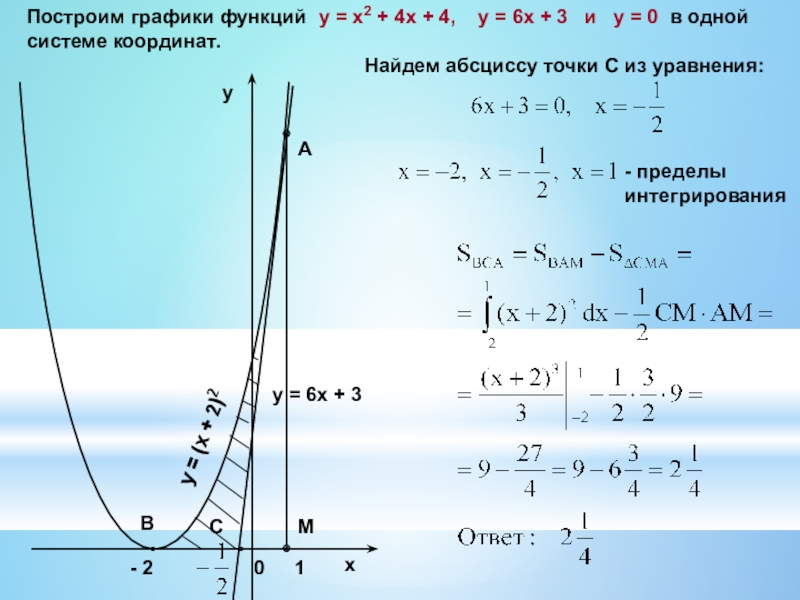
Слайд 19Построим графики функций y = x2 + 4x + 4,
Найдем абсциссу точки С из уравнения:
- пределы интегрирования
Слайд 20№ 4
Решение
Найдем уравнение касательных к графику функции f(x) = - x2
y = f(x0) + f ‘(x0)(x – x0) – уравнение касательной в общем виде
Вычислить площадь фигуры, ограниченной параболой
у = - х2 + 4х – 3 и касательными к ней в точках с абсциссами
х = 0 и х = 3.
x0 = 0
1) f(0) = - 3
2) f ‘(x) = - 2x + 4
3) f ‘(0) = 4
4) y = - 3 + 4(x – 0)
y = 4x – 3
x0 = 3
1) f(3) = - 9 + 12 – 3 = 0
2) f ‘(3) = - 2
3) y = - 2(x – 3)
y = - 2x + 6
Построим графики функций у = - х2 + 4х – 3, y = 4x – 3, y = - 2x + 6 в одной системе координат:
у = - х2 + 4х – 3 – графиком является парабола. (2; 1) – вершина параболы

![Вычисление площади криволинейной трапеции. Алгебра и начала мат. анализа. 11 кл Если f – непрерывная и неотрицательная на отрезке [a; b] Если f – непрерывная и неотрицательная на отрезке [a; b] функция , а F –](/img/thumbs/36217df499d3dd83c929e9c2ade71de0-800x.jpg)
![Вычисление площади криволинейной трапеции. Алгебра и начала мат. анализа. 11 кл Доказательство Доказательство : Рассмотрим функцию S( x) , определенную наотрезке [a; Доказательство Доказательство : Рассмотрим функцию S( x) , определенную наотрезке [a; b] . Если a < x](/img/thumbs/53e66dc8349941ec0a7dcae159e67cca-800x.jpg)


![Вычисление площади криволинейной трапеции. Алгебра и начала мат. анализа. 11 кл Теория Найдем площадь криволинейной трапеции. Для этого разобьем отрезок [а, b] Теория Найдем площадь криволинейной трапеции. Для этого разобьем отрезок [а, b] точками](/img/thumbs/f2e4bcf650222716b7c7592391fabb48-800x.jpg)









![Вычисление площади криволинейной трапеции. Алгебра и начала мат. анализа. 11 кл № 7Вычислить:1 способНа [-2; 2], |x – 2| = - x № 7Вычислить:1 способНа [-2; 2], |x – 2| = - x + 2На (2; 3],](/img/thumbs/c4a46d3f92785b05b42dc34d1bc45502-800x.jpg)