- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Внеклассное мероприятие Математика в Древнем Египте
Содержание
- 1. Внеклассное мероприятие Математика в Древнем Египте
- 2. Применялась математика в Древнем Египте очень часто
- 3. К огромному сожалению, у современного человека очень
- 4. ИсточникиОсновные сохранившиеся источники относятся к периоду Среднего царства, времени расцвета древнеегипетской культуры:
- 5. Все задачи из папируса Ахмеса (записан ок.
- 6. Нумерация (запись чисел)Древнеегипетская нумерация, то есть запись
- 7. Иероглифы для изображения чисел
- 8. Пример записи дробей из Папируса Ринда
- 9. АрифметикаЗнаки сложения и вычитанияЧтобы показать знаки сложения
- 10. АрифметикаУмножениеДревнеегипетское умножение является последовательным методом умножения двух
- 11. ГеометрияРеконструкция водяных часов по чертежам из Оксиринха
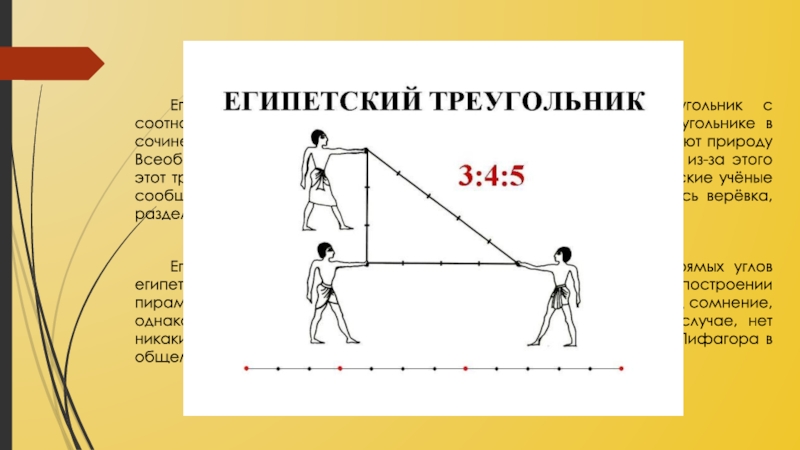
- 12. ГеометрияЕгипетским треугольником называется прямоугольный треугольник с соотношением
- 13. Вывод о математике во времена Древнего египтаК
- 14. Благодарю за внимание…
Слайд 1Внеклассное мероприятие
Математика в Древнем Египте
Выполнил работу:
учитель математики
Киричевский А.Р.
Слайд 2Применялась математика в Древнем Египте очень часто и в основном в
Развитие математики в Древнем Египте
В Египте математика использовалась еще с самых древних времен, что подтверждается различными текстами, которые относятся к началу второго тысячелетия до н.э.
Слайд 3К огромному сожалению, у современного человека очень мало сведений о древнеегипетской
Слайд 4Источники
Основные сохранившиеся источники относятся к периоду Среднего царства, времени расцвета древнеегипетской
Слайд 5Все задачи из папируса Ахмеса (записан ок. 1650 года до н.
Слайд 6Нумерация (запись чисел)
Древнеегипетская нумерация, то есть запись чисел, была похожа на
Любое число в Древнем Египте можно было записать двумя способами: словами и цифрами. Например, чтобы написать число 30, можно было использовать обычные иероглифы:
или то же самое написать цифрами (три символа десятки):
– Иероглифическая запись числа 35736
Слайд 9Арифметика
Знаки сложения и вычитания
Чтобы показать знаки сложения или вычитания использовался иероглиф
Если направление ног у этого иероглифа совпадало с направлением письма, тогда он означал «сложение», в других случаях он означал «вычитание».
Сложение
Если при сложении получается число большее десяти, тогда десяток записывается повышающим иероглифом.
1. Например: 2343 + 1671
+ 2. Собираем все однотипные иероглифы вместе:
3. Преобразуем:
4. Окончательный результат:
Слайд 10Арифметика
Умножение
Древнеегипетское умножение является последовательным методом умножения двух чисел. Чтобы умножать числа,
Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное перемножение на второй множитель.
Этот метод можно и сегодня встретить в очень отдаленных регионах.
Разложение
Египтяне использовали систему разложения наименьшего множителя на кратные числа, сумма которых составляла бы исходное число.
Чтобы правильно подобрать кратное число, нужно было знать следующую таблицу значений:
1 x 2 = 2
2 x 2 = 4
4 x 2 = 8
8 x 2 = 16
16 x 2 = 32
Пример разложения числа 25:
Кратный множитель для числа «25» — это 16.
25 — 16 = 9,
Кратный множитель для числа «9» — это 8,
9 — 8 = 1,
Кратный множитель для числа «1» — это 1,
1 — 1 = 0
Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1.
Пример: умножим «13» на «238»:
1 х 238 = 238
4 х 238 = 952
8 х 238 = 1904
13 х 238 = 3094
Известно, что 13 = 8 + 4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: 13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 3094
Уравнения
Пример задачи из папируса Ахмеса:
Найти число, если известно, что от прибавления к нему 2/3 его и вычитания из результата его трети получается 10.
Слайд 12Геометрия
Египетским треугольником называется прямоугольный треугольник с соотношением сторон 3:4:5. Плутарх в
Египетский треугольник активно применялся для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид. Историк Ван дер Варден попытался поставить этот факт под сомнение, однако более поздние исследования его подтвердили. В любом случае, нет никаких свидетельств, что в Древнем Египте была известна теорема Пифагора в общем случае (в отличие от Древнего Вавилона).
Слайд 13Вывод о математике во времена Древнего египта
К сожалению полностью отсутствуют какие
Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём индуктивных обобщений и гениальных догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что математика в Древнем Египте тех лет имела или, по крайней мере, начинала приобретать теоретический характер. Так, египетские математики умели извлекать корни (целочисленные) и возводить в степень, решать уравнения, были знакомы с арифметической и геометрической прогрессией и даже владели зачатками алгебры: при решении уравнений специальный иероглиф «куча» обозначал неизвестное.