- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок по теме “Бесконечно убывающая геометрическая прогрессия” (алгебра, 10кл.)
Содержание
- 1. Урок по теме “Бесконечно убывающая геометрическая прогрессия” (алгебра, 10кл.)
- 2. I. Арифметическая и геометрическая прогрессии. Вопросы1.
- 3. II. Арифметическая прогрессия. ЗаданияАрифметическая прогрессия задана
- 4. II. Геометрическая прогрессия. Задания5. Для геометрической
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. определение:Геометрическая прогрессия называетсябесконечно убывающей, если модуль еёзнаменателя меньше единицы.
- 9. Задача №1 Является ли последовательность бесконечно
- 10. Слайд 10
- 11. Сумма бесконечно убывающей геометрической прогрессии есть предел
- 12. Выполнение заданийНайти сумму бесконечно убывающей геометрической прогрессии с первым членом 3, вторым 0,3.2. 4.38
- 13. С какой последовательностью сегодня познакомились?Дайте определение бесконечно
- 14. На дом:1. Читать 4.4 ,4.52. №4.39
- 15. Известный польский математик Гуго Штейнгаус шутливо утверждает,
Слайд 2I. Арифметическая и геометрическая прогрессии. Вопросы
1. Определение арифметической прогрессии.
Арифметической прогрессией
2. Формула n-го члена арифметической прогрессии.
3. Формула суммы первых n членов арифметической прогрессии .
4. Определение геометрической прогрессии.
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число
5. Формула n-го члена геометрической прогрессии.
6. Формула суммы первых n членов геометрической прогрессии .
Слайд 3II. Арифметическая прогрессия.
Задания
Арифметическая прогрессия задана формулой an = 7 –
Найдите a10.
(-33)
2. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите a4 .
(4)
3. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите a17.
(-35)
4. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите S17.
(-187)
Слайд 4II. Геометрическая прогрессия.
Задания
5. Для геометрической прогрессии
найдите пятый член
6. Для геометрической прогрессии
найдите n-й член.
7. В геометрической прогрессии b3 = 8 и b5 = 2.
Найдите b4.
(4)
8. В геометрической прогрессии b3 = 8 и b5 = 2.
Найдите b1 и q.
9. В геометрической прогрессии b3 = 8 и b5 = 2.
Найдите S5.
(62)
Слайд 8определение:
Геометрическая прогрессия называется
бесконечно убывающей, если модуль её
знаменателя меньше единицы.
Слайд 9Задача №1
Является ли последовательность бесконечно убывающей геометрической прогрессией, если
Решение: а)
данная геометрическая прогрессия является бесконечно убывающей.
б)
данная последовательность не является бесконечно убывающей
геометрической прогрессией.
Слайд 11
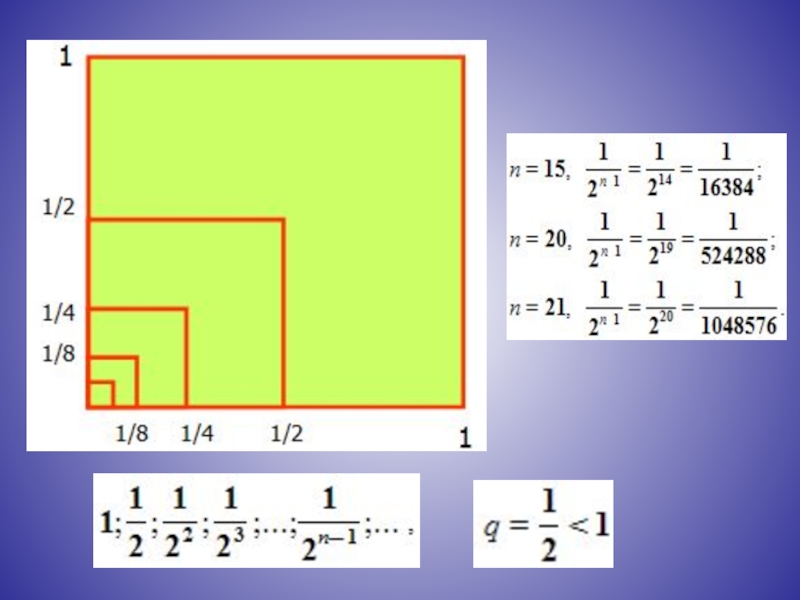
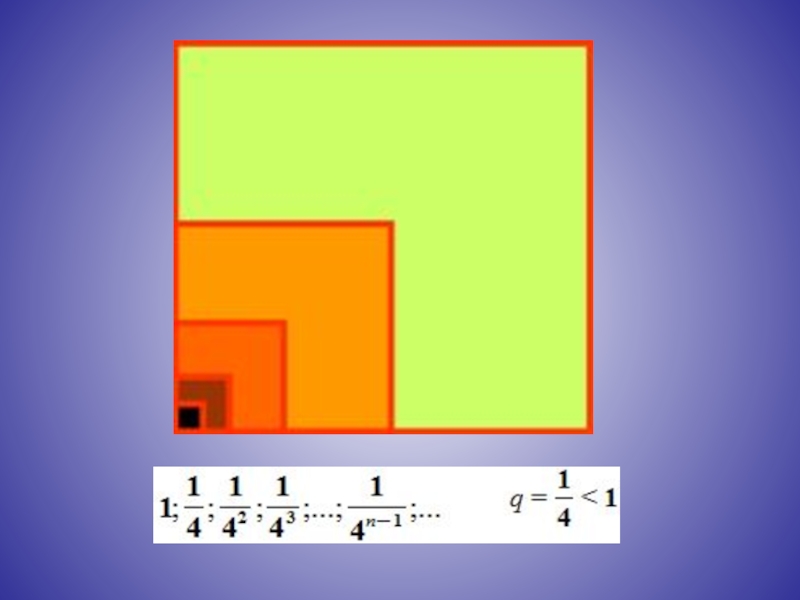
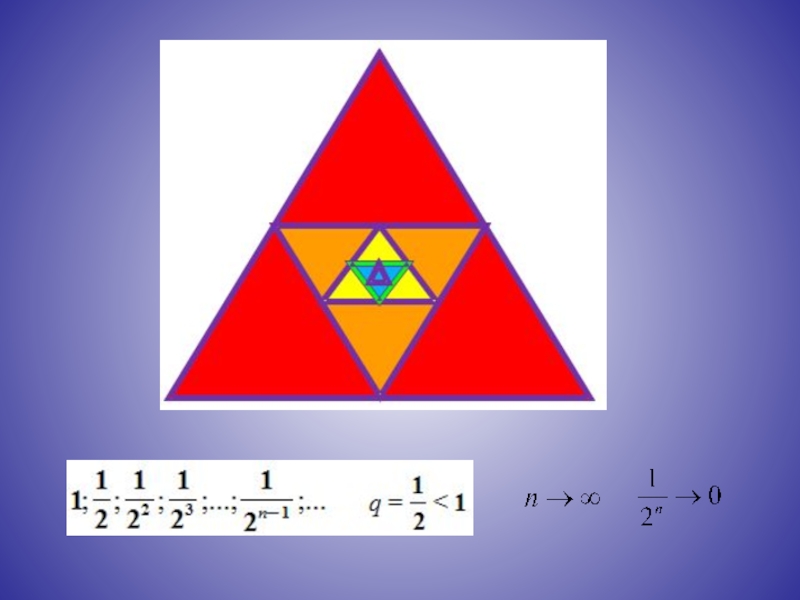
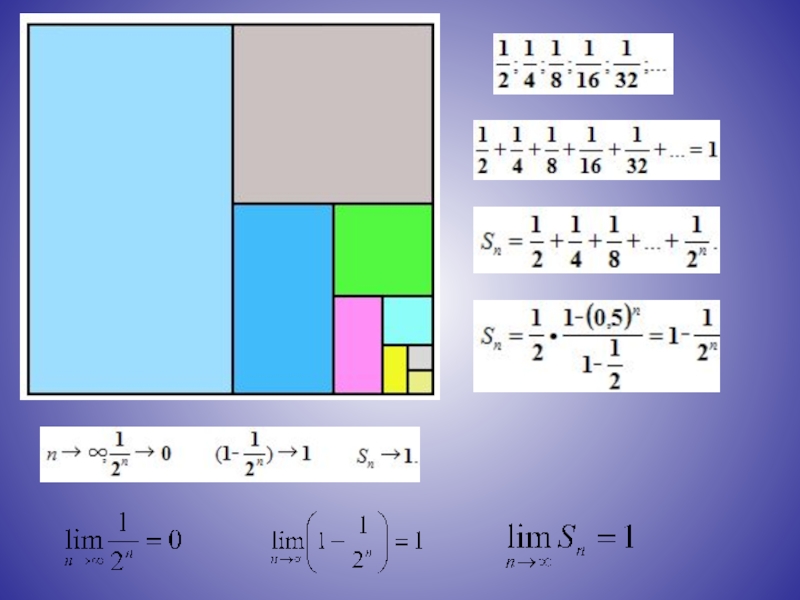
Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3,
Например, для прогрессии
имеем
Так как
Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле
Слайд 12Выполнение заданий
Найти сумму бесконечно убывающей геометрической
прогрессии с первым членом
2. 4.38
Слайд 13С какой последовательностью сегодня познакомились?
Дайте определение бесконечно убывающей геометрической прогрессии.
Как доказать,
Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
Вопросы
Слайд 15Известный польский математик Гуго Штейнгаус шутливо утверждает, что существует закон, который
Гуго Штейнгаус
14.01.1887-25.02.1972