- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок-игра по теме Производная и ее применение
Содержание
- 1. Урок-игра по теме Производная и ее применение
- 2. Цели урока:обобщение и закрепление знаний, умений и
- 3. Юбилейный паркТГК-2ТРЦ «РИО»
- 4. Ребусы
- 5. Применение производной в медицинеПрименение дифференциального исчисления в
- 6. Задача. В результате значительной потери крови содержание
- 7. Задача Предположим, что х обозначает дозу назначенного
- 8. Блиц-опросСформулируйте определение производной функции в точке.В чём
- 9. Блиц-опрос10. Найдите производную функций: y = 3х2
- 10. Применение производной в географииПроизводная помогает рассчитать:Некоторые значения
- 11. Применение производной в географииПроизводная помогает рассчитать:Некоторые значения
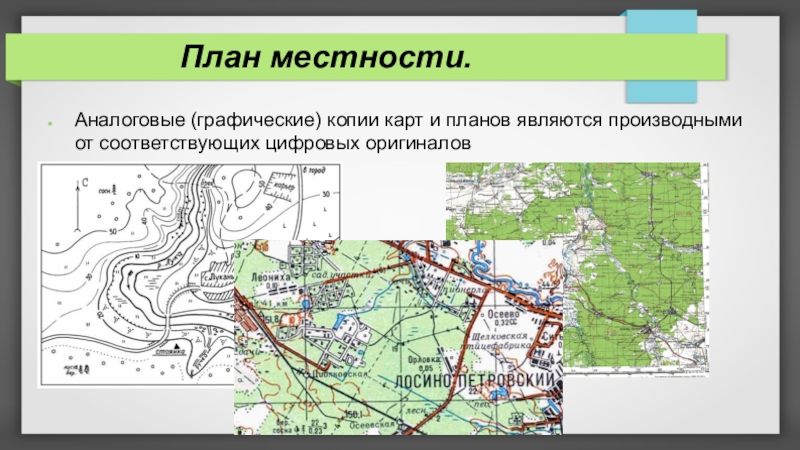
- 12. План местности.Аналоговые (графические) копии карт и планов являются производными от соответствующих цифровых оригиналов
- 13. Численность населения.Идея социологической модели Томаса Мальтуса состоит
- 14. Рост численности населенияВывести формулу для вычисления численности
- 15. ИнтерполяцияИнтерполяцией называется приближенное вычисление значений функции по
- 16. Интерполяционная формула Лагранжа.Эта формула помогает найти многочлен
- 17. Вывод: производная в географии совмещается с многими
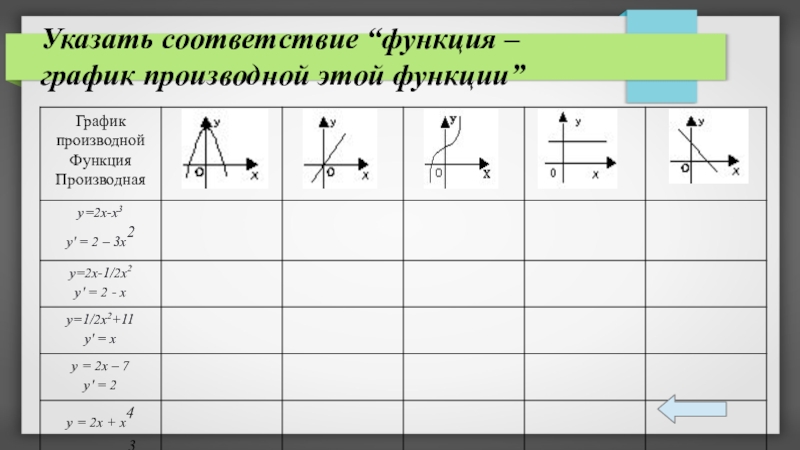
- 18. Указать соответствие “функция – график производной этой функции”
- 19. «Ситуации в жизни бывают такие: либо
- 20. Ситуация 2. После старта конькобежец в хорошем
- 21. А сейчас, команды, стоп – «Математический калейдоскоп!»
- 22. Шуточные вопросы:Кто жужжит в дисководе? Какое зерно
- 23. Итоговая таблица
- 24. Спасибо за участие!
Цели урока:обобщение и закрепление знаний, умений и навыков по теме «Производная и ее применение»воспитание коммуникативных отношений с одногруппниками; развитие логического мышления, быстроты реакции, внимания.
Слайд 2Цели урока:
обобщение и закрепление знаний, умений и навыков по теме «Производная
и ее применение»
воспитание коммуникативных отношений с одногруппниками;
развитие логического мышления, быстроты реакции, внимания.
воспитание коммуникативных отношений с одногруппниками;
развитие логического мышления, быстроты реакции, внимания.
Слайд 5Применение производной в медицине
Применение дифференциального исчисления в медицине сводится к вычислению
скорости. Например, скорости восстановительных реакций и скорости релаксационного процесса.
Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, изменении температуры тела, изменении пульса или других физиологических показателей. Степень реакции зависит от назначенного лекарства, его дозы. С помощью производной можно вычислить, при какой дозе лекарства реакция организма максимальна. С помощью второй производной можно определить условия, при которых скорость процесса наиболее чувствительна к каким-либо воздействиям
Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, изменении температуры тела, изменении пульса или других физиологических показателей. Степень реакции зависит от назначенного лекарства, его дозы. С помощью производной можно вычислить, при какой дозе лекарства реакция организма максимальна. С помощью второй производной можно определить условия, при которых скорость процесса наиболее чувствительна к каким-либо воздействиям
Слайд 6Задача. В результате значительной потери крови содержание железа в крови уменьшилось
на 210 мг. Недостаток железа вследствие его восстановления с течением времени t уменьшается по закону у=210е-t/7 мг(t – сутки). Найти зависимость скорости восстановления железа в крови от времени. Вычислить эту скорость в момент t=0 и через 7 суток.
Решение: Скорость восстановления железа: y/=-1/7·210 е-t/7=-30е-t/7
Знак «-» указывает на уменьшение недостачи. При t=0 скорость восстановления равна 30 мг/сутки. Через 7 суток скорость восстановления равна 11,1 мг/сут: y/(7)=30e-1=11,1
Релаксационный процесс – это процесс возвращения системы к состоянию устойчивого равновесия, из которого она была выведена. Во многих случаях (особенно при однократном воздействии) этот процесс описывается экспоненциальным уравнением y=y0et/τ , где τ– постоянная времени. Ее физический смысл: - это время, в течение которого начальное отклонение y0 уменьшается в e раз (т. е. в 2,7 раза). В нашей задаче постоянная времени – 7 суток.
Решение: Скорость восстановления железа: y/=-1/7·210 е-t/7=-30е-t/7
Знак «-» указывает на уменьшение недостачи. При t=0 скорость восстановления равна 30 мг/сутки. Через 7 суток скорость восстановления равна 11,1 мг/сут: y/(7)=30e-1=11,1
Релаксационный процесс – это процесс возвращения системы к состоянию устойчивого равновесия, из которого она была выведена. Во многих случаях (особенно при однократном воздействии) этот процесс описывается экспоненциальным уравнением y=y0et/τ , где τ– постоянная времени. Ее физический смысл: - это время, в течение которого начальное отклонение y0 уменьшается в e раз (т. е. в 2,7 раза). В нашей задаче постоянная времени – 7 суток.
Слайд 7Задача Предположим, что х обозначает дозу назначенного лекарства, у - функция
степени реакции. у=f(x)=x²(a-x), где а - некоторая положительная постоянная. При каком значении х реакция максимальна?
Решение: 0Тогда f/(x)=0 при x=2a/3.
Найдем вторую производную f// и ее значение в точке х=2а/3.
f//(х)=2a-6x
f//(2a/3)=2a-6·2а/3=-2а.
Значит х=2а/3 - тот уровень дозы, который дает максимальную реакцию.
Решение: 0
Найдем вторую производную f// и ее значение в точке х=2а/3.
f//(х)=2a-6x
f//(2a/3)=2a-6·2а/3=-2а.
Значит х=2а/3 - тот уровень дозы, который дает максимальную реакцию.
Слайд 8Блиц-опрос
Сформулируйте определение производной функции в точке.
В чём состоит геометрический смысл производной?
Сформулируйте
признак возрастания (признак убывания) функции.
Какую точку называют критической точкой функции?
Сформулируйте признак максимума функции.
Сформулируйте признак минимума функции.
Что такое область определения функции?
Чему равна производная любого числа?
Как найти производную степенной функции хn ?
Какую точку называют критической точкой функции?
Сформулируйте признак максимума функции.
Сформулируйте признак минимума функции.
Что такое область определения функции?
Чему равна производная любого числа?
Как найти производную степенной функции хn ?
Слайд 9Блиц-опрос
10. Найдите производную функций:
y = 3х2 + 7.
y
= х-5 + √2х.
y = sinх + π.
y = x7 – 4x5.
y = cos3x – 2ех.
y = (2x – 7)3.
y = sin2x + cos2x .
y = ln(x2+2х) - е2х-7
y = sinх + π.
y = x7 – 4x5.
y = cos3x – 2ех.
y = (2x – 7)3.
y = sin2x + cos2x .
y = ln(x2+2х) - е2х-7
Слайд 10Применение производной в географии
Производная помогает рассчитать:
Некоторые значения в сейсмографии
Особенности электромагнитного поля
земли
Радиоактивность ядерно-геофизических показателей
Многие значения в экономической географии
Радиоактивность ядерно-геофизических показателей
Многие значения в экономической географии
Слайд 11Применение производной в географии
Производная помогает рассчитать:
Некоторые значения в сейсмографии
Особенности электромагнитного поля
земли
Радиоактивность ядерно-геофизических показателей
Многие значения в экономической географии
Вывести формулу для вычисления численности населения на территории в момент времени t.
Радиоактивность ядерно-геофизических показателей
Многие значения в экономической географии
Вывести формулу для вычисления численности населения на территории в момент времени t.
Слайд 12План местности.
Аналоговые (графические) копии карт и планов являются производными от соответствующих
цифровых оригиналов
Слайд 13Численность населения.
Идея социологической модели Томаса Мальтуса состоит в том, что прирост
населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.
Слайд 14Рост численности населения
Вывести формулу для вычисления численности населения на ограниченной территории
в момент времени t.
Решение: Пусть у = у(t)- численность населения.
Рассмотрим прирост населения за Dt = t-t0
Dy = k y Dt, где к = кр – кс –коэффициент прироста (кр – коэффициент рождаемости,
кс – коэффициент смертности)
Dy:Dt=k y
При Dt→0 получим lim Dy/ Dt=у’
у’= к у
Решение: Пусть у = у(t)- численность населения.
Рассмотрим прирост населения за Dt = t-t0
Dy = k y Dt, где к = кр – кс –коэффициент прироста (кр – коэффициент рождаемости,
кс – коэффициент смертности)
Dy:Dt=k y
При Dt→0 получим lim Dy/ Dt=у’
у’= к у
Слайд 15Интерполяция
Интерполяцией называется приближенное вычисление значений функции по нескольким данным ее значениям.
Интерполяция широко используется в картографии, геологии, экономике и других науках. Самым простым вариантом интерполяции является форма Лагранжа, но когда узловых точек много и интервалы между ними велики, либо требуется получить функцию, кривизна которой минимальна.
Слайд 16Интерполяционная формула Лагранжа.
Эта формула помогает найти многочлен степени n по известным
его значениям с i по n+1
Пример 1
Пример 1
Слайд 17Вывод: производная в географии совмещается с многими ее отраслями( сейсмография, размещение
и численность населения) а также с экономической географии. Все это позволяет полнее изучать развитие населения и стран мира.
Слайд 19«Ситуации в жизни бывают такие:
либо сложные, либо простые…»
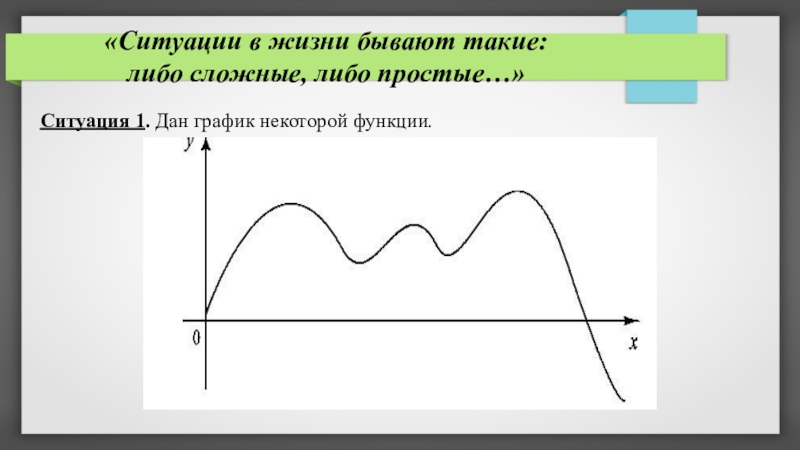
Ситуация 1.
Дан график некоторой функции.
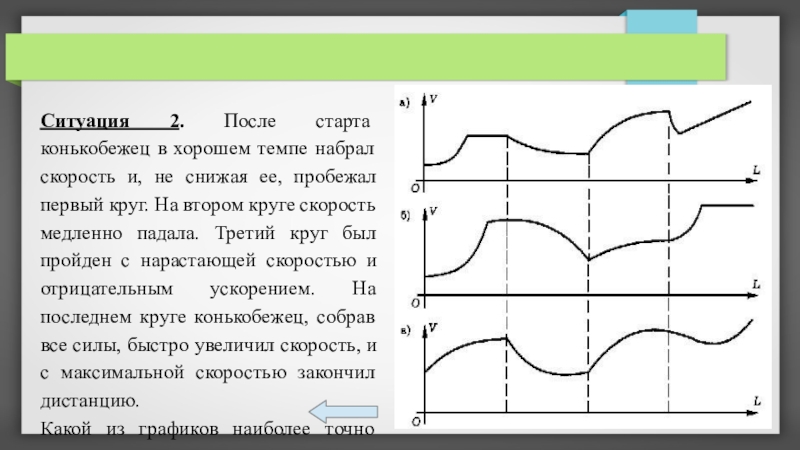
Слайд 20Ситуация 2. После старта конькобежец в хорошем темпе набрал скорость и,
не снижая ее, пробежал первый круг. На втором круге скорость медленно падала. Третий круг был пройден с нарастающей скоростью и отрицательным ускорением. На последнем круге конькобежец, собрав все силы, быстро увеличил скорость, и с максимальной скоростью закончил дистанцию.
Какой из графиков наиболее точно отражает описанную ситуацию?
Какой из графиков наиболее точно отражает описанную ситуацию?
Слайд 21А сейчас, команды, стоп – «Математический калейдоскоп!» Кто в терминах не знает затрудненья,
Их назовет нам все без промедленья.
Любой участник поочередно от каждой команды называет на букву П математические термин
Любой участник поочередно от каждой команды называет на букву П математические термин
Слайд 22Шуточные вопросы:
Кто жужжит в дисководе?
Какое зерно интересует программиста?
Почему у
программистов хронический насморк и кашель?
«Открой окошко – разорю тебя немножко». О чём это?
Почему кошки очень любят лизать руки программистам?
«Открой окошко – разорю тебя немножко». О чём это?
Почему кошки очень любят лизать руки программистам?