- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Умножение
Содержание
- 1. Умножение
- 2. Смысл действия умножения Действие умножения рассматривается как
- 3. Прежде, чем знакомиться с символикой записи действий
- 4. Виды заданий, которые предлагаются детям до знакомства
- 5. Виды заданий, используемых для усвоения ребенком
- 6. Виды заданий, используемых для усвоения ребенком
- 7. Виды заданий, используемых для усвоения ребенком
- 8. Выражение вида 3 • 5 называют произведением.
- 9. Среди данных выражений найдите такие,
- 10. Если произведение разделить на один множитель, то
- 11. Правило проверки действия умножения: Произведение делят на
- 12. Табличное умножение Изучение таблицы умножения является центральной
- 13. При значении второго множителя больше 5 для
- 14. Прием перестановки множителей Этот прием фактически является
- 15. Составление двух первых таблиц распределяется на
- 16. При составлении таблицы умножения на 5
- 17. Теоретический подход к подобному построению системы
- 18. Приемы запоминания таблицы умноженияПрием счета двойками, тройками,
- 19. Приемы запоминания таблицы умножения2. Прием последовательного сложения
- 20. Приемы запоминания таблицы умножения3. Прием прибавления слагаемого
- 21. Приемы запоминания таблицы умножения4. Прием взаимосвязанной пары:
- 22. Приемы запоминания таблицы умножения5. Прием запоминания последовательности
- 23. Приемы запоминания таблицы умножения6. Прием «порции» Для заучивания
- 24. Приемы запоминания таблицы умножения7. Прием запоминающегося случая
- 25. Приемы запоминания таблицы умножения8. Прием внешней опоры.В
- 26. Приемы запоминания таблицы умножения9. Прием запоминания таблицы
- 27. Приемы запоминания таблицы умножения10. Пальцевый счет при
- 28. Приемы запоминания таблицы умножения11. Мнемонические приемы при
- 29. Спасибо за внимание!
Слайд 2Смысл действия умножения
Действие умножения рассматривается как суммирование одинаковых слагаемых.
По
a • b = a + a + a + a + a…+ a , при b › 1
a • 1 = a, при b = 1
a • 0 = 0, при b = 0
Использование символики умножения позволяет сократить запись сложения одинаковых слагаемых. Запись вида 2 • 4 = 8 подразумевает сокращение записи вида 2 + 2 + 2 + 2 = 8. Её читают так : «по 2 взять 4 раза, получится 8»; или: «2 умножить на 4 получится 8»
Слайд 3Прежде, чем знакомиться с символикой записи действий и вычислениями результатов действий,
Слайд 4Виды заданий, которые предлагаются детям до знакомства с символикой умножения (в
Посчитай двойками (тройками, пятерками)
Нарисуй рисунок : «На трех тарелках по 2 апельсина». Сосчитай, сколько всего апельсинов.
Найди лишнюю запись:
2+2
2+2+2
2+2+2+2
2+3+2+2+2
Найди значение каждого выражения наиболее удобным способом.
Сделай запись выражения по рисунку:
Слайд 5
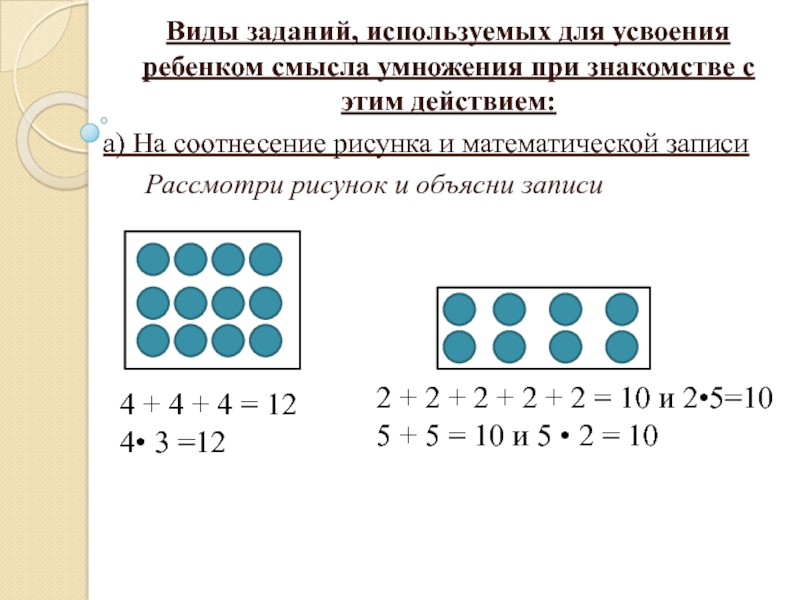
Виды заданий, используемых для усвоения ребенком смысла умножения при знакомстве
а) На соотнесение рисунка и математической записи
Рассмотри рисунок и объясни записи
4 + 4 + 4 = 12
4• 3 =12
2 + 2 + 2 + 2 + 2 = 10 и 2•5=10
5 + 5 = 10 и 5 • 2 = 10
Слайд 6
Виды заданий, используемых для усвоения ребенком смысла умножения при знакомстве
б) На нахождение суммы одинаковых слагаемых:
Рассмотри рисунки и закончи записи:
6 + 6 + 6 = …
6 • 3 = …
Слайд 7
Виды заданий, используемых для усвоения ребенком смысла умножения при знакомстве
в) На замену сложения умножением:
Замени, где возможно сложение умножением и вычисли результаты:
5 + 5 + 5 + 5 1 + 1 + 1 + 1 + 1 5 + 6 + 3
42 + 42 0 + 0 + 0 + 0 + 0 4 + 6 + 8
г) На понимание смысла определения действия умножения:
Рассмотри записи и объясни, какое число берется слагаемым и сколько раз берется слагаемым это число:
6 • 4 = 24 9 • 3 = …
6 + 6 + 6 + 6 = 24 9 + 9 + 9 = …
Слайд 8Выражение вида 3 • 5 называют произведением. Числа 3 и 5
Слайд 9
Среди данных выражений найдите такие, в которых первый
2 • 2 7 •3 6 • 2 1 • 6 3 • 5 3 • 2 7 • 3 3 • 4 3 • 1
Составьте произведение, в котором второй множитель равен 5. Найдите его значение.
Выберите примеры, в которых произведение равно 6. Подчеркните их красным цветом. Выберите примеры, в которых произведение равно 12. Подчеркните их синим цветом.
7 • 3 6 • 1 2 • 2 2 • 3 6 • 2 3 • 2 2 • 6
Как называют число 4 в выражении 5 • 4 ? Как называют число 5? Найдите произведение. Составьте пример, в котором произведение равно тому же числу, а множители другие.
Множители 8 и 2. Найдите произведение.
Задания, требующие распознавания компонентов действий и употребления их названий в речи:
Слайд 10 Если произведение разделить на один множитель, то получится другой множитель.
В
Например:
Решите уравнение 6 • х = 24. ( В уравнении неизвестен множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель х = 24 : 6, х = 4.)
Слайд 11Правило проверки действия умножения:
Произведение делят на множитель.
Сравнивают полученный результат с
Например: 18 • 4 = 72.
Проверка: 1) 72 : 4 = 18;
2) 18 = 18.
Слайд 12Табличное умножение
Изучение таблицы умножения является центральной задачей обучения во 2
Первые приемы составления таблиц умножения связаны со смыслом действия умножения. Результаты этих таблиц получают последовательным сложением одинаковых слагаемых.
Например:
Умножение числа на 2
Вычисли и запомни:
2+2 2 • 2
2+2+2 2 • 3
2+2+2+2 2 • 4
2+2+2+2+2 2 • 5
Расположенный рядом рисунок помогает ребенку получить результат пересчетом фигурок.
Слайд 13 При значении второго множителя больше 5 для получения результатов табличных значений
Например:
Вычисли и запомни:
2 • 6 = 2 • 5 + 2 = …
2 • 7 = 2 • 6 + 2 = …
2 • 8 = 2 • 7 + 2 = …
2 • 9 = 2 • 8 + 2 = …
В учебнике математики для 2 класса этот прием дан более пространно, и поэтому не всегда правильно понимается с точки зрения техники выполнения:
2+2+2+2+2+2 2 • 6
2+2+2+2+2+2+2 2 • 7 и т.п.
Слайд 14Прием перестановки множителей
Этот прием фактически является первым математическим законом относительно
От перестановки множителей произведение не меняется.
Например: 2 • 3 = 6
3 • 2 = 6
На основе этого правила, используемого как прием счета, составляется таблица умножения на 2 и на 3.
Слайд 15
Составление двух первых таблиц распределяется на два урока, что соответственно
На самом деле, многие дети учат каждую таблицу отдельно, поскольку недостаточный уровень развития гибкости мышления не позволяет им легко перестроить модель заученной схемы табличного случая в обратном порядке.
Слайд 16
При составлении таблицы умножения на 5 в 3классе, только первое
5 • 5 = 5+5+5+5+5 = 25.
Остальные случаи получают приемом прибавления пяти в предыдущему результату:
5 • 6 = 5 • 5 + 5 = 30
5 • 7 = 5 • 6 + 5 = 35
5 • 8 = 5 • 7 + 5 = 40
5 • 9 = 5 • 8 + 5 = 45
Одновременно с этой таблице составляется и взаимосвязанная с ней таблица умножения на 5: 6 • 5; 7 • 5; 8 • 5; 9 • 5.
Слайд 17
Теоретический подход к подобному построению системы изучения табличного умножения предполагает,
Слайд 18Приемы запоминания таблицы умножения
Прием счета двойками, тройками, пятерками
Данный прием применяется
Слайд 19Приемы запоминания таблицы умножения
2. Прием последовательного сложения
Данный прием связан со
Например: 6 • 7 = 6+6+6+6+6+6+6. Найти значение произведения чисел 6 и 7 таким способом достаточно сложно. Но для случаев
8 • 3 или 9 • 2 этот способ достаточно удобен.
Слайд 20Приемы запоминания таблицы умножения
3. Прием прибавления слагаемого к предыдущему результату (
Данный прием является вторым основным приемом получения результатов табличного умножения. Используется в том случае, если ребенок смог выучить хотя бы нексколько случаев из каждой таблицы. Это могут быть 3 – 4 певрых самых легких случая, или 2 – 3 наиболее запоминающихся случая.
Слайд 21Приемы запоминания таблицы умножения
4. Прием взаимосвязанной пары:
2 • 6 6
При хорошем понимании правила перестановки множителей ребенок заучивает в два раза меньше случаев табличного умножения, чем содержит полная таблица. Используя перестановку множителей, все остальные случаи можно получить из имеющихся.
Слайд 22Приемы запоминания таблицы умножения
5. Прием запоминания последовательности случаев с ориентиром на
Табличные случаи предлагаются ребенку на уроке «серией»:
3 • 2 3 • 3 3 • 4 3 • 5
Эту же «серию» учитель предлагает детям для заучивания к следующему уроку. На следующем уроке изучается новая «серия»:
3 • 6 3 • 7 3 • 8 3 • 9
Слайд 23Приемы запоминания таблицы умножения
6. Прием «порции»
Для заучивания ребенку предлагается «порция», состоящая
Слайд 24Приемы запоминания таблицы умножения
7. Прием запоминающегося случая в качестве опорного
Например, 5
Слайд 25Приемы запоминания таблицы умножения
8. Прием внешней опоры.
В качестве опоры используется рисунок
4 • 5 = 20