- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Ученический проект Координаты: что, зачем и почему?
Содержание
- 1. Ученический проект Координаты: что, зачем и почему?
- 2.
- 3. Типология проекта: практико-ориентированный, интегрированный, индивидуально- групповой, краткосрочный.Предметные области: математика, история, рисование, география.
- 4. Проблема: как лучше усвоить понятие “положительные и отрицательные числа” и выполнение действий с ними?
- 5. Цель проекта: научиться находить координаты точек и строить точки по заданным координатам.Участники проекта: учащиеся 6 класса.
- 6. Вопросы, направляющие проект: Основополагающий вопрос: Почему на
- 7. Ключевые слова:Координаты,
- 8. Слайд 8
- 9. Проект ученический «Координаты: что, зачем и почему?» Группа «Теоретики»Учащиеся 6 классаВиноградова Евгения,Чайникова Екатерина,Тимошенко Екатерина
- 10. Наши цели -Изучить теоретический и практический материал,
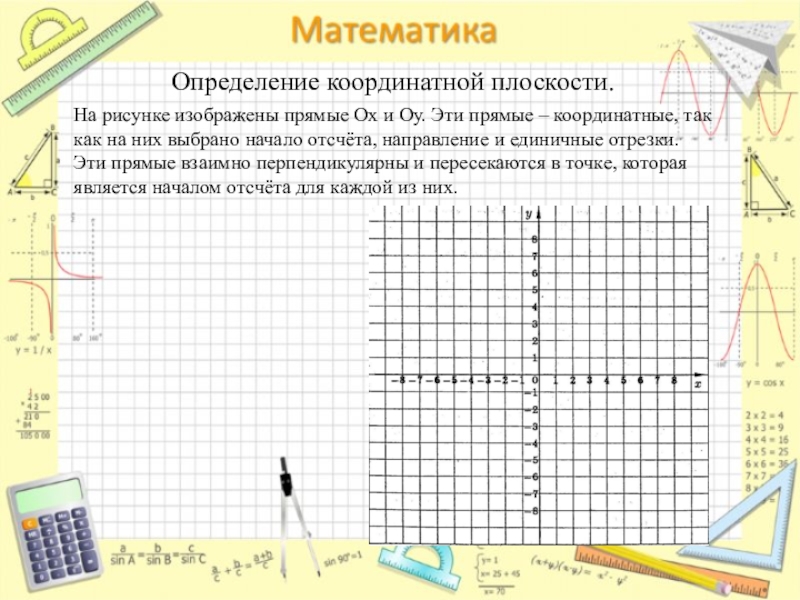
- 11. Определение координатной плоскости. На рисунке изображены
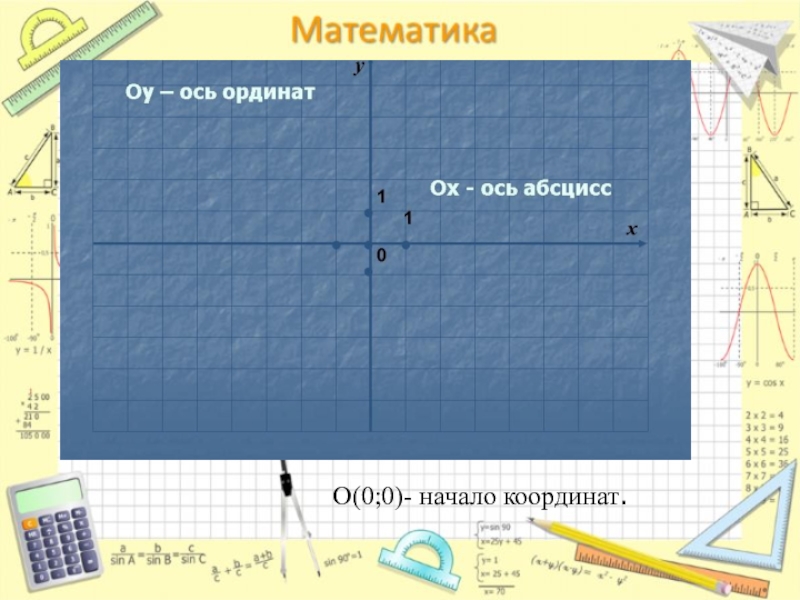
- 12. О(0;0)- начало координат.
- 13. Вопросы Можно ли утверждать, что на рисунке
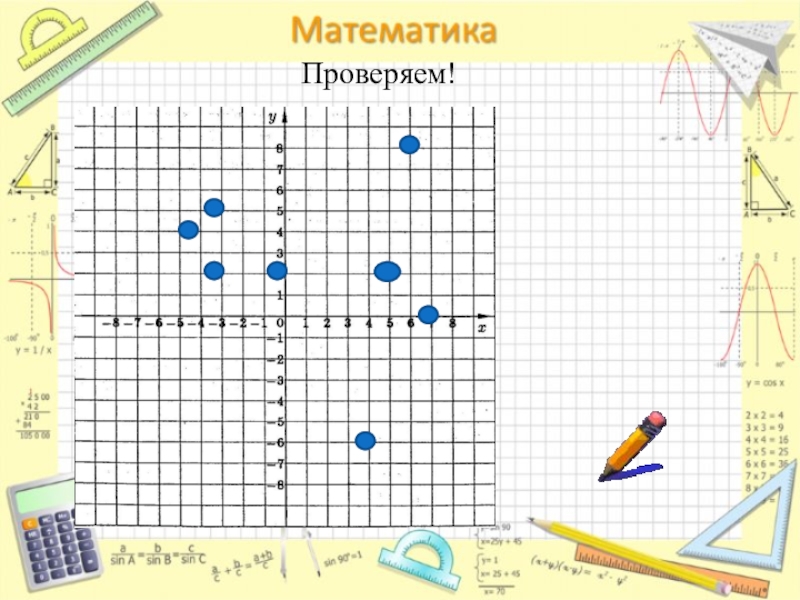
- 14. Задания:(5;2),(6;8),(-3;2),(4;-6),(-3;5),(-4;4),(0;2),(7;0)Постройте точки с заданными координатами:
- 15. Проверяем!
- 16. За единичный отрезок возьмите одну клетку.Постройте точки
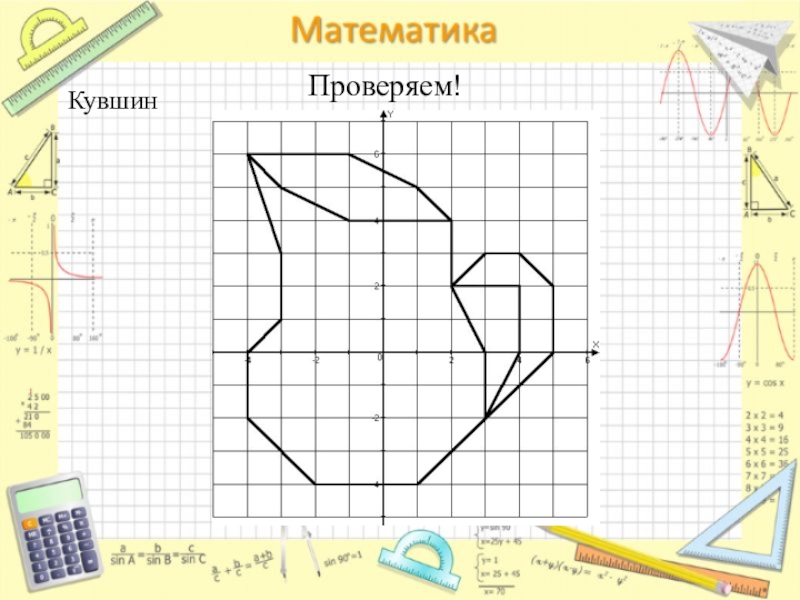
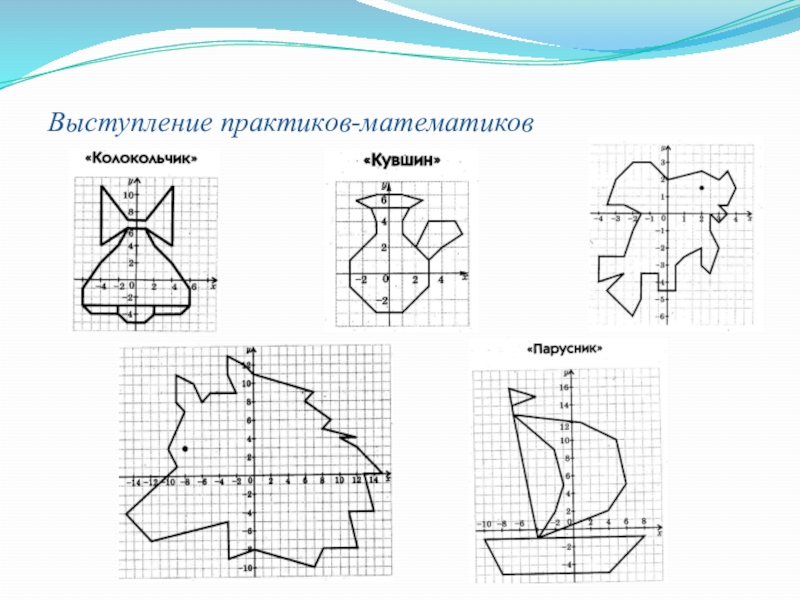
- 17. Проверяем!Кувшин
- 18. Слайд 18
- 19. Слайд 19
- 20. ВыводИзучив теоретический и практический материал, используя учебник,
- 21. Выступление группы историковГиппархПтолемейРене Декарт
- 22. Проект ученический «Координаты: что,
- 23. Цель проекта1. Изучить историю возникновения координат, первые
- 24. История возникновения координат на плоскости
- 25. Рене Декарт Основная заслуга в создании современного
- 26. Рене Декарт. Родился Декарт 31
- 27. Где в жизни встречается координатная плоскость?
- 28. Географические координатыНа карте каждая точка имеет две координаты: широту и долготу.
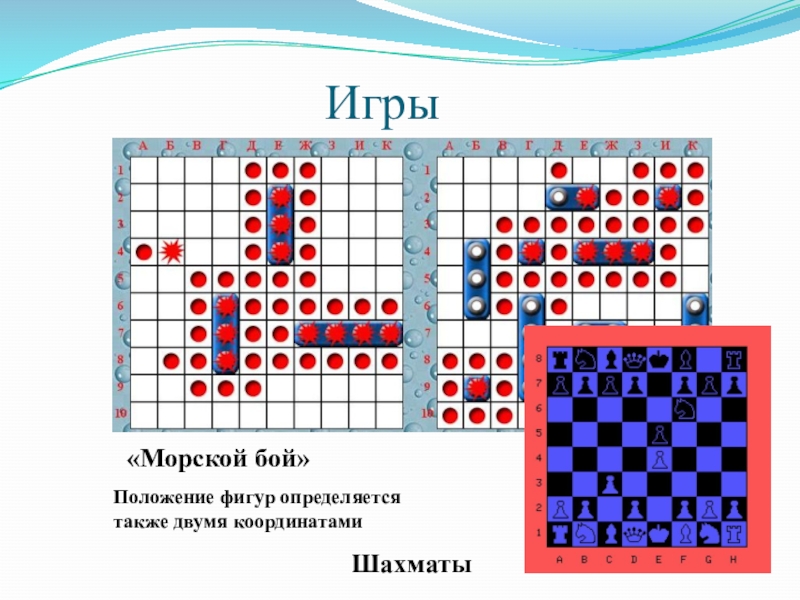
- 29. Игры«Морской бой»Положение фигур определяется также двумя координатамиШахматы
- 30. Координаты встречаются и в жизни. В билете
- 31. Вывод:Координатная плоскость окружает нас везде и на пути всей жизни.
- 32. Желаем удачи!!!Литературные источники:http://vm.ru/news/2014/02/10/genij-epohi-prosveshcheniya-5-interesnih-faktov-iz-biografii-rene-dekarta-234758.html
- 33. Выступление практиков-астрономов
- 34. Слайд 34
- 35. Цель: создать альбом звездного неба в
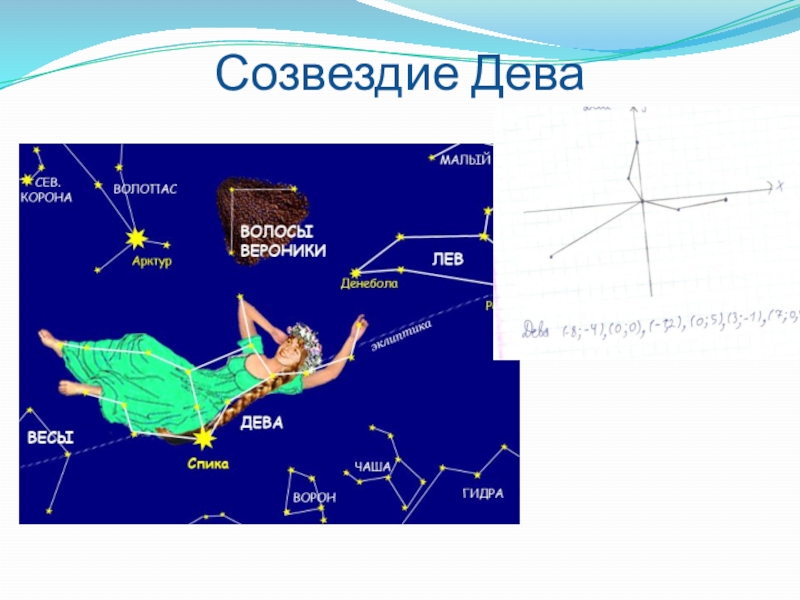
- 36. Созвездие Дева
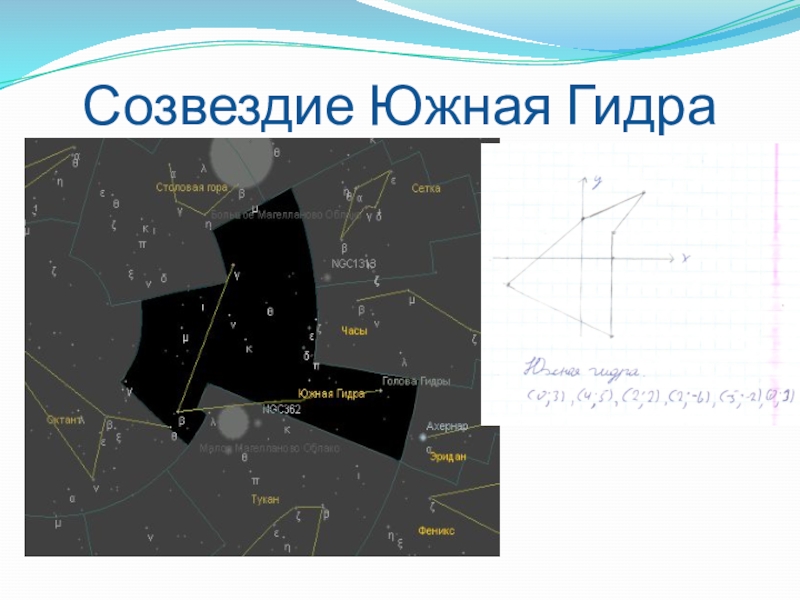
- 37. Созвездие Южная Гидра
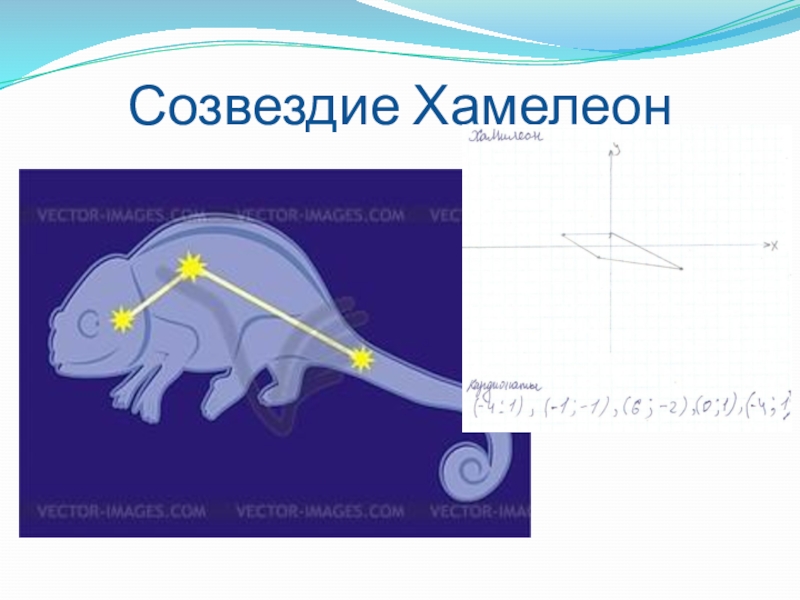
- 38. Созвездие Хамелеон
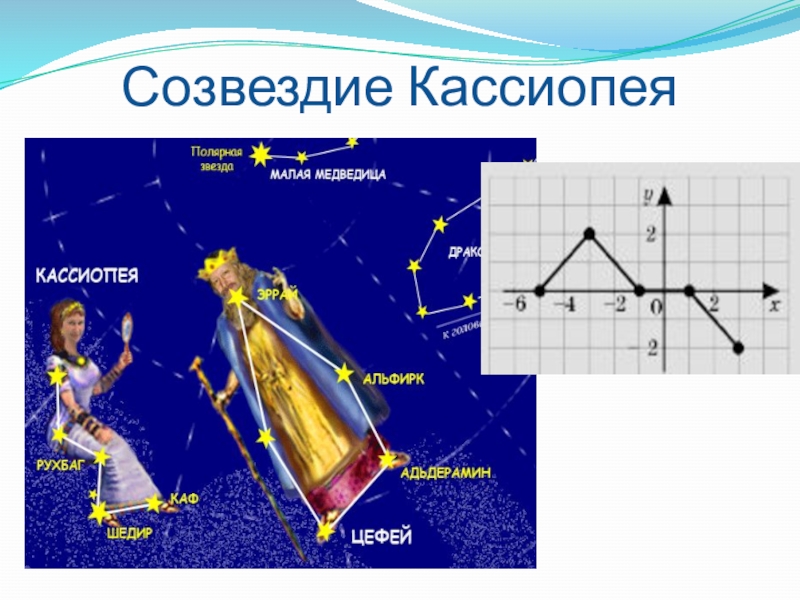
- 39. Созвездие Кассиопея
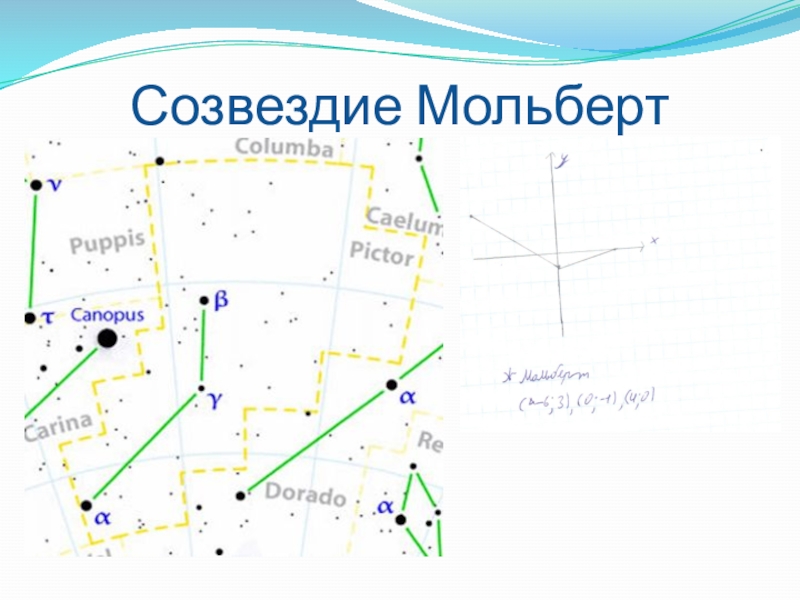
- 40. Созвездие Мольберт
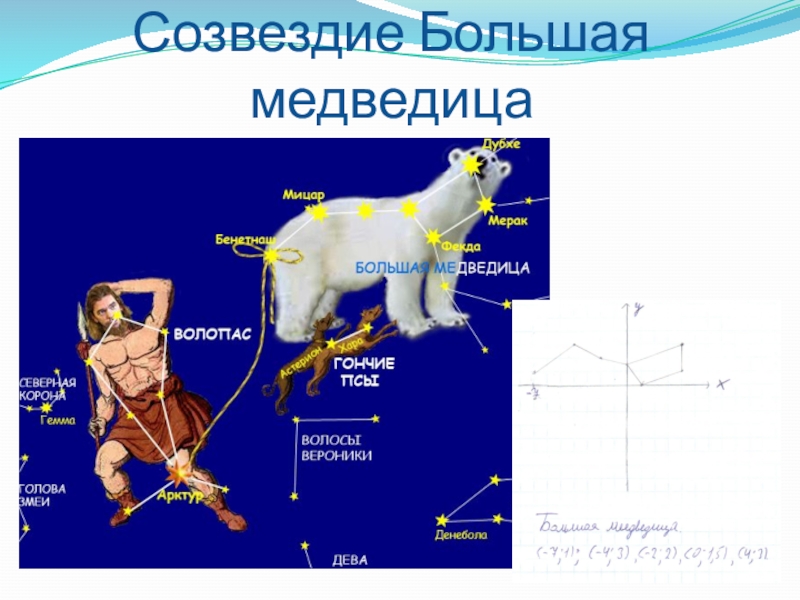
- 41. Созвездие Большая медведица
- 42. Выступление практиков-математиков
- 43. «Мир вокруг нас»Альбом «практиков-математиков»Выполнили учащиеся 6 класса Седенин Дмитрий, Погодин Александр, Кривоногов Иван
- 44. Создать альбом «Мир вокруг нас»Задачи:Выполнить рисунки
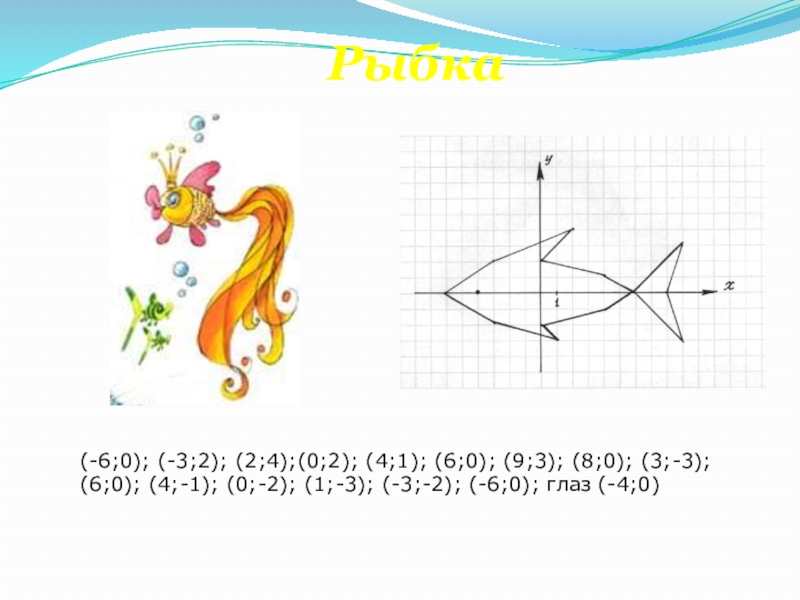
- 45. Рыбка(-6;0); (-3;2); (2;4);(0;2); (4;1); (6;0); (9;3); (8;0); (3;-3); (6;0); (4;-1); (0;-2); (1;-3); (-3;-2); (-6;0); глаз (-4;0)
- 46. Кот(-5;12); (-7;9); (-8;12); (-5;12); (-3;12); (0;12); (-1;9);
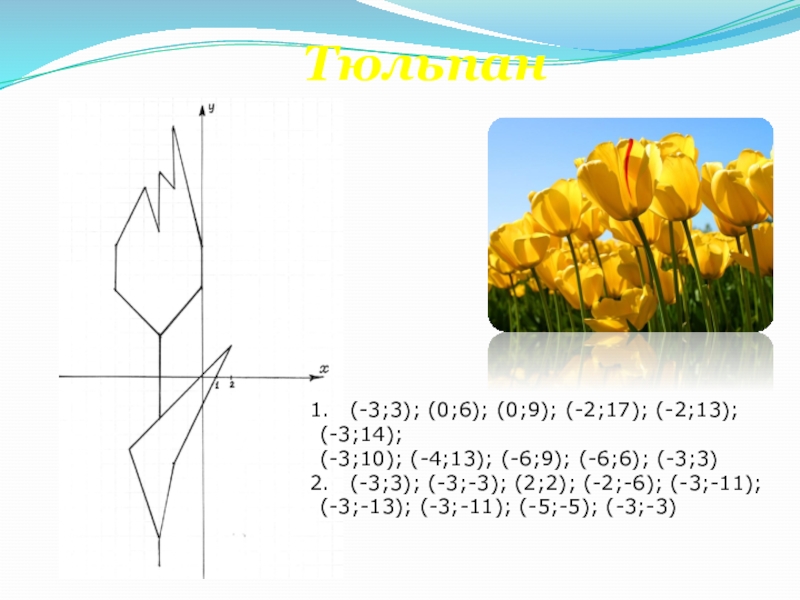
- 47. Тюльпан(-3;3); (0;6); (0;9); (-2;17); (-2;13); (-3;14);(-3;10); (-4;13);
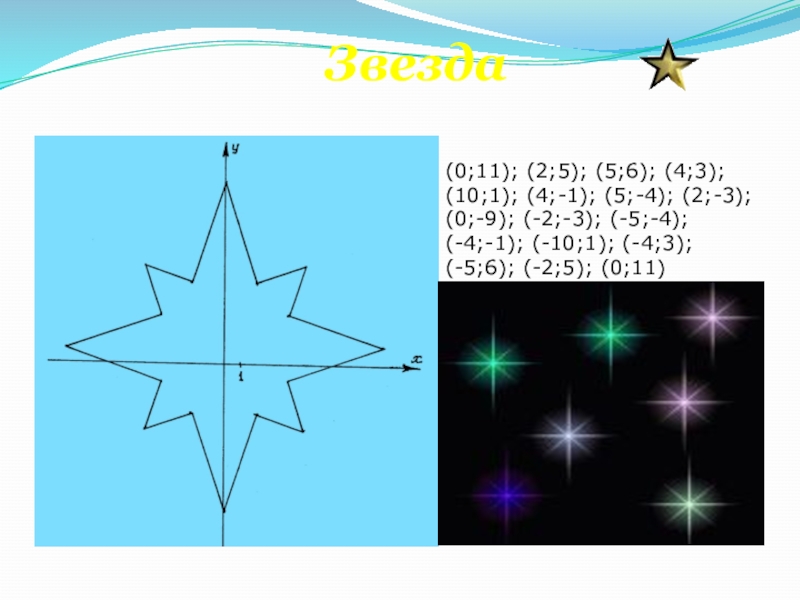
- 48. Звезда(0;11); (2;5); (5;6); (4;3); (10;1); (4;-1); (5;-4); (2;-3); (0;-9); (-2;-3); (-5;-4);(-4;-1); (-10;1); (-4;3);(-5;6); (-2;5); (0;11)
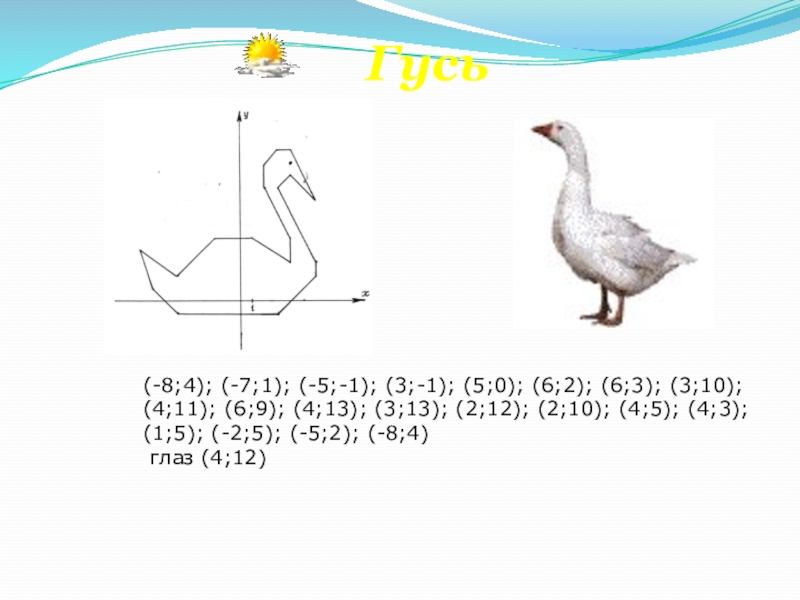
- 49. Гусь(-8;4); (-7;1); (-5;-1); (3;-1);
- 50. Ёлочка(0;14); (2;11); (1;11); (3;9); (1;9); (4; 6);
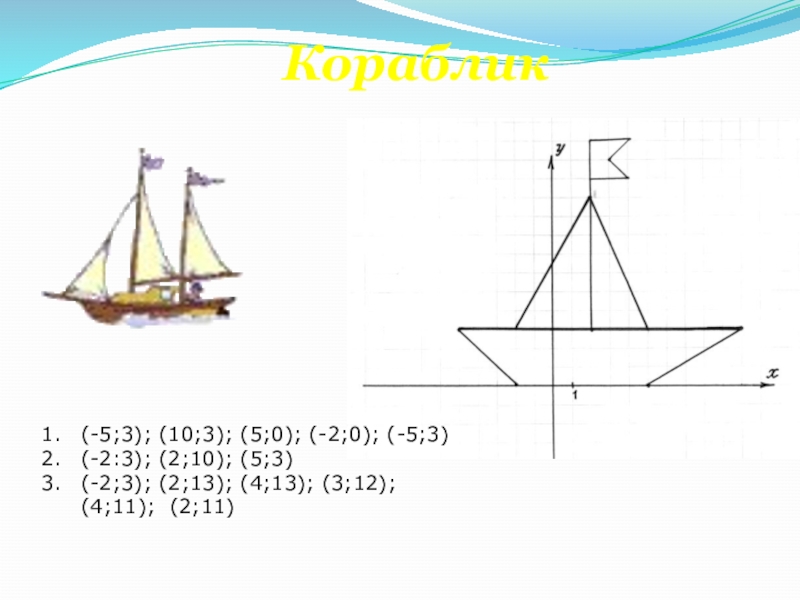
- 51. Кораблик(-5;3); (10;3); (5;0); (-2;0); (-5;3)(-2:3); (2;10); (5;3)(-2;3); (2;13); (4;13); (3;12); (4;11); (2;11)
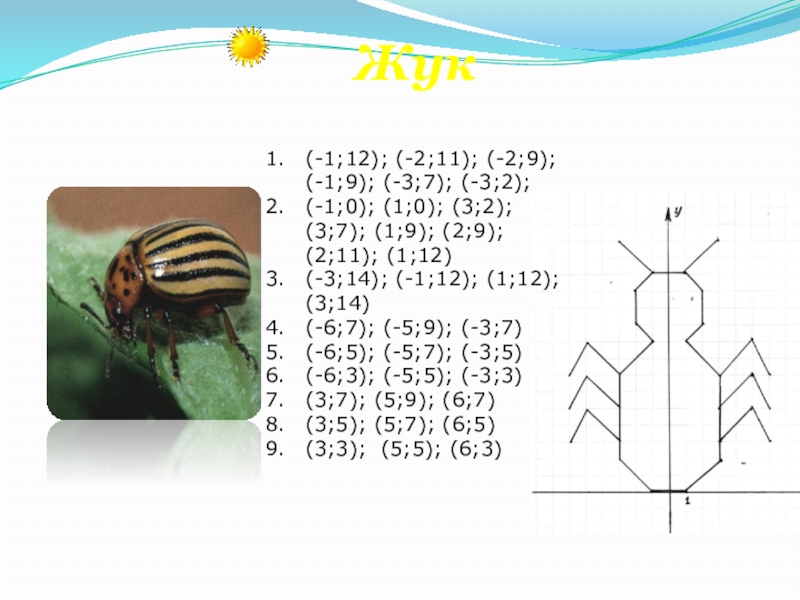
- 52. Жук(-1;12); (-2;11); (-2;9); (-1;9); (-3;7); (-3;2); (-1;0);
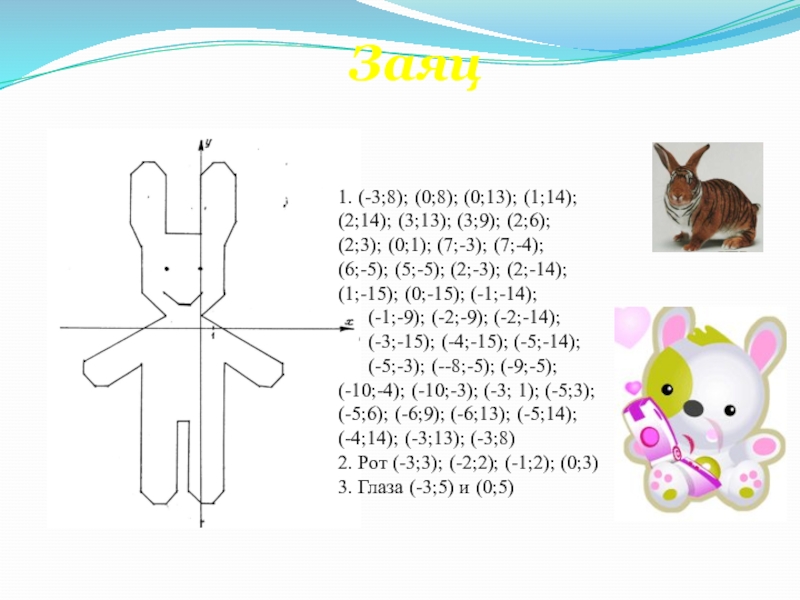
- 53. Заяц1. (-3;8); (0;8); (0;13); (1;14);(2;14); (3;13); (3;9);
- 54. Вывод Изучив теоретический и практический материал,
Слайд 2
Тема проекта: Положительные и отрицательные числа.
Вид проекта: Урочная деятельность.
Эпиграф : ««Жить на плоскости не скучно, веселей, чем на прямой…»
Слайд 3Типология проекта: практико-ориентированный,
интегрированный, индивидуально- групповой,
краткосрочный.
Предметные области: математика, история, рисование,
Слайд 4Проблема: как лучше усвоить понятие “положительные и отрицательные числа” и выполнение
Слайд 5Цель проекта: научиться находить координаты точек
и строить точки по заданным
Участники проекта: учащиеся 6 класса.
Слайд 6Вопросы, направляющие проект:
Основополагающий вопрос: Почему на уроках русского языка
мы
тетрадью в клетку?
Проблемный вопрос: Где можно применить положительные и
отрицательные числа?
Учебные вопросы:
Как отметить положительные и отрицательные числа
на координатной плоскости?
Как найти координаты точки в системе координат?
Как построить точку по заданным координатам?
Слайд 7
Ключевые слова:
Координаты, координатная плоскость, прямоугольная
система координат,
Клавдий Птолемей, геометрия, астрономия, география.
Слайд 8
Все в этой жизни
Дом чей-то, офис, цветы и грибы,
Место в театре, в классе свой стол
Если знать координатный закон.
Слайд 9
Проект ученический
«Координаты: что, зачем и почему?»
Группа «Теоретики»
Учащиеся 6 класса
Виноградова Евгения,
Чайникова
Тимошенко Екатерина
Слайд 10Наши цели
-Изучить теоретический и практический материал, используя книги, интернет и
-Изложить необходимый материал в презентации MS Power Point (наглядно, содержательно, красочно).
Слайд 11 Определение координатной плоскости.
На рисунке изображены прямые Ох и
как на них выбрано начало отсчёта, направление и единичные отрезки.
Эти прямые взаимно перпендикулярны и пересекаются в точке, которая
является началом отсчёта для каждой из них.
Слайд 13Вопросы
Можно ли утверждать, что на рисунке изображены координатные прямые?
(Можно)
(Под углом 90 градусов)
Слайд 14 Задания:
(5;2),(6;8),(-3;2),(4;-6),(-3;5),(-4;4),(0;2),(7;0)
Постройте точки с заданными координатами:
Слайд 16За единичный отрезок возьмите одну клетку.
Постройте точки с заданными координатами в
Что получилось?
Рисуем на координатной плоскости
Слайд 20Вывод
Изучив теоретический и практический материал, используя учебник, дополнительную литературу, интернет и
Зная координаты точки, мы можем её построить в координатной плоскости единственным образом.
И , наоборот, у построенной точки мы можем определить координаты.
Слайд 22
Проект ученический
«Координаты: что, зачем и почему?»
Группа «Историки»
Выполнили ученики 6
МОУ Ореховской СОШ
Смирнов Иван, Головач Александр и
Нечаев Михаил
Слайд 23Цель проекта
1. Изучить историю возникновения координат, первые применения.
2. Привести примеры применения
3. Сделать модель координатной плоскости.
Слайд 24История возникновения координат на плоскости
Древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции. Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами. Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Первоначальное применение координат связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.
Слайд 25Рене Декарт
Основная заслуга в создании
современного метода координат
принадлежит французскому
Рене Декарту. До наших времён дошла
такая история, которая подтолкнула
его к открытию. Занимая в театре места,
согласно купленным билетам, мы даже
не подозреваем, кто и когда предложил
ставший обычным в нашей жизни метод
нумерации кресел по рядам и местам.
Оказывается эта идея осенила
знаменитого философа, математика
и естествоиспытателя Рене Декарта
(1596-1650)– того самого, чьим именем
названы прямоугольные координаты.
Посещая парижские театры, он не уставал
удивляться путанице, перебранкам,
а подчас и вызовам на дуэль, вызываемыми
отсутствием элементарного порядка
распределения публики в зрительном зале.
Слайд 26Рене Декарт.
Родился Декарт 31 марта 1596 года в
в семье советника парламента Бретани Иоахима Декарта.
Мать Рене умерла от болезни легких, когда мальчику исполнился
всего один год. В 1606 году Рене отдали в коллеж Ла Флеш –
одно из лучших учебных заведений во Франции, основанное
иезуитами. Здесь он провёл девять лет, усваивая латынь,
древнегреческий, грамматику, риторику, богословие и
схоластику. После этого юноша окончил университет в Пуатье
и получил степень юриста, после чего поступил на военную
службу - сначала в революционной Голландии, затем в Германии.
Но и военным он не стал - возвратился в Париж и начал
активную научную деятельность.
Рене Декарт стал известен системой координат.
Как ученый внес большой вклад в математику, философию, физику.
Вместе с Ньютоном и Лейбницем основал современное исчисление.
Слайд 32Желаем удачи!!!
Литературные источники
:http://vm.ru/news/2014/02/10/genij-epohi-prosveshcheniya-5-interesnih-faktov-iz-biografii-rene-dekarta-234758.html
Слайд 34
Выполнила:
группа практиков-астрономов
Серов Кирилл, Алюев Никита, Дергачев Витя
Слайд 35Цель:
создать альбом звездного неба в координатах
Задачи:
Выполнить рисунки созвездий в координатах;
Найти
Отобразить материал в презентации.
Слайд 43«Мир вокруг нас»
Альбом
«практиков-
математиков»
Выполнили учащиеся 6 класса
Седенин Дмитрий,
Погодин Александр,
Кривоногов Иван
Слайд 44Создать альбом
«Мир вокруг нас»
Задачи:
Выполнить рисунки в координатах «Мир вокруг нас»;
Подобрать
Отобразить теоретический и практический материал в презентации.
Слайд 45Рыбка
(-6;0); (-3;2); (2;4);(0;2); (4;1); (6;0); (9;3); (8;0); (3;-3); (6;0); (4;-1); (0;-2);
Слайд 46Кот
(-5;12); (-7;9); (-8;12); (-5;12);
(-3;12); (0;12); (-1;9); (-3;12)
(-7;9); (-7;6); (-5;4); (-3;4);
(-5;4); (-7;3); (-8;1); (-8;8); (-6;9); (-5;-8); (-4;-9); (-3;-8); (-2;-9);
(0;-8); (0;1); (-1;3); (-3;4)
(-6;-9); (-2;9); (-3;-10); (-4;-10);
(-5;-11); (-5;-12); (-4;-13); (-2;-13); (3;-9); (3;-6); (2;-5); (1;-5); (0;-6)
(-10;8); (-5;6); (-4;6,5); (-3;6); (2;8)
(-11;6); (3;6)
(-10;5); (-5;6); (-3;6); (2;5)
Глаза (-5;8); (-5;7) и (-3;7); (-3;8)
Слайд 47Тюльпан
(-3;3); (0;6); (0;9); (-2;17); (-2;13);
(-3;14);
(-3;10); (-4;13); (-6;9); (-6;6); (-3;3)
(-3;3); (-3;-3);
(-3;-13); (-3;-11); (-5;-5); (-3;-3)
Слайд 48Звезда
(0;11); (2;5); (5;6); (4;3); (10;1); (4;-1); (5;-4); (2;-3); (0;-9); (-2;-3); (-5;-4);
(-4;-1);
(-5;6); (-2;5); (0;11)
Слайд 49 Гусь
(-8;4); (-7;1); (-5;-1); (3;-1); (5;0); (6;2); (6;3); (3;10);
глаз (4;12)
Слайд 50Ёлочка
(0;14); (2;11); (1;11); (3;9); (1;9); (4; 6); (2;6); (5;3); (1;3); (1;2);
(-1;9); (-3;9); (-1;11); (-2;11); (0;14)
Слайд 51Кораблик
(-5;3); (10;3); (5;0); (-2;0); (-5;3)
(-2:3); (2;10); (5;3)
(-2;3); (2;13); (4;13); (3;12); (4;11);
Слайд 52Жук
(-1;12); (-2;11); (-2;9); (-1;9); (-3;7); (-3;2);
(-1;0); (1;0); (3;2); (3;7); (1;9);
(-3;14); (-1;12); (1;12); (3;14)
(-6;7); (-5;9); (-3;7)
(-6;5); (-5;7); (-3;5)
(-6;3); (-5;5); (-3;3)
(3;7); (5;9); (6;7)
(3;5); (5;7); (6;5)
(3;3); (5;5); (6;3)
Слайд 53Заяц
1. (-3;8); (0;8); (0;13); (1;14);
(2;14); (3;13); (3;9); (2;6);
(2;3); (0;1); (7;-3); (7;-4);
(6;-5); (5;-5); (2;-3); (2;-14);
(1;-15); (0;-15); (-1;-14);
(-1;-9); (-2;-9); (-2;-14);
(-3;-15); (-4;-15); (-5;-14);
(-5;-3); (--8;-5); (-9;-5);
(-10;-4); (-10;-3); (-3; 1); (-5;3);
(-5;6); (-6;9); (-6;13); (-5;14);
(-4;14); (-3;13); (-3;8)
2. Рот (-3;3); (-2;2); (-1;2); (0;3)
3. Глаза (-3;5) и (0;5)
Слайд 54Вывод
Изучив теоретический и практический материал, используя учебник, дополнительную литературу,
Зная координаты точки, мы можем её построить в координатной плоскости единственным образом.
И , наоборот, у построенной точки мы можем определить координаты.