- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Учебный проект: Творческое исследование площадей многоугольников
Содержание
- 1. Учебный проект: Творческое исследование площадей многоугольников
- 2. Автор проекта: Хазина Наталья ПетровнаУчастники проекта : учащиеся 8 «Б» класса
- 3. Дидактические цели проекта:1.Расширить знания обучающихся о треугольниках,
- 4. Основными задачами проекта являютсяформирование у обучающихся понятия
- 5. Прогнозируемые результатыВ результате выполнения проекта «Творческое исследование
- 6. Прогнозируемые результатыВ результате выполнения проекта «Площади многоугольников»
- 7. Группа «Исследователи свойств многоугольников»Задачи:Изучить свойства треугольника, квадрата,
- 8. Группа «Исследователи площади треугольников»Задачи:1.Изучить доказательство площади треугольника.2.Найти
- 9. Группа «Исследователи площади квадрата» Задачи:1.Изучить доказательство площади
- 10. Группа «Исследователи площади прямоугольника» Задачи:1.Изучить доказательство площади
- 11. Группа «Исследователи площади трапеции»Задачи: 1.Изучить доказательство площади
- 12. Во время отчетов рабочих групп учитель, вместе
- 13. Отчётные материалы1.Создание презентации (слайды, рисунки)2. Подготовка сообщений.
- 14. В результате плодотворной работы групп представляем вашему вниманию наш отчет.
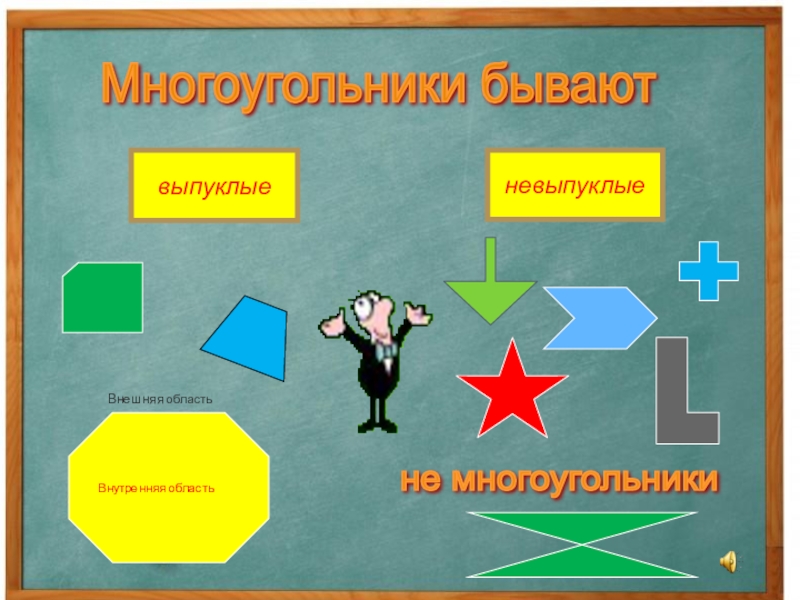
- 15. Внутренняя областьвыпуклыеневыпуклыеМногоугольники бывают Внешняя областьне многоугольники
- 16. Площадью называется величина, характеризующая размер геометрической фигуры.
- 17. Определение площадей геометрических фигур – одна из древнейших практических задач.
- 18. Правильный подход к их решению был найден
- 19. Когда каменщики определяют площадь прямоугольной стены дома они перемножают высоту и ширину стены.
- 20. Долгий был путь к нахождению формул, позволяющим найти площади любых фигур.
- 21. В настоящее время существуют и механические приборы для вычисления площадей плоских фигур – так называемые планиметры.
- 22. Любая плоская геометрическая фигура имеет площадь
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
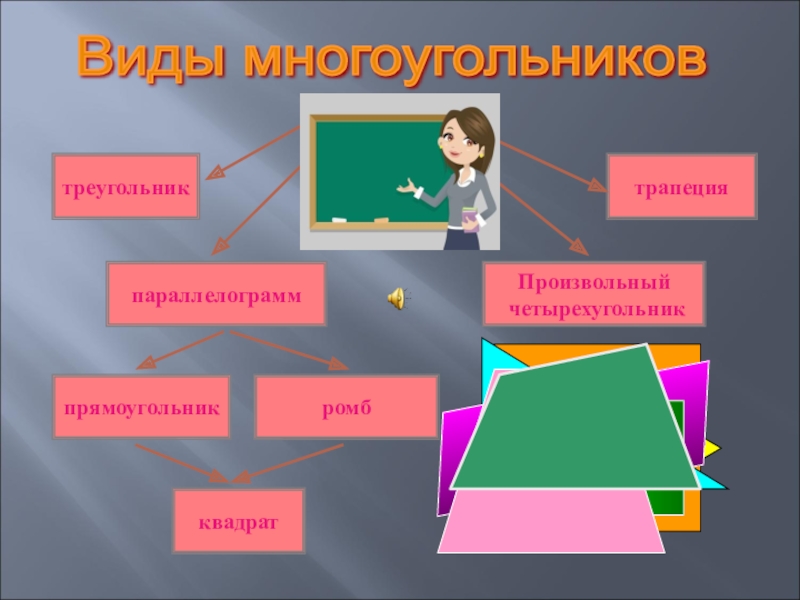
- 27. трапецияквадраттреугольникПроизвольный четырехугольникпараллелограммпрямоугольникромбВиды многоугольников
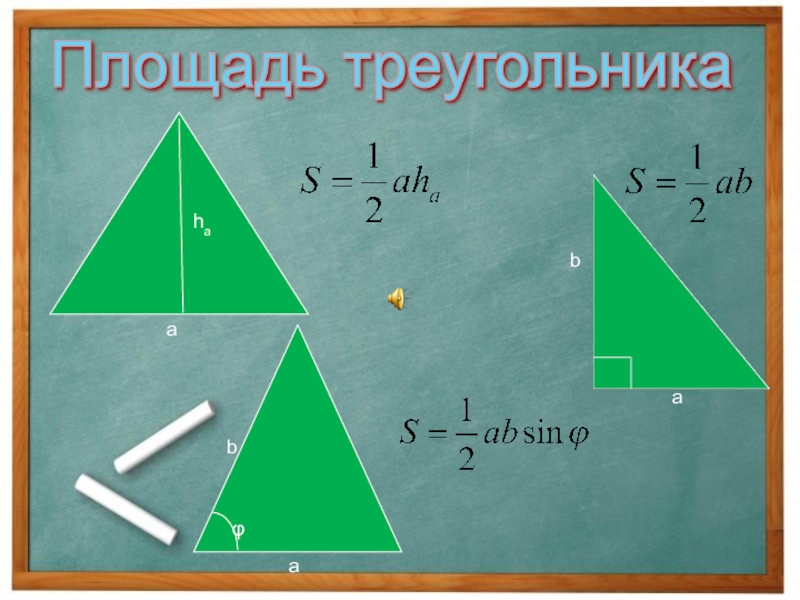
- 28. Площадь треугольника habaφaba
- 29. Медиана – это отрезок, соединяющий любую вершину треугольника с
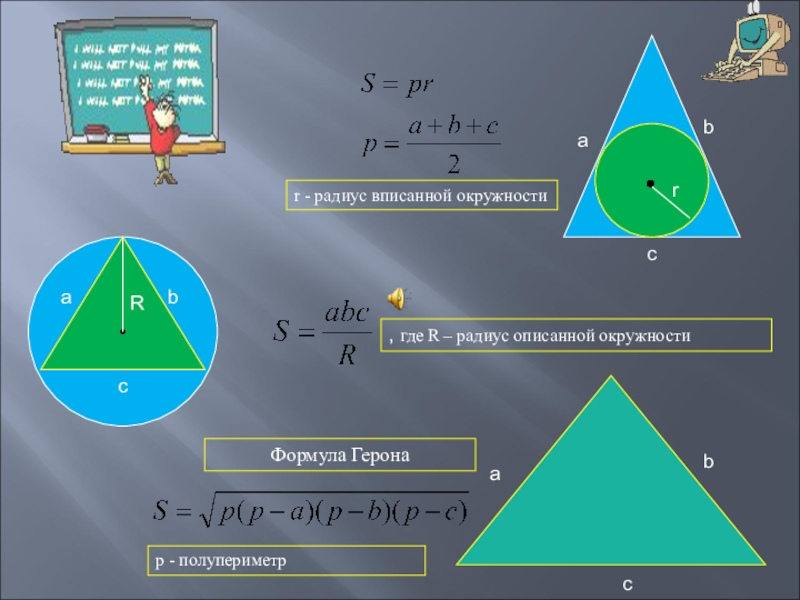
- 30. cbaacbracbRФормула Геронар - полупериметрr - радиус вписанной окружности, где R – радиус описанной окружности
- 31. Последнее выражение называется формулой Герона.Основная ее задача -
- 32. Площадь квадрата daaaНу, какой же он добряк!
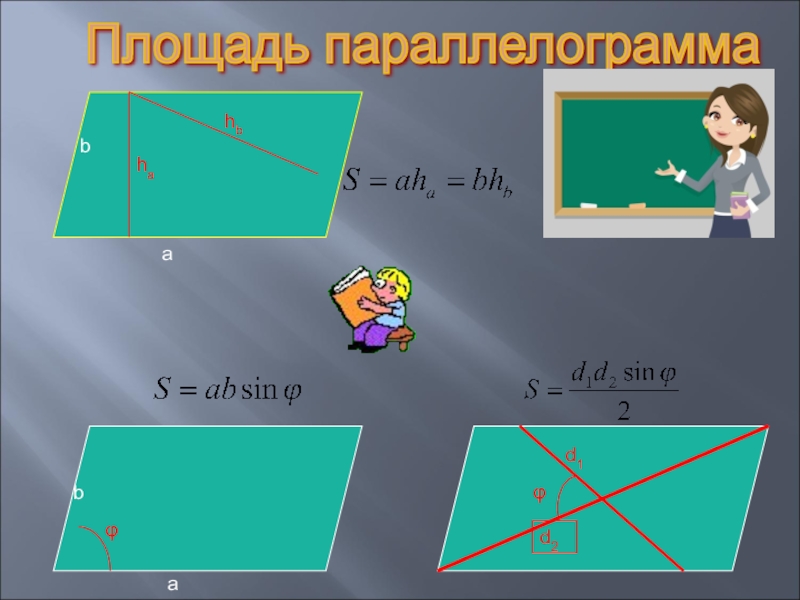
- 33. d1bhbbhaaaφd2φПлощадь параллелограмма
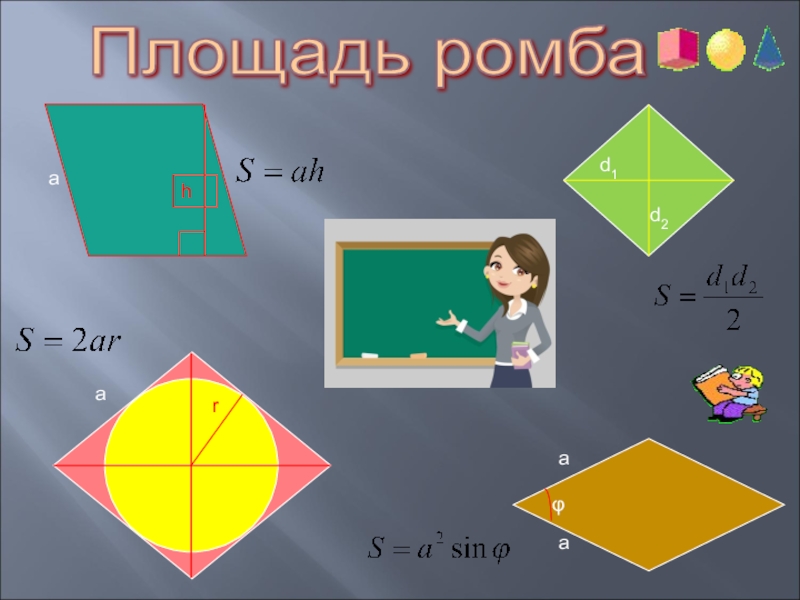
- 34. Площадь ромба aaφahrad1d2
- 35. Площадь прямоугольника φd2d1abbaЕго знает каждый школьник, Брат
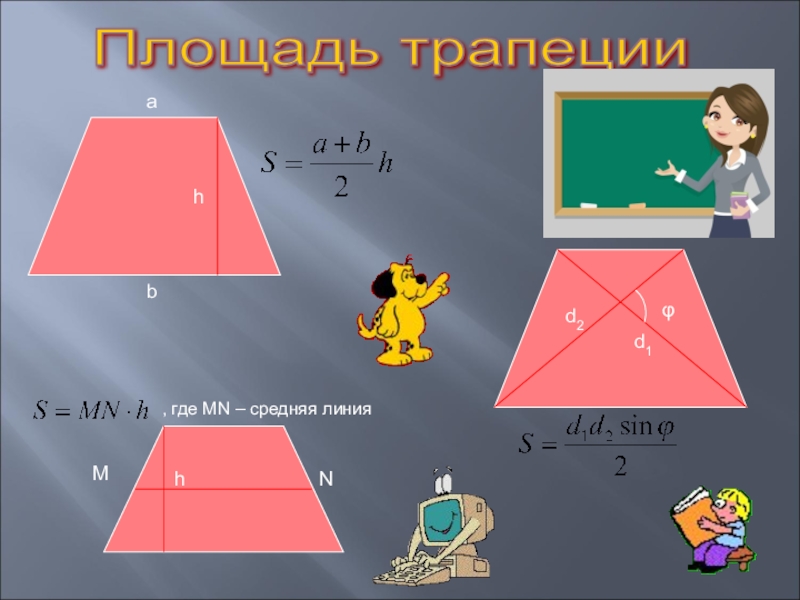
- 36. Площадь трапеции MhNhabd1d2φ, где MN – средняя линия
- 37. Площадь произвольного четырехугольника (для описанного четырехугольника)(для вписанного четырехугольника)
- 38. Историческое применение площадей многоугольниковГруппы в результате исследования
- 39. Египет.Если не учитывать весьма малый вклад древних
- 40. Греция.Около 600 года до н.э. ионийские греки,
- 41. История головоломки "Танграм"Головоломка "Танграм" - квадрат, разрезанный
- 42. Слайд 42
- 43. Практическое применение площадей многоугольников.Группы в результате исследования
- 44. Фантазия архитектора может достигнуть и таких форм и это придает зданию весьма оригинальный вид.
- 45. Слайд 45
- 46. Применение площадей в архитектуреРебята узнали, что строительное
- 47. Применение площадей в географииГруппы выяснили следующее, что в
- 48. Слайд 48
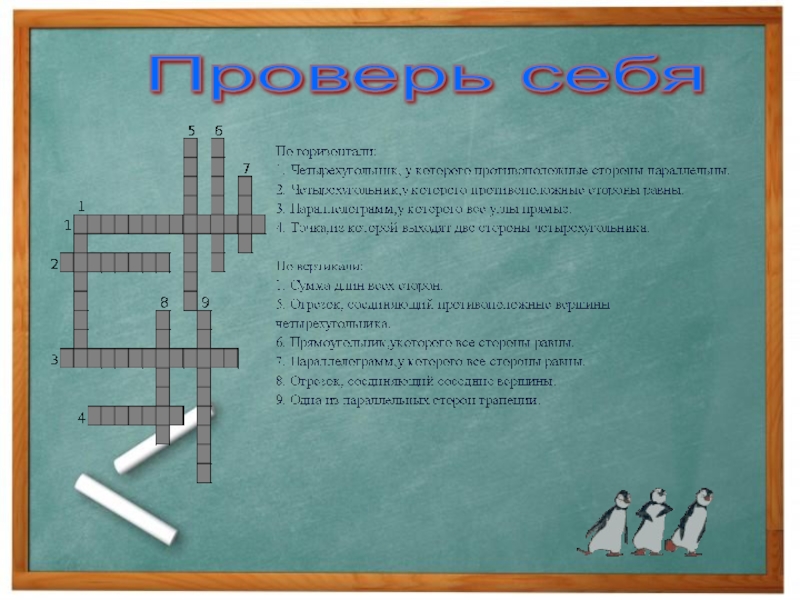
- 49. Проверь себя
- 50. . Проверь себя
- 51. . Проверь себя Ответ: 14
- 52. . Проверь себя Ответ: 24
- 53. . Проверь себя Ответ: 37
- 54. ВЫВОД.
- 55. Автор презентации учитель МАОУ СОШ№148 (филиал) Хазина
Слайд 3
Дидактические цели проекта:
1.Расширить знания обучающихся о треугольниках, квадратах, прямоугольниках и трапециях,
2.Развить творческую активность обучающихся, умение делать обобщения на основе данных, полученных в результате исследований.
3.Развить познавательную деятельность обучающихся, которая в свою очередь, способствует развитию разносторонней личности.
4. Воспитывать у обучающихся стремление к самосовершенствованию, удовлетворению познавательных потребностей.
Слайд 4
Основными задачами проекта являются
формирование у обучающихся понятия площади многоугольников;
развитие исследовательских навыков;
развитие
формирование навыков проектной работы.
Слайд 5
Прогнозируемые результаты
В результате выполнения проекта «Творческое исследование площадей многоугольников» обучающиеся должны:
знать
продемонстрировать осведомленность о практическом применении площадей этих фигур;
получать навыки анализа и систематизации полученных ранее знаний; навыки выполнения проектной работы;
самостоятельно работать с дополнительной литературой.
Слайд 6
Прогнозируемые результаты
В результате выполнения проекта «Площади многоугольников» обучающиеся должны:
знать определения треугольника,
продемонстрировать осведомленность о практическом применении площадей этих фигур;
знать сведения вычисления площадей в древности;
получать навыки анализа и систематизации полученных ранее знаний; навыки выполнения проектной работы;
самостоятельно работать с дополнительной литературой.
Слайд 7
Группа «Исследователи свойств многоугольников»
Задачи:
Изучить свойства треугольника, квадрата, прямоугольника и трапеции.
Найти определения
Сравнить современные трактовки с древними.
Составить кроссворд
Слайд 8
Группа «Исследователи площади треугольников»
Задачи:
1.Изучить доказательство площади треугольника.
2.Найти информацию о нахождении площадей
3.Найти материал, подтверждающий применение площадей в архитектуре и строительстве.
4.Найти материал, подтверждающий применение площадей в географии.
Слайд 9
Группа «Исследователи площади квадрата»
Задачи:
1.Изучить доказательство площади квадрата.
2.Найти информацию о нахождении
3.Найти материал, подтверждающий применение площадей в архитектуре и строительстве.
4.Найти материал, подтверждающий применение площадей в географии
Слайд 10
Группа «Исследователи площади прямоугольника»
Задачи:
1.Изучить доказательство площади прямоугольника.
2.Найти информацию о нахождении
3.Найти материал, подтверждающий применение площадей в архитектуре и строительстве.
4.Найти материал, подтверждающий применение площадей в географии.
Слайд 11
Группа «Исследователи площади трапеции»
Задачи:
1.Изучить доказательство площади трапеции .
2.Найти информацию о
3.Найти материал, подтверждающий применение площадей в архитектуре и строительстве.
4.Найти материал, подтверждающий применение площадей в географии.
Слайд 12
Во время отчетов рабочих групп учитель, вместе с жюри из обучающихся
Слайд 18
Правильный подход к их решению был найден не сразу. Древние греки
Слайд 19
Когда каменщики определяют площадь прямоугольной стены дома они перемножают высоту
Слайд 21
В настоящее время существуют и механические приборы для вычисления площадей плоских
Слайд 27трапеция
квадрат
треугольник
Произвольный
четырехугольник
параллелограмм
прямоугольник
ромб
Виды многоугольников
Слайд 29Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы
Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника ( AD, BE, CF, ) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).
Средняя линия треугольника – это отрезок, соединяющий средние точки боковых сторон треугольника. Средняя линия треугольника равна половине его основания и параллельна ему.
Слайд 30
c
b
a
a
c
b
r
a
c
b
R
Формула Герона
р - полупериметр
r - радиус вписанной окружности
, где R –
Слайд 31
Последнее выражение называется формулой Герона.
Основная ее задача - измерить площадь, т.е. найти
Слайд 32Площадь квадрата
d
a
a
a
Ну, какой же он добряк!
Всем он друг, а может
брат. А углы-то все прямые, Да и стороны родные. Хоть положь или поставь, Был квадрат и есть квадрат.
Слайд 35
Площадь прямоугольника
φ
d2
d1
a
b
b
a
Его знает каждый школьник,
Брат квадрата – прямоугольник.
Его используют везде:
И
Слайд 37Площадь произвольного четырехугольника
(для описанного четырехугольника)
(для вписанного четырехугольника)
Слайд 38
Историческое применение площадей многоугольников
Группы в результате исследования выяснили,
что возникновение геометрии
прежде всего, с развитием ремесел, культуры, искусств,
с трудовой деятельностью человека и наблюдением за окружающим миром.
Об этом свидетельствуют названия геометрических фигур.
Например, название фигуры «трапеция» происходит от греческого слова «трапезион» (столик),
от которого также произошло слово «трапеза» и другие родственные слова.
а термин «линия» возник от латинского «линиум» (льняная нить).
Одна из главных величин в геометрии - площадь.
Площадь - это величина, характеризующая размер той части плоскости,
которая заключена внутри плоской замкнутой фигуры. Обозначается буквой S.
Слайд 39
Египет.
Если не учитывать весьма малый вклад древних обитателей долины между Тигром
нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянам стали такие виды их деятельности, как возведение пирамид и изобразительное искусство. Египтяне при применении геометрических знаний всецело руководствовались интуицией и приближенными представлениями.
Слайд 40
Греция.
Около 600 года до н.э. ионийские греки, совершившие путешествие в Египет,
Фалес первым начал доказывать истинность геометрических соотношений, последовательно выводя их логически из некоторого набора метод дедуктивного
рассуждения, которому представало стать доминирующим в геометрии и фактически - во всей математике, сохраняя свое фундаментальное значение и в наши дни.
Слайд 41
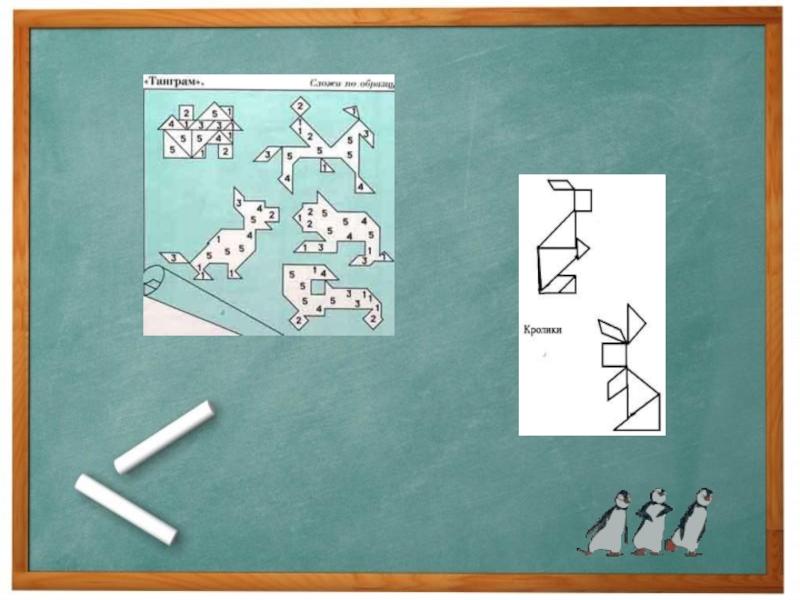
История головоломки "Танграм"
Головоломка "Танграм" - квадрат, разрезанный на 7 частей из
Слайд 43
Практическое применение площадей многоугольников.
Группы в результате исследования пришли к выводу, что
Слайд 44
Фантазия архитектора может достигнуть и таких форм и это придает зданию
Слайд 46
Применение площадей в архитектуре
Ребята узнали, что строительное производство сегодня — это
Непосредственно на строительном объекте столяр устанавливает оконные и дверные блоки, производит настилку дощатых и паркетных полов, монтирует встроенную мебель и т. д. Выполнение такой работы невозможно без знания устройства и правил эксплуатации деревообрабатывающих станков, знания технологии и организации строительного производства, умения читать чертежи. Профессия требует объемного воображения, хорошего глазомера, знания геометрии, рисования, черчения. Это лишь одна строительная профессия, а их очень много. Во всех случаях невозможно обойтись без знаний геометрии, без расчетов площадей поверхностей пола , стены , крыши.
Слайд 47
Применение площадей в географии
Группы выяснили следующее, что в геодезии- науке об определении
Геодезические работы ведутся на трех уровнях. Во-первых, это плановая съемка на местности – определение положения точек на земной поверхности относительно местных опорных пунктов для составления топографических карт, используемых, например, при строительстве плотин и дорог или составлении земельного кадастра. Следующий уровень включает проведение съемок в масштабах всей страны; при этом площадь и форма поверхности определяются по отношению к глобальной опорной сети с учетом кривизны земной поверхности.
Слайд 54 ВЫВОД. Во время подготовки к проекту каждой группе пришлось выполнять свою работу.
Слайд 55Автор презентации учитель МАОУ СОШ№148 (филиал) Хазина Наталья Петровна и обучающиеся 8
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ:
«Геометрия 7 - 9 класс». Авторы –Л.С. Атанасян и др.
«История математики в школе.VII- VIII классы».Автор- Г.И. Глейзер.
«Словарь-справочник по математике». Автор-Н.И. Александров , И.П. Ярандай.
«Математика в понятиях, определениях и терминах» Авторы- О. В. Мантуров и др.
Справочный материал по геометрии;(www.bymath.net)
Исторические сведения о происхождении математики; картинки (www.coolreferat.com)
Дидактический материал за курс 8 класса к учебнику Л.С.Атанасяна