- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Учебный проект по математике Теория игр
Содержание
- 1. Учебный проект по математике Теория игр
- 2. Игра — и вдруг математика? Оказывается, математики
- 3. Но только ли игры можно рассматривать
- 4. ТЕОРИЯ ИГРИГР ТЕОРИЯ, раздел математики, предметом которого
- 5. Классификация игрПо выигрышу игры можно разделить на
- 6. Следует особо подчеркнуть:Теория игр является очень сложной
- 7. крестики и нолики на языке теории игр
- 8. Рациональность игроков Представим себе идеального игрока, который
- 9. Игра в крестики и нолики монетами или
- 10. Игра «крестики-нолики» имеет древнее происхождение
- 11. Правила игры крестики-нолики Основные термины и
- 12. Играют два соперника: один чёрными фишками (камнями),
- 13. 60-е годы – игра «тико»Известно много разновидностей
- 14. Тик-Так-Тоу На первый взгляд кажется непонятным, что
- 15. Первый игрок (ему принадлежат крестики) может сделать
- 16. Дерево игровых ситуаций Дерево игровых
- 17. Слайд 17
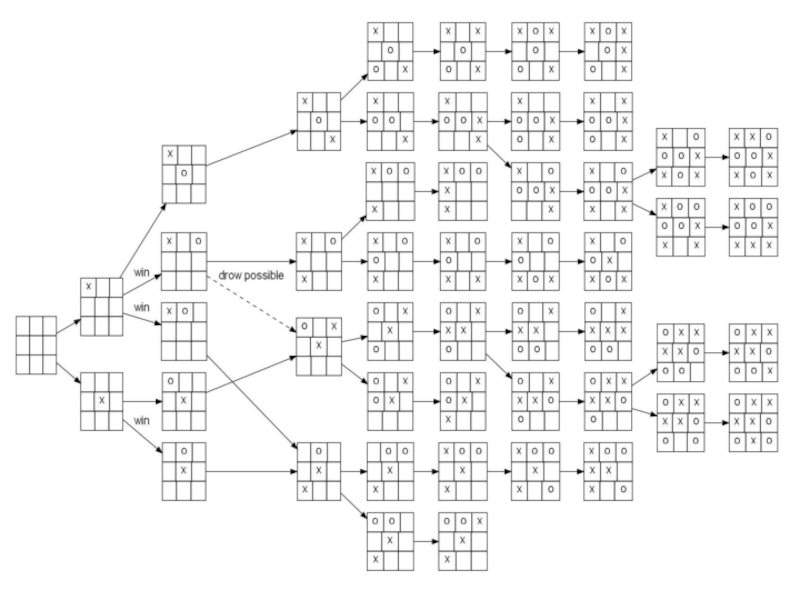
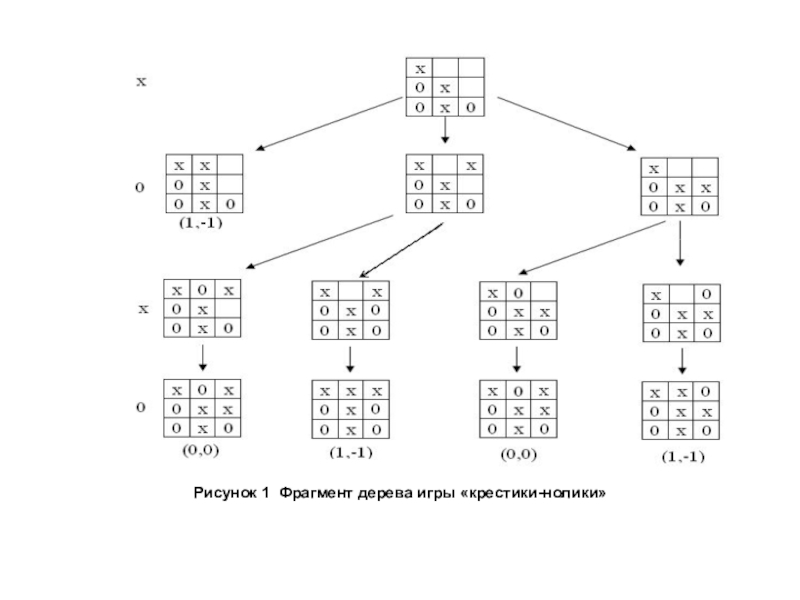
- 18. Фрагмент дерева игры «крестики-нолики»В начальной позиции фрагмента
- 19. Рисунок 1 Фрагмент дерева игры «крестики-нолики»
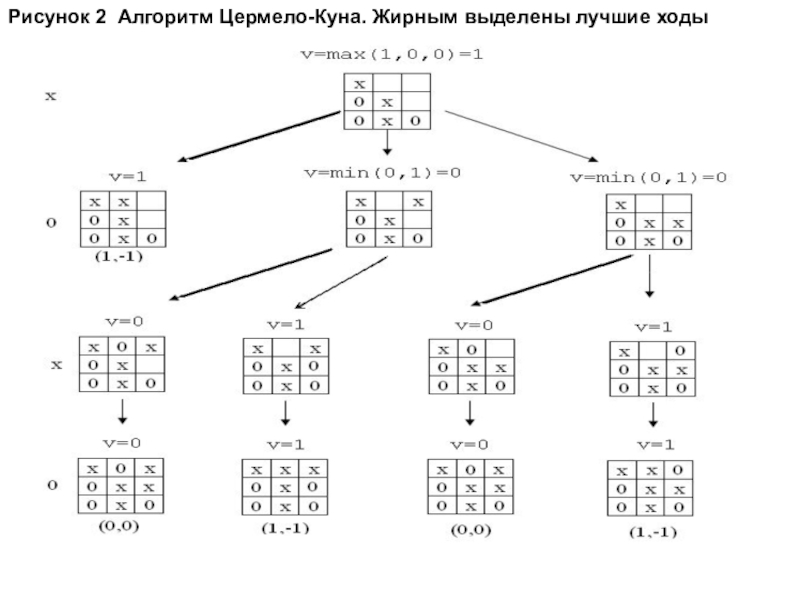
- 20. Алгоритм Цермело-Куна. В позиционных играх
- 21. Рисунок 2 Алгоритм Цермело-Куна. Жирным выделены лучшие ходы
- 22. Что такое выигрышная стратегия? Позиции, в которых
- 23. Задача Тема: Теория игр
- 24. Родственные игры5 в ряд. Играют на
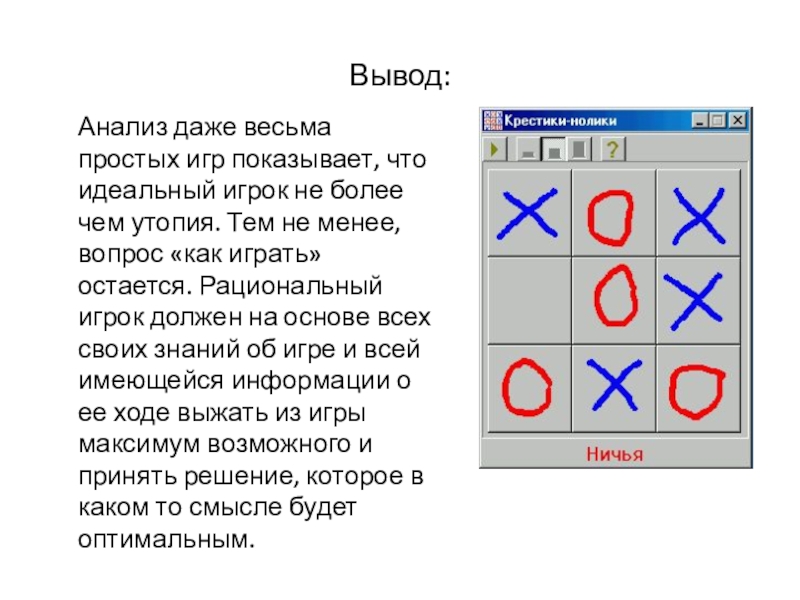
- 25. Вывод: Анализ даже весьма простых
- 26. ПРИЛОЖЕНИЕ: "Крестики-нолики 3D"
- 27. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 2Игра — и вдруг математика?
Оказывается, математики занимаются изучением закономерностей некоторых игр,
Теория игр (более подходящее название - теория конфликта, или теория конфликтных ситуаций) зародилась как теория рационального поведения двух игроков с противоположными интересами.
Слайд 3Но только ли игры можно рассматривать
с математической точки зрения?
Видимо, нигде и никому не обойтись без неё!
Везде математика приходит нам на помощь.
Слайд 4ТЕОРИЯ ИГР
ИГР ТЕОРИЯ, раздел математики, предметом которого является анализ принятия оптимальных
Слайд 5Классификация игр
По выигрышу игры можно разделить на игры с нулевой и
По полноте имеющейся информации – на игры с полной и неполной информацией.
По характеру получения информации — на игры в нормальной форме (игроки получают всю предназначенную им информацию до начала игры) и динамические игры (информация поступает игрокам в процессе развития игры).
По характеру информационного взаимодействия – игры с сообщениями или без оных. Сообщения могут содержать, например, предложения или угрозы.
По количеству стратегий — на конечные и бесконечные игры.
По количеству розыгрышей игры – на однократно разыгрываемые и повторяющееся игры.
Слайд 6Следует особо подчеркнуть:
Теория игр является очень сложной областью знания.
Теория игр прививает
Теория игр всегда имеет дело с особым типом мышления, стратегическим.
Человек, знакомый с теорией игр, реже считает других глупее себя, - и потому избегает многих непростительных ошибок.
Теория игр не рассчитана на то, чтобы придать решительности, настойчивости в достижении целей, невзирая на неопределенность и риск.
Знание основ теории игр не дает нам явного выигрыша, но оберегает нас от свершения глупых и ненужных ошибок.
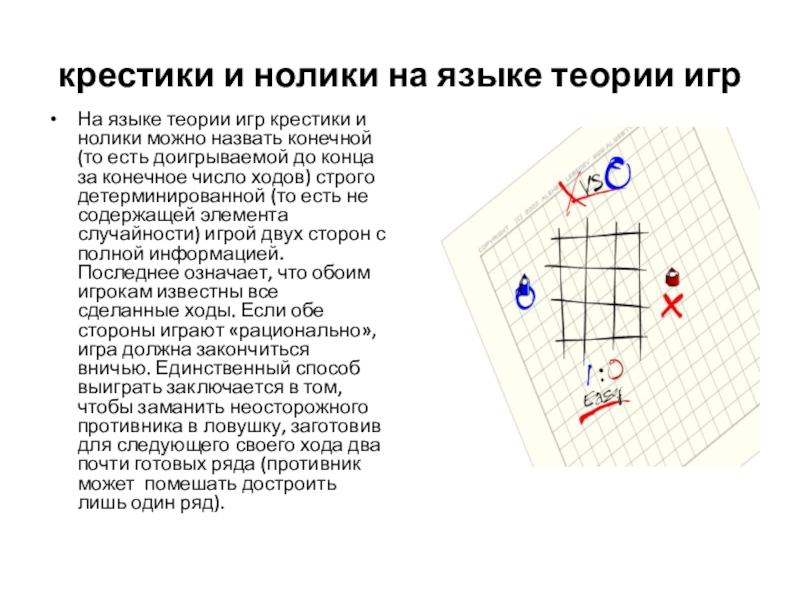
Слайд 7крестики и нолики на языке теории игр
На языке теории игр
Слайд 8Рациональность игроков
Представим себе идеального игрока, который в любой игровой ситуации принимает
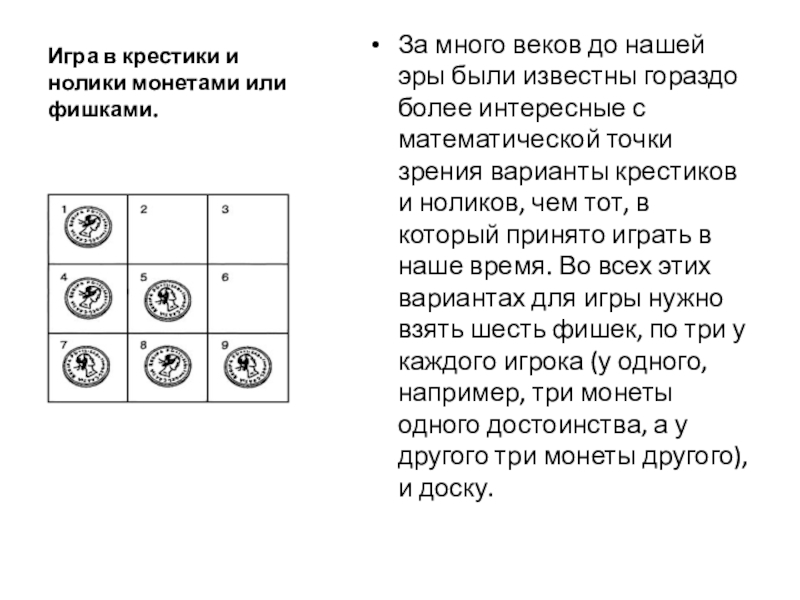
Слайд 9Игра в крестики и нолики монетами или фишками.
За много веков до
Слайд 10Игра «крестики-нолики» имеет древнее происхождение
Ее родиной является
Современное название этой игры – «Рэндзю», что в переводе с китайского значит «нить жемчуга».
В 270 г до н.э. игра была завезена в Японию, и там получила свое второе рождение.
В 1906 году была создана Токийская Ассоциация Рэндзю. С этих пор игра стала «спортивной» игрой. Постепенно игра вышла и на международный уровень
Слайд 11
Правила игры крестики-нолики
Основные термины и определения
РЯД - Набор камней одного
Процесс игры
Два игрока (Черные и Белые), поочередно, размещают камни своего цвета, по одному за ход, на пересечениях пустой игровой доски, которая состоит из 15 горизонтальных и 15 вертикальных линий. Первый ход всегда делают Черные в центр доски.
Слайд 12
Играют два соперника: один чёрными фишками (камнями), его соперник — белыми. Игра
Игроки делают ходы по очереди. Первыми ходят чёрные. Каждым ходом игрок выставляет на доску, в точку пересечения линий, один камень своего цвета. Побеждает тот, кто сможет первым построить непрерывный ряд из пяти камней своего цвета — по горизонтали, по вертикали или в диагональном направлении.
Слайд 13
60-е годы – игра «тико»
Известно много разновидностей крестиков и ноликов, в
В шестидесятые годы появилась игра «тико» — разновидность крестиков и ноликов, для которой нужна доска размером пять клеток на пять. Каждый из игроков по очереди выставляет свои четыре фишки, а затем передвигает их на одну клетку в любом направлении. Выигрывает тот, кто сумеет либо поставить свои четыре фишки в ряд (по горизонтали, вертикали или диагонали), либо выстроит их в виде квадрата на четырех клетках с общей вершиной.
Играть в крестики и нолики можно и без фишек, от этого игра не становится менее увлекательной. Рассмотрим, например, игру в крестики и нолики «наоборот» — тоу-так-тик (это название предложил М. Шоделл). Играют в нее, как в обычные крестики и нолики, но тот, кто первым закончит ряд из трех знаков, не выигрывает, а проигрывает. В игре тоу-так-тик у второго игрока имеется бесспорное преимущество. Первый может закончить вничью, лишь заняв первым же ходом центр, а в дальнейшем повторив по симметрии все ходы противника.
Слайд 14Тик-Так-Тоу
На первый взгляд кажется непонятным, что может так увлекать в этой
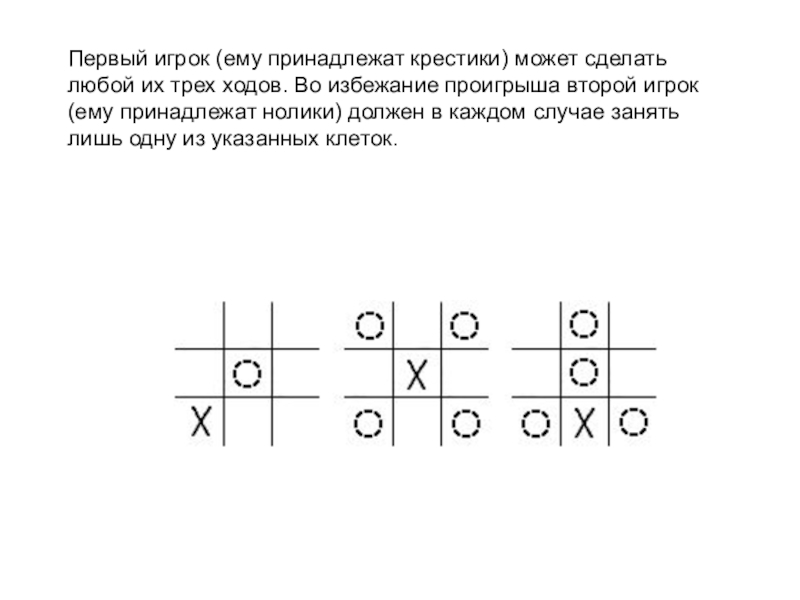
Слайд 15Первый игрок (ему принадлежат крестики) может сделать любой их трех ходов.
Слайд 16Дерево игровых ситуаций
Дерево игровых ситуаций для игры крестики-нолики, где
Слайд 18Фрагмент дерева игры «крестики-нолики»
В начальной позиции фрагмента игроки сделали по 3
Слайд 20
Алгоритм Цермело-Куна.
В позиционных играх главным вопросом является выбор хода. Какой
Для таких игр нет особого смысла выписывать вектор выигрышей для каждой терминальной позиции. Достаточно указать лишь выигрыш одного какого-нибудь игрока, например первого. Выигрыш второго игрока всегда равен выигрышу первого, взятому с обратным знаком.
Назовем оценкой позиции выигрыш, гарантированный в ней первому игроку, то есть для терминальных позиций . В частности для позиций нижнего уровня на рис 1 оценки этих позиций равны (слева направо): 0, 1, 0, 1.
Слайд 22Что такое выигрышная стратегия?
Позиции, в которых выигрывает тот, кто ходит
Игрок ''выигрывает'' в данной позиции значит, что он имеет возможность ходить так, и так отвечать на ходы противника, чтобы выиграть у него, независимо от того, как противник будет ходить. Эта возможность + описание того, как нужно отвечать на ходы соперника, называется выигрышной стратегией. Другими словами, если игрок умный и ходит первым из выигрышной позиции, то он выиграет. Но как бы ни был умён игрок, он может проиграть, если будет ходить первым из проигрышной позиции.
Слайд 23Задача Тема: Теория игр Классы: 7,8,9 Докажите, что в
Решение
Пусть первый игрок первым ходом ставит крестик в центр поля. У второго игрока есть две различные возможности: поставить нолик в угол или в середину боковой стороны. Как несложно проверить перебором, в каждом из этих случаев первый игрок может не допустить победы второго.
Слайд 24 Родственные игры
5 в ряд. Играют на бесконечном поле (либо на
Гомоку. Игра «5 в ряд» на доске 19х19 или 15х15 линий. Фолов нет. Построение длинного ряда не приносит победы ни одной из сторон.
5 в ряд с центральным запретным квадратом (ЦЗК). Другое название — «свободное рэндзю». На Западе именно эту разновидность игры называют «5 в ряд». Игра по правилам гомоку (фолов нет, длинный ряд не приносит победы) на доске 15х15 линий. Дополнительное правило: второй ход чёрных (то есть третий ход в партии) должен быть сделан за пределами центрального квадрата 5х5.
Пента. 5 в ряд на доске 19х19. Ряд из двух камней, закрытый с двух сторон камнями противника, становится «добычей» и снимается с доски. Второй ход чёрных делается за пределы центрального квадрата 5х5. Выигрывает тот, кто первым построил ряд из 5 или более камней, либо первым захватил 5 добыч. Пента — упрощённый вариант японской игры нинуки-рэндзю, распространённой в Японии в первой половине XX века.
Connect6 Интересная попытка уйти от искусственных ограничений рэндзю, уравняв возможности чёрных и белых за счёт порядка ходов. Игра идёт на доске 19×19, победа достигается построением ряда из шести камней или более. На первом ходе чёрные выставляют один камень, далее на каждом ходе игрок выставляет не один, а два камня за ход.
Слайд 25Вывод:
Анализ даже весьма простых игр показывает, что идеальный
Слайд 26 ПРИЛОЖЕНИЕ: "Крестики-нолики 3D" - победитель конкурсной программы специализированной выставки "Игрушка 2007" в
Итак, как это выглядит?
Вообще-то, игру можно было назвать "Шарики-шарики". Никаких крестиков и ноликов здесь нет. Вместо них - красные и синие шарики 1, 5 см. Но поскольку использован принцип известной нетленной головоломки, название игры полностью себя оправдывает.
Роль «крестиков» и «ноликов» исполняют разноцветные шарики. Задача игроков – закрыть как можно больше линий шариками «своего» цвета.
Линиями в Настольной игре Крестики-нолики 3D считаются:
- Горизонтали на верхнем, среднем и нижнем ярусе.
- Вертикали по всему объему куба.
- Диагонали, которые идут от верхних вершин куба через его центр к нижним вершинам.
- Диагонали каждого яруса.
- Диагонали каждой грани.
- Линии, соединяющие середины противоположных ребер.