- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему:Графы в архитектуре
Содержание
- 1. ПРезентация на тему:Графы в архитектуре
- 2. Введение Теория графов — раздел дискретной математики,
- 3. История возникновения Родоначальником теории графов принято считать
- 4. Задача о Кенигсбергских мостахЗадача состоит в том,
- 5. Задача о четырех краскахТеорема о четырех красках
- 6. Слайд 6
- 7. Задача о трех домах и трех колодцахИмеется
- 8. Основные понятия теории графовГрафом называется совокупность двух
- 9. Применение теории графов в архитектуреС использованием аппарата
- 10. ЗаключениеГрафы – это замечательные математические объекты, с
- 11. Спасибо за внимание!
Введение Теория графов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами.Граф (англ. graph) — основной объект изучения математической теории графов, совокупность непустого множества вершин и наборов
Слайд 2Введение
Теория графов — раздел дискретной математики, изучающий свойства графов. В
общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами.
Граф (англ. graph) — основной объект изучения математической теории графов, совокупность непустого множества вершин и наборов пар вершин (связей между вершинами).
Множество — одно из ключевых понятий математики, в частности, теории множеств и логики.
Граф (англ. graph) — основной объект изучения математической теории графов, совокупность непустого множества вершин и наборов пар вершин (связей между вершинами).
Множество — одно из ключевых понятий математики, в частности, теории множеств и логики.
Слайд 3История возникновения
Родоначальником теории графов принято считать математика Леонарда Эйлера (1707
– 1783). Однако теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.
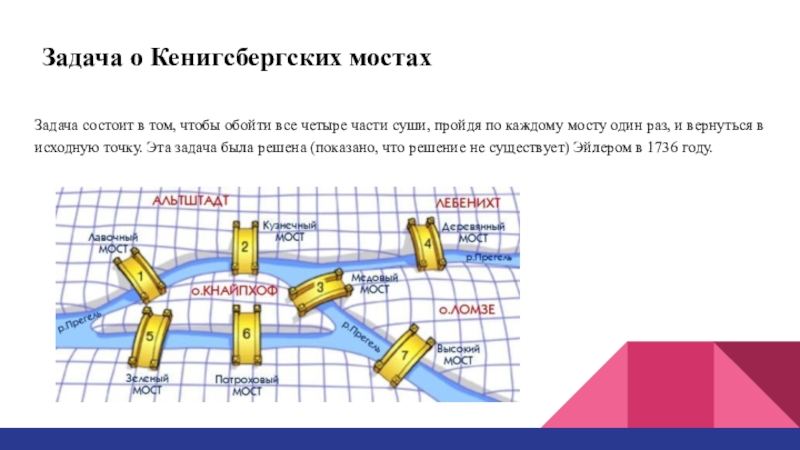
Слайд 4Задача о Кенигсбергских мостах
Задача состоит в том, чтобы обойти все четыре
части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку. Эта задача была решена (показано, что решение не существует) Эйлером в 1736 году.
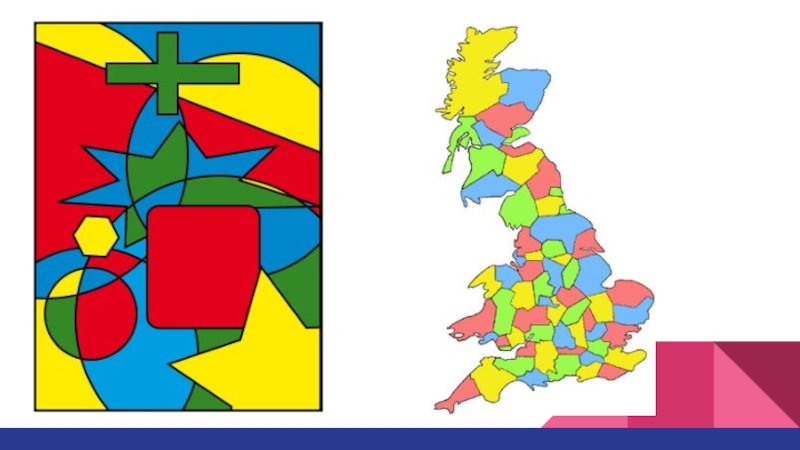
Слайд 5Задача о четырех красках
Теорема о четырех красках утверждает, что всякую расположенную
на сфере карту можно раскрасить не более чем четырьмя цветами так, чтобы любые две области с общим участком границы были раскрашены в разные цвета.
Эта теорема была сформулирована Френсисом Гутри в 1852 году, однако доказать ее удалось лишь в 1976 году Кеннетом Аппелем и Вольфганом Хакеном. Была представлена демонстрация того, что существует набор из 1936 карт, ни один из которых не может содержать карту меньшего размера, которая опровергла бы теорему.
Эта теорема была сформулирована Френсисом Гутри в 1852 году, однако доказать ее удалось лишь в 1976 году Кеннетом Аппелем и Вольфганом Хакеном. Была представлена демонстрация того, что существует набор из 1936 карт, ни один из которых не может содержать карту меньшего размера, которая опровергла бы теорему.
Слайд 7Задача о трех домах и трех колодцах
Имеется три дома и три
колодца, каким-то образом расположенные на плоскости. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались. Эта задача была решена (показано, что решение не существует) Куратовским в 1930 году.
Слайд 8Основные понятия теории графов
Графом называется совокупность двух множеств – непустого множества
(множества вершин) и множества E двухэлементных подмножеств множества – множество ребер).
Ориентированный граф (сокращенно Орграф)G – это упорядоченная пара где V-непустое множество вершин или узлов, и А-множество(упорядоченных) пар различных вершин ,называемых дугами или ориентированными ребрами.
Смешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G:(V,E,A),где V,E и A определены так же ,как выше.
Ориентированный граф (сокращенно Орграф)G – это упорядоченная пара где V-непустое множество вершин или узлов, и А-множество(упорядоченных) пар различных вершин ,называемых дугами или ориентированными ребрами.
Смешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G:(V,E,A),где V,E и A определены так же ,как выше.
Слайд 9Применение теории графов в архитектуре
С использованием аппарата теории графов очень удобно
описывать любые архитектурно-планировочные, функциональные и другие схемы и объекты. Так, любая фигура, схема, чертеж, описанные набором точек и соединяющих их отрезков, могут рассматриваться как граф, в котором каждая вершина имеет соответствующую пару (или тройку) координат, указывающих на физическую реализацию данного объекта в двух- или трехмерном пространстве. К этому только надо будет добавить еще матрицу связностей, указывающую на порядок связи вершин графа между собой.
Слайд 10Заключение
Графы – это замечательные математические объекты, с помощью, которых можно решать
математические, экономические и логические задачи. Также можно решать различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Сама теория графов является частью как топологии, так и комбинаторики.
Таким образом, изучение теории графов немаловажно для всестороннего развития студента .
Таким образом, изучение теории графов немаловажно для всестороннего развития студента .