Тригонометриялық теңдеулерді шешу
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тригонометриялық теңдеулерді шешу тақырыбына презентация
Содержание
- 1. Тригонометриялық теңдеулерді шешу тақырыбына презентация
- 2. Үй жұмысын тексеру118 а) 1-балл
- 3. Үй жұмысын тексеру 2-балл
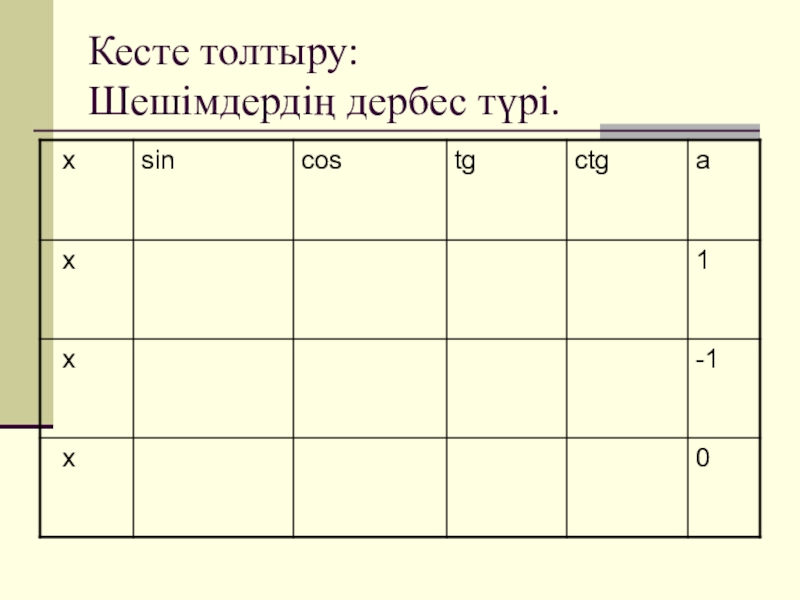
- 4. Кесте толтыру: Шешімдердің дербес түрі.
- 5. Өз жауабыңды өзің тексеріп көр. 12балл
- 6. математикалық домино
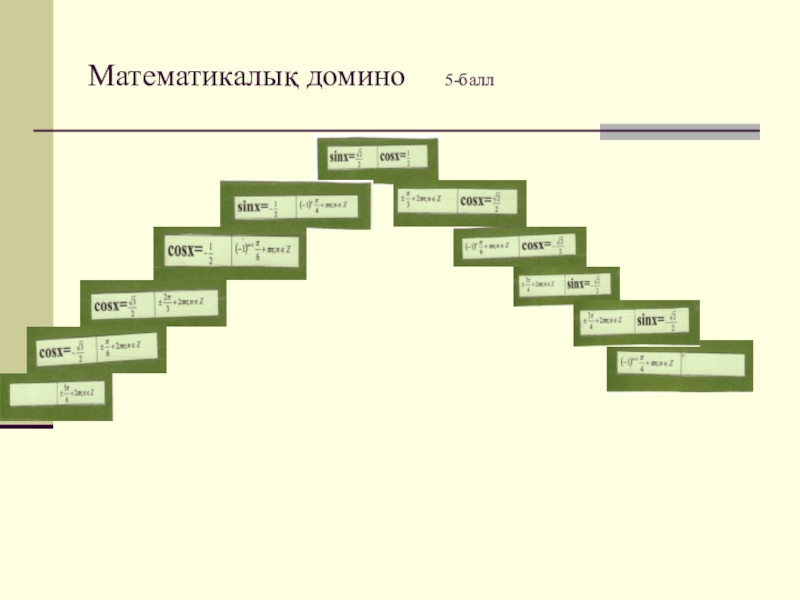
- 7. Математикалық домино 5-балл
- 8. Тест тапсырмалары:
- 9. ТЕСТ КІЛТІ:
- 10. ОЙЫН Әрбір дұрыс жауап 1-баллЖАЛҒАСТЫРУ
- 11. Тригонометриялық функциялардың қосындысы мен айырымы формулалары
- 12. Екі еселенген бұрыштың формулаларыsin2α═sin2α═2sinαcosαcos2α=cos2 α ═cos²α- sin²α=2cos²α-1=1-2
- 13. Аргументтерді қосу мен азайту формулаларыcos(α+β)═cos(α+β)═cosαcosβ-sinαsinβcos(α-β)═cos(α-β)═cosαcosβ+sinαsinβsin(α+β)═sin(α+β)═sinαcosβ+cosαsinβsin(α-β)═sin(α-β)═sinαcosβ-cosαsinβ
- 14. Алгоритм құрастыру: 2tgx-ctgx-1=0 1.Біртектес тригонометриялық функцияға келтіріп аламыз2.Белгілеу енгіземіз3. Алгебралық теңдеуді шешеміз4.Кері белгілейміз5.Қарапайым тригонометрия-лық теңдеуді шешеміз
- 15. Алгоритм құрастыру: 3cos2x=7sinx1.Тригонометриялық формулалар арқылы бірдей аргументті,біртек-тес
- 16. Қатесін табыңдар
- 17. Қатесін табыңдар
- 18. Қатесін табыңдар
- 19. Тригонометриялық теңдеулерді шешіңдер 5-баллcos²x-cosx=07sin²x-4sin2x+cos²x=0cos²x-3sinxcosx=-1cos4x+2cos²x-1=01+cosx-cosx/2=0
- 20. Қорытынды:“5”-бағасы,егер 36 балдан көп болса“4”-бағасы, егер 29-35 балл“3”- бағасы ,егер 21-28 балл20 балдан төмен -“2” бағасы
- 21. Үй жұмысыТригонометриялық теңдеулерді шешу125126
Үй жұмысын тексеру118 а) 1-балл
Слайд 1Сабақтың тақырыбы:
Мақсаты:
Тригонометриялық теңдеулерді шешудің әртүрлі тәсілдерін үйрену, тригонометриялық формулаларды қолдана білу
.Өзін-өзі бағалай білу
Слайд 11Тригонометриялық функциялардың қосындысы мен айырымы формулалары
=Sinα+sinβ
=sinα-sin β
=cosα+cosβ
=cosα-cosβ
=tgα +tg β =tgα -tg β
=sinα-sin β
=cosα+cosβ
=cosα-cosβ
=tgα +tg β =tgα -tg β
Слайд 12Екі еселенген бұрыштың формулалары
sin2α═
sin2α═2sinαcosα
cos2α=
cos2 α ═cos²α- sin²α=2cos²α-1=1-2 sin²α
=tg2 α
Слайд 13Аргументтерді қосу мен азайту формулалары
cos(α+β)═
cos(α+β)═cosαcosβ-sinαsinβ
cos(α-β)═
cos(α-β)═cosαcosβ+sinαsinβ
sin(α+β)═
sin(α+β)═sinαcosβ+cosαsinβ
sin(α-β)═
sin(α-β)═sinαcosβ-cosαsinβ
Слайд 14Алгоритм құрастыру:
2tgx-ctgx-1=0
1.Біртектес тригонометриялық
функцияға келтіріп аламыз
2.Белгілеу енгіземіз
3. Алгебралық теңдеуді шешеміз
4.Кері белгілейміз
5.Қарапайым
тригонометрия-
лық теңдеуді шешеміз
лық теңдеуді шешеміз
Слайд 15Алгоритм құрастыру:
3cos2x=7sinx
1.Тригонометриялық формулалар
арқылы бірдей аргументті,біртек-
тес функцияға келтіріп аламыз
2.Белгілеу енгіземіз
3. Алгебралық
теңдеуді шешеміз
4.Кері белгілейміз
5.Қарапайым тригонометрия-
лық теңдеуді шешеміз
4.Кері белгілейміз
5.Қарапайым тригонометрия-
лық теңдеуді шешеміз
Слайд 19Тригонометриялық теңдеулерді шешіңдер 5-балл
cos²x-cosx=0
7sin²x-4sin2x+cos²x=0
cos²x-3sinxcosx=-1
cos4x+2cos²x-1=0
1+cosx-cosx/2=0
Слайд 20Қорытынды:
“5”-бағасы,егер 36 балдан көп болса
“4”-бағасы, егер 29-35 балл
“3”- бағасы ,егер 21-28
балл
20 балдан төмен -“2” бағасы
20 балдан төмен -“2” бағасы