- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тетраэдр и параллелепипед
Содержание
- 1. Тетраэдр и параллелепипед
- 2. Тетраэдр, или треугольная пирамида, - простейший из
- 3. Типы тетраэдров:Равногранный тетраэдрОртоцентрический тетраэдрПрямоугольный тетраэдрПравильный тетраэдрКаркасный тетраэдр Соразмерный тетраэдрИнцентрический тетраэдр
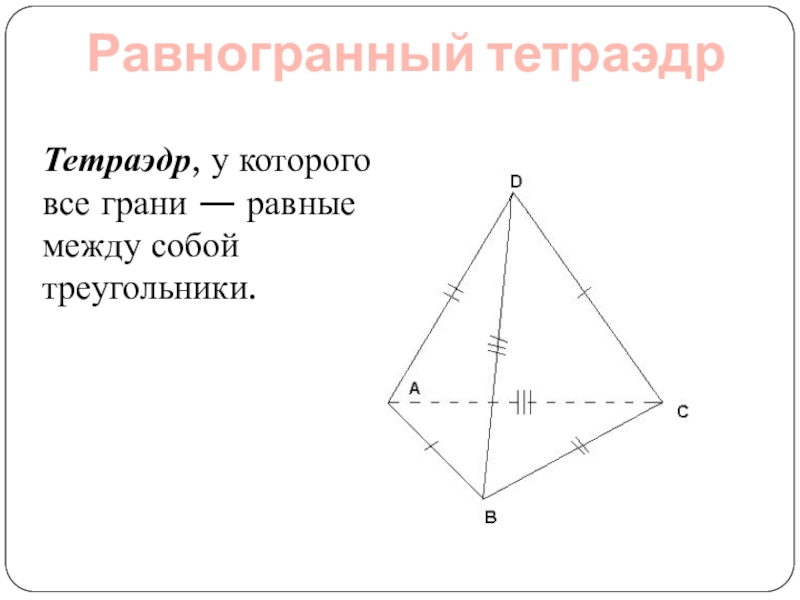
- 4. Равногранный тетраэдрТетраэдр, у которого все грани — равные между собой треугольники.
- 5. Ортоцентрический тетраэдрТетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
- 6. Прямоугольный тетраэдрТетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой.
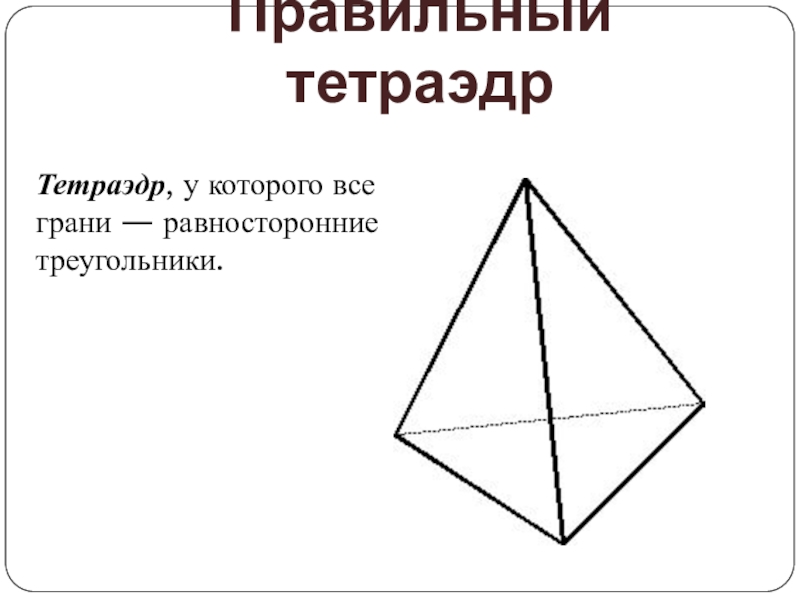
- 7. Правильный тетраэдрТетраэдр, у которого все грани — равносторонние треугольники.
- 8. Каркасный тетраэдр Тетраэдр, отвечающий любому из следующих
- 9. Соразмерный тетраэдрТетраэдр, бивысоты которого равны.Это определение можно
- 10. Инцентрический тетраэдрТетраэдр, у которого отрезки, соединяющие вершины
- 11. Свойства тетраэдра:Параллельные плоскости, проходящие через пары скрещивающихся
- 12. Тетраэдры в живой природеНекоторые плоды, находясь вчетвером
- 13. Тетраэдры в техникеТетраэдр образует жёсткую, статически определимую
- 14. Слайд 14
- 15. Параллелепипед
- 16. Что такое «параллелепипед» ?Параллелепипед- это призма, основанием
- 17. Типы параллелепипедов: Прямоугольный параллелепипедПрямой параллелепипед Наклонный параллелепипед
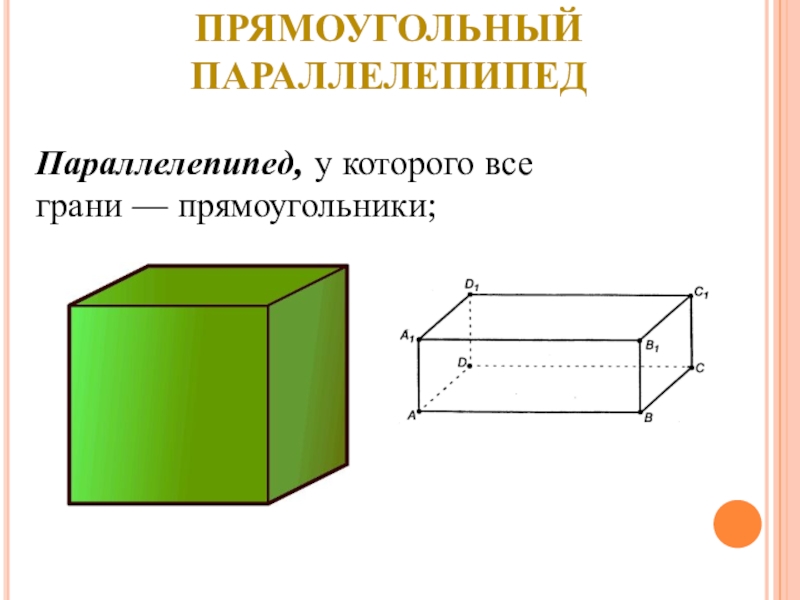
- 18. Прямоугольный параллелепипедПараллелепипед, у которого все грани — прямоугольники;
- 19. Прямой параллелепипедПараллелепипед, у которого 4 боковые грани — прямоугольники;
- 20. Наклонный параллелепипедПараллелепипед, боковые грани которого не перпендикулярны основаниям.
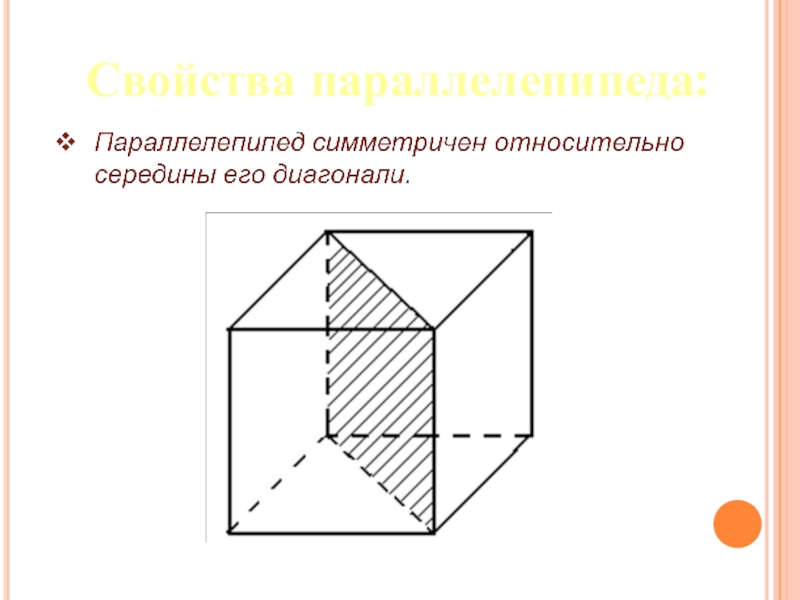
- 21. Свойства параллелепипеда:
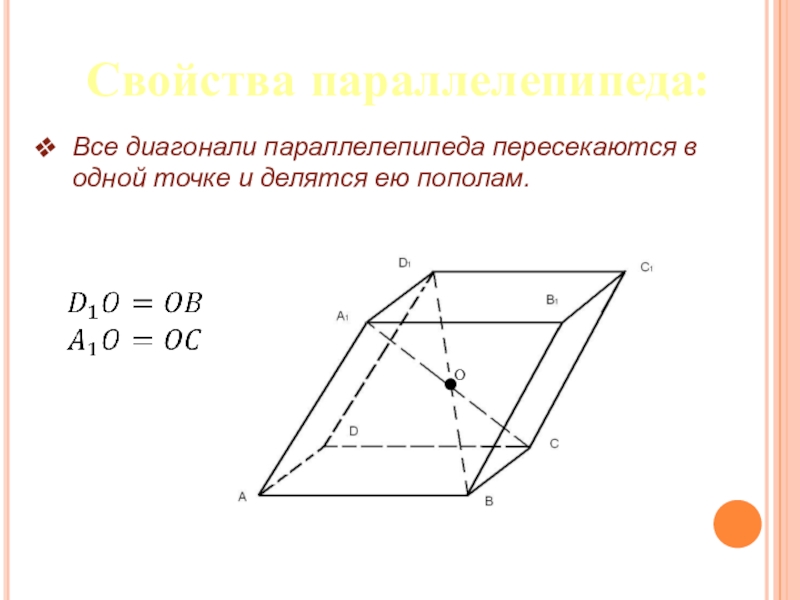
- 22. Свойства параллелепипеда:Все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.О
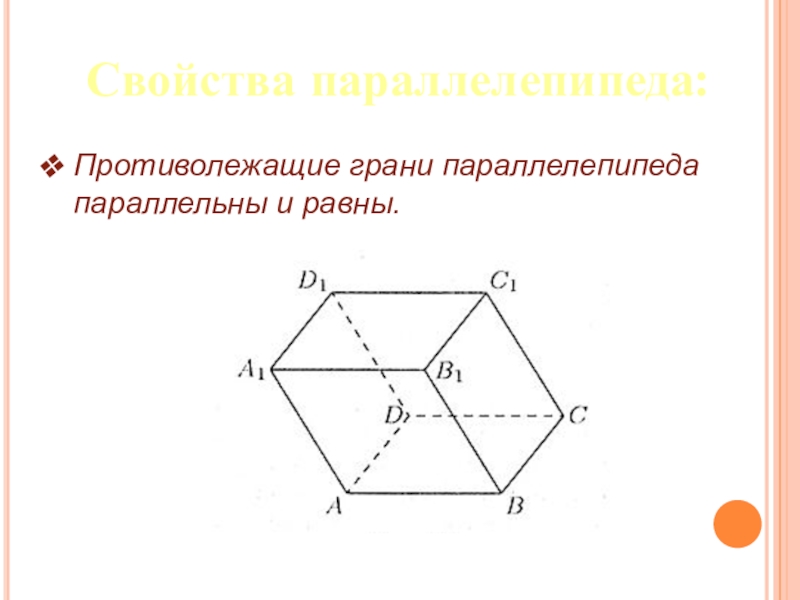
- 23. Свойства параллелепипеда:Противолежащие грани параллелепипеда параллельны и равны.
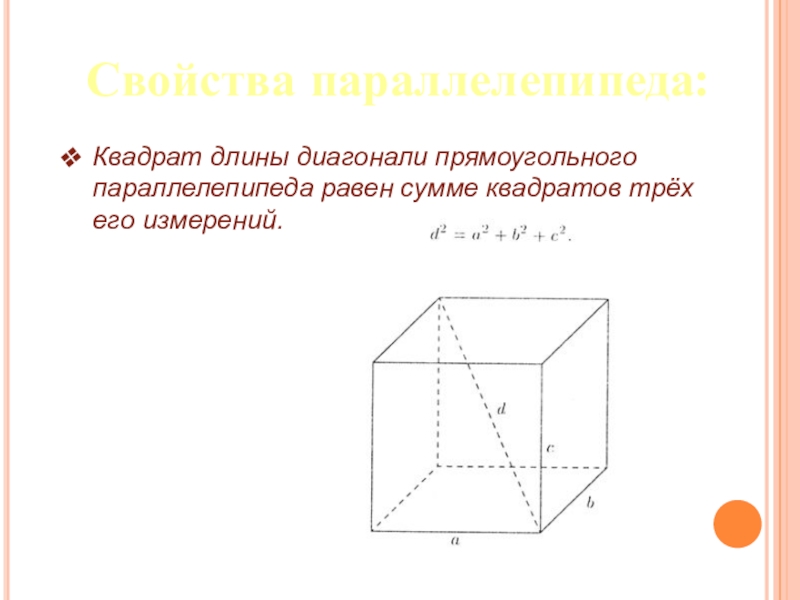
- 24. Свойства параллелепипеда:Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
- 25. Параллелепипед в жизни
- 26. Из параллелепипедов можно собрать один большой параллелепипед
- 27. Слайд 27
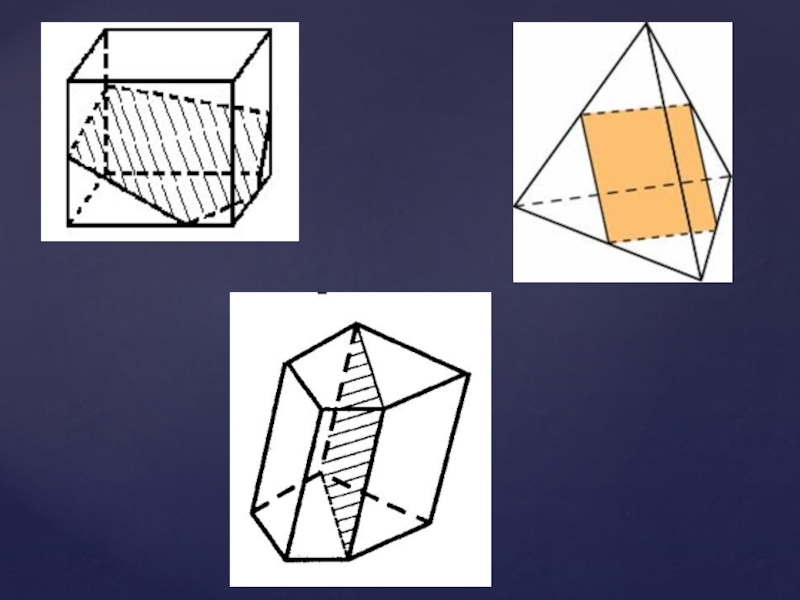
- 28. Построение плоских сечений
- 29. В стереометрии часто приходится рассматривать сечения фигур, в частности многогранников, различными плоскостями.
- 30. Сечение выпуклого многогранника есть выпуклый плоский
- 31. Слайд 31
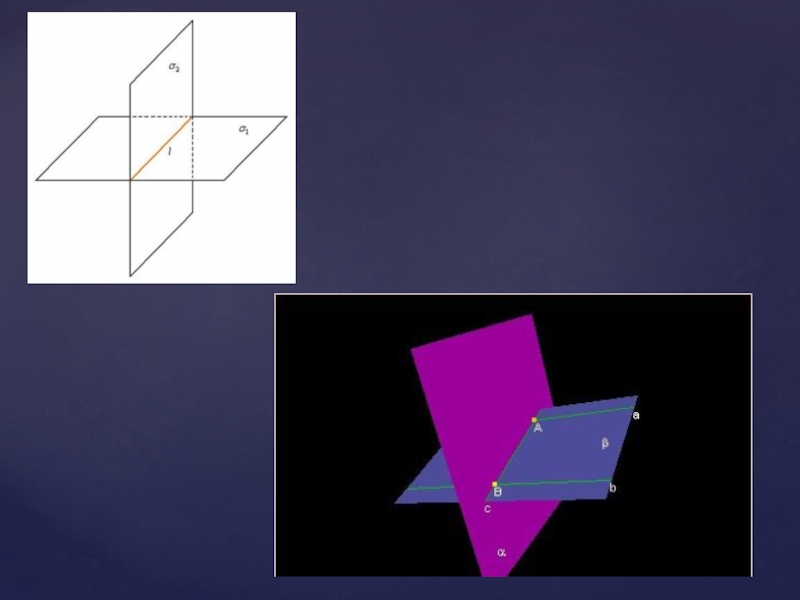
- 32. Для построения прямой пересечения двух плоскостей обычно находят две её точки и проводят через них прямую
- 33. Слайд 33
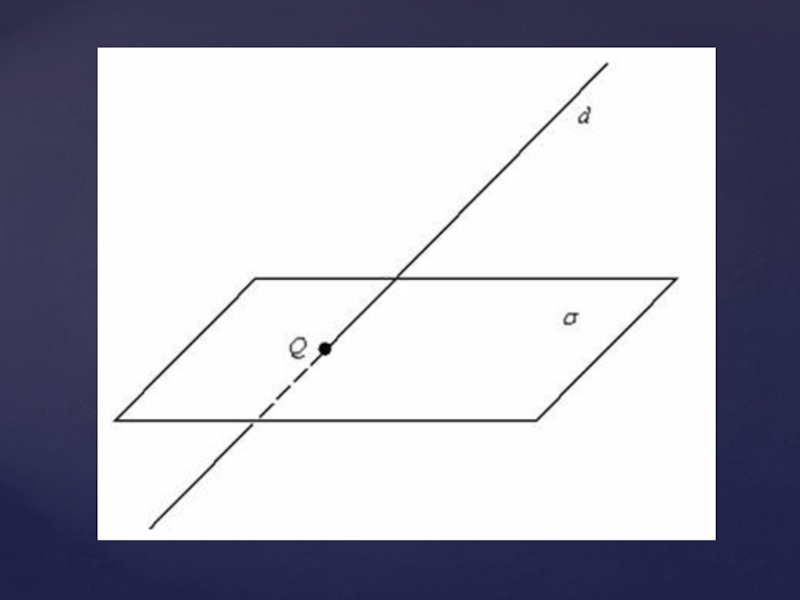
- 34. Для построения точки пересечения прямой и плоскости
- 35. Слайд 35
- 36. Обобщение ранее перечисленного:Для построения сечения нужно найти
- 37. Метод следов
- 38. Алгоритм построения методом следов: Выяснить имеются ли
- 39. Комбинированный метод
- 40. Суть комбинированного метода построения сечений многогранников состоит
- 41. Пример:На ребрах AB и AD пирамиды MABCD
- 42. 1) Ясно, что основным следом плоскости PQR
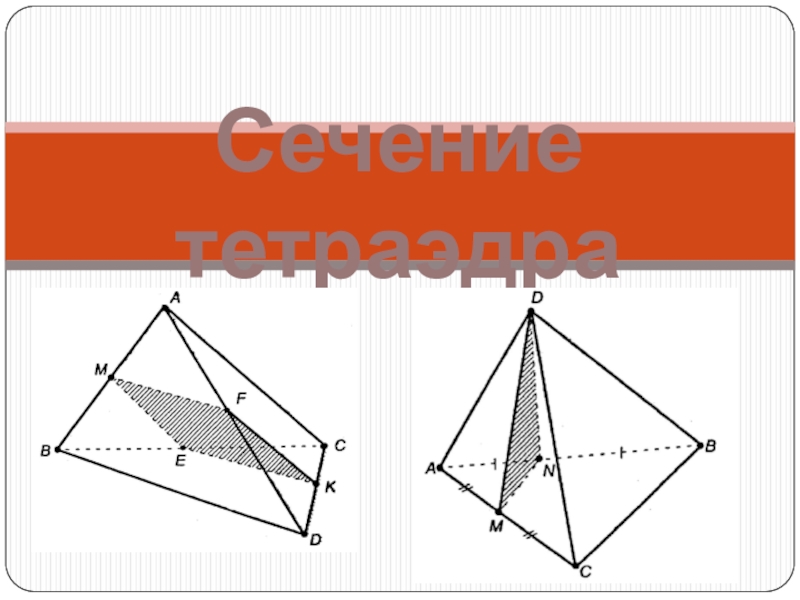
- 43. Сечение тетраэдра
- 44. Секущей плоскостью тетраэдра называется любая плоскость, по
- 45. Правило построения сечения тетраэдра:1) проводим прямые через
- 46. Слайд 46
- 47. Сечение параллелепипеда
- 48. Секущая плоскость пересекает противоположные грани параллелепипеда по параллельным отрезкам.
- 49. Слайд 49
- 50. Решение задач на построение сечений тетраэдра и параллелепипеда.
- 51. Примеры задач из учебника
- 52. Задача №1На рёбрах AB, BD и CD
- 53. РешениеПостроим сначала прямую, по которой плоскость MNP
- 54. Следовательно, эти плоскости пересекаются по прямой ME.
- 55. Если прямые NP и BC параллельны, то
- 56. Задача №2Точка М лежит на боковой грани
- 57. РешениеТ.к. секущая плоскость параллельна плоскости ABC, то
- 58. Обозначим буквами P и Q точки пересечения
- 59. Задача №3На рёбрах параллелепипеда даны три точки A, B и C. Построить сечение параллелепипеда плоскостью ABC.
- 60. РешениеПостроение искомого сечения зависит от того, на
- 61. Если три данные точки A, B и
- 62. Более трудный случай, когда данные точки A,
- 63. Эта прямая пересекается с рёбрами нижнего основания
- 64. Решение задач на построение сечений
- 65. Задача №1Построить сечение тетраэдра DABC плоскостью, проходящей
- 66. РешениеL
- 67. Задача №2
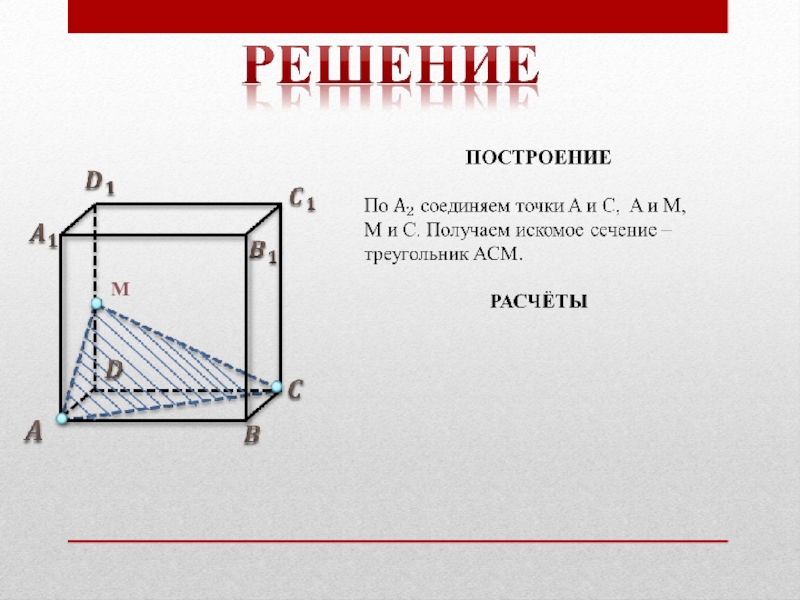
- 68. M
- 69. Задача №3
- 70. Слайд 70
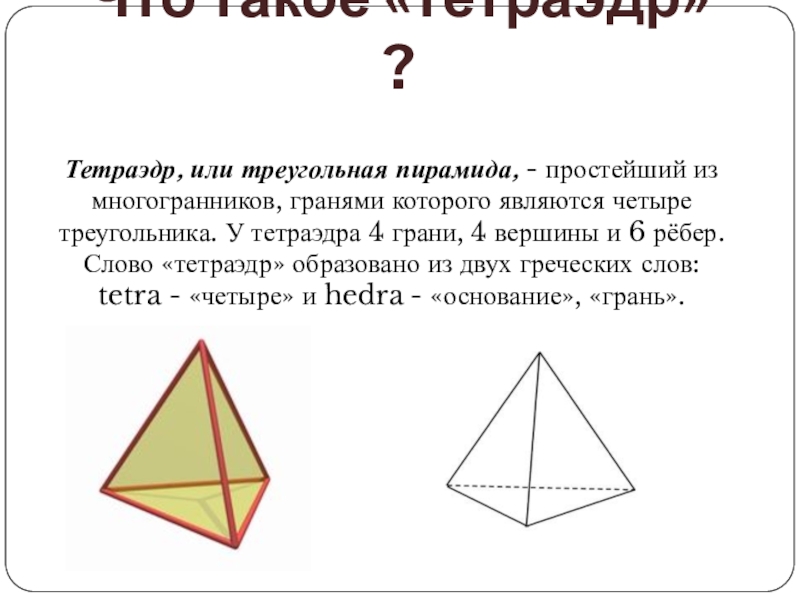
Тетраэдр, или треугольная пирамида, - простейший из многогранников, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Слово «тетраэдр» образовано из двух греческих слов: tetra - «четыре» и hedra -
Слайд 2Тетраэдр, или треугольная пирамида, - простейший из многогранников, гранями которого являются
четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Слово «тетраэдр» образовано из двух греческих слов:
tetra - «четыре» и hedra - «основание», «грань».
Что такое «тетраэдр» ?
Слайд 3Типы тетраэдров:
Равногранный тетраэдр
Ортоцентрический тетраэдр
Прямоугольный тетраэдр
Правильный тетраэдр
Каркасный тетраэдр
Соразмерный тетраэдр
Инцентрический тетраэдр
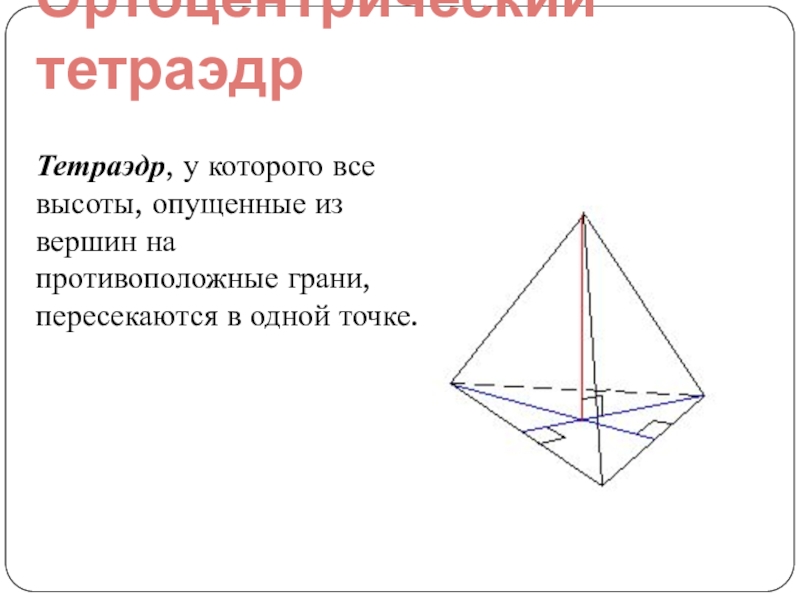
Слайд 5Ортоцентрический тетраэдр
Тетраэдр, у которого все высоты, опущенные из вершин на противоположные
грани, пересекаются в одной точке.
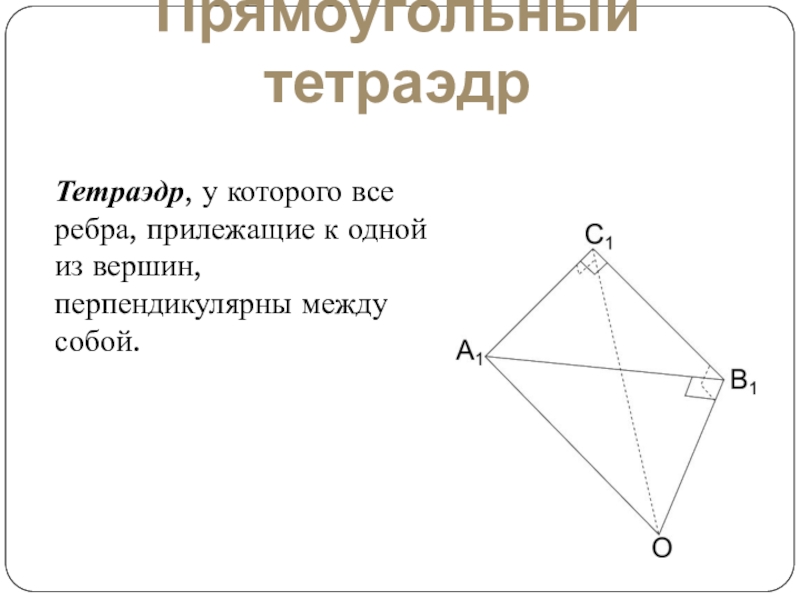
Слайд 6Прямоугольный тетраэдр
Тетраэдр, у которого все ребра, прилежащие к одной из вершин,
перпендикулярны между собой.
Слайд 8Каркасный тетраэдр
Тетраэдр, отвечающий любому из следующих условий:
существует сфера, касающаяся всех
ребер,
суммы длин скрещивающихся ребер равны,
суммы двугранных углов при противоположных ребрах равны,
окружности, вписанные в грани, попарно касаются,
все четырехугольники, получающиеся на развертке тетраэдра, — описанные,
перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
суммы длин скрещивающихся ребер равны,
суммы двугранных углов при противоположных ребрах равны,
окружности, вписанные в грани, попарно касаются,
все четырехугольники, получающиеся на развертке тетраэдра, — описанные,
перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
Слайд 9Соразмерный тетраэдр
Тетраэдр, бивысоты которого равны.
Это определение можно заменить любым из следующих:
Проекция
тетраэдра на плоскость, перпендикулярную любой бимедиане, есть ромб.
Грани описанного параллелепипеда равновелики.
Для каждой пары противоположных ребер тетраэдра плоскости, проведенные через одно из них и середину второго, перпендикулярны.
В описанный параллелепипед соразмерного тетраэдра можно вписать сферу.
Грани описанного параллелепипеда равновелики.
Для каждой пары противоположных ребер тетраэдра плоскости, проведенные через одно из них и середину второго, перпендикулярны.
В описанный параллелепипед соразмерного тетраэдра можно вписать сферу.
Слайд 10Инцентрический тетраэдр
Тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей,
вписанных в противоположные грани, пересекаются в одной точке.
Слайд 11Свойства тетраэдра:
Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный
около тетраэдра параллелепипед.
Все медианы тетраэдра пересекаются в одной точке, которая делит их в отношении 3:1, считая от вершины (теорема Коммандино). В этой же точке пересекаются и бимедианы тетраэдра, которые делятся ею пополам.
Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части.
Все медианы тетраэдра пересекаются в одной точке, которая делит их в отношении 3:1, считая от вершины (теорема Коммандино). В этой же точке пересекаются и бимедианы тетраэдра, которые делятся ею пополам.
Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части.
Слайд 12Тетраэдры в живой природе
Некоторые плоды, находясь вчетвером на одной кисти, располагаются
в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Слайд 13Тетраэдры в технике
Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из
стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр
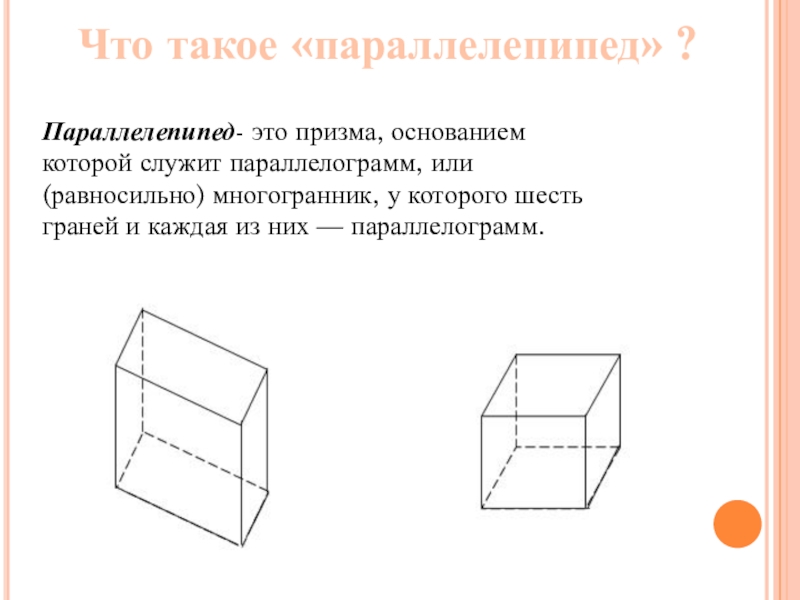
Слайд 16Что такое «параллелепипед» ?
Параллелепипед- это призма, основанием которой служит параллелограмм, или
(равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм.
Слайд 17Типы параллелепипедов:
Прямоугольный параллелепипед
Прямой
параллелепипед
Наклонный
параллелепипед
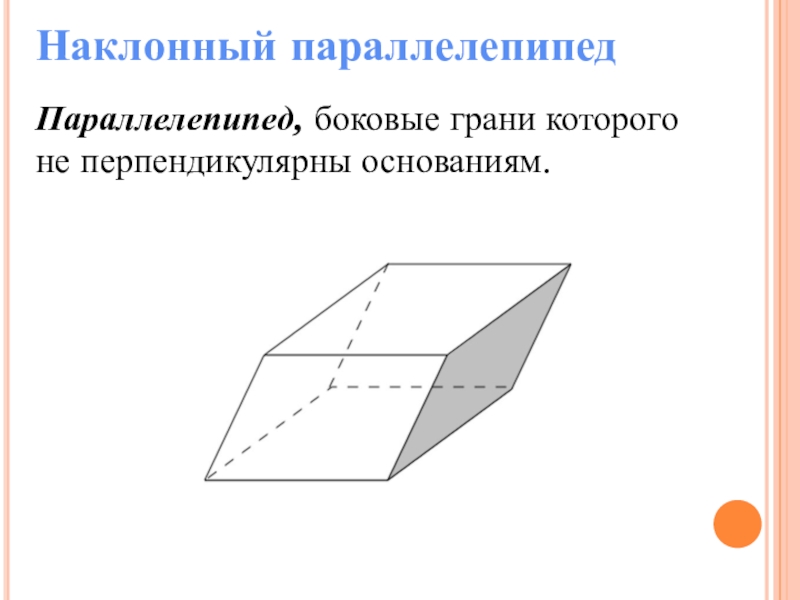
Слайд 20Наклонный параллелепипед
Параллелепипед, боковые грани которого не перпендикулярны основаниям.
Слайд 22Свойства параллелепипеда:
Все диагонали параллелепипеда пересекаются в одной точке и делятся ею
пополам.
О
Слайд 24Свойства параллелепипеда:
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его
измерений.
Слайд 26Из параллелепипедов можно собрать один большой параллелепипед при том, что между
ними не было пустот. Такая конструкция будет уже устойчивой. Не случайно, дома строят из кирпичей, имеющих форму именно параллелепипеда. Ни один строитель не станет строить дом из цилиндрических или шарообразных кирпичей. Доски тоже имеют форму параллелепипеда. Строительные блоки - тоже параллелепипеды. Когда маленькие дети играют в кубики, они убеждаются, что их можно хорошо ставить один на другой именно потому, что они имеют форму куба, т. е. того же параллелепипеда.
В нашей жизни многие предметы имеют форму параллелепипеда. И главное его назначение - устойчивость его конструкции. В целом, параллелепипед - очень нужная форма тела. Без него трудно обойтись.
В нашей жизни многие предметы имеют форму параллелепипеда. И главное его назначение - устойчивость его конструкции. В целом, параллелепипед - очень нужная форма тела. Без него трудно обойтись.
Слайд 29В стереометрии часто приходится рассматривать сечения фигур, в частности многогранников, различными
плоскостями.
Слайд 30Сечение выпуклого многогранника есть выпуклый плоский многоугольник, вершины которого в общем
случае являются точками пересечения секущей плоскости с ребрами многогранника, а стороны- линиями пересечения секущей плоскости с гранями.
Слайд 32Для построения прямой пересечения двух плоскостей обычно находят две её точки
и проводят через них прямую
Слайд 34Для построения точки пересечения прямой и плоскости находят в плоскости прямую,
пересекающую данную. Тогда искомая точка получается в пересечении найденной прямой с данной.
Слайд 36Обобщение ранее перечисленного:
Для построения сечения нужно найти прямые, по которым плоскость
сечения пересекается с плоскостями граней многогранника.
Для построения прямой пересечения плоскостей, как правило, находят две её точки, через них и проводят прямую пересечения.
Точки прямой пересечения (см. выше) отыскиваются как точки пересечения известной прямой, лежащей в одной плоскости, со второй плоскостью
Для построения такой точки пересечения (см. выше) данных прямой и плоскости в этой плоскости находят прямую, пересекающую данную,- искомая точка получается в пересечении этих прямых (на проекционном чертеже)
Для построения прямой пересечения плоскостей, как правило, находят две её точки, через них и проводят прямую пересечения.
Точки прямой пересечения (см. выше) отыскиваются как точки пересечения известной прямой, лежащей в одной плоскости, со второй плоскостью
Для построения такой точки пересечения (см. выше) данных прямой и плоскости в этой плоскости находят прямую, пересекающую данную,- искомая точка получается в пересечении этих прямых (на проекционном чертеже)
Слайд 38Алгоритм построения методом следов:
Выяснить имеются ли в одной грани две
точки сечения (если да, то через них можно провести сторону сечения).
Построить след сечения на плоскости основания многогранника. Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом).
Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани.
Построить след сечения на плоскости основания многогранника. Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом).
Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани.
Слайд 40Суть комбинированного метода построения сечений многогранников состоит в применении теорем о
параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.
Слайд 41Пример:
На ребрах AB и AD пирамиды MABCD зададим соответственно точки P
и Q - середины этих ребер, а на ребре MC зададим точку R. Построим сечение пирамиды плоскостью, проходящей через точки P, Q и R.
Слайд 421) Ясно, что основным следом плоскости PQR является прямая PQ.
2) Найдем
точку К, в которой плоскость МАС пересекает прямую PQ. Точки К и R принадлежат и плоскости PQR, и плоскости MAC. Поэтому, проведя прямую KR, мы получим линию пересечения этих плоскостей.
3) Найдем точку N=AC BD, проведем прямую MN и найдем точку F=KR MN.
4) Точка F является общей точкой плоскостей PQR и MDB, то есть эти плоскости пересекаются по прямой, проходящей через точку F. Вместе с тем так как PQ - средняя линия треугольника ABD, то PQ параллельна BD, то есть прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, то есть параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем прямую, параллельную прямой BD.
5) Дальнейшие построения понятны из рисунка. В итоге получаем многоугольник PQD'RB' - искомое сечение.
3) Найдем точку N=AC BD, проведем прямую MN и найдем точку F=KR MN.
4) Точка F является общей точкой плоскостей PQR и MDB, то есть эти плоскости пересекаются по прямой, проходящей через точку F. Вместе с тем так как PQ - средняя линия треугольника ABD, то PQ параллельна BD, то есть прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, то есть параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем прямую, параллельную прямой BD.
5) Дальнейшие построения понятны из рисунка. В итоге получаем многоугольник PQD'RB' - искомое сечение.
Слайд 44Секущей плоскостью тетраэдра называется любая плоскость, по обе стороны от которой
имеются точки данного тетраэдра.
Секущая плоскость пересекает тетраэдр по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.
Слайд 45Правило построения сечения тетраэдра:
1) проводим прямые через точки, лежащие в одной
плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
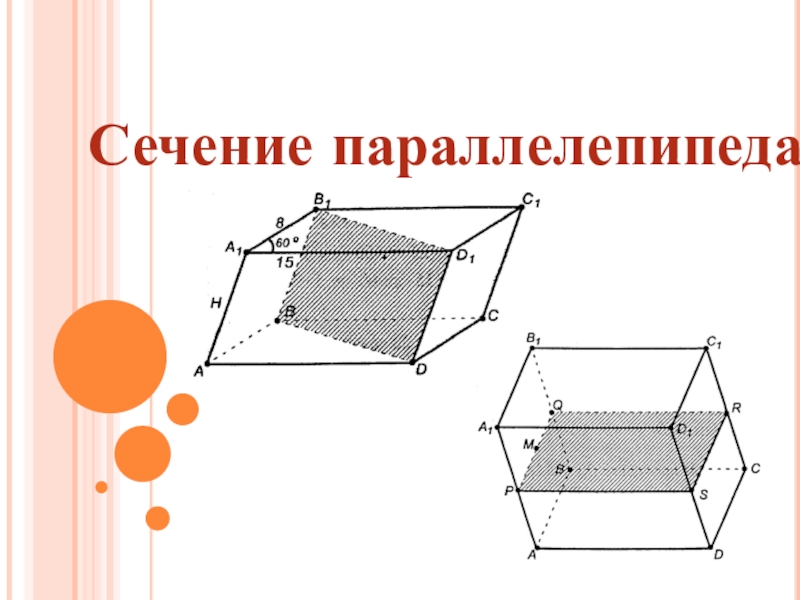
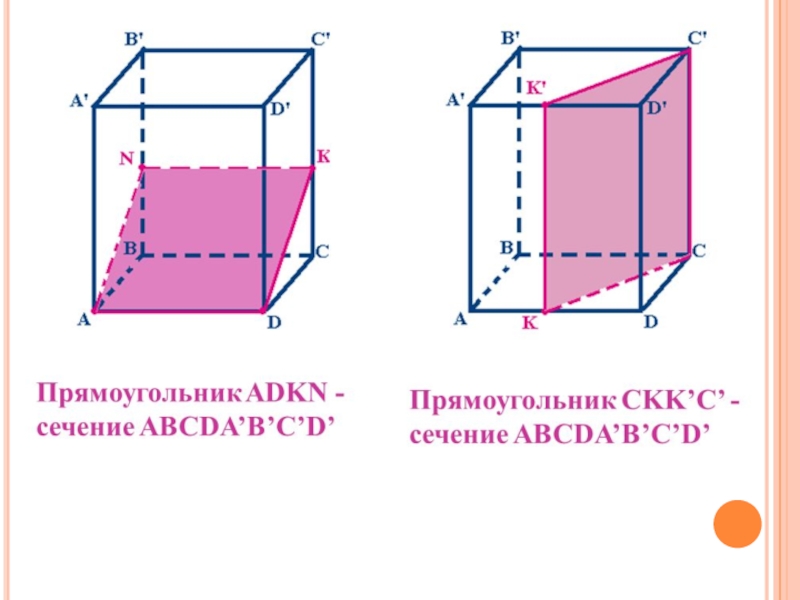
Слайд 48Секущая плоскость
пересекает
противоположные грани параллелепипеда
по параллельным
отрезкам.
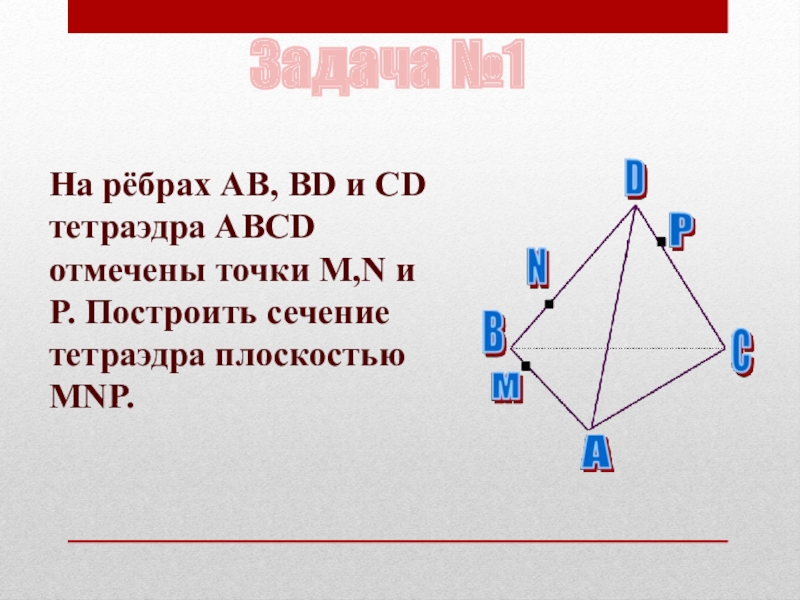
Слайд 52Задача №1
На рёбрах AB, BD и CD тетраэдра ABCD отмечены точки
M,N и P. Построить сечение тетраэдра плоскостью MNP.
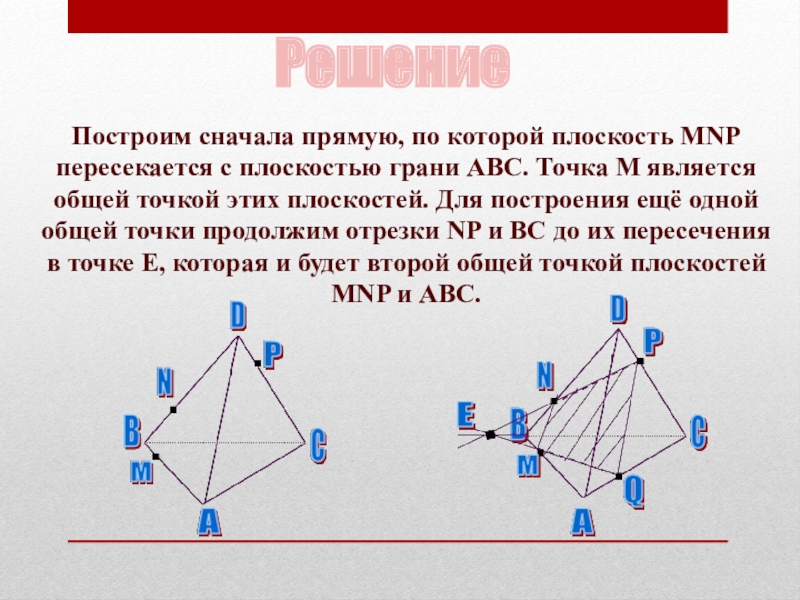
Слайд 53Решение
Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани
ABC. Точка М является общей точкой этих плоскостей. Для построения ещё одной общей точки продолжим отрезки NP и BC до их пересечения в точке Е, которая и будет второй общей точкой плоскостей MNP и ABC.
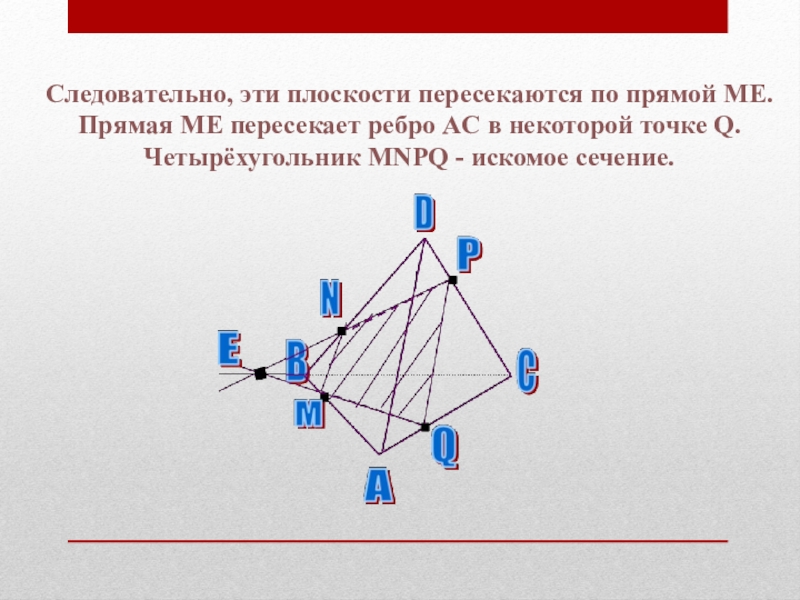
Слайд 54Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро
AC в некоторой точке Q. Четырёхугольник MNPQ - искомое сечение.
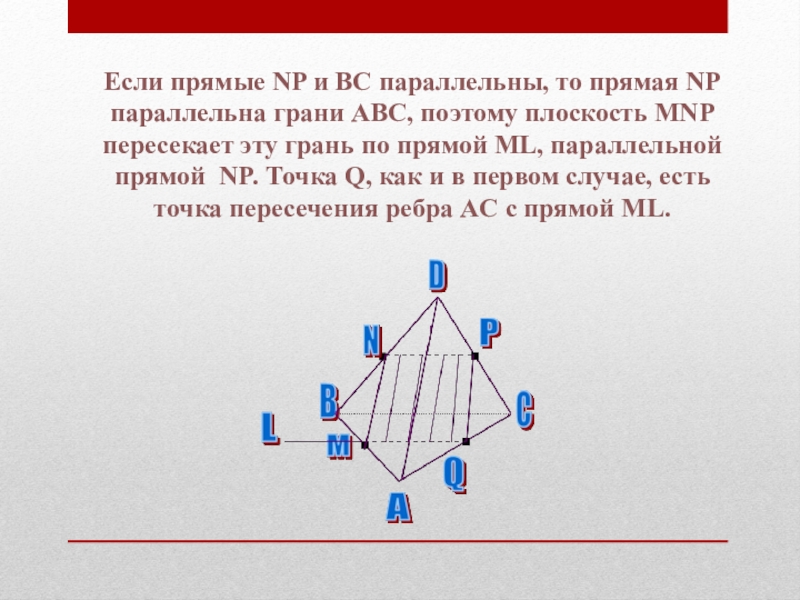
Слайд 55Если прямые NP и BC параллельны, то прямая NP параллельна грани
ABC, поэтому плоскость MNP пересекает эту грань по прямой ML, параллельной прямой NP. Точка Q, как и в первом случае, есть точка пересечения ребра AC с прямой ML.
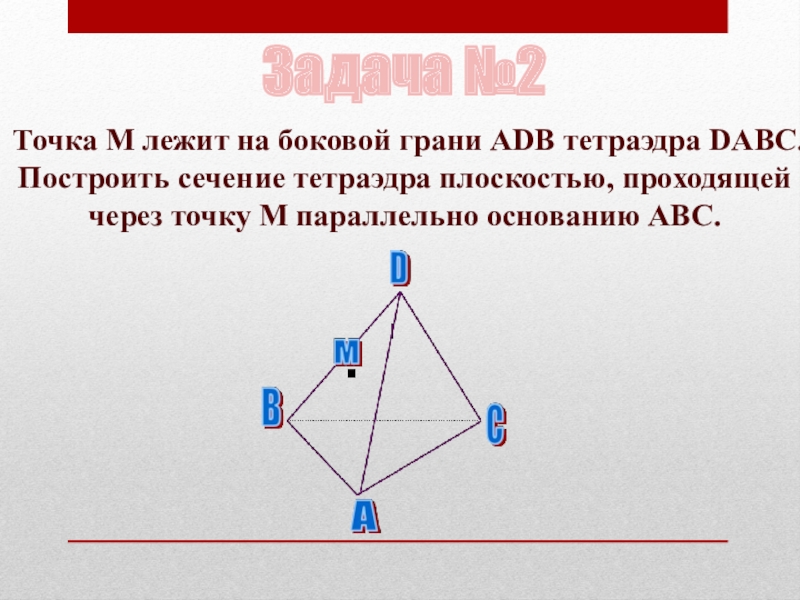
Слайд 56Задача №2
Точка М лежит на боковой грани ADB тетраэдра DABC. Построить
сечение тетраэдра плоскостью, проходящей через точку М параллельно основанию ABC.
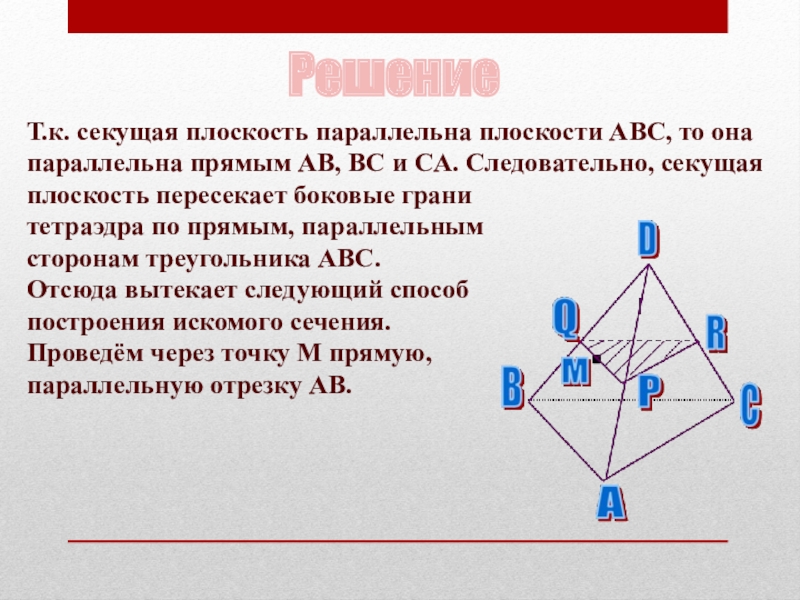
Слайд 57Решение
Т.к. секущая плоскость параллельна плоскости ABC, то она параллельна прямым AB,
BC и CA. Следовательно, секущая плоскость пересекает боковые грани
тетраэдра по прямым, параллельным
сторонам треугольника ABC.
Отсюда вытекает следующий способ построения искомого сечения. Проведём через точку М прямую, параллельную отрезку AB.
Отсюда вытекает следующий способ построения искомого сечения. Проведём через точку М прямую, параллельную отрезку AB.
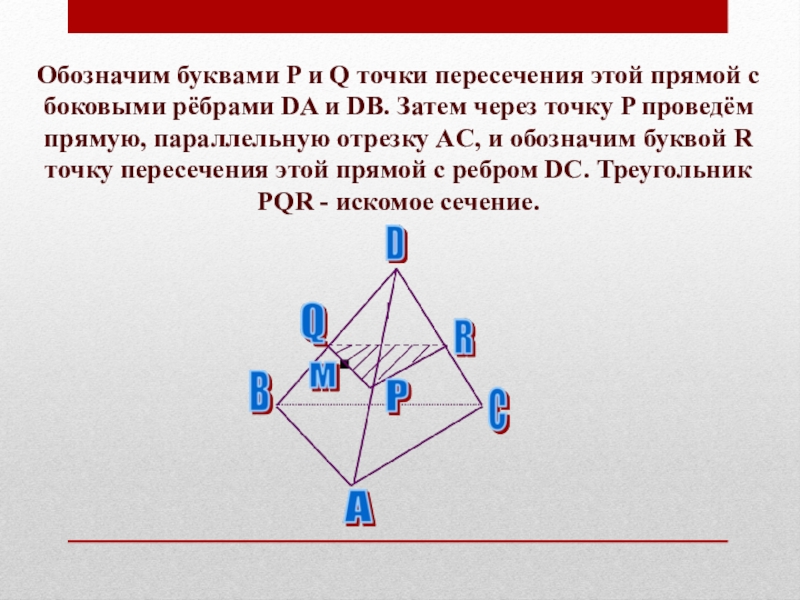
Слайд 58Обозначим буквами P и Q точки пересечения этой прямой с боковыми
рёбрами DA и DB. Затем через точку P проведём прямую, параллельную отрезку AC, и обозначим буквой R точку пересечения этой прямой с ребром DC. Треугольник PQR - искомое сечение.
Слайд 59Задача №3
На рёбрах параллелепипеда даны три точки A, B и C.
Построить сечение параллелепипеда плоскостью ABC.
Слайд 60Решение
Построение искомого сечения зависит от того, на каких рёбрах параллелепипеда лежат
точки A, B и C. Когда эти точки лежат на рёбрах, выходящих из одной вершины, нужно провести отрезки AB, BC и CA, и получится искомое сечение - треугольник ABC.
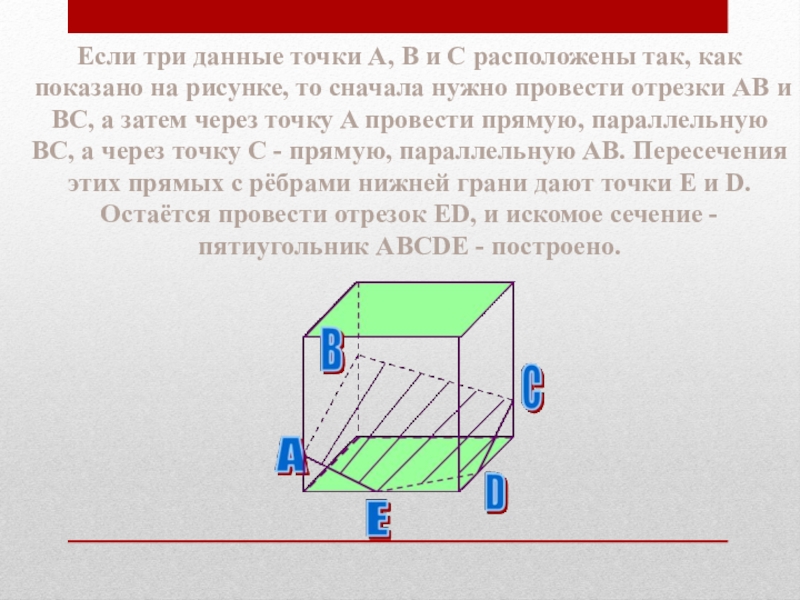
Слайд 61Если три данные точки A, B и C расположены так, как
показано на рисунке, то сначала нужно провести отрезки AB и BC, а затем через точку A провести прямую, параллельную BC, а через точку C - прямую, параллельную AB. Пересечения этих прямых с рёбрами нижней грани дают точки E и D. Остаётся провести отрезок ED, и искомое сечение - пятиугольник ABCDE - построено.
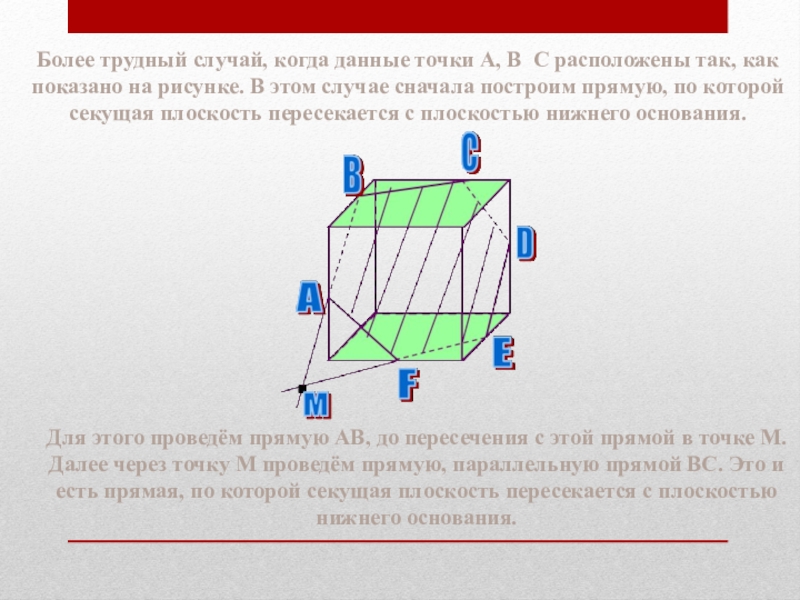
Слайд 62Более трудный случай, когда данные точки A, B C расположены так,
как показано на рисунке. В этом случае сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания.
Для этого проведём прямую AB, до пересечения с этой прямой в точке M. Далее через точку M проведём прямую, параллельную прямой BC. Это и есть прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания.
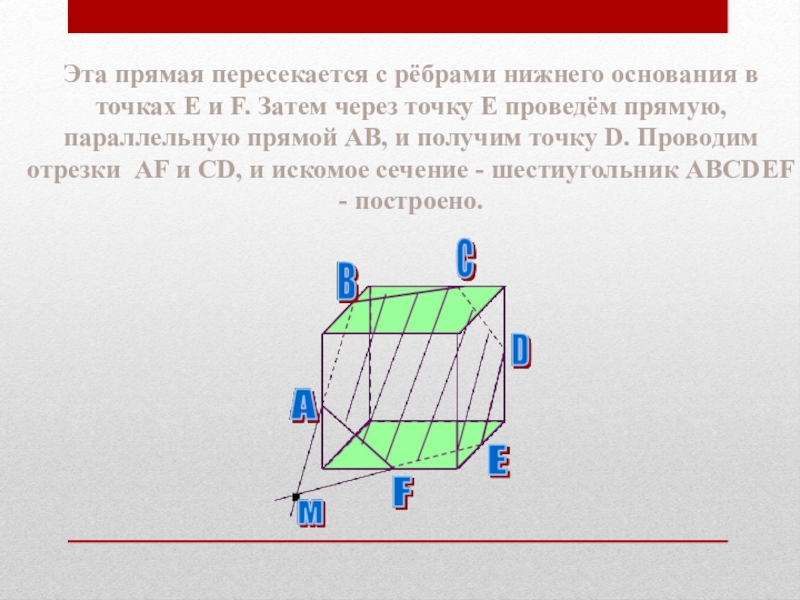
Слайд 63Эта прямая пересекается с рёбрами нижнего основания в точках E и
F. Затем через точку E проведём прямую, параллельную прямой AB, и получим точку D. Проводим отрезки AF и CD, и искомое сечение - шестиугольник ABCDEF - построено.
Слайд 65Задача №1
Построить сечение тетраэдра DABC плоскостью, проходящей через точки M, N,
K. Условие - MN∥AC.
Доказать, что построенное сечение – трапеция.
Доказать, что построенное сечение – трапеция.