- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теорема косинусов. Учебная презентация.
Содержание
- 1. Теорема косинусов. Учебная презентация.
- 2. История возникновения теоремы косинусов.Теорему знали еще древние
- 3. Теорема: квадрат любой стороны треугольника равен сумме
- 4. Доказательство:Дано:∆АВС.Доказать, что ВС2 = АС2 + АВ2
- 5. Следствие из теоремы косинусовНо, доказав теорему, можно
- 6. Рассмотрим треугольник АВС, где А –
- 7. Рассмотрим треугольник АВС, где А –
- 8. Но это – доказательство одного частного случая
- 9. 2) a) По следствию острого угла:а.1) АВ2
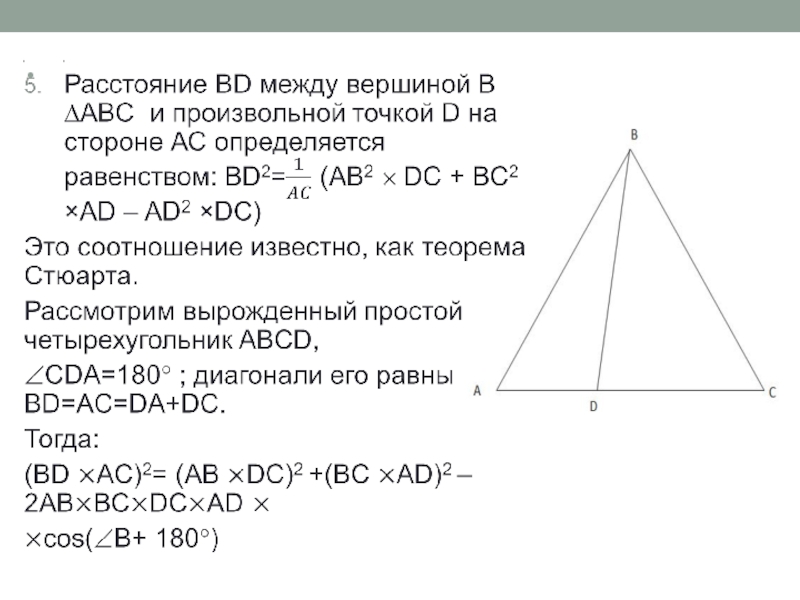
- 10. Две теоремы косинусов для четырехугольника.В практике нередко
- 11. Две теоремы косинусов для четырехугольника.Из всего многообразия
- 12. Теорема 1.Квадрат стороны выпуклого четырехугольника равен сумме
- 13. Доказательство №1:Дано:Треугольник AMDДоказать, что x2 = a2
- 14. Рассмотрим треугольник ECD:по теореме косинусов имеем, чтоy2
- 15. Проведем отрезки ЕЕ1 и DD1. Получим, что
- 16. Внимание: приведенное выше доказательство существенным образом опирается
- 17. Доказательство №2
- 18. Подставим значения e2 и f2 в выражения
- 19. Вторая теорема косинусов для четырехугольника (теорема Бретшнейдера,
- 20. Теорема 2Квадрат произведения диагоналей простого четырехугольника равен
- 21. Дано:φ – угол, φ = A +
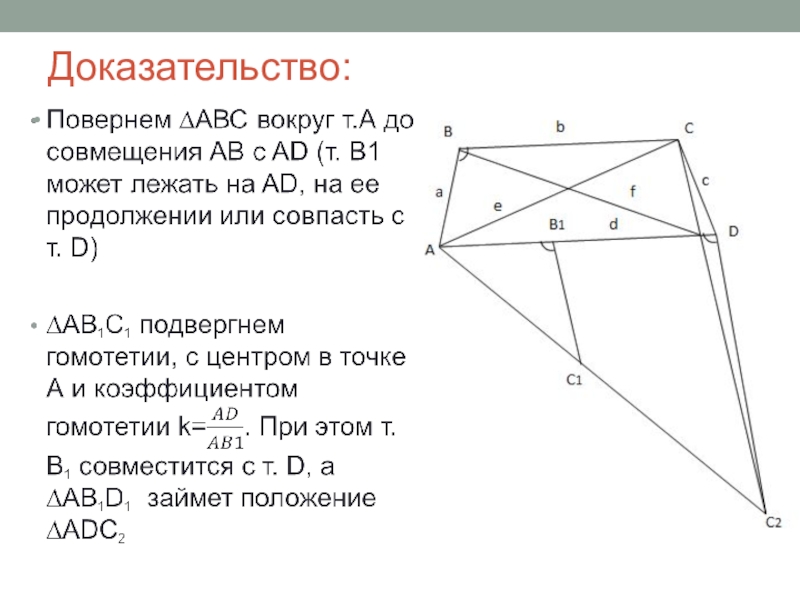
- 22. Доказательство:
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Эта теорема по аналогии с теоремой косинусов
- 27. uВ параллелограмме с острым углом, равным 45,
- 28. Слайд 28
- 29. ЭООВо всяком выпуклом четырехугольнике, вписанном в окружность,
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
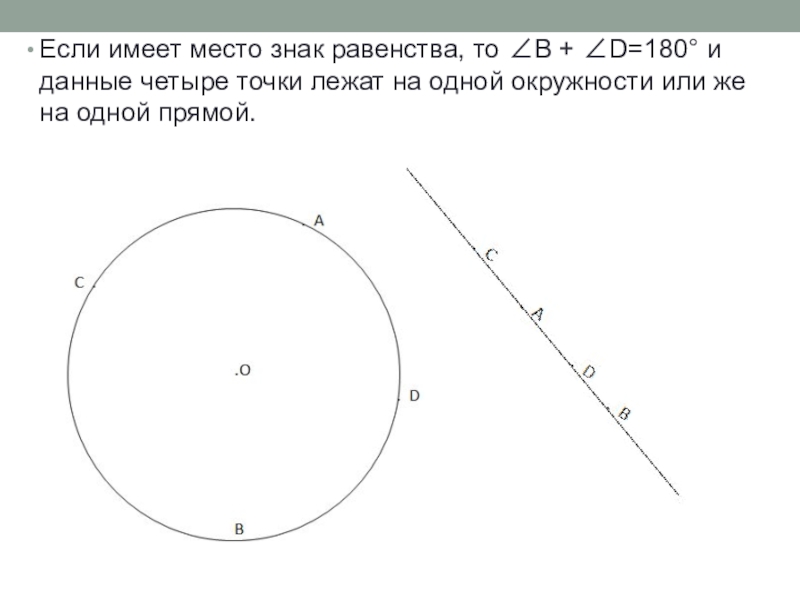
- 33. Если имеет место знак равенства, то B
- 34. Список используемой литературы:З.А. Скопец «Геометрические миниатюры», Москва,
Слайд 1Теорема косинусов
Презентацию подготовили
ученицы 10 класса
МОУ «СОШ № 73»
Джейранова Малах и Львова
Руководитель: Драгунова С.Н.
Слайд 2История возникновения теоремы косинусов.
Теорему знали еще древние греки: ее доказательство содержится
Слайд 3Теорема: квадрат любой стороны треугольника равен сумме квадратов двух других сторон
Слайд 4Доказательство:
Дано:
∆АВС.
Доказать, что ВС2 = АС2 + АВ2 – 2АС × АВ
Доказательство:
Рассмотрим векторное равенство.
Т.к.
то
Возведём обе части в квадрат (скалярно), тогда получим:
Т.к. =│ a│ ×│ b│ × cos (a ; b ), то ВС2 = АС2 + АВ2 – 2АС × АВ × cosA , что и требовалось доказать.
Слайд 5Следствие из теоремы косинусов
Но, доказав теорему, можно выявить следствие: квадрат любой
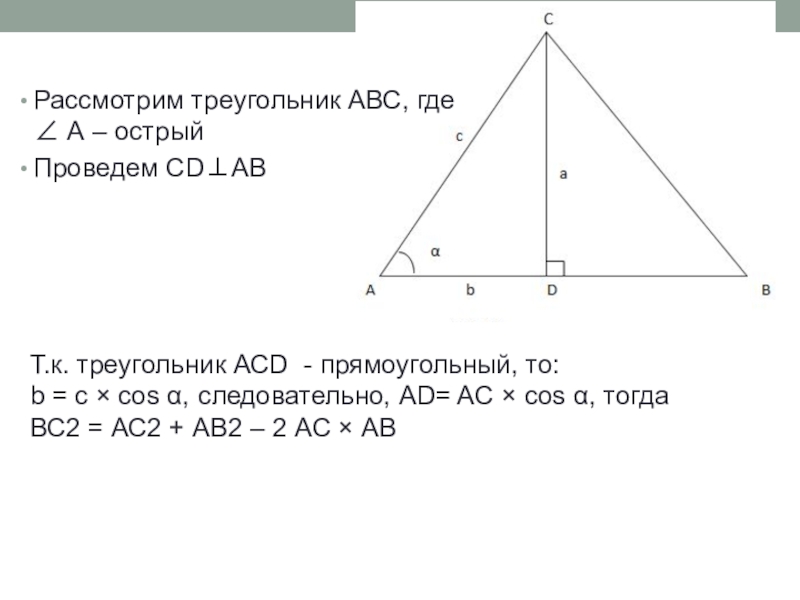
Слайд 6Рассмотрим треугольник АВС, где А – острый
Проведем CDAB
Т.к. треугольник АСD
b = c × cos α, следовательно, AD= AC × cos α, тогда ВС2 = АС2 + АВ2 – 2 АС × АВ
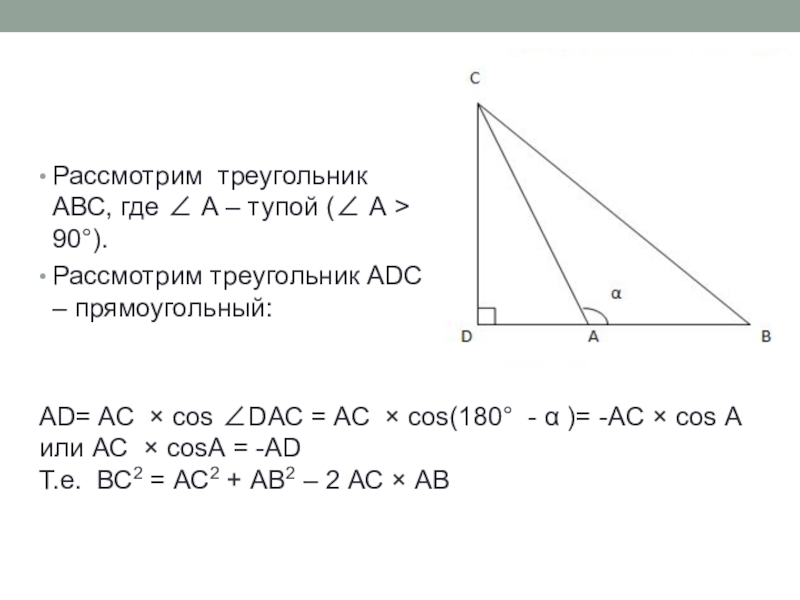
Слайд 7Рассмотрим треугольник АВС, где А – тупой ( А
Рассмотрим треугольник АDС – прямоугольный:
AD= AC × cos DAC = AC × cos(180 - α )= -AC × cos А или AC × cosА = -AD
Т.е. ВС2 = АС2 + АВ2 – 2 АС × АВ
Слайд 8Но это – доказательство одного частного случая теоремы, одной стороны треугольника.
По теореме:
а) АС2 = АВ2 + ВС2 – 2 АВ × ВС × cosВ
б) АВ2 = АС2 + ВС2 – 2 АС × ВС × cosС
в) если один из углов прямой, то имеем треугольник АВС – прямоугольный и стороны вычисляются по теореме Пифагора (a2 + b2 = c2)
Слайд 92) a) По следствию острого угла:
а.1) АВ2 = АС2 + ВС2
а.2) АС2= АВ2 + ВС2 - 2 ВС × СD
б) По следствию тупого угла:
б.1) АВ2 = АС2 + ВС2 + 2 АD × ВС
б.2) АС2= АВ2 + ВС2 + 2 ВС × СD
Слайд 10Две теоремы косинусов для четырехугольника.
В практике нередко возникают задачи, решение которых
Так, в геодезии приходится иметь дело с выяснением взаимного расположения четырех пунктов, в технике – с расчетами четырёхзвёздных шарнирных механизмов и т.п.
Слайд 11Две теоремы косинусов для четырехугольника.
Из всего многообразия возникающих здесь вопросов нами
Слайд 12Теорема 1.
Квадрат стороны выпуклого четырехугольника равен сумме квадратов трех других сторон
Слайд 13Доказательство №1:
Дано:
Треугольник AMD
Доказать, что x2 = a2 + b2 + c2
Доказательство.
Построим ABCE – параллелограмм
Имеем: ECD =AMD =μ
Пусть CE=a, AE=b, ED=y, AD=x
ABC=β, BCD=γ, AED=φ
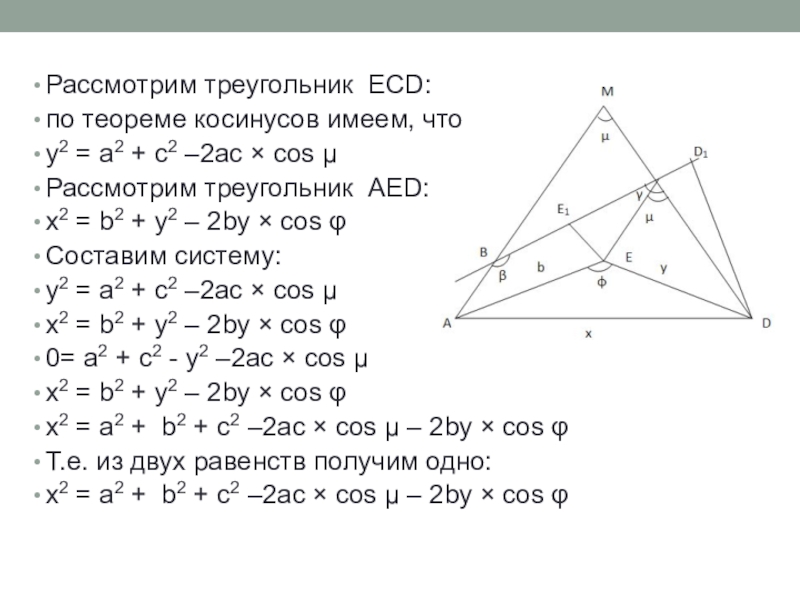
Слайд 14Рассмотрим треугольник ECD:
по теореме косинусов имеем, что
y2 = a2 + c2
Рассмотрим треугольник AED:
x2 = b2 + y2 – 2by × cos φ
Составим систему:
y2 = a2 + c2 –2ac × cos μ
x2 = b2 + y2 – 2by × cos φ
0= a2 + c2 - y2 –2ac × cos μ
x2 = b2 + y2 – 2by × cos φ
x2 = a2 + b2 + c2 –2ac × cos μ – 2by × cos φ
Т.е. из двух равенств получим одно:
x2 = a2 + b2 + c2 –2ac × cos μ – 2by × cos φ
Слайд 15Проведем отрезки ЕЕ1 и DD1. Получим, что
y= cos ( 180
Подставим найденное значение y × cos φ в выражение для x2, получим окончательно:
x2 = a2 + b2 + c2 – 2ab × cosβ – 2bc × cos γ – 2ac × cos μ
Теорема доказана.
Слайд 16Внимание: приведенное выше доказательство существенным образом опирается на чертеж. Необходимо рассмотреть
Приведем второе доказательство, которое не нуждается в рассмотрении различных случаев расположения элементов четырехугольника.
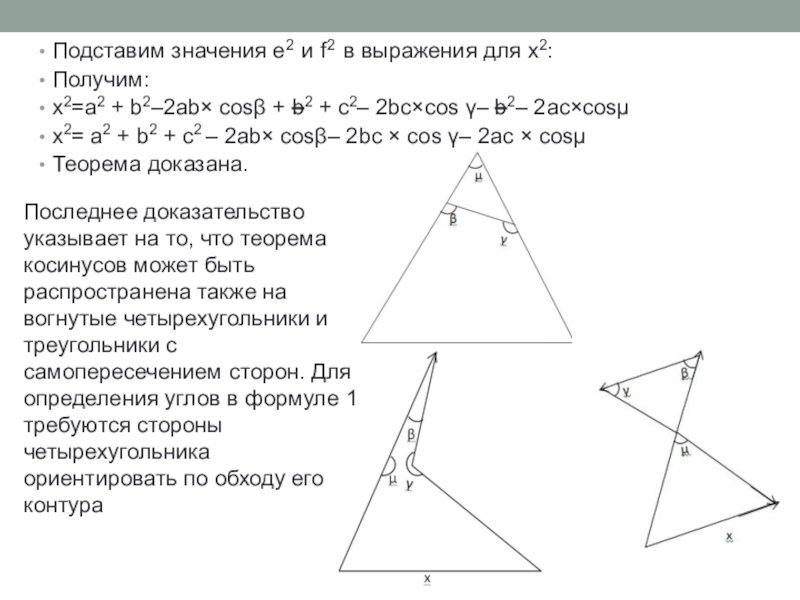
Слайд 18Подставим значения e2 и f2 в выражения для x2:
Получим:
x2=a2 + b2–2ab×
x2= a2 + b2 + c2 – 2ab× cosβ– 2bc × cos γ– 2ac × cosμ
Теорема доказана.
Последнее доказательство указывает на то, что теорема косинусов может быть распространена также на вогнутые четырехугольники и треугольники с самопересечением сторон. Для определения углов в формуле 1 требуются стороны четырехугольника ориентировать по обходу его контура
Слайд 19Вторая теорема косинусов для четырехугольника (теорема Бретшнейдера, 1843 г), насколько известно,
Слайд 20Теорема 2
Квадрат произведения диагоналей простого четырехугольника равен сумме квадратов произведений его
Эта теорема названа теоремой косинусов для четырехугольника потому, что она аналогична теореме косинусов для треугольника, стороны которого пропорциональны произведениям ef, aс, bd, где a, b, c, d – последовательные стороны данного четырехугольника, e и f – его диагонали. Существование такого треугольника легко может быть установлено.
Слайд 21Дано:
φ – угол, φ = A + C или B +D
ABCD
a, b, c, d – стороны, e и f –диагонали
Доказать, что e2f2=a2c2 +b2d2 – 2abcd× cos φ
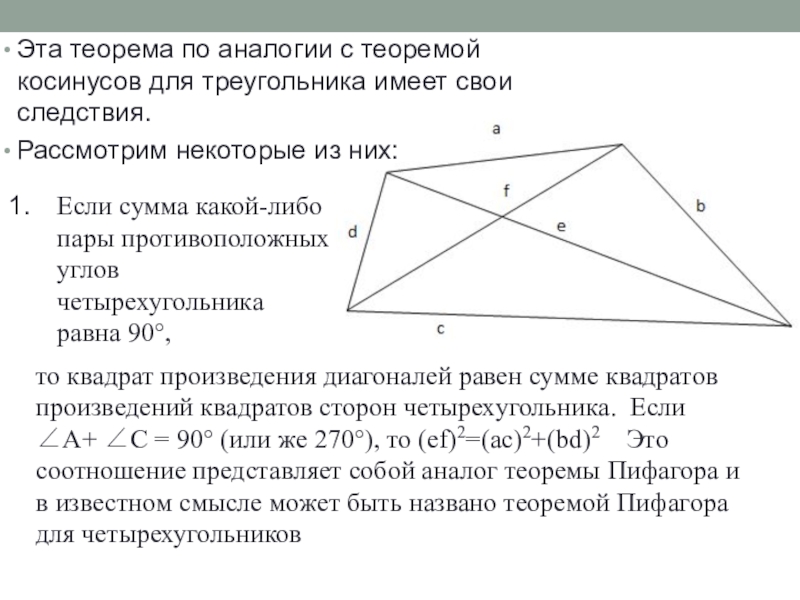
Слайд 26Эта теорема по аналогии с теоремой косинусов для треугольника имеет свои
Рассмотрим некоторые из них:
Если сумма какой-либо пары противоположных углов четырехугольника равна 90,
то квадрат произведения диагоналей равен сумме квадратов произведений квадратов сторон четырехугольника. Если А+ С = 90 (или же 270), то (ef)2=(ac)2+(bd)2 Это соотношение представляет собой аналог теоремы Пифагора и в известном смысле может быть названо теоремой Пифагора для четырехугольников
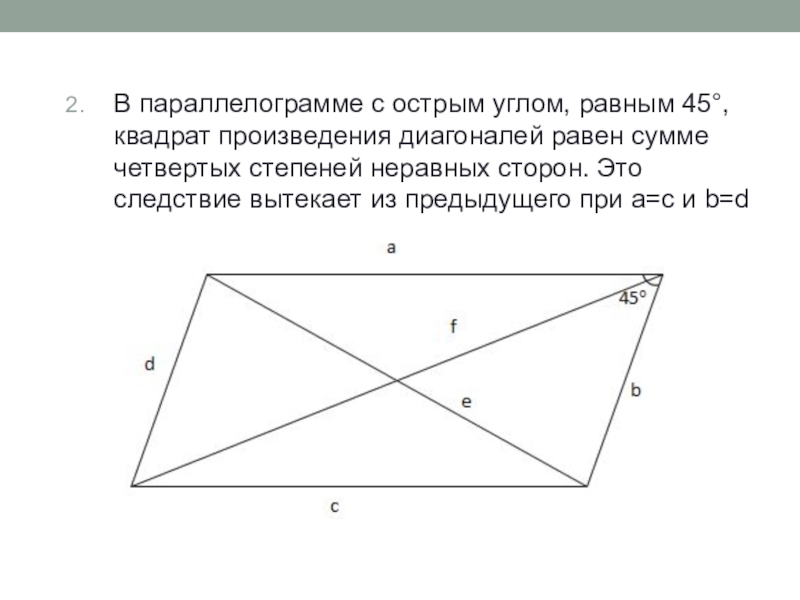
Слайд 27u
В параллелограмме с острым углом, равным 45, квадрат произведения диагоналей равен
Слайд 29Э
О
О
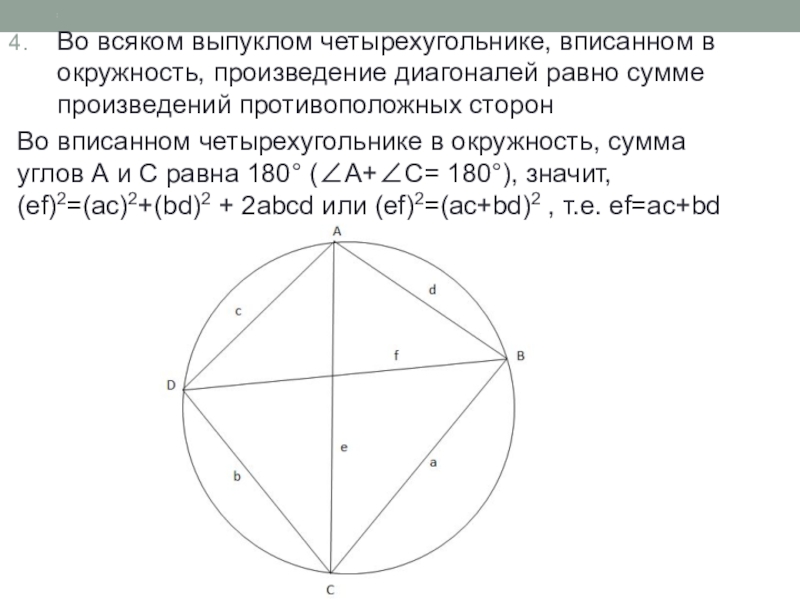
Во всяком выпуклом четырехугольнике, вписанном в окружность, произведение диагоналей равно сумме
Во вписанном четырехугольнике в окружность, сумма углов А и С равна 180 (A+С= 180), значит, (ef)2=(ac)2+(bd)2 + 2abcd или (ef)2=(ac+bd)2 , т.е. ef=ac+bd
Слайд 33Если имеет место знак равенства, то B + D=180 и данные
Слайд 34Список используемой литературы:
З.А. Скопец «Геометрические миниатюры», Москва, 1990 г.
И.Ф. Шарынин «Геометрия.
М.И. Сканави и др. «Сборник конкурсных задач по математике для поступающих во ВТУЗы» Москва, 1978
А.В. Погорелов. «Геометрия 7-11» Москва, 1996
«Энциклопедический словарь юного математика» Москва, 1989