- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тема Площадь на экзаменах в форме ОГЭ
Содержание
- 1. Тема Площадь на экзаменах в форме ОГЭ
- 2. Устная работа по заданиям ЕГЭ
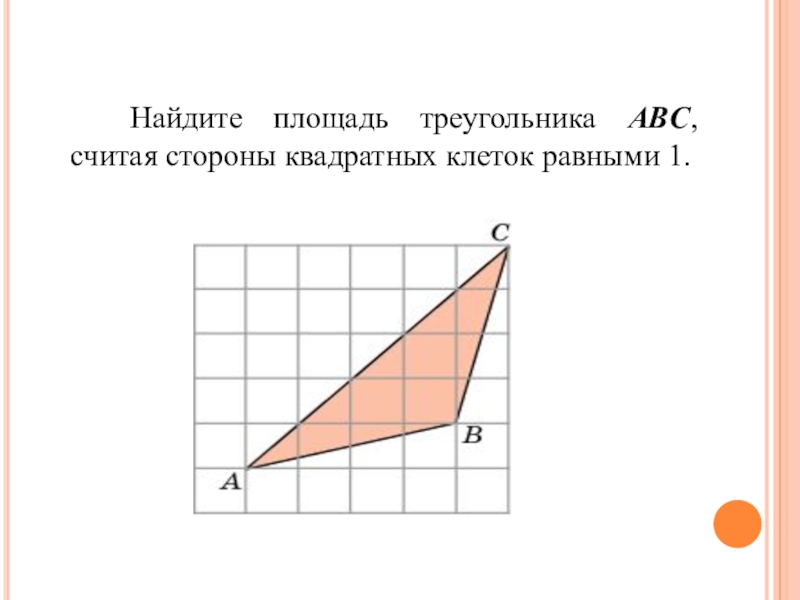
- 3. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
- 4. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
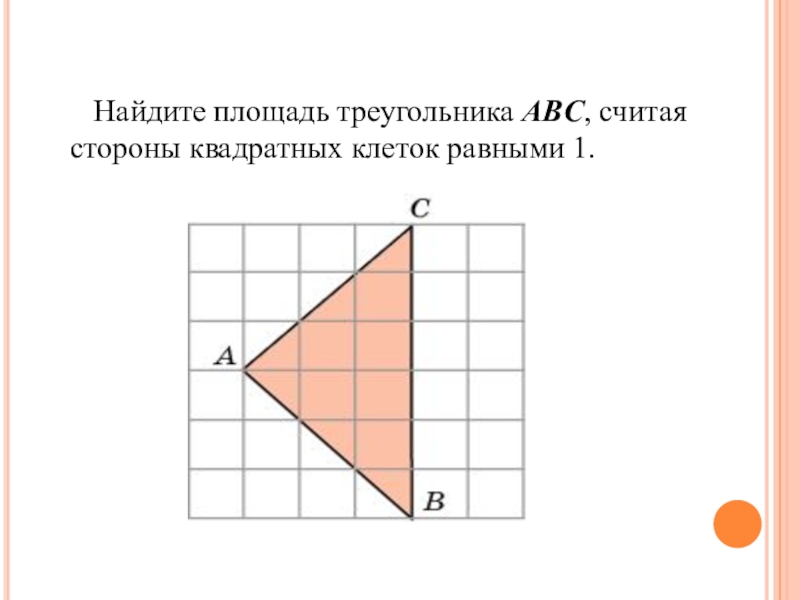
- 5. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
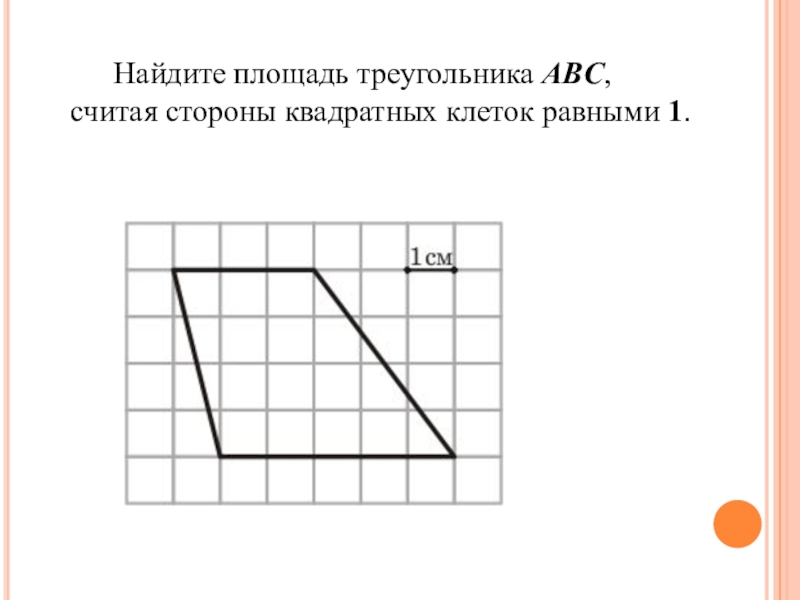
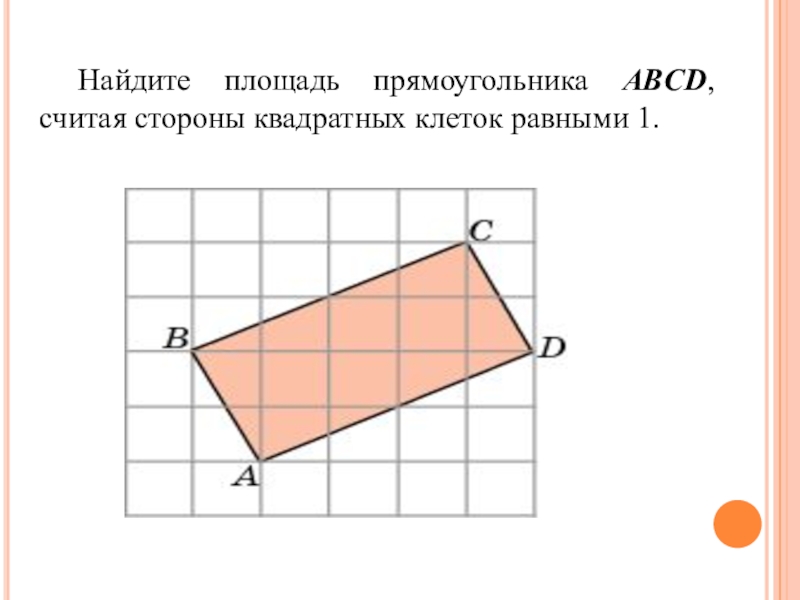
- 6. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
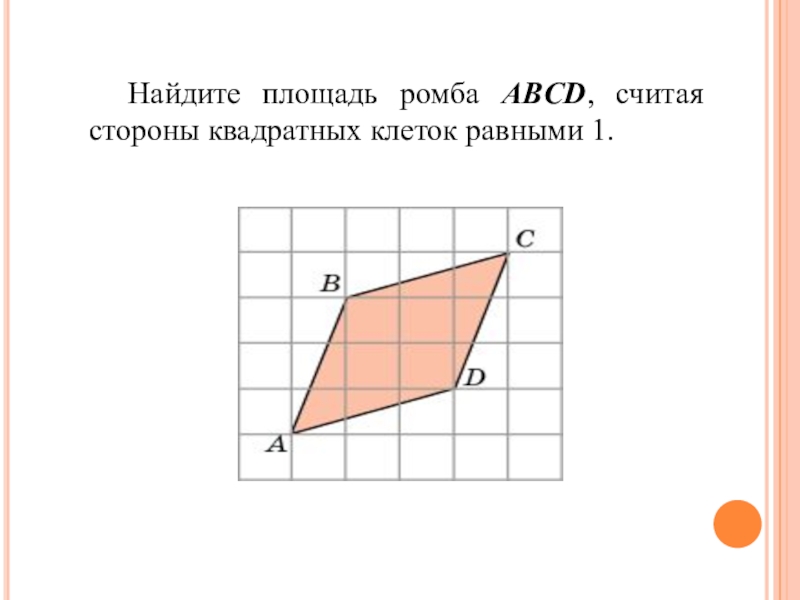
- 7. Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1.
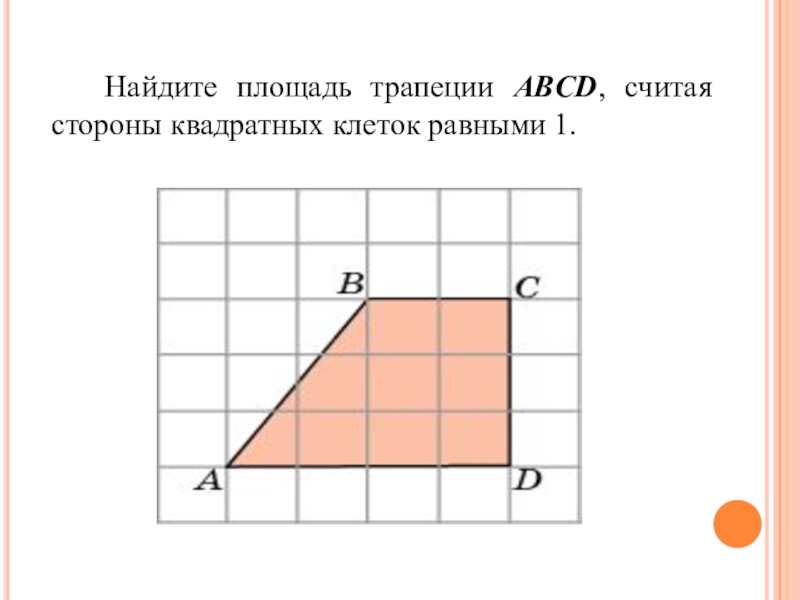
- 8. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
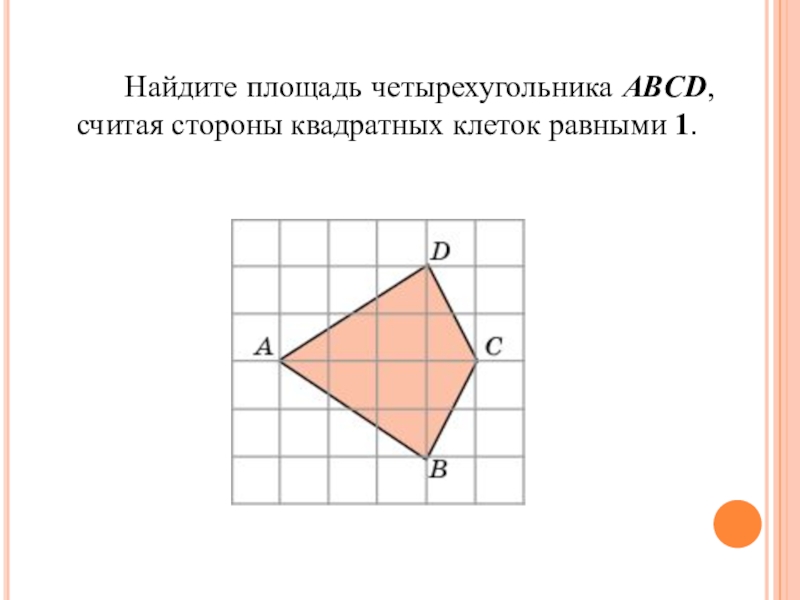
- 9. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
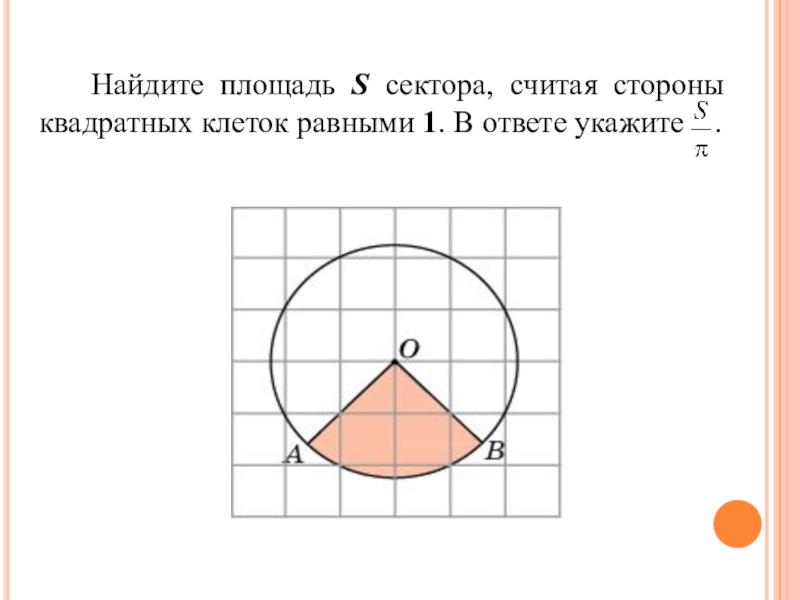
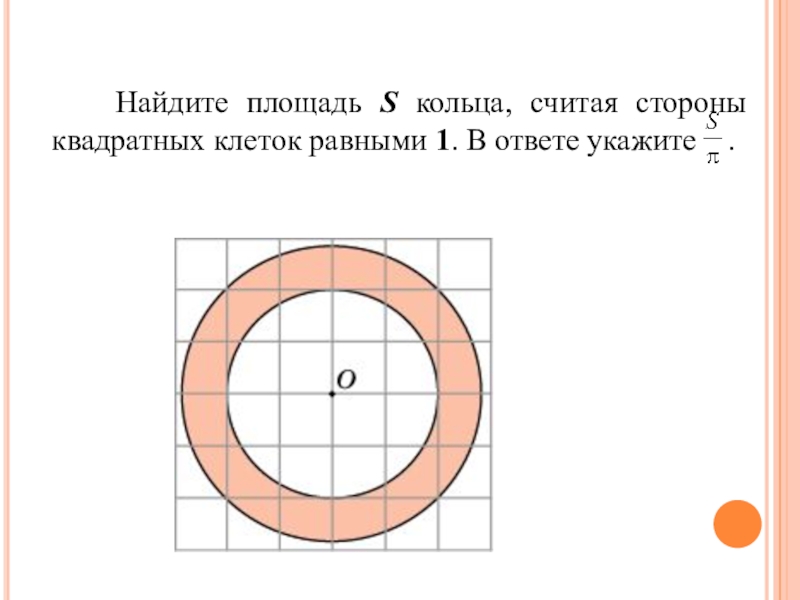
- 10. Найдите площадь S сектора, считая стороны
- 11. Найдите площадь
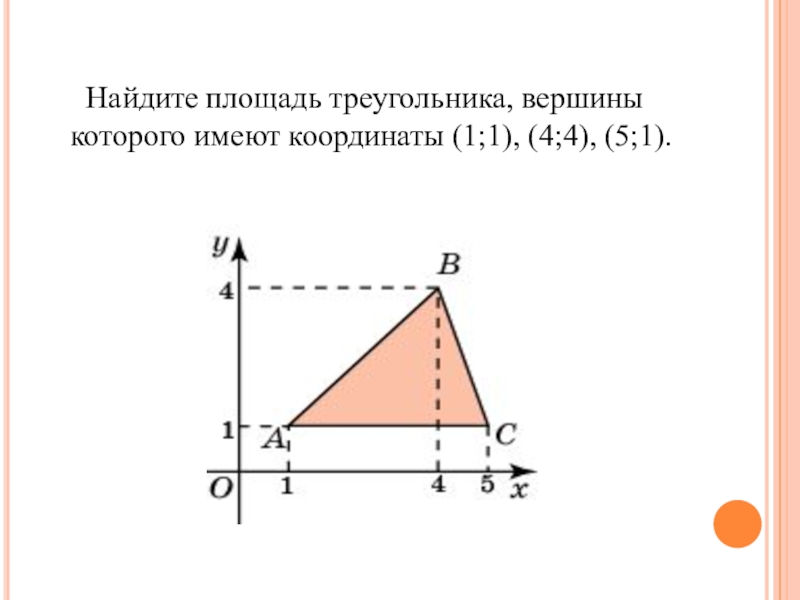
- 12. Найдите площадь треугольника, вершины которого имеют координаты (1;1), (4;4), (5;1).
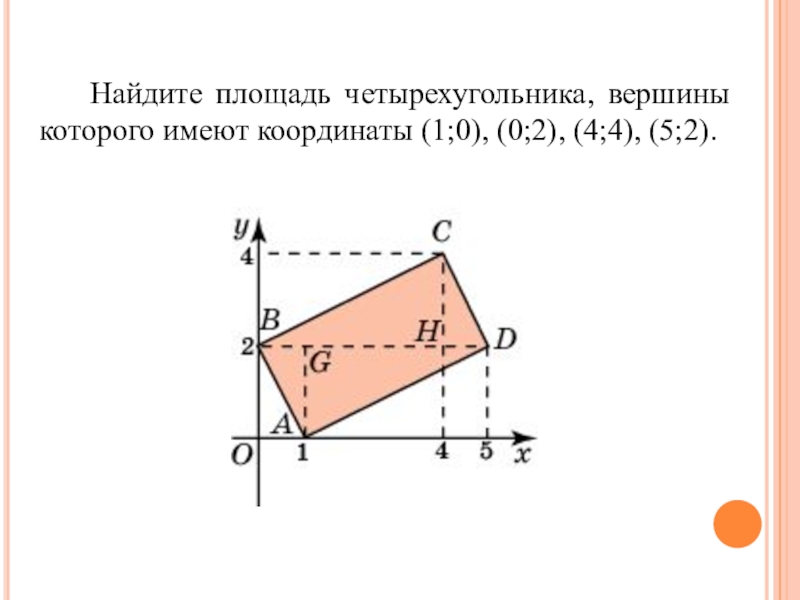
- 13. Найдите площадь четырехугольника, вершины которого имеют координаты (1;0), (0;2), (4;4), (5;2).
- 14. Основные свойства площадей и их применение
- 15. Слайд 15
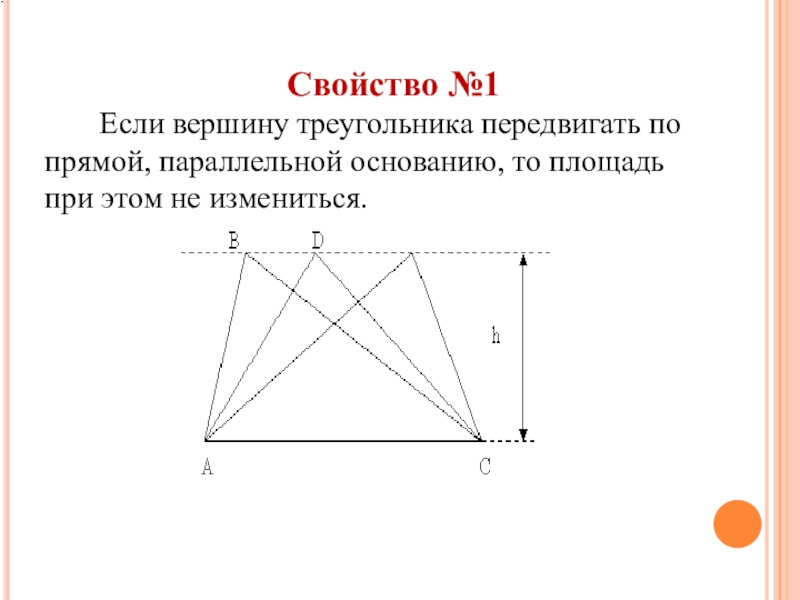
- 16. Свойство №1 Если вершину
- 17. Свойство №2 Если два
- 18. Свойство №3 Если два
- 19. Свойство №4 Отношение площадей подобных треугольников равны квадрату коэффициента подобия. S/S₁= k²
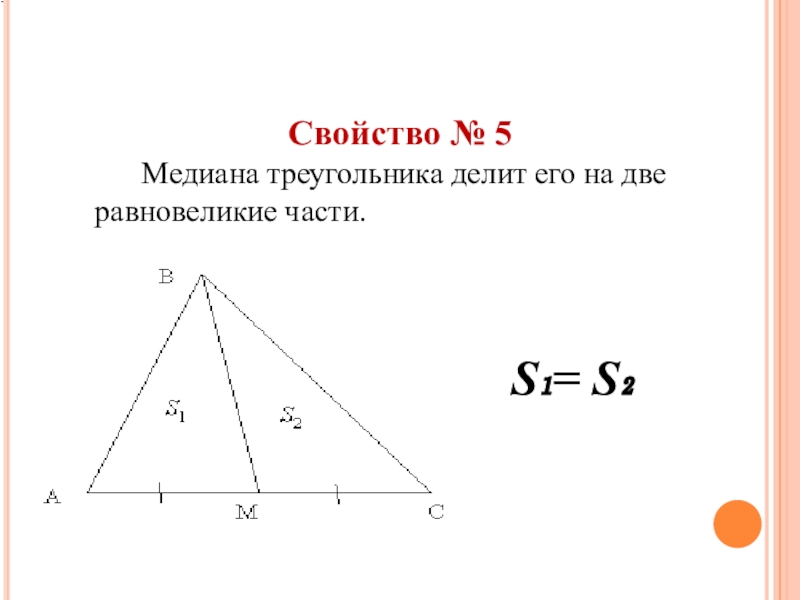
- 20. Свойство № 5 Медиана треугольника
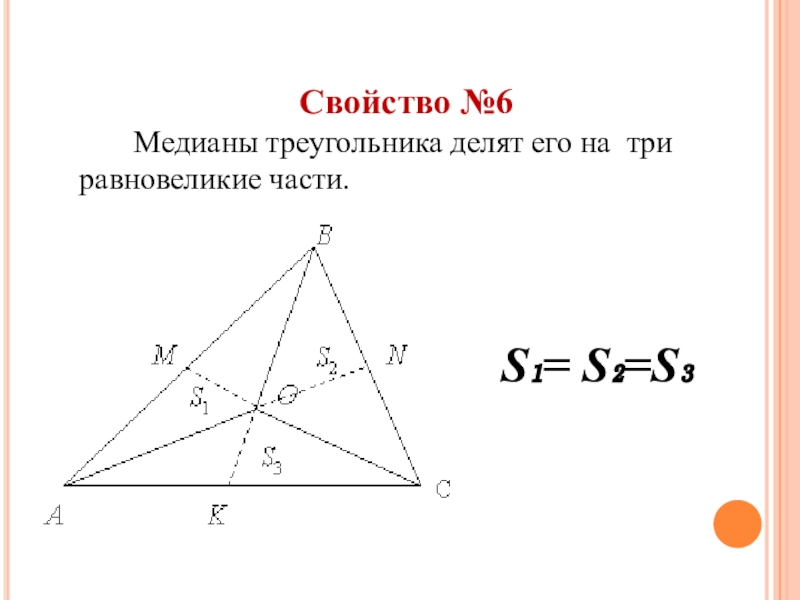
- 21. Свойство №6 Медианы
- 22. Свойство №7 Средние линии
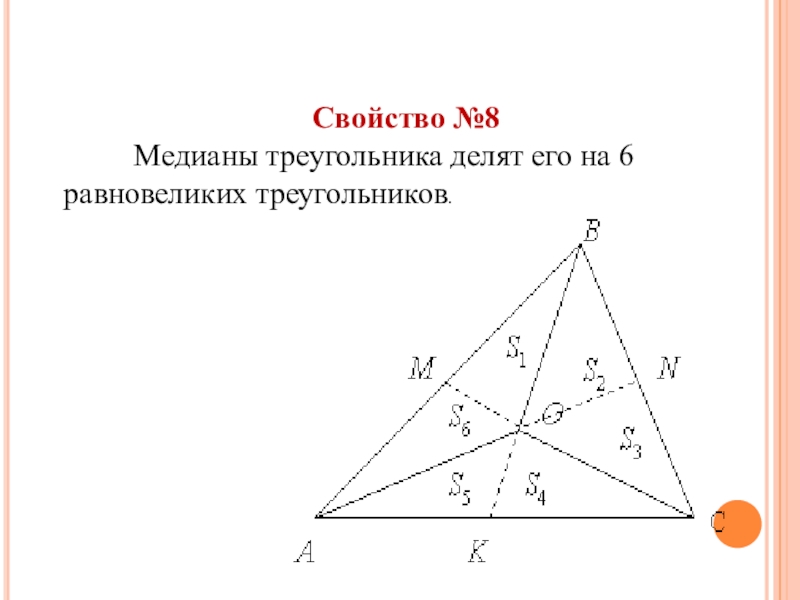
- 23. Свойство №8 Медианы треугольника делят его на 6 равновеликих треугольников.
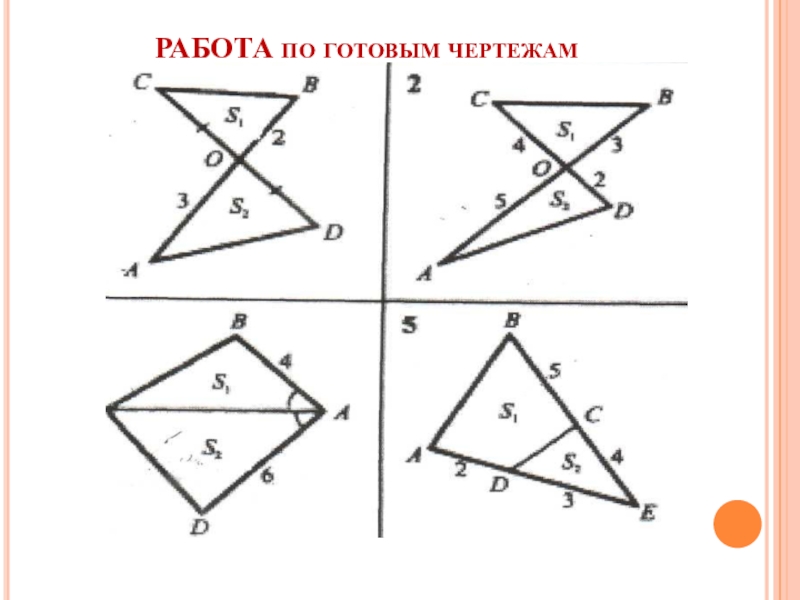
- 24. РАБОТА по готовым чертежам
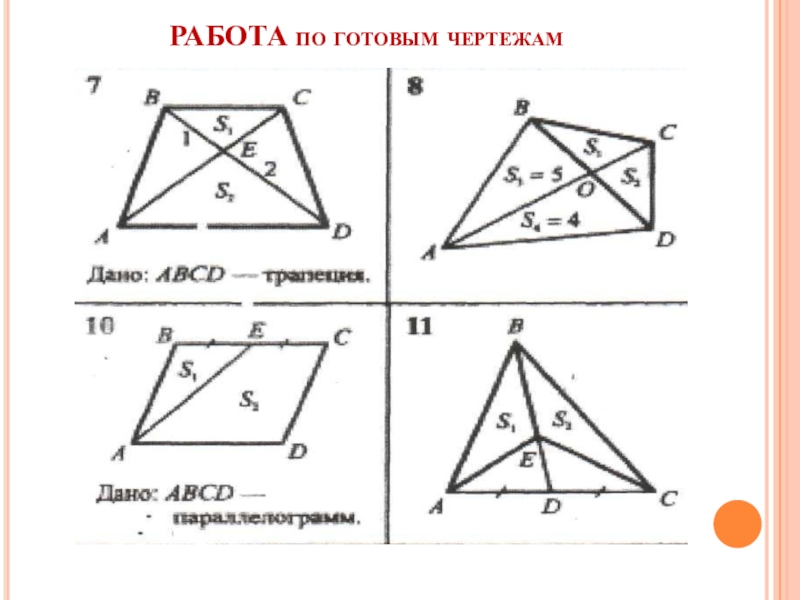
- 25. РАБОТА по готовым чертежам
- 26. Различные задания по теме: «Площадь»
- 27. Задача №1А
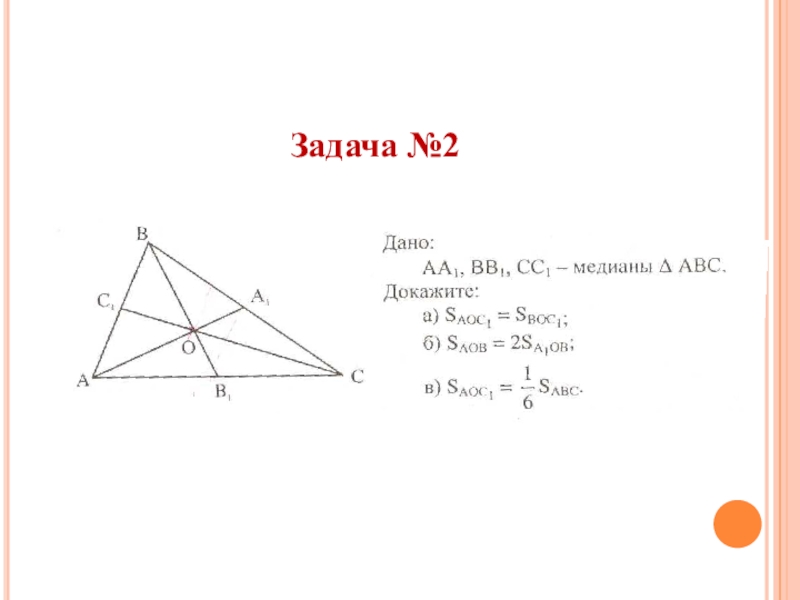
- 28. Задача №2
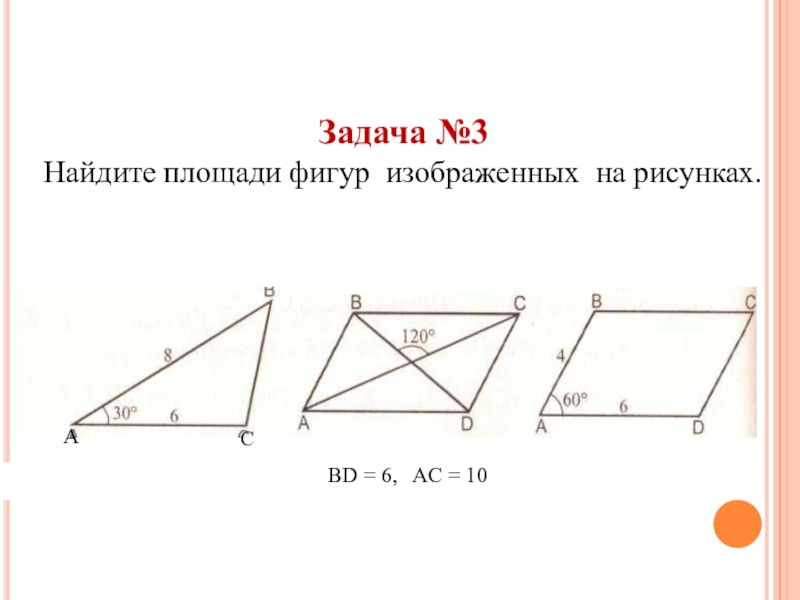
- 29. Задача №3Найдите площади фигур изображенных на рисунках.BD = 6, AC = 10АС
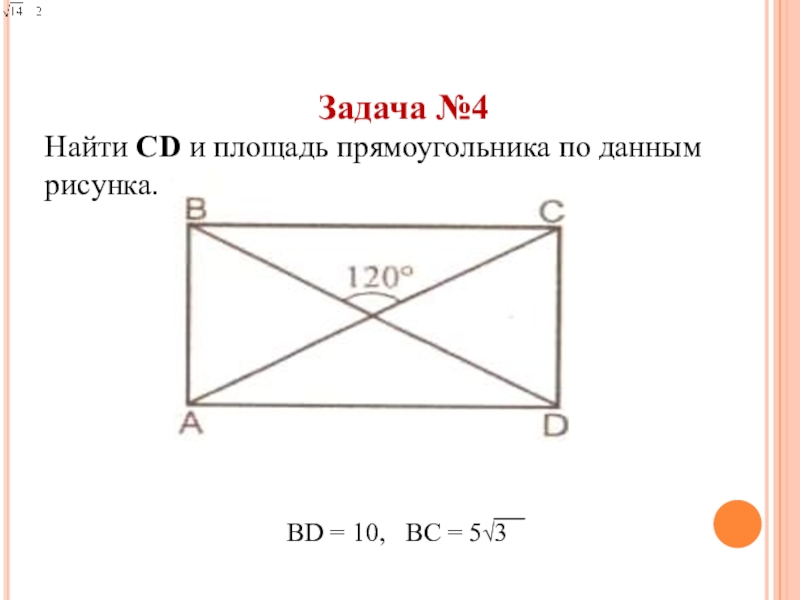
- 30. Задача №4Найти СD и площадь прямоугольника по данным рисунка.BD = 10, ВC = 5√3
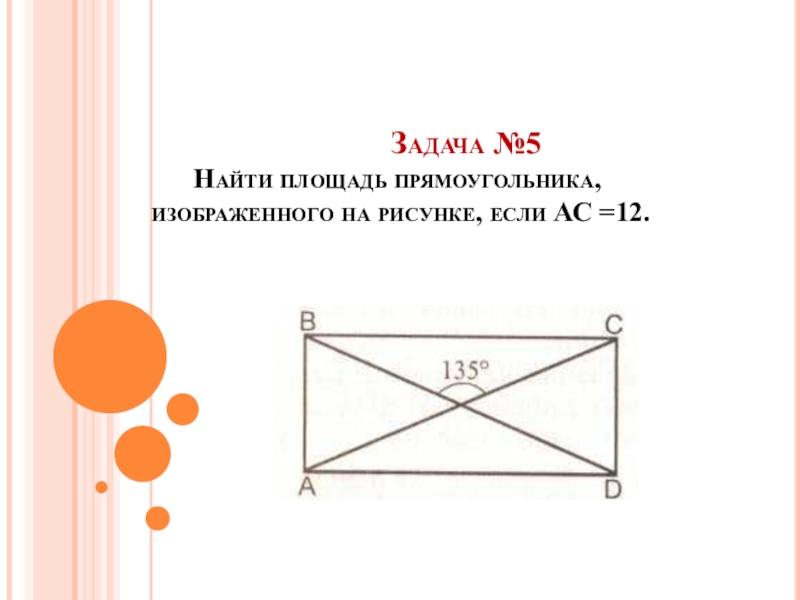
- 31. Слайд 31
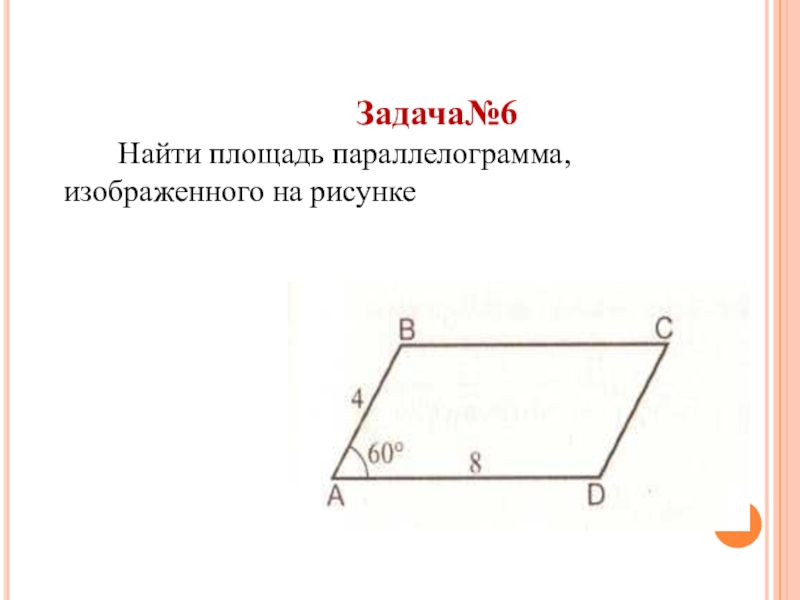
- 32. Задача№6 Найти площадь параллелограмма, изображенного на рисунке
- 33. Слайд 33
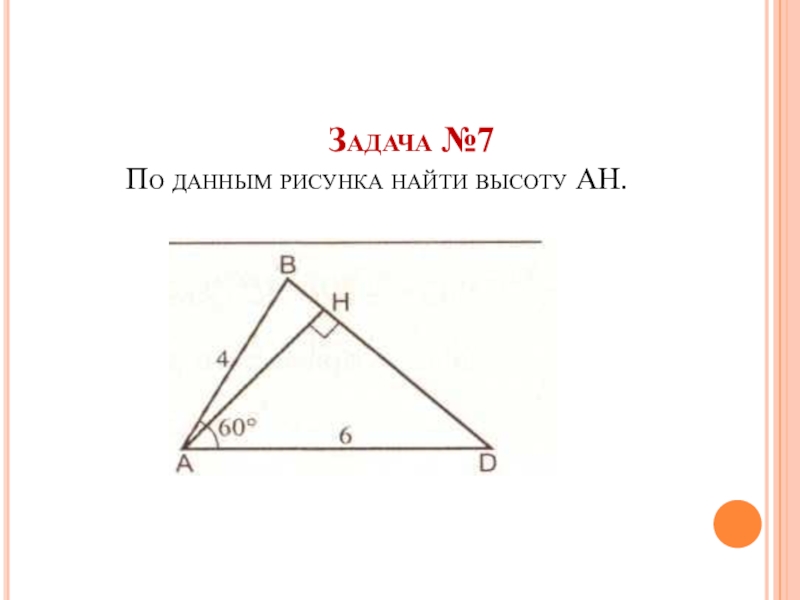
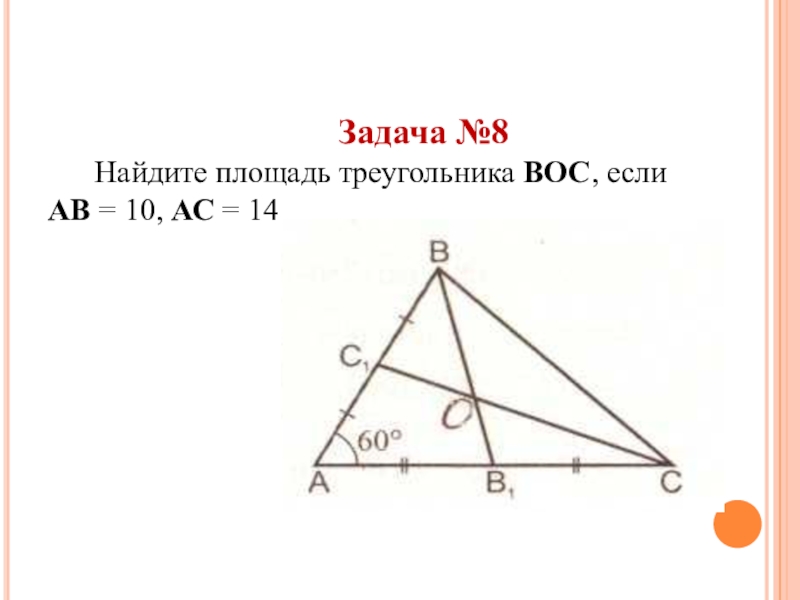
- 34. Задача №8
- 35. Задания первой части ОГЭ
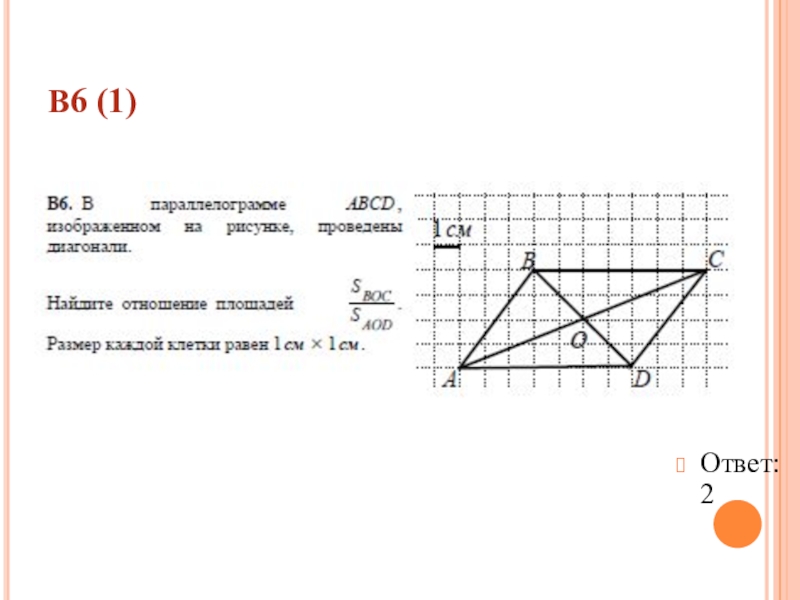
- 36. В6 (1)Ответ: 2
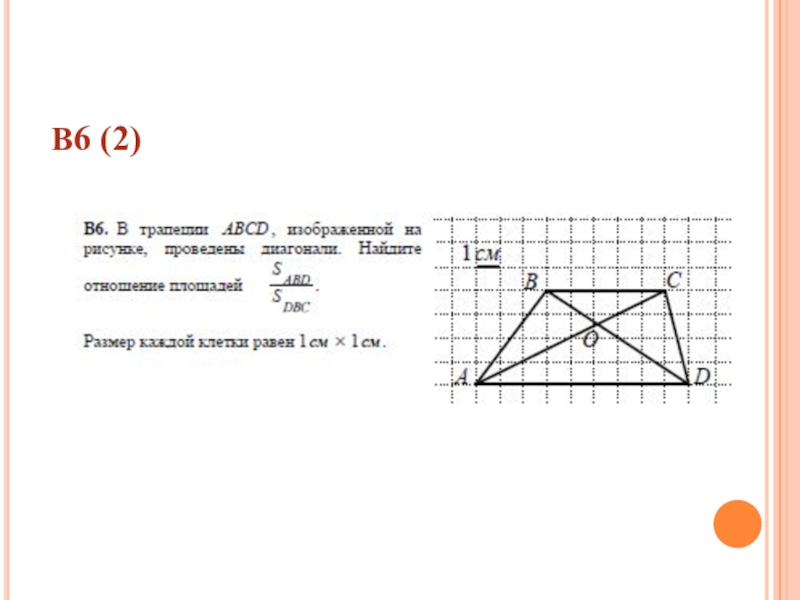
- 37. В6 (2)
- 38. В6 (2)
- 39. Слайд 39
- 40. Задача №2 Найдите площадь трапеции, изображенной на рисунке.Ответ: 69
- 41. Слайд 41
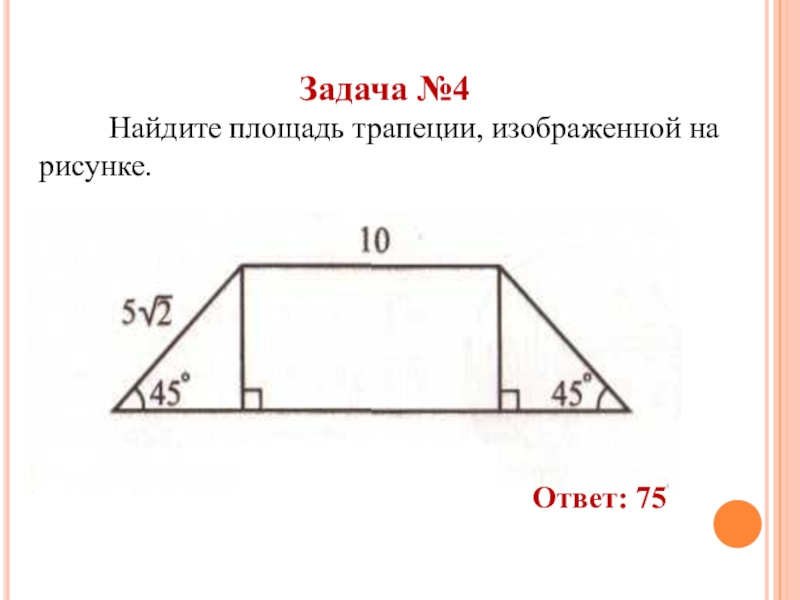
- 42. Задача №4 Найдите площадь трапеции, изображенной на рисунке.Ответ: 75
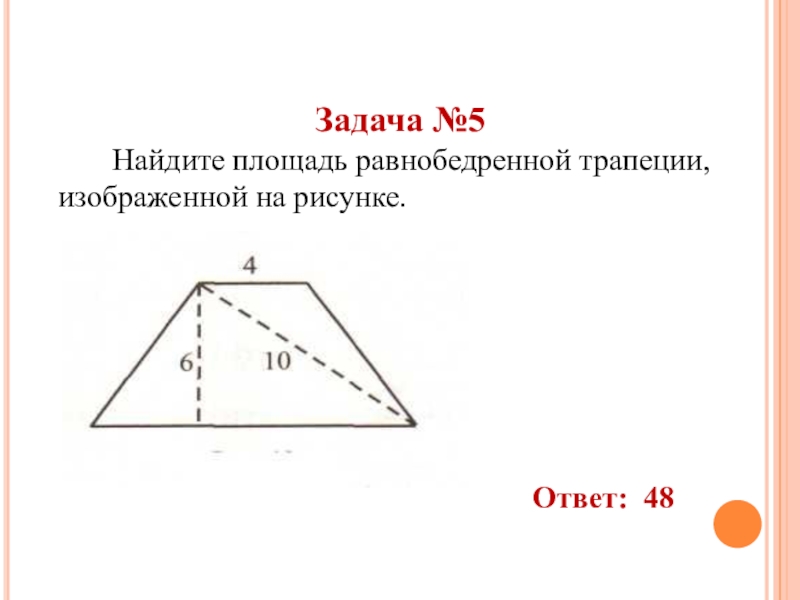
- 43. Задача №5 Найдите площадь равнобедренной трапеции, изображенной на рисунке.Ответ: 48
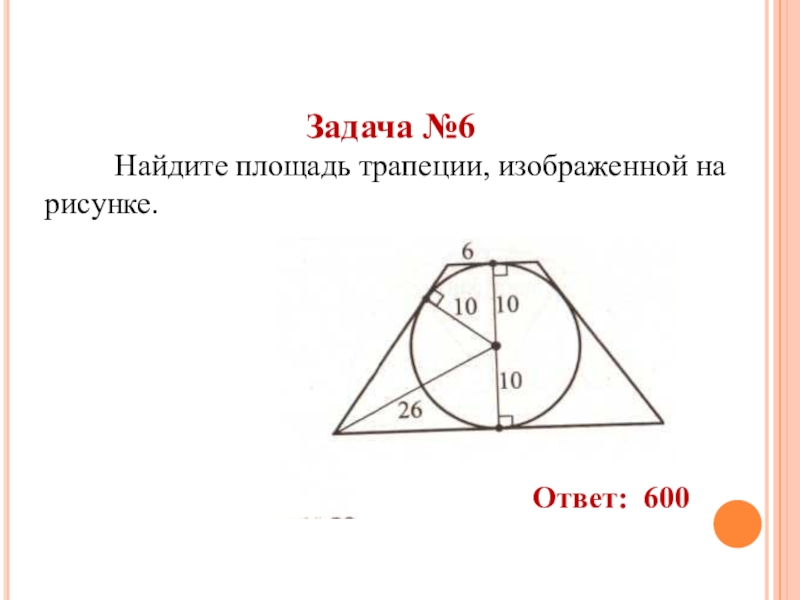
- 44. Задача №6 Найдите площадь трапеции, изображенной на рисунке.Ответ: 600
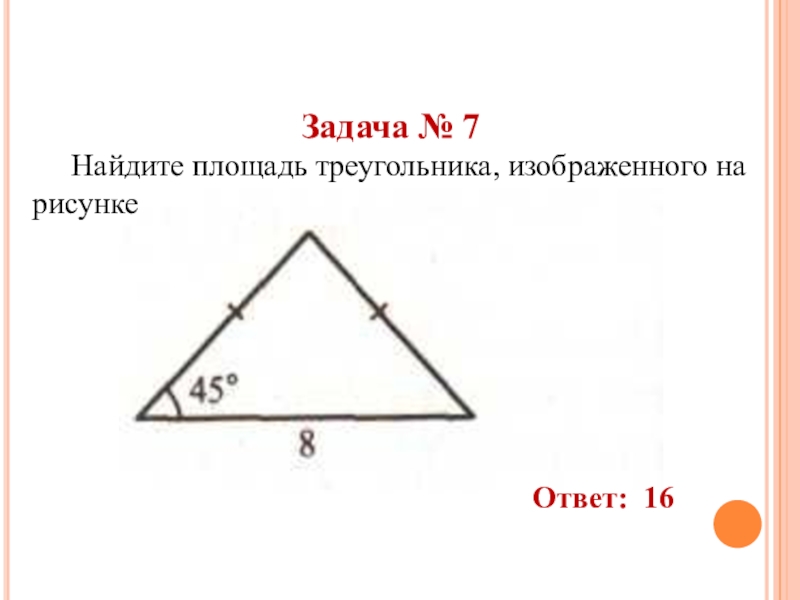
- 45. Задача № 7 Найдите площадь треугольника, изображенного на рисункеОтвет: 16
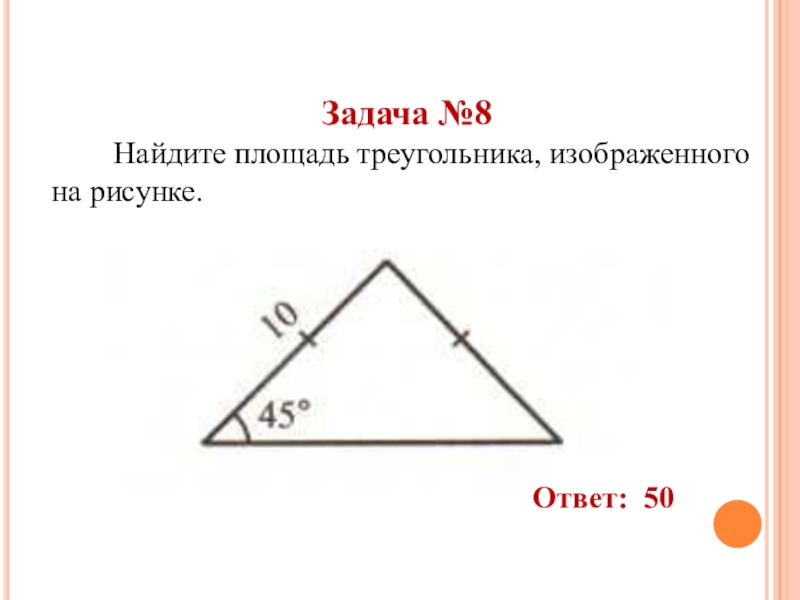
- 46. Задача №8 Найдите площадь треугольника, изображенного на рисунке.Ответ: 50
- 47. Задания второй части ОГЭ
- 48. Слайд 48
- 49. Слайд 49
- 50. № 23 Диагонали
- 51. Слайд 51
- 52. № 26 (1)
- 53. №26 (2)
- 54. №26 (3)
- 55. Слайд 55
- 56. №26 (4)
- 57. Слайд 57
- 58. №26 (5) Площадь
- 59. Слайд 59
Устная работа по заданиям ЕГЭ
Слайд 13 Найдите площадь четырехугольника, вершины которого имеют координаты (1;0), (0;2), (4;4),
(5;2).
Слайд 15
В элементарной математике, самыми
трудными считаются геометрические задачи. Как научиться решать геометрические задачи, особенно сложные, конкурсные? При решении геометрических задач, как правило, алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не просто. Поэтому, желательно в каждой теме выработать какие-то общие положения, которые полезно знать всякому решающему геометрические задачи.
Предлагаем один из алгоритмов решения многих геометрических задач – метод площадей, т.е. решение задач с использованием свойств площадей.
Слайд 16Свойство №1
Если вершину треугольника передвигать по прямой,
параллельной основанию, то площадь
при этом не измениться.
при этом не измениться.
Слайд 17
Свойство №2
Если два треугольника имеют одинаковые высоты,
то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
S1 /S2 = а/b
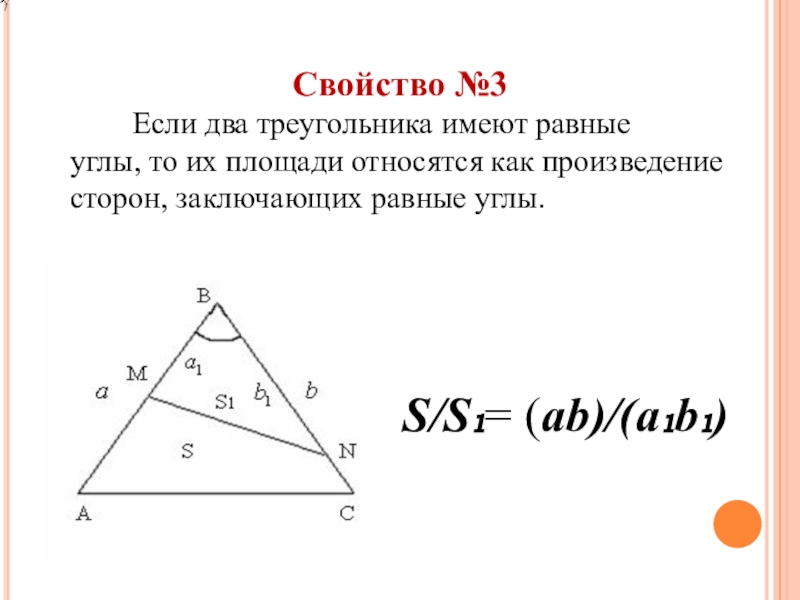
Слайд 18Свойство №3
Если два треугольника имеют равные
углы,
то их площади относятся как произведение сторон, заключающих равные углы.
S/S₁= (ab)/(a₁b₁)
Слайд 19Свойство №4
Отношение площадей подобных треугольников равны квадрату
коэффициента подобия.
S/S₁= k²
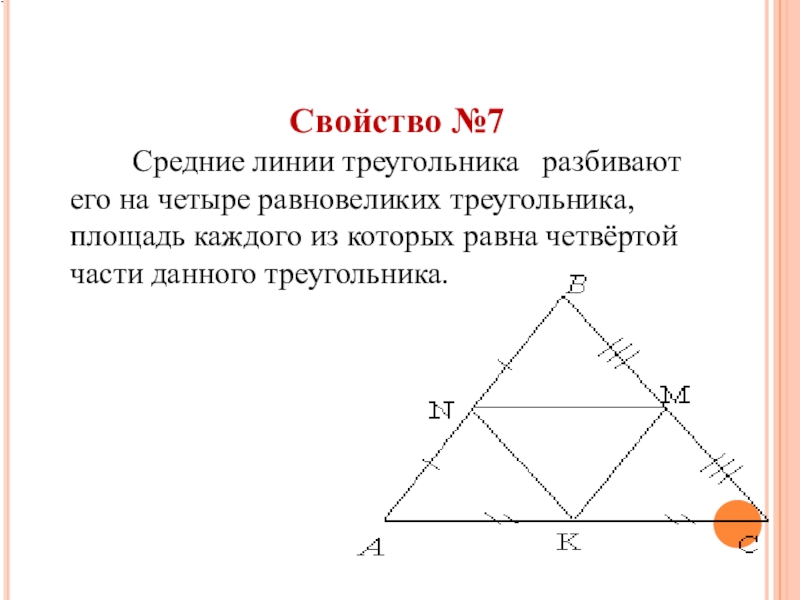
Слайд 22Свойство №7
Средние линии треугольника разбивают его
на четыре равновеликих треугольника, площадь каждого из которых равна четвёртой части данного треугольника.
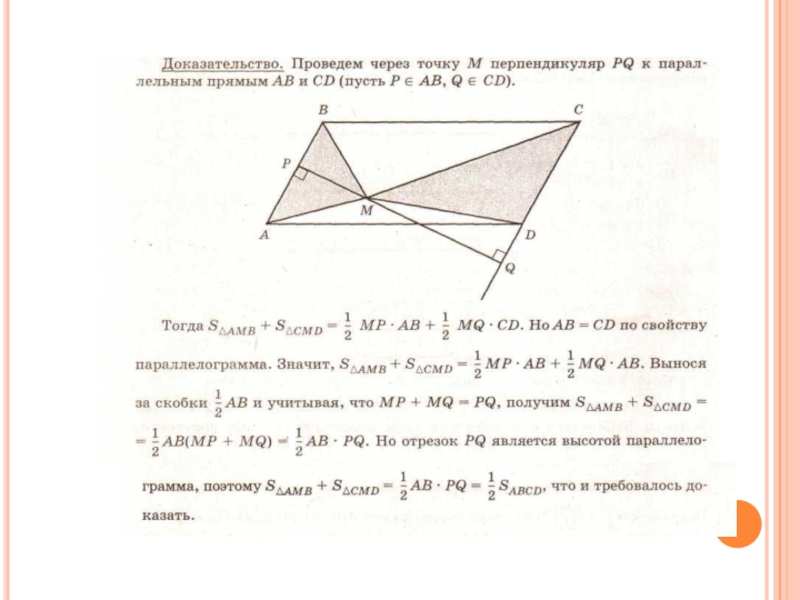
Слайд 50
№ 23
Диагонали АС и ВD трапеции
АВСD пересекаются в точке О.
Площади треугольников АОD и ВОС равны соответственно 25 квадратных сантиметров и 16 квадратных сантиметров . Найдите площадь трапеции.
Площади треугольников АОD и ВОС равны соответственно 25 квадратных сантиметров и 16 квадратных сантиметров . Найдите площадь трапеции.
Слайд 52№ 26 (1) Найдите площадь круга, вписанного в
равнобедренную трапецию с большим основанием, равным 18, и острым углом 60°.
Слайд 53№26 (2) Найдите площадь прямоугольника, диагональ которого
равна 8, а угол между диагоналями 30°.
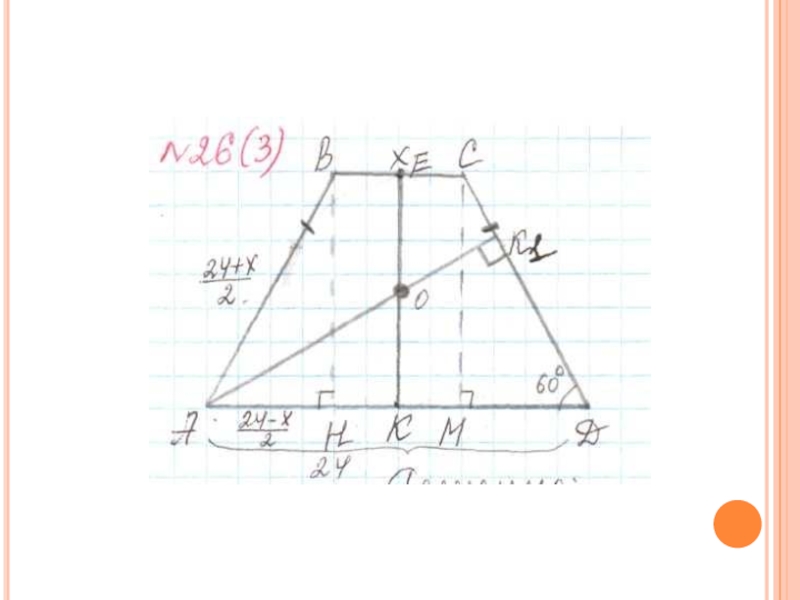
Слайд 54 №26 (3) Дана равнобедренная трапеция с углом
60° и большим основанием, равным 24. Прямая, проходящая через вершину острого угла и центр вписанной окружности, делит трапецию на четырехугольник и треугольник.
Найдите площадь полученного треугольника.
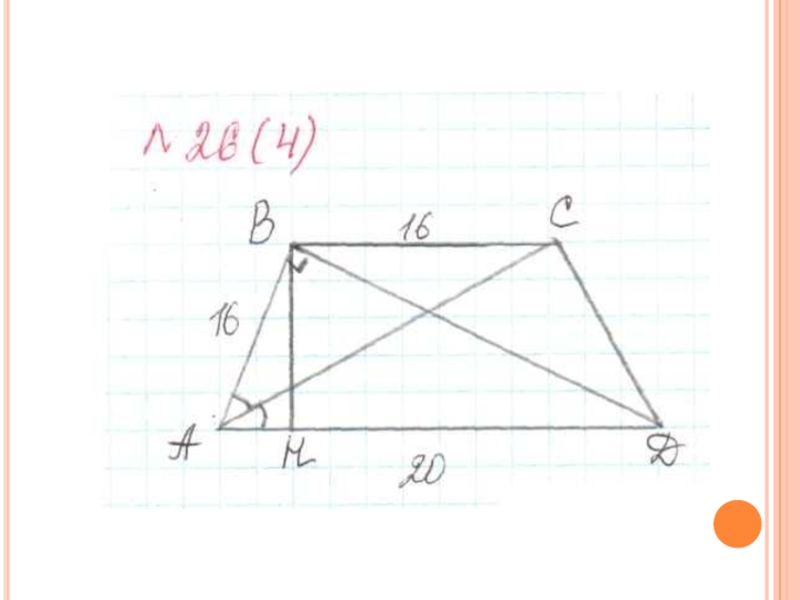
Слайд 56№26 (4)
Найдите площадь трапеции, если длина большего основания равна 20, длина одной из диагоналей перпендикулярна известной боковой стороне, а биссектрисой угла, образованного этой боковой стороной и большим основанием, служит вторая диагональ.
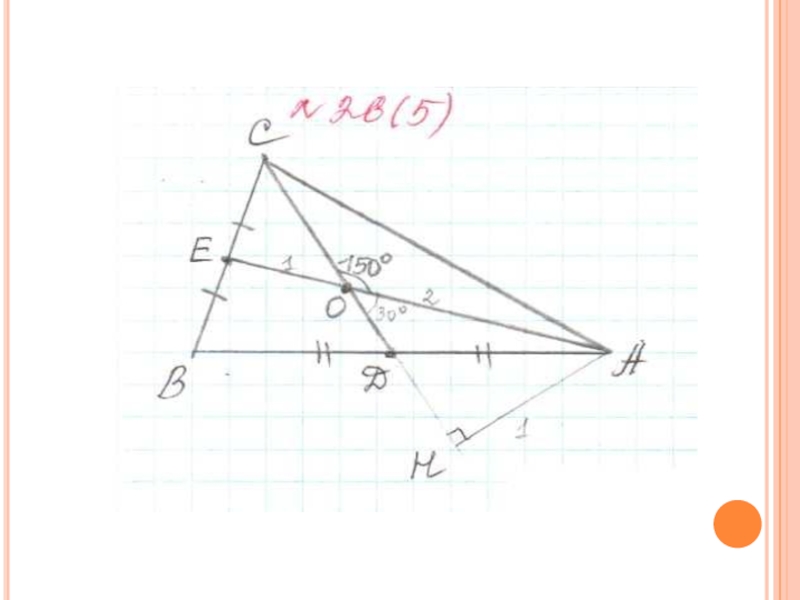
Слайд 58№26 (5) Площадь треугольника АВС равна 12 см². Медианы
АЕ и СD пересекаются в точке О. Угол АОС равен 150°, АЕ = 3 см найдите СD.