- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Технологии развитие смыслового чтения на уроках математики
Содержание
- 1. Технологии развитие смыслового чтения на уроках математики
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
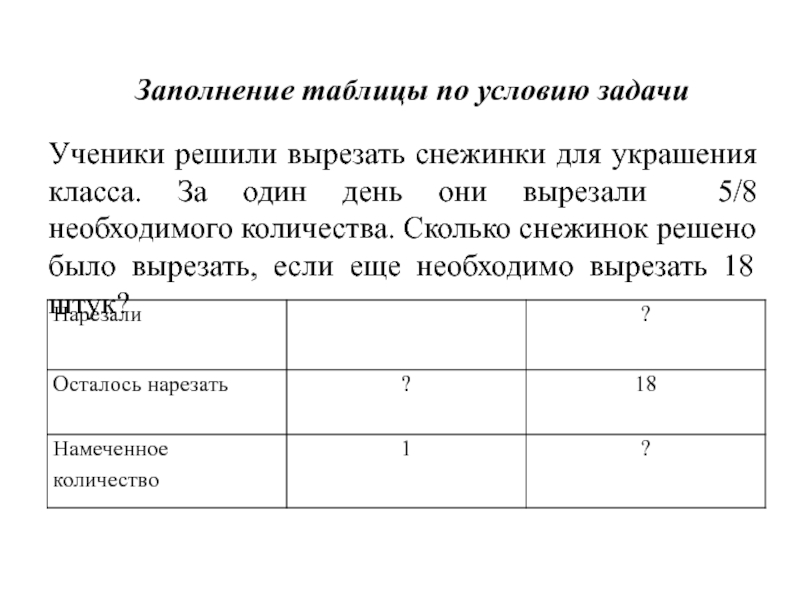
- 6. Заполнение таблицы по условию задачиУченики решили вырезать
- 7. Слайд 7
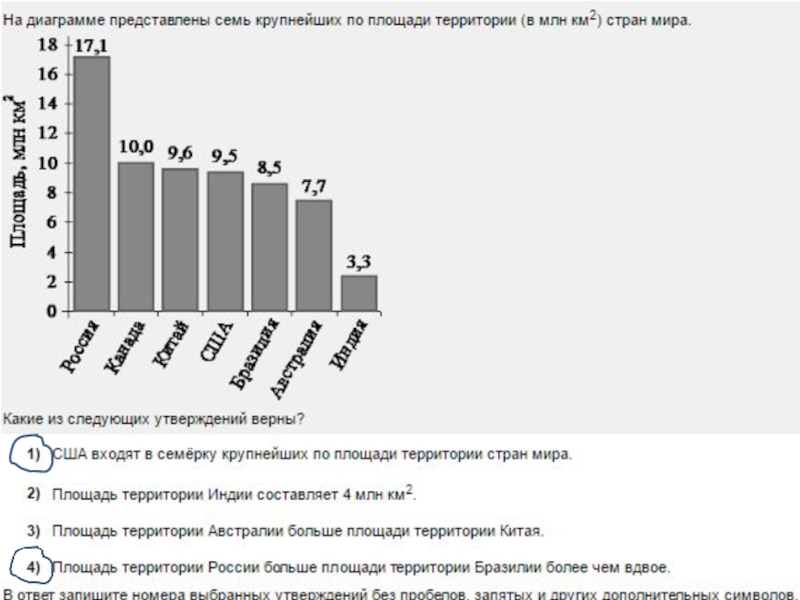
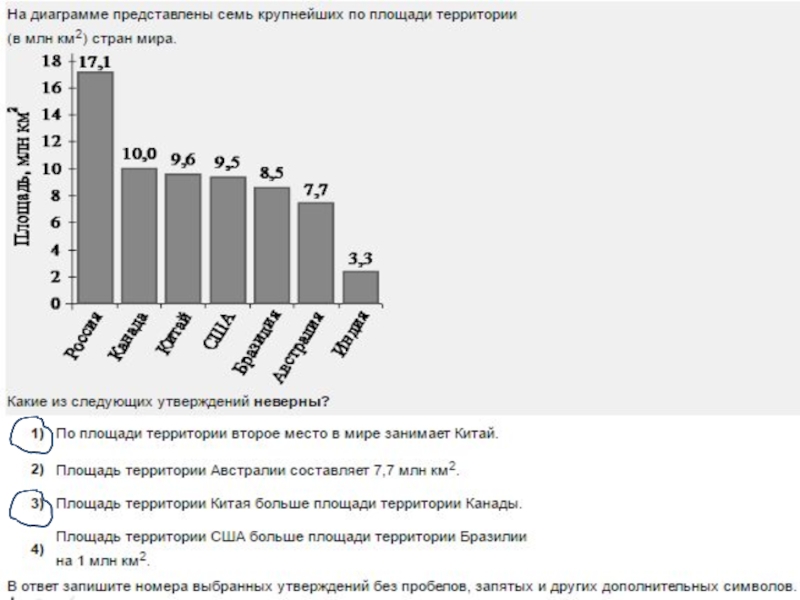
- 8. Чтобы справиться с решением задачи, учащиеся должны:-
- 9. Ключевые направления формирования умений работы с текстом.
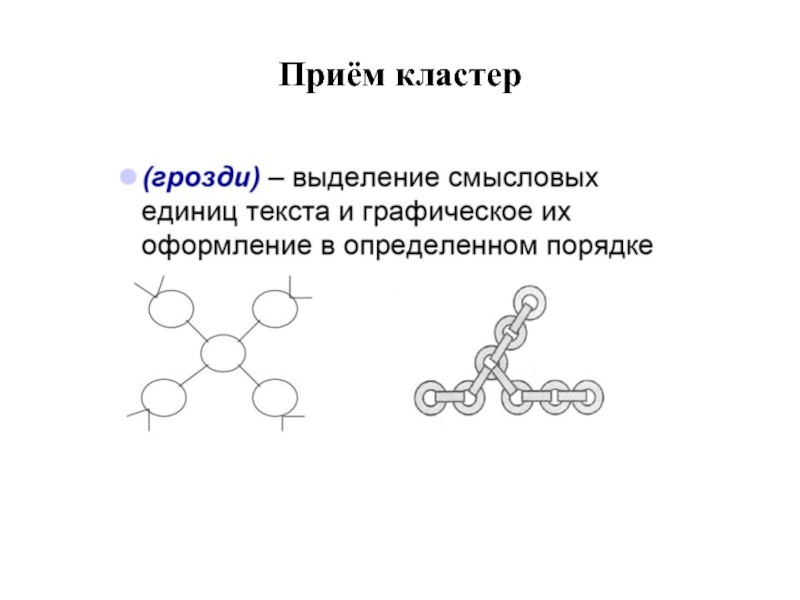
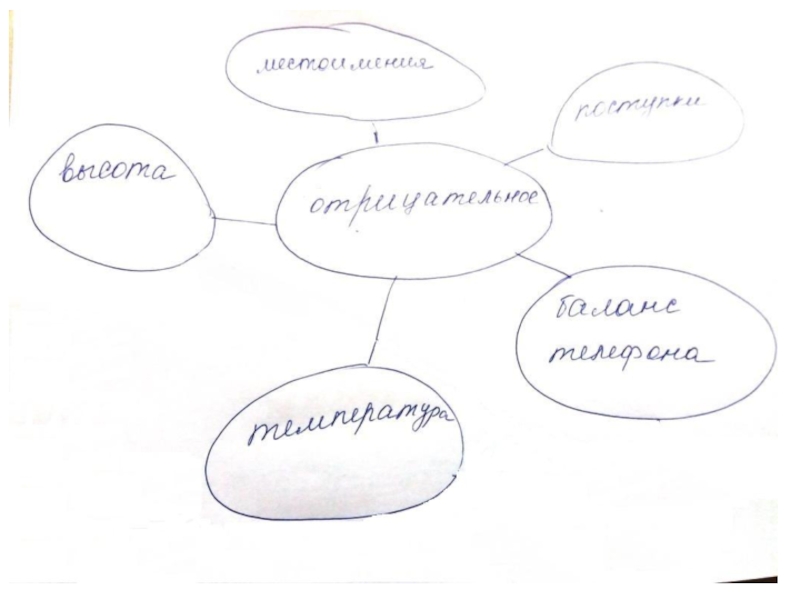
- 10. Приём кластер
- 11. В какой последовательности действовать, составляя кластер? Последовательность
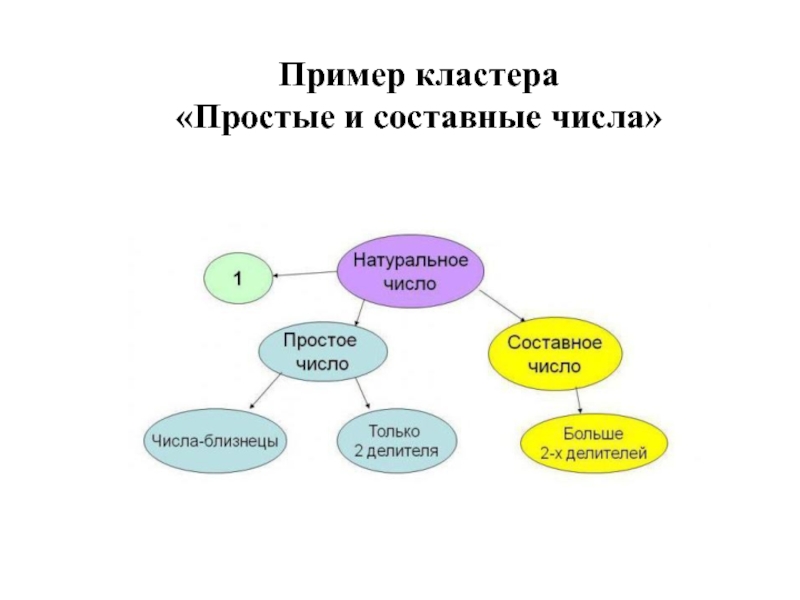
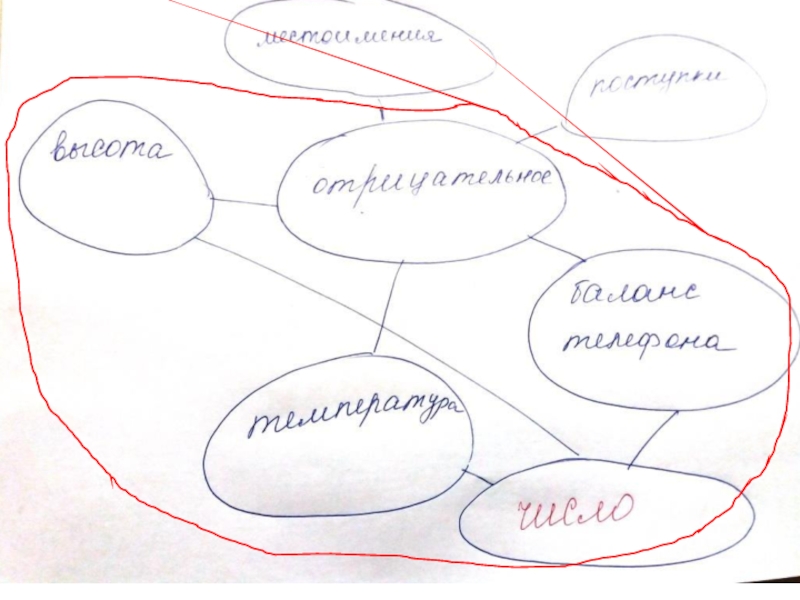
- 12. Пример кластера «Простые и составные числа»
- 13. ПропорцияРавенство отношенийЧлены пропорцииВерная пропорцияОсновное свойство пропорцииПроверка верности
- 14. Слово «пропорция» происходит от латинского слова proportio,
- 15. В Вавилоне с помощью пропорций рисовали планы
- 16. Слово «пропорция» ввел в употребление в I
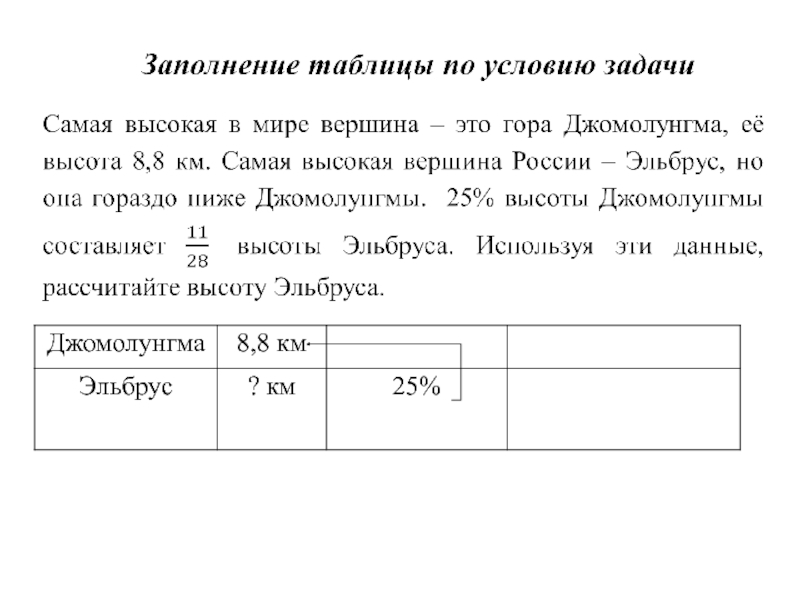
- 17. Слайд 17
- 18. Климатические условия Волгоградской областиКлимат области засушливый, с резко выраженной континентальностью. Северо-западная часть находится в зоне лесостепи, восточная — в зоне полупустынь, приближаясь к настоящим пустыням. Средне годовое количество осадков выпадает на северо-западе до 500 мм, на юго-востоке — менее 300 мм. Абсолютный максимум тепла +42…+44 °C наблюдается обычно в июле августе. Абсолютный минимум температуры воздуха составляет −36… −42 °C и наблюдается в январе — феврале.
- 19. Слайд 19
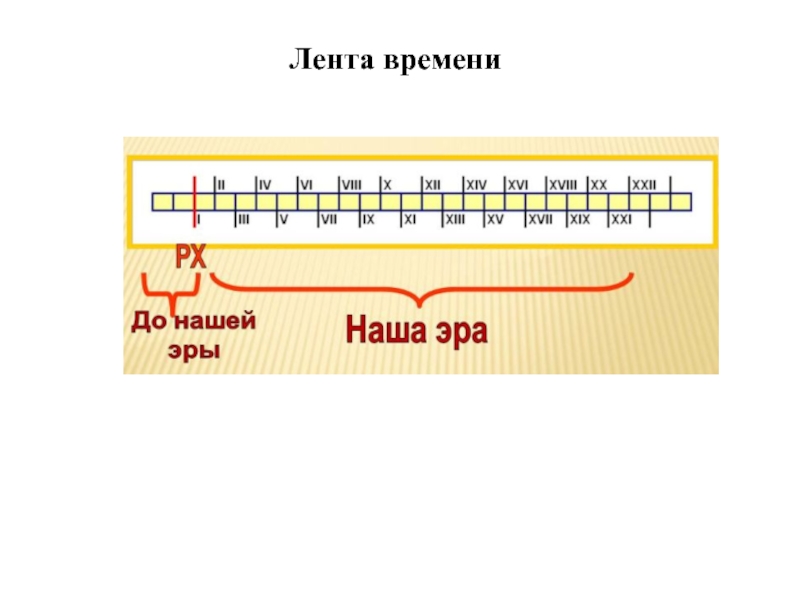
- 20. Лента времени
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Приём «кластер»: каковы достоинства и результаты применения
Заполнение таблицы по условию задачиУченики решили вырезать снежинки для украшения класса. За один день они вырезали 5/8 необходимого количества. Сколько снежинок решено было вырезать, если еще необходимо вырезать 18 штук?
Слайд 6Заполнение таблицы по условию задачи
Ученики решили вырезать снежинки для украшения класса.
За один день они вырезали 5/8 необходимого количества. Сколько снежинок решено было вырезать, если еще необходимо вырезать 18 штук?
Слайд 8Чтобы справиться с решением задачи, учащиеся должны:
- осмысленно читать и воспринимать
на слух текст задания;
- уметь извлекать и анализировать информацию, полученную из текста;
- уметь критически оценивать данную информацию;
- уметь читать таблицы, диаграммы, схемы, условные обозначения.
- уметь извлекать и анализировать информацию, полученную из текста;
- уметь критически оценивать данную информацию;
- уметь читать таблицы, диаграммы, схемы, условные обозначения.
Слайд 9Ключевые направления формирования умений работы с текстом.
• Найти доступ к
информации и извлечь ее
• Сформировать общее понимание текста и перевести информацию текста на язык читателя (интегрировать и интерпретировать, связывать и толковать)
• Размышлять о содержании и форме текстового сообщения, оценивать его.
• Сформировать общее понимание текста и перевести информацию текста на язык читателя (интегрировать и интерпретировать, связывать и толковать)
• Размышлять о содержании и форме текстового сообщения, оценивать его.
Слайд 11В какой последовательности действовать, составляя кластер?
Последовательность действий при составлении «грозди»
логична и проста. Посередине классной доски или чистого листа пишется ключевое слово или предложение, являющееся главным в раскрытии темы, идеи. Далее вокруг записываются другие слова или предложения, которые выражают факты, идеи, образы, подходящие для выбранной тематики. По мере записи все новые элементы соединяются прямой линией с ключевым понятием. Каждый «спутник», в свою очередь, тоже имеет «спутников» - так устанавливаются новые логические связи между понятиями.
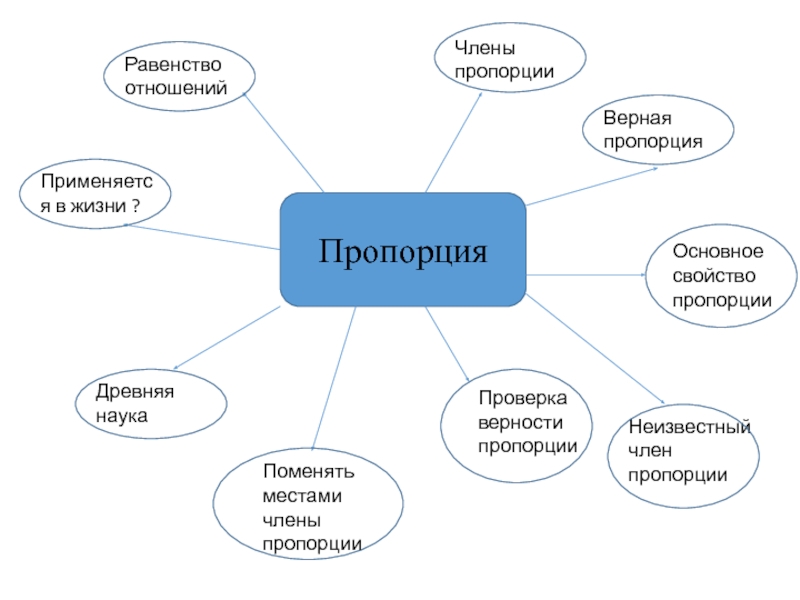
Слайд 13Пропорция
Равенство отношений
Члены пропорции
Верная пропорция
Основное свойство пропорции
Проверка верности пропорции
Древняя наука
Поменять местами члены
пропорции
Неизвестный член пропорции
Применяется в жизни ?
Слайд 14Слово «пропорция» происходит от латинского слова proportio, означающего соразмерность, определенное соотношение
частей между собой. Пропорции используют с древности при решении разных задач в математике.
Ещё в древней Греции математики использовали такой аппарат, как ПРОПОРЦИЯ. Пропорцией называют равенство отношений двух или нескольких пар чисел или величин. Первыми арифметическую теорию пропорций разработали древнегреческий ученый Пифагор (около 580-500 гг до н.э.) и его ученики.
В 4 веке до н.э. древнегреческий ученый Евдокс (около 408 – 355 гг. до н.э.) дал систематическое учение о пропорциях применительно не только к целым, но и к дробным числам.
Ещё в древней Греции математики использовали такой аппарат, как ПРОПОРЦИЯ. Пропорцией называют равенство отношений двух или нескольких пар чисел или величин. Первыми арифметическую теорию пропорций разработали древнегреческий ученый Пифагор (около 580-500 гг до н.э.) и его ученики.
В 4 веке до н.э. древнегреческий ученый Евдокс (около 408 – 355 гг. до н.э.) дал систематическое учение о пропорциях применительно не только к целым, но и к дробным числам.
Слайд 15В Вавилоне с помощью пропорций рисовали планы древних городов. На рисунке
изображен найденный при раскопках план древнего вавилонского города Ниппура. Когда ученые сравнили результаты раскопок города с этим планом, оказалось, что он сделан с большой точностью. В Вавилоне с помощью пропорций рисовали планы древних городов. На рисунке изображен найденный при раскопках план древнего вавилонского города Ниппура. Когда ученые сравнили результаты раскопок города с этим планом, оказалось, что он сделан с большой точностью
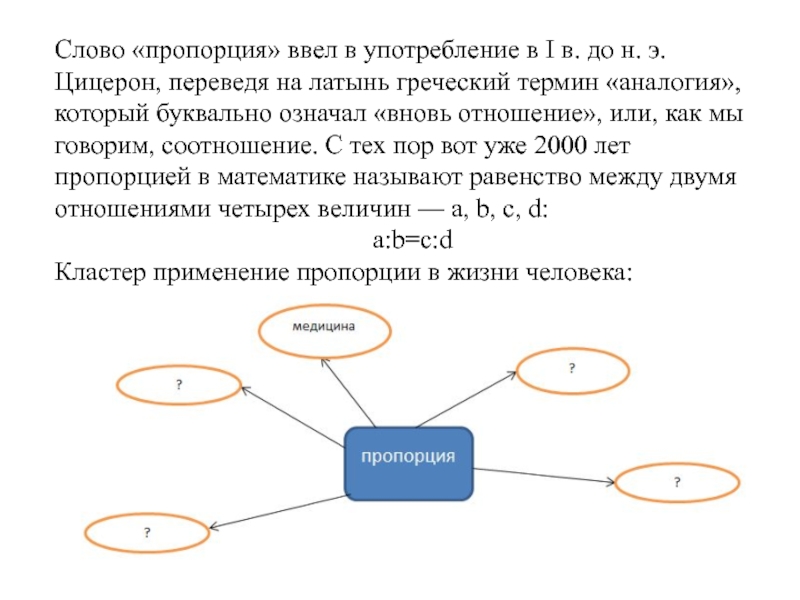
Слайд 16Слово «пропорция» ввел в употребление в I в. до н. э.
Цицерон, переведя на латынь греческий термин «аналогия», который буквально означал «вновь отношение», или, как мы говорим, соотношение. С тех пор вот уже 2000 лет пропорцией в математике называют равенство между двумя отношениями четырех величин — a, b, c, d:
a:b=c:d
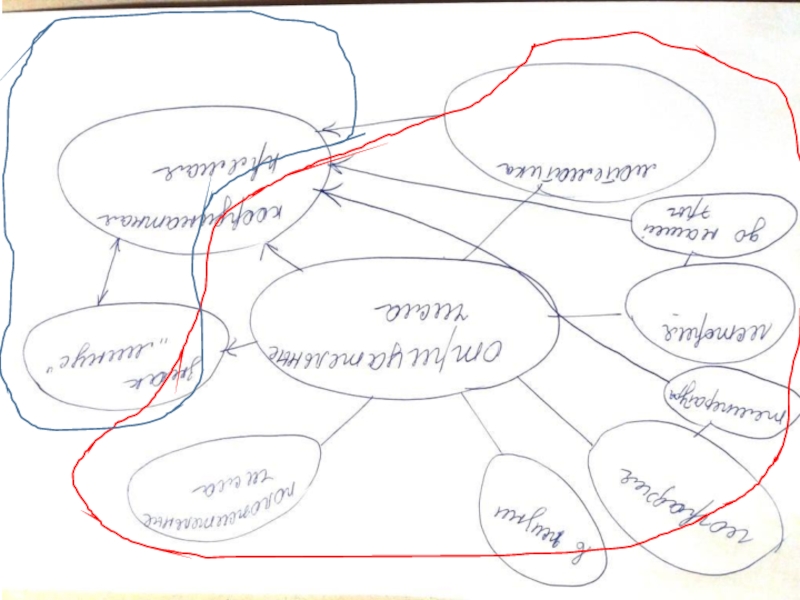
Кластер применение пропорции в жизни человека:
a:b=c:d
Кластер применение пропорции в жизни человека:
Слайд 18Климатические условия Волгоградской области
Климат области засушливый, с резко выраженной
континентальностью.
Северо-западная часть находится в зоне лесостепи, восточная — в зоне полупустынь, приближаясь к настоящим пустыням. Средне годовое количество осадков выпадает на северо-западе до 500 мм, на юго-востоке — менее 300 мм. Абсолютный максимум тепла +42…+44 °C наблюдается
обычно в июле августе. Абсолютный минимум температуры воздуха
составляет −36… −42 °C и наблюдается в январе — феврале.
Слайд 24Приём «кластер»: каковы достоинства и результаты применения этого метода?
Какие умения
формируются и развиваются в процессе данной работы?
Умение формулировать вопросы.
Находить главное в большом объеме учебного материала.
Устанавливать причинно-следственные и логические связи.
Строить умозаключения.
Переходить от частного к общему, воспринимая проблему в общем виде.
Проводить аналогии.
Умение формулировать вопросы.
Находить главное в большом объеме учебного материала.
Устанавливать причинно-следственные и логические связи.
Строить умозаключения.
Переходить от частного к общему, воспринимая проблему в общем виде.
Проводить аналогии.