- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тайны и загадки пирамид
Содержание
- 1. Тайны и загадки пирамид
- 2. Многогранник – это тело, граница которого состоит из кусков плоскостей ( многоугольников ). Эти многоугольники называются гранями,
- 3. ПризмаПризма – это многогранник ( рис.79 ), две грани которой ABCDE и abcde ( основания призмы ) – равные многоугольники с
- 4. ПараллелепипедПараллелепипед - это призма, основания которой параллелограммы.
- 5. ПирамидаПирамида – это многогранник, у которого одна
- 6. ПризматоидПризматоид - многогранник, ограниченный двумя многоугольниками, расположенными
- 7. Тела ПлатонаМногогранник, все грани которого представляют собой
- 8. ТетраэдрТетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).
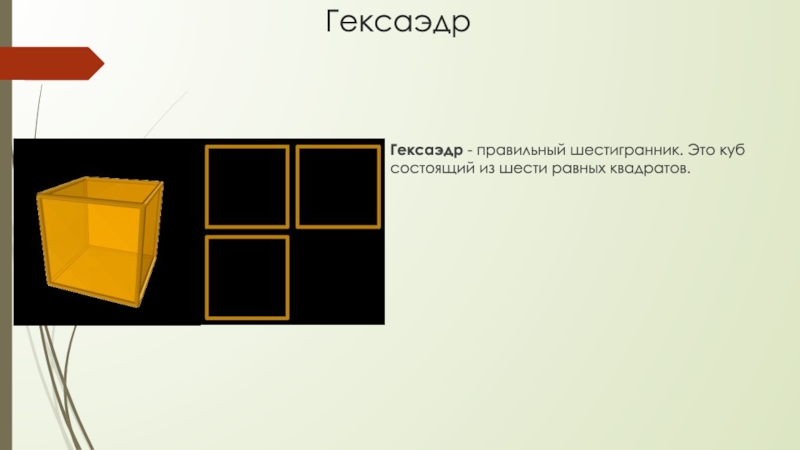
- 9. ГексаэдрГексаэдр - правильный шестигранник. Это куб состоящий из шести равных квадратов.
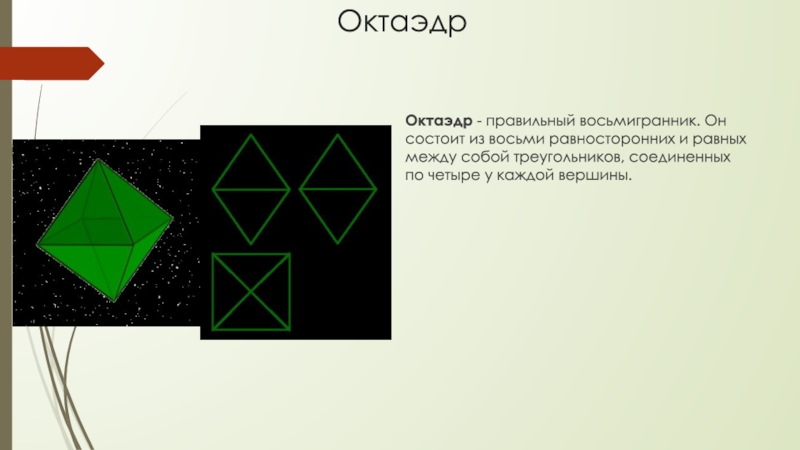
- 10. ОктаэдрОктаэдр - правильный восьмигранник. Он состоит из
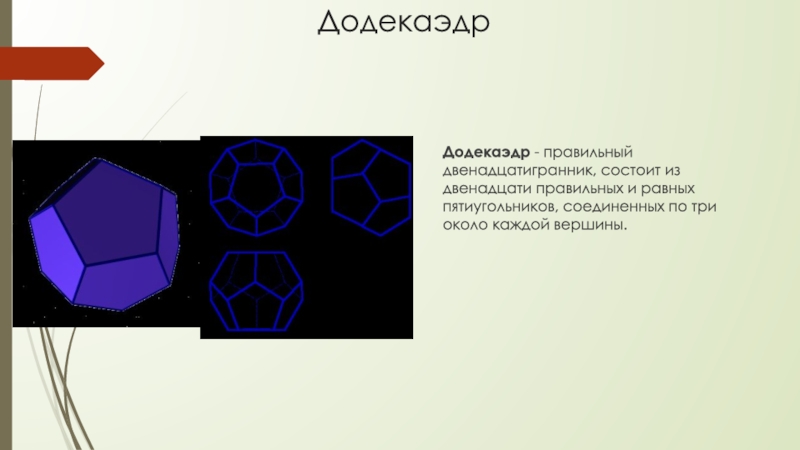
- 11. ДодекаэдрДодекаэдр - правильный двенадцатигранник, состоит из двенадцати
- 12. ИкосаэдрИкосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины.
- 13. Звездчатые формы и соединения тел Платона.Кроме правильных
- 14. Малый звездчатый додекаэдр - звездчатый додекаэдр первого
- 15. Использованная литератураЛитература 1. Адамар Ж. Элементарная геометрия.
- 16. Сделал: Зубенко С.С. Под руководством: Поздняковой А.В.
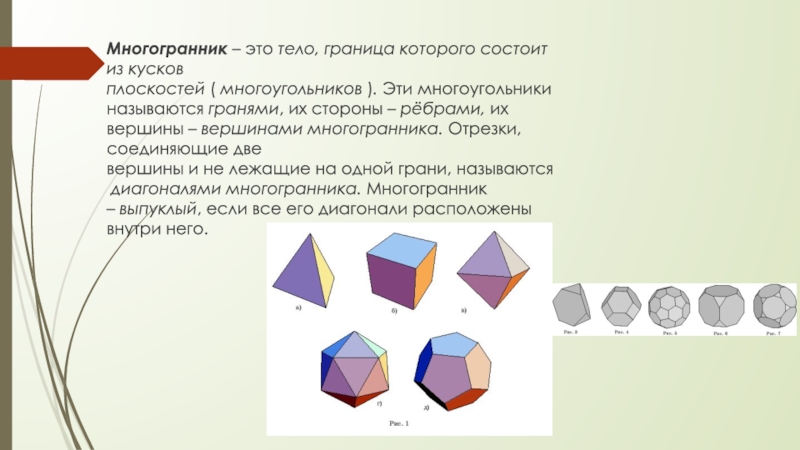
Многогранник – это тело, граница которого состоит из кусков плоскостей ( многоугольников ). Эти многоугольники называются гранями, их стороны – рёбрами, их вершины – вершинами многогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналями многогранника. Многогранник – выпуклый, если все его диагонали расположены внутри него.
Слайд 2Многогранник – это тело, граница которого состоит из кусков плоскостей ( многоугольников ). Эти многоугольники называются гранями, их стороны – рёбрами, их вершины –
вершинами многогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналями многогранника. Многогранник – выпуклый, если все его диагонали расположены внутри него.
Слайд 3Призма
Призма – это многогранник ( рис.79 ), две грани которой ABCDE и abcde ( основания призмы ) – равные многоугольники с соответственно параллельными сторонами, а
остальные грани ( AabB, BbcC и т.д. ) - параллелограммы, плоскости которых параллельны прямой ( Aa, или Bb, или Cc и т.д. ). Параллелограммы AabB, BbcC и т.д. называются боковыми гранями; рёбра Aa, Bb, Cc и т.д. называются боковыми рёбрами. Высота призмы – это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания. В зависимости от формы многоугольника, лежащего в основании, призма может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Если боковые рёбра призмы перпендикулярны к плоскости основания, то такая призма называется прямой; в противном случае – это наклонная призма. Если в основании прямой призмы лежит правильный многоугольник, то такая призма также называется правильной. На рис.79 показана наклонная призма.
Слайд 4Параллелепипед
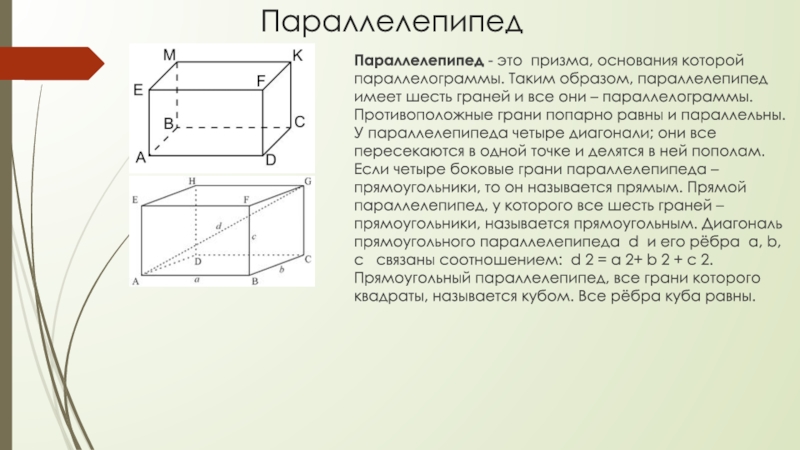
Параллелепипед - это призма, основания которой параллелограммы. Таким образом, параллелепипед имеет
шесть граней и все они – параллелограммы. Противоположные грани попарно равны и параллельны. У параллелепипеда четыре диагонали; они все пересекаются в одной точке и делятся в ней пополам. Если четыре боковые грани параллелепипеда – прямоугольники, то он называется прямым. Прямой параллелепипед, у которого все шесть граней – прямоугольники, называется прямоугольным. Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением: d 2 = a 2+ b 2 + c 2. Прямоугольный параллелепипед, все грани которого квадраты, называется кубом. Все рёбра куба равны.
Слайд 5Пирамида
Пирамида – это многогранник, у которого одна грань ( основание пирамиды
) – это произвольный многоугольник ( ABCDE, рис.80 ), а остальные грани ( боковые грани ) – треугольники с общей вершиной S, называемой вершиной пирамиды. Перпендикуляр SO, опущенный из вершины пирамиды на её основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Треугольная пирамида является тетраэдром ( четырёхгранником ), четырёхугольная – пятигранником и т.д. Пирамида называется правильной, если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани (SF) называется апофемой правильной пирамиды.
Если провести сечение abcde, параллельное основанию ABCDE ( рис.81 ) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями; расстояние Oo между ними – высотой. Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная. Все боковые грани правильной усечённой пирамиды – равные равнобочные трапеции. Высота Ff боковой грани ( рис.81 ) называется апофемой правильной усечённой пирамиды.
Если провести сечение abcde, параллельное основанию ABCDE ( рис.81 ) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями; расстояние Oo между ними – высотой. Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная. Все боковые грани правильной усечённой пирамиды – равные равнобочные трапеции. Высота Ff боковой грани ( рис.81 ) называется апофемой правильной усечённой пирамиды.
Слайд 6Призматоид
Призматоид - многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они
являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований.
Слайд 7Тела Платона
Многогранник, все грани которого представляют собой правильные и равные многоугольники,
называют правильными. Углы при вершинах такого многогранника равны между собой.
Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.
Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.
Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
Слайд 8Тетраэдр
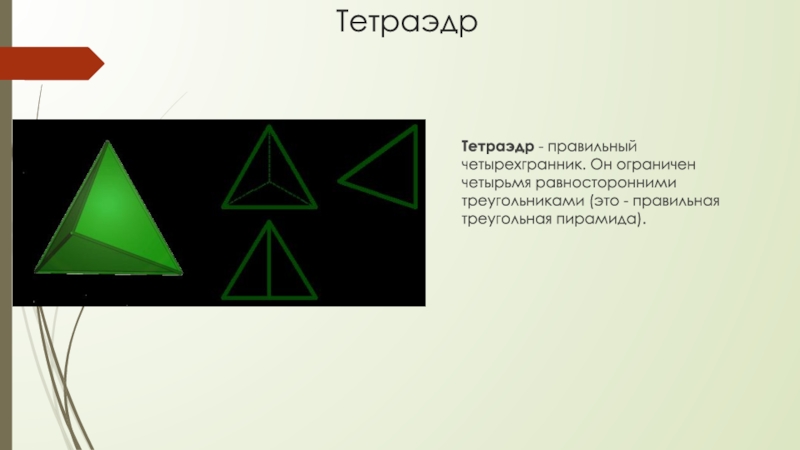
Тетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это -
правильная треугольная пирамида).
Слайд 10Октаэдр
Октаэдр - правильный восьмигранник. Он состоит из восьми равносторонних и равных
между собой треугольников, соединенных по четыре у каждой вершины.
Слайд 11Додекаэдр
Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников,
соединенных по три около каждой вершины.
Слайд 12Икосаэдр
Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по
пять около каждой вершины.
Слайд 13Звездчатые формы и соединения тел Платона.
Кроме правильных выпуклых многогранников существуют и
правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.
Звездчатый октаэдр - восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру. Это малые тетраэдры, основания которых совпадают с гранями октаэдра. Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula - восьмиугольная звезда.
Звездчатый октаэдр - восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру. Это малые тетраэдры, основания которых совпадают с гранями октаэдра. Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula - восьмиугольная звезда.
Слайд 14Малый звездчатый додекаэдр - звездчатый додекаэдр первого продолжения. Он образован продолжением
граней выпуклого додекаэдра до их первого пересечения. Каждая грань выпуклого додекаэдра при продолжении образует правильный звездчатый пятиугольник. Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые "куски", внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра. При дальнейшем продолжении граней до нового пересечения образуется средний звездчатый додекаэдр - звездчатый додекаэдр второго продолжения. Последней же звездчатой формой правильного додекаэдра является звездчатый додекаэдр третьего продолжения - большой звездчатый додекаэдр. Он образован продолжением граней звездчатого додекаэдра второго продолжения до их нового пересечения.
Слайд 15Использованная литература
Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. –
М.: Учпедгиз, 1938 (или более поздние издания, например, 3-е изд., 1958). Книга VI. Многогранники. Дополнения: Глава V.
2. Александров А.Д. Выпуклые многогранники. – М.-Л.; 1950.
3. Болл У., Коксетер Г. Математические эссе и развлечения. – М.: Мир, 1986, с.142.
4. Долбилин Н.П. Жемчужины теории многогранников. – М.: МЦНМО, 2000, с.27-31.
5. Люстерник Л.А. Выпуклые фигуры и многогранники. – М.; 1956.
6. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949, с. 34, с.268.
7. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
8. Энциклопедия элементарной математики. Книга IV. Геометрия. - М.; 1963, с. 382.
9. Яглом И.М., Болтянский В.Г. Выпуклые фигуры. – М.-Л.; 1951 /Библиотека математического кружка, выпуск 4.
2. Александров А.Д. Выпуклые многогранники. – М.-Л.; 1950.
3. Болл У., Коксетер Г. Математические эссе и развлечения. – М.: Мир, 1986, с.142.
4. Долбилин Н.П. Жемчужины теории многогранников. – М.: МЦНМО, 2000, с.27-31.
5. Люстерник Л.А. Выпуклые фигуры и многогранники. – М.; 1956.
6. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949, с. 34, с.268.
7. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
8. Энциклопедия элементарной математики. Книга IV. Геометрия. - М.; 1963, с. 382.
9. Яглом И.М., Болтянский В.Г. Выпуклые фигуры. – М.-Л.; 1951 /Библиотека математического кружка, выпуск 4.