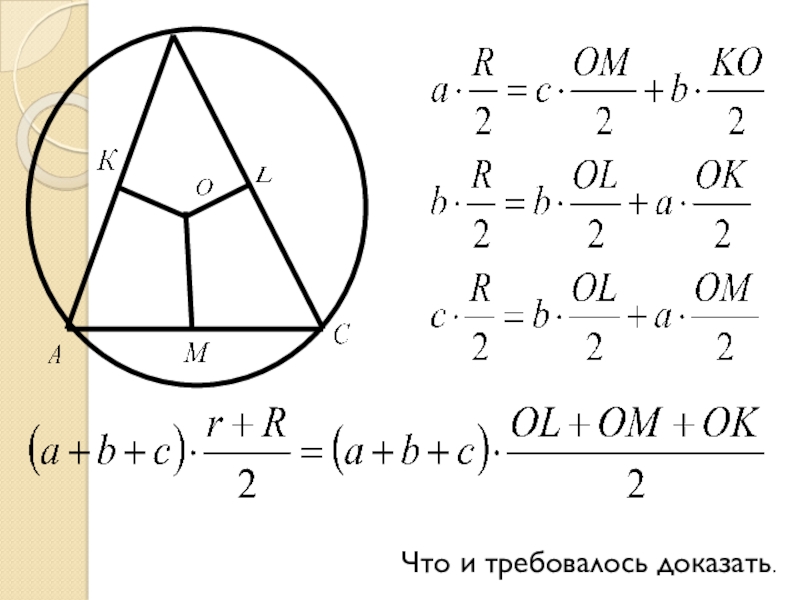- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Старая японская теорема. НПК учеников
Содержание
- 1. Старая японская теорема. НПК учеников
- 2. Теорема (1800 год)Разобьем выпуклый многоугольник, вписанный в
- 3. Та же самая сумма радиусов получается и для любого другого разбиения данного многоугольника на треугольники
- 4. Теорема КарноСумма расстояний от центра окружности, описанной
- 5. Перенумеруем эти треугольники, и пусть ri —
- 6. Теорема Птолемея Произведение длин диагоналей вписанного четырехугольника равняется сумме произведений длин противоположных сторон этого четырехугольникаAC·BD=AB·CD+AD·BCСDAB
- 7. Доказательство теоремы ПтолемеяB
- 8. Доказательство теоремы КарноК четырехугольнику АКОМ можно
- 9. Что и требовалось доказать.
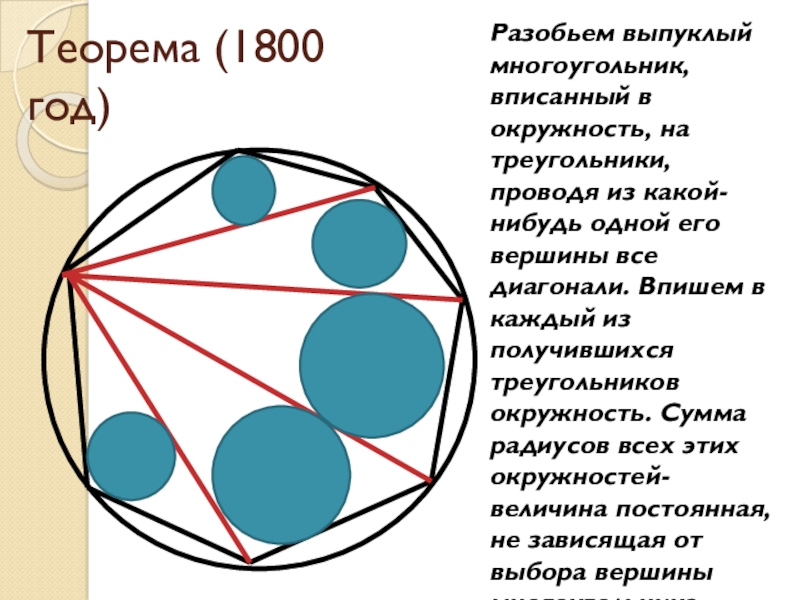
Теорема (1800 год)Разобьем выпуклый многоугольник, вписанный в окружность, на треугольники, проводя из какой-нибудь одной его вершины все диагонали. Впишем в каждый из получившихся треугольников окружность. Сумма радиусов всех этих окружностей- величина постоянная, не зависящая от выбора
Слайд 2Теорема (1800 год)
Разобьем выпуклый многоугольник, вписанный в окружность, на треугольники, проводя
из какой-нибудь одной его вершины все диагонали. Впишем в каждый из получившихся треугольников окружность. Сумма радиусов всех этих окружностей- величина постоянная, не зависящая от выбора вершины многоугольника
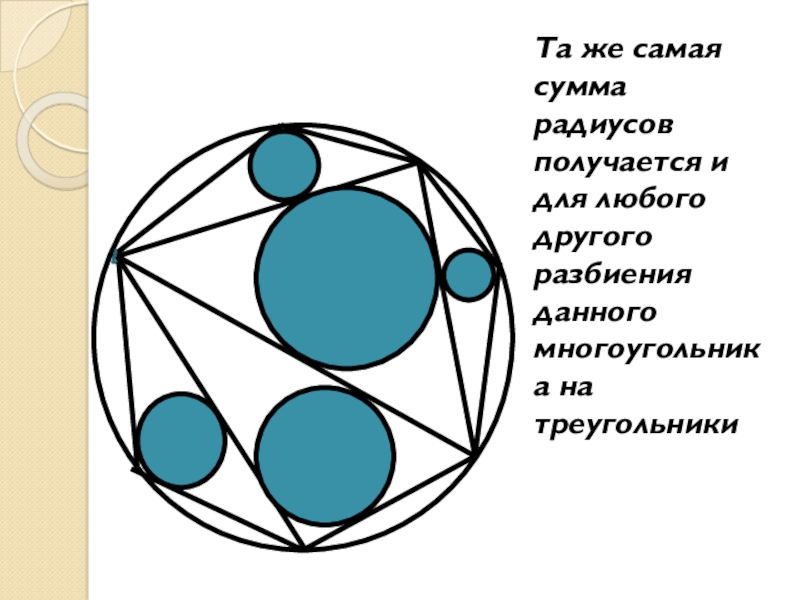
Слайд 3Та же самая сумма радиусов получается и для любого другого разбиения
данного многоугольника на треугольники
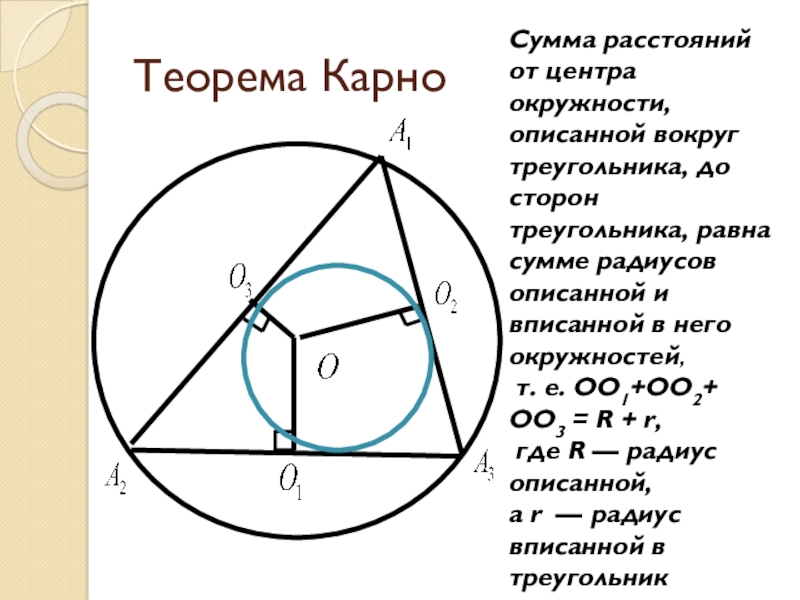
Слайд 4Теорема Карно
Сумма расстояний от центра окружности, описанной вокруг треугольника, до сторон
треугольника, равна сумме радиусов описанной и вписанной в него окружностей,
т. е. OO1+OO2+ ОО3 = R + r,
где R — радиус описанной,
а r — радиус вписанной в треугольник окружности.
т. е. OO1+OO2+ ОО3 = R + r,
где R — радиус описанной,
а r — радиус вписанной в треугольник окружности.
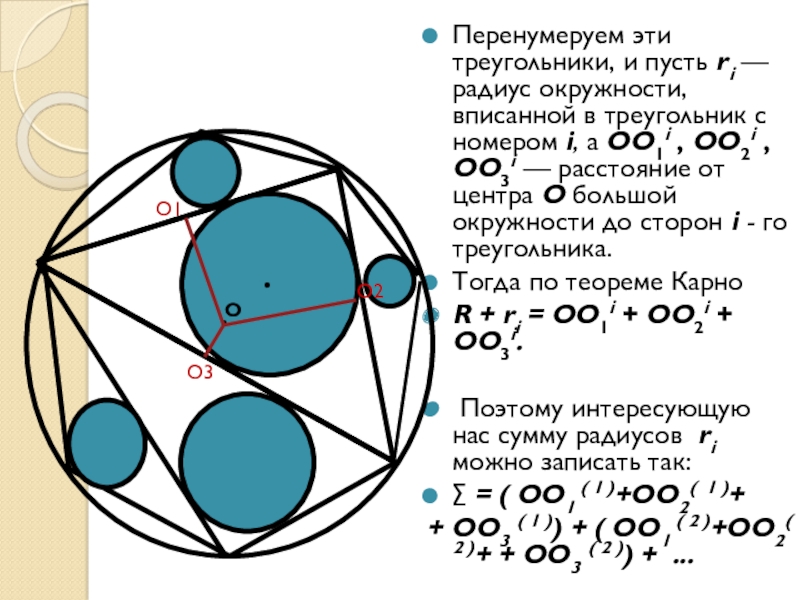
Слайд 5Перенумеруем эти треугольники, и пусть ri — радиус окружности, вписанной в
треугольник с номером i, а ОО1i , ОО2i , ОО3i — расстояние от центра О большой окружности до сторон i - гo треугольника.
Тогда по теореме Карно
R + ri = ОО1i + ОО2i + ОО3i.
Поэтому интересующую нас сумму радиусов ri можно записать так:
∑ = ( OO1 ( 1 )+OO2( 1 )+
+ ОО3 ( 1 )) + ( OO1 ( 2 )+OO2( 2 )+ + ОО3 ( 2 )) + ...
Тогда по теореме Карно
R + ri = ОО1i + ОО2i + ОО3i.
Поэтому интересующую нас сумму радиусов ri можно записать так:
∑ = ( OO1 ( 1 )+OO2( 1 )+
+ ОО3 ( 1 )) + ( OO1 ( 2 )+OO2( 2 )+ + ОО3 ( 2 )) + ...
•
О
•
О1
О2
О3
Слайд 6Теорема Птолемея
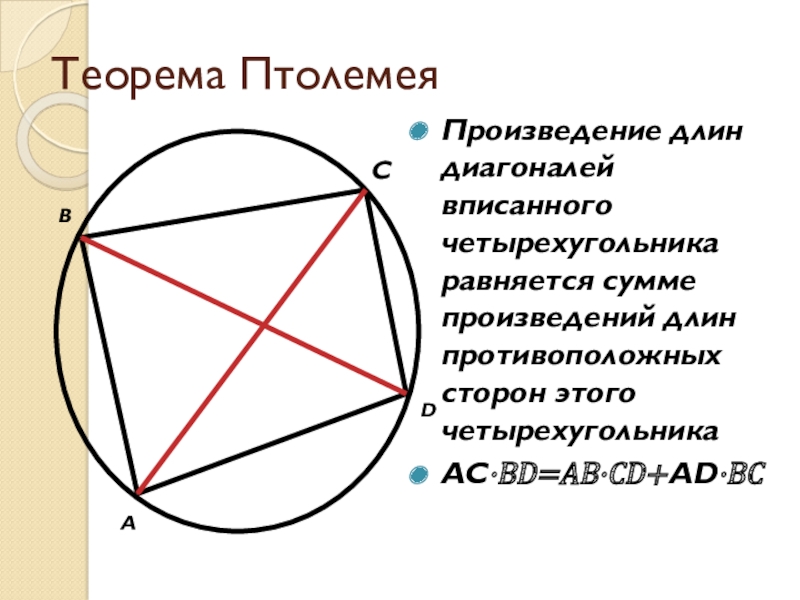
Произведение длин диагоналей вписанного четырехугольника равняется сумме произведений длин
противоположных сторон этого четырехугольника
AC·BD=AB·CD+AD·BC
AC·BD=AB·CD+AD·BC
С
D
A
B
Слайд 7Доказательство теоремы Птолемея
B
C
D
A
1
2
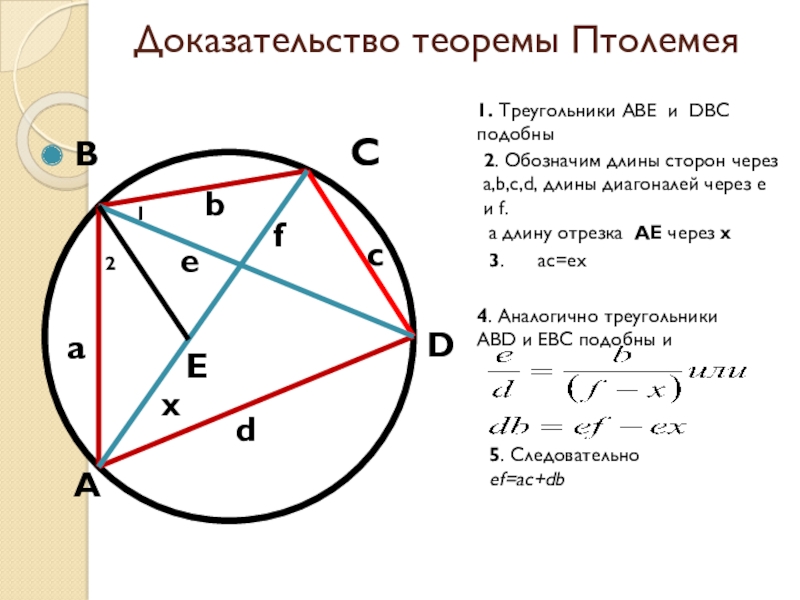
1. Треугольники ABE и DBC подобны
а
d
e
f
c
b
x
E
2. Обозначим длины сторон через a,b,c,d, длины диагоналей через e и f.
а длину отрезка АЕ через х
3. ас=ех
4. Аналогично треугольники ABD и EBC подобны и
5. Следовательно
ef=ac+db
Слайд 8Доказательство теоремы Карно
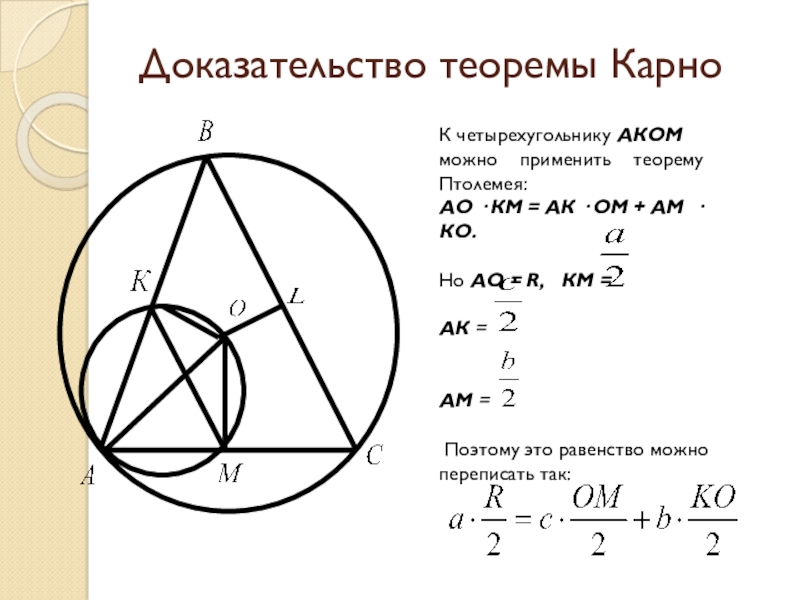
К четырехугольнику АКОМ можно применить теорему
Птолемея:
АО · КМ = АК · ОМ + АМ · КО.
Но AO = R, КМ =
АК =
АМ =
Поэтому это равенство можно переписать так:
АО · КМ = АК · ОМ + АМ · КО.
Но AO = R, КМ =
АК =
АМ =
Поэтому это равенство можно переписать так: