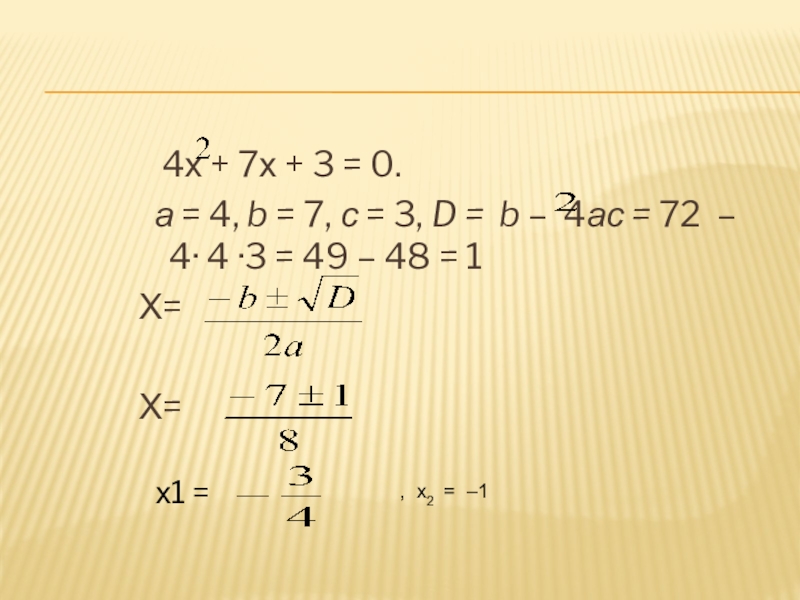уравнений.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Способы решения квадратных уравнений
Содержание
- 1. Способы решения квадратных уравнений
- 2. Определение квадратного уравнения, его виды Квадратным уравнением
- 3. Из истории квадратных уравнений Квадратные уравнения в
- 4. Квадратные уравнения в Индии Задачи на квадратные
- 5. Квадратные уравнения в Европе XIII-XVII вв. Формулы
- 6. Квадратные уравнения в Европе XIII-XVII вв. В
- 7. Различные способы решения квадратных уравнений 1. Разложение
- 8. Разложение левой части уравнения на множители
- 9. Метод выделения полного квадрата Решим уравнение х
- 10. Решение квадратных уравнений по формуле Х1,2 =
- 11. 4х + 7х +
- 12. 4х – 4х + 1 = 0,а
- 13. 2х +3х + 4 = 0
- 14. Решение уравнений с использованием теоремы Виета
- 15. Теорема Виета для квадратного уравнения Aх +вх +с = 0 имеет вид
- 16. ПримерыРешить уравнение х – 9х +
- 17. Примеры Решим уравнение 2х – 11х +
- 18. Свойства коэффициентов квадратного уравнения. Если а +
- 19. Решим уравнение 345х – 137х – 208
- 20. Если второй коэффициент b = 2k –
- 21. Графическое решение квадратного уравнения Решим графически уравнение
- 22. Слайд 22
- 23. квадратные уравнения играют огромную роль в развитии
Определение квадратного уравнения, его виды Квадратным уравнением называется уравнение вида a + bx + c = 0, где х- переменная, а,b и с-некоторые числа, причем, а ≠ 0.
Слайд 2Определение квадратного уравнения, его виды
Квадратным уравнением называется уравнение вида
a + bx + c = 0,
где х- переменная, а,b и с-некоторые числа, причем, а ≠ 0.
где х- переменная, а,b и с-некоторые числа, причем, а ≠ 0.
Слайд 3Из истории квадратных уравнений
Квадратные уравнения в Древнем Вавилоне
Квадратные уравнения умели
решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Слайд 4Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в
астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта(VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах2+вх=с, а0.
В этом уравнении коэффициенты, кроме а,могут быть и отрицатель-ными. Правило Брахмагупты по существу совпадает с нашим.
ах2+вх=с, а0.
В этом уравнении коэффициенты, кроме а,могут быть и отрицатель-ными. Правило Брахмагупты по существу совпадает с нашим.
Слайд 5Квадратные уравнения в Европе XIII-XVII вв.
Формулы решения квадратных уравнений по
образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи.Книга способствовала распространению алгебраических знаний в Италии, в Германии, Франции и др. странах Европы.
Слайд 6Квадратные уравнения в Европе XIII-XVII вв.
В глубокой древности была найдена
формула для решения квадратного уравнения с помощью радикалов (корней). Вывод формулы имеется у Виета,но он признавал только положительные корни. Итальянские математики Тарталья, Кордано, Бомбелли в XVI в.учитывают и отрицательные корни. В XVII в. благодаря трудам Жирара, Декарта, Ньютона способ решения квадратных уравнений принимает современный вид.
Слайд 7Различные способы решения квадратных уравнений
1. Разложение левой части уравнения на
множители
Решим уравнение х2 + 10х – 24 = 0.
Разложим левую часть уравнения на множители:
х2 + 10х – 24 = х2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х – 2) = 0.
Решим уравнение х2 + 10х – 24 = 0.
Разложим левую часть уравнения на множители:
х2 + 10х – 24 = х2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х – 2) = 0.
Слайд 8Разложение левой части уравнения на множители
Так как произведение равно нулю,
то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = - 12. это означает, что числа 2 и – 12 являются корнями уравнения х2 + 10х – 24 = 0.
Слайд 9Метод выделения полного квадрата
Решим уравнение х + 6х – 7
= 0
Выделим в левой части полный квадрат.
Выделим в левой части полный квадрат.
Слайд 11
4х + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b – 4ас = 72 – 4· 4 ·3 = 49 – 48 = 1
Х=
Х=
Х=
Х=
, х2 = –1
х1 =
Слайд 132х +3х + 4 = 0
а =2, b= 3,
с = 4
D = b – 4ас=9 – 4∙2∙4 =9 – 32 =
- 13
D < 0. Уравнение не имеет корней.
D = b – 4ас=9 – 4∙2∙4 =9 – 32 =
- 13
D < 0. Уравнение не имеет корней.
Слайд 14 Решение уравнений с использованием теоремы Виета
(прямой и обратной)
Как известно, приведенное
квадратное уравнение имеет вид
+ px + q = 0.
Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
+ px + q = 0.
Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
Слайд 16Примеры
Решить уравнение х – 9х + 14 =0
Попробуем найти два
числа х и х ,
такие, что х +х = 9 ,х х = 14
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
такие, что х +х = 9 ,х х = 14
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
Слайд 17Примеры
Решим уравнение 2х – 11х + 15 = 0.
«Перебросим» коэффициент
2 к свободному члену, в результате получим уравнение у – 11y +30 = 0.
Согласно теореме Виета
Согласно теореме Виета
Слайд 18Свойства коэффициентов квадратного уравнения.
Если а + b + с =
0 (т.е. сумма коэффициентов уравнения равна нулю),
то х1 = 1, х2 = .
Если а - b + с = 0, или b = а + с, то
х1 = – 1, х2 = –
то х1 = 1, х2 = .
Если а - b + с = 0, или b = а + с, то
х1 = – 1, х2 = –
Слайд 19Решим уравнение 345х – 137х – 208 = 0.
Так как а
+ b + с = 0 (345 – 137 – 208 = 0)
, то х1 = 1, х2 = .
Решим уравнение
132х + 247х + 115 = 0
Т. к. а-b+с = 0 (132 – 247 +115=0), то
х1= - 1, х2= -
, то х1 = 1, х2 = .
Решим уравнение
132х + 247х + 115 = 0
Т. к. а-b+с = 0 (132 – 247 +115=0), то
х1= - 1, х2= -
Слайд 21Графическое решение квадратного уравнения
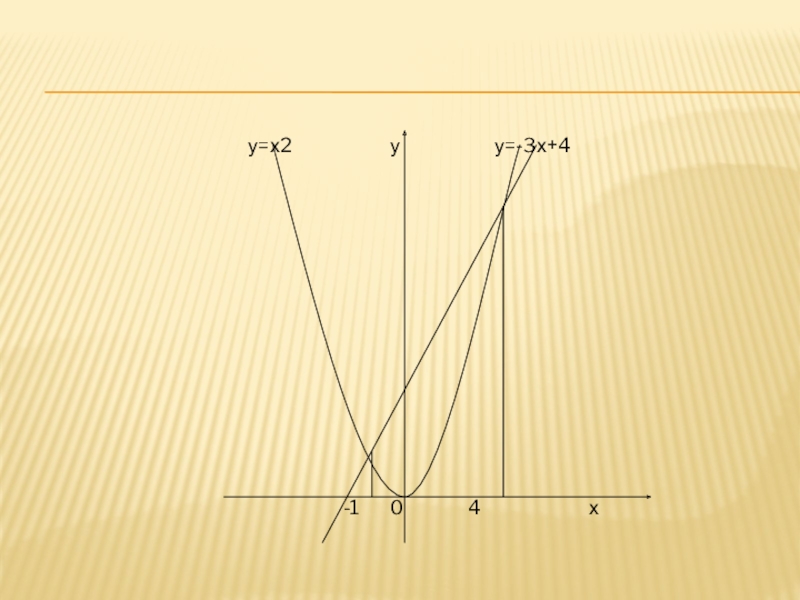
Решим графически уравнение
х – 3х
– 4 = 0.
Решение. Запишем уравнение в виде
х = 3х + 4 . Построим параболу у = х и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13).
Прямая и парабола пересекаются в двух точках А и B с абсциссами х1 = – 1 и
х2 = 4.
Решение. Запишем уравнение в виде
х = 3х + 4 . Построим параболу у = х и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13).
Прямая и парабола пересекаются в двух точках А и B с абсциссами х1 = – 1 и
х2 = 4.
Слайд 23квадратные уравнения играют огромную роль в развитии математики. Все мы умеем
решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.
Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников.