ЛОГАРИФМЫ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Седьмое математическое действие
Содержание
- 1. Седьмое математическое действие
- 2. СЕДЬМОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ Раскрыть содержание таких важных
- 3. «Изобретение
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. ФОРМУЛА ПЕРЕХОДА ОТ ОДНОГО ОСНОВАНИЯ К ДРУГОМУ
- 9. 1. Область определения: D (y) = (0;
- 10. Слайд 10
- 11. Номера клавишей рояля представляют собой логарифмы чисел
- 12. Оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов, составленной при основании 2,5.
- 13. Громкость шума, выраженная в белах, равна десятичному логарифму его физической силы.
- 14. Слайд 14
- 15. Решение.О.Д.З.По определению логарифма:Ответ: 4,5.Логарифмические уравнения
- 16. Логарифмические уравненияРешение.О.Д.З.По определению логарифма:Ответ: 22.
- 17. Решение.О.Д.З.Ответ: – 6.Логарифмические уравнения
- 18. О.Д.З.Домашнее задание
- 19. Решение.О.Д.З.По определению логарифма:Ответ: 0,6.Домашнее задание
- 20. О.Д.З.Ответ: 2.Домашнее задание
- 21. Решение.О.Д.З.Логарифмические неравенства
- 22. Решение.О.Д.З.Логарифмические неравенства
- 23. № 1. Вычислить:Консультация
- 24. Консультация
- 25. Консультация
- 26. Решение.О.Д.З.По определению логарифма:Ответ: 2.Консультация
- 27. Решение.О.Д.З.Консультация
- 28. «С точки зрения вычислительной практики, изобретение логарифмов
- 29. СЕДЬМОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ Информационные источникиМатематика: учебник для
СЕДЬМОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ Раскрыть содержание таких важных понятий как логарифм, логарифмическая функция, логарифмическое уравнение, логарифмическое неравенство.Обеспечить овладение практическими приемами преобразования выражений, содержащих логарифмы, построения графика логарифмической функции.Сформировать навыки решения логарифмических уравнений и неравенств, характерных для программных
Слайд 1Краевое государственное бюджетное образовательное
учреждение начального профессионального образования
«Профессиональное училище № 105»
Преподаватель математики
– Ковалевская Нина Мендельевна
Слайд 2СЕДЬМОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ
Раскрыть содержание таких важных понятий как логарифм, логарифмическая
функция, логарифмическое уравнение, логарифмическое неравенство.
Обеспечить овладение практическими приемами преобразования выражений, содержащих логарифмы, построения графика логарифмической функции.
Сформировать навыки решения логарифмических уравнений и неравенств, характерных для программных требований.
ЛОГАРИФМЫ
Слайд 3 «Изобретение логарифмов, сокращая вычисления нескольких
месяцев в труд нескольких дней, словно удваивают жизнь астрономов».
Лаплас
СЕДЬМОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ
Слайд 9
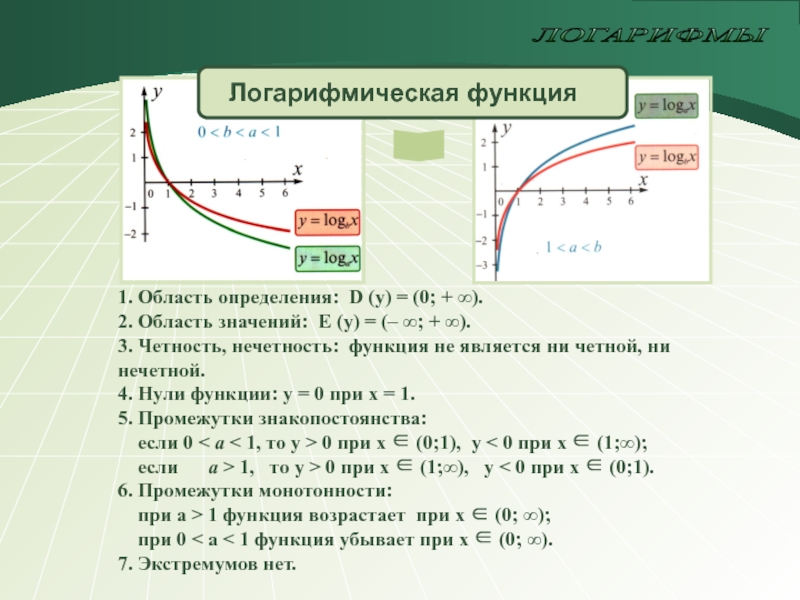
1. Область определения: D (y) = (0; + ∞).
2. Область значений:
E (y) = (– ∞; + ∞).
3. Четность, нечетность: функция не является ни четной, ни нечетной.
4. Нули функции: у = 0 при x = 1.
5. Промежутки знакопостоянства:
если 0 < a < 1, то у > 0 при х ∈ (0;1), у < 0 при х ∈ (1;∞);
если a > 1, то у > 0 при х ∈ (1;∞), у < 0 при х ∈ (0;1).
6. Промежутки монотонности:
при а > 1 функция возрастает при х ∈ (0; ∞);
при 0 < а < 1 функция убывает при х ∈ (0; ∞).
7. Экстремумов нет.
3. Четность, нечетность: функция не является ни четной, ни нечетной.
4. Нули функции: у = 0 при x = 1.
5. Промежутки знакопостоянства:
если 0 < a < 1, то у > 0 при х ∈ (0;1), у < 0 при х ∈ (1;∞);
если a > 1, то у > 0 при х ∈ (1;∞), у < 0 при х ∈ (0;1).
6. Промежутки монотонности:
при а > 1 функция возрастает при х ∈ (0; ∞);
при 0 < а < 1 функция убывает при х ∈ (0; ∞).
7. Экстремумов нет.
Слайд 11
Номера клавишей рояля представляют собой логарифмы чисел соответствующих звуков.
Номера октавы представляют
собой характеристику,
а номер звука в данной октаве – мантиссу этого логарифма.
Слайд 12Оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов, составленной при
основании 2,5.
Слайд 28«С точки зрения вычислительной практики, изобретение логарифмов по важности можно смело
поставить рядом с другим, более древним великим изобретением индусов – нашей десятичной системой нумерации».
Я.В. Успенский
СЕДЬМОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ
Слайд 29СЕДЬМОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ
Информационные источники
Математика: учебник для 11 класса: среднее (полное)
общее образование (базовый уровень) / М.И. Башмаков. – М.: Издательский центр «Академия», 2008.
Занимательная алгебра / Я.И. Перельман. – М: Издательство «Наука», 1976.
Занимательная алгебра / Я.И. Перельман. – М: Издательство «Наука», 1976.