Мария Ивановна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач по комбинаторике
Содержание
- 1. Решение задач по комбинаторике
- 2. Тема занятия«Комбинаторные задачи»Цель :-повторить способы решения комбинаторных задач;
- 3. Комбинаторика – раздел математики, в котором изучают
- 4. Способы решения комбинаторных задач Перебор возможных вариантов.
- 5. Перебор возможных вариантовСколько существует двухзначных чисел, составленных
- 6. Таблицей Алла, Бэла, Валентина и Галина во
- 7. Дерево возможных вариантовНикита, Борис, Виктор, и Григорий
- 8. Правило умноженияВ меню в столовой предложены на
- 9. Правило треугольникаВстретились 5 приятелей и обменялись рукопожатиями.
- 10. С помощью графовПо окончанию деловой встречи 4
- 11. Решите задачу несколькими способамиАндрей, Борис, Виктор и
- 12. Знаешь ли ты?Как прочитать и решить такой пример? 10!6!8!
- 13. Решить задачу.Сколькими способами 4 пассажира могут разместиться
- 14. Итог урока Домашнее задание6 решить задачи.Сколько различных
Тема занятия«Комбинаторные задачи»Цель :-повторить способы решения комбинаторных задач;
Слайд 3Комбинаторика – раздел математики, в котором изучают вопросы о том, сколько
различных комбинаций, подчинённых тем или иным условиям можно составить из данных объёктов. Выбором объектов и расположением их в том или ином порядке приходиться заниматься чуть ли не во всех областях человеческой деятельности. Например, конструктору, разрабатывающему новую модель механизма, учёному-агроному, планирующему сельхозкультуры на нескольких полях, химику, изучающему строение молекул.
С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. В Китае увлекались составлением магических квадратов, в Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов стихотворных размеров. Комбинаторные задачи возникли в связи с такими играми, как шашки, шахматы, карты, кости и др.Чтобы их решить, нужно было уметь подсчитывать число различных комбинаций, подчинённых тем или иным условиям.
С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. В Китае увлекались составлением магических квадратов, в Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов стихотворных размеров. Комбинаторные задачи возникли в связи с такими играми, как шашки, шахматы, карты, кости и др.Чтобы их решить, нужно было уметь подсчитывать число различных комбинаций, подчинённых тем или иным условиям.
Слайд 4Способы решения комбинаторных задач
Перебор возможных вариантов.
Таблицей.
Дерево возможных вариантов.
Правило
умножения.
Правило треугольника.
С помощью графов.
Правило треугольника.
С помощью графов.
Слайд 5Перебор возможных вариантов
Сколько существует двухзначных чисел, составленных из цифр: 0, 5,
8 ?
Решение.
58, 50, 80, 85.
Ответ: 4 числа.
Решение.
58, 50, 80, 85.
Ответ: 4 числа.
Слайд 6Таблицей
Алла, Бэла, Валентина и Галина во время майского праздника подарили
друг другу по одному цветку. Причём каждая девочка подарила каждой по одному цветку. Сколько всего цветков было подарено?
Решение.
Ответ: 12
цветков.
Решение.
Ответ: 12
цветков.
Слайд 7Дерево возможных вариантов
Никита, Борис, Виктор, и Григорий играли в шахматы. Каждый
сыграл по 1 партии. Сколько сыграно партий?
Решение.
Никита
Борис Виктор Григорий
Виктор Григорий Григорий
Ответ. 6 партий.
Решение.
Никита
Борис Виктор Григорий
Виктор Григорий Григорий
Ответ. 6 партий.
Слайд 8Правило умножения
В меню в столовой предложены на выбор 3 первых блюда,
5 вторых и 4 третьих блюд. Сколько различных вариантов обедов, состоящих из 1 первого, 1 второго и 1 третьего блюда, можно составить из предложенного меню?
Решение.
3*5*4=60
Ответ: 60 блюд.
Решение.
3*5*4=60
Ответ: 60 блюд.
Слайд 9Правило треугольника
Встретились 5 приятелей и обменялись рукопожатиями. Сколько всего сделано рукопожатий?
Решение.
1 2 3 4 5
1 - + + + +
2 - - + + +
3 - - - + +
4 - - - - +
5 - - - - - Ответ: 10 рукопожатий.
1 - + + + +
2 - - + + +
3 - - - + +
4 - - - - +
5 - - - - - Ответ: 10 рукопожатий.
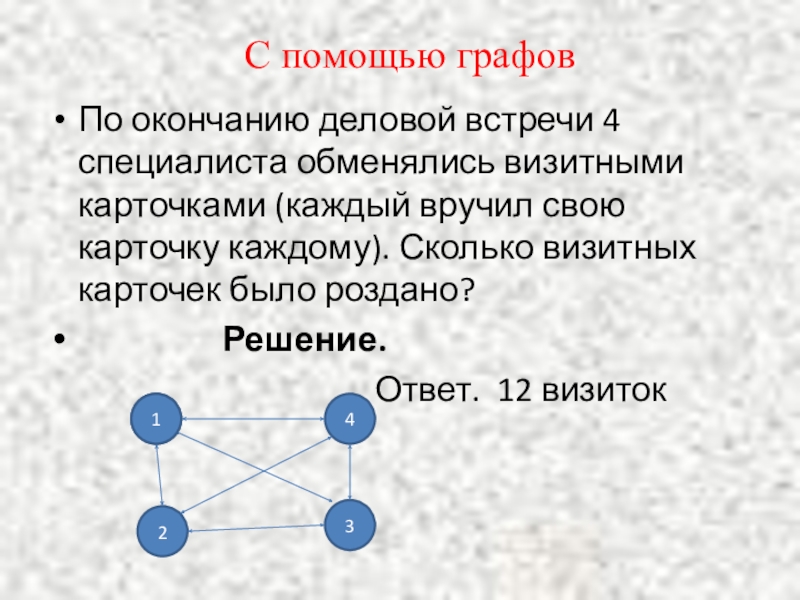
Слайд 10С помощью графов
По окончанию деловой встречи 4 специалиста обменялись визитными карточками
(каждый вручил свою карточку каждому). Сколько визитных карточек было роздано?
Решение.
Ответ. 12 визиток
Решение.
Ответ. 12 визиток
1
2
4
3
1
Слайд 11Решите задачу несколькими способами
Андрей, Борис, Виктор и Григорий после возвращения из
спортивного лагеря подарили друг другу на память свои фотографии. Причём каждый мальчик подарил каждому по 1 фотографии. Сколько всего фотографий было подарено?
Слайд 13Решить задачу.
Сколькими способами 4 пассажира могут разместиться в четырёхместном купе.
Сколькими способами
можно расположить 8 человек за круглым столом на восьми стульях.
Сколько открыток надо купить, чтобы 6 человек могли поздравит друг друга с праздником.
Сколько открыток надо купить, чтобы 6 человек могли поздравит друг друга с праздником.
Слайд 14Итог урока
Домашнее задание6 решить задачи.
Сколько различных трёхзначных чисел без повторения цифр
можно составить из цифр 1,2,3,4,5,6?
Двое размещаются в четырёхместном купе; каждый выбирает себе место. Сколькими способами они могут это сделать?.
Перечислить знакомые виды: 1) четырёхугольников; 2) треугольников.
Двое размещаются в четырёхместном купе; каждый выбирает себе место. Сколькими способами они могут это сделать?.
Перечислить знакомые виды: 1) четырёхугольников; 2) треугольников.