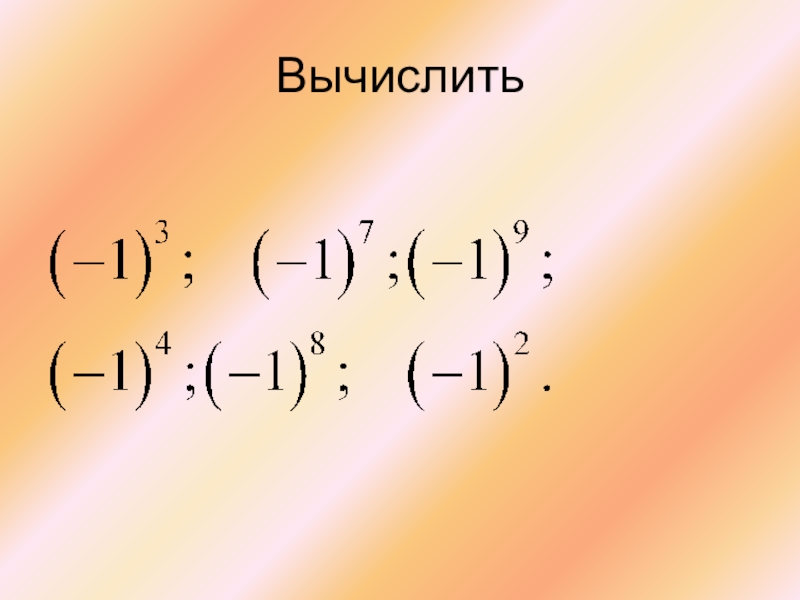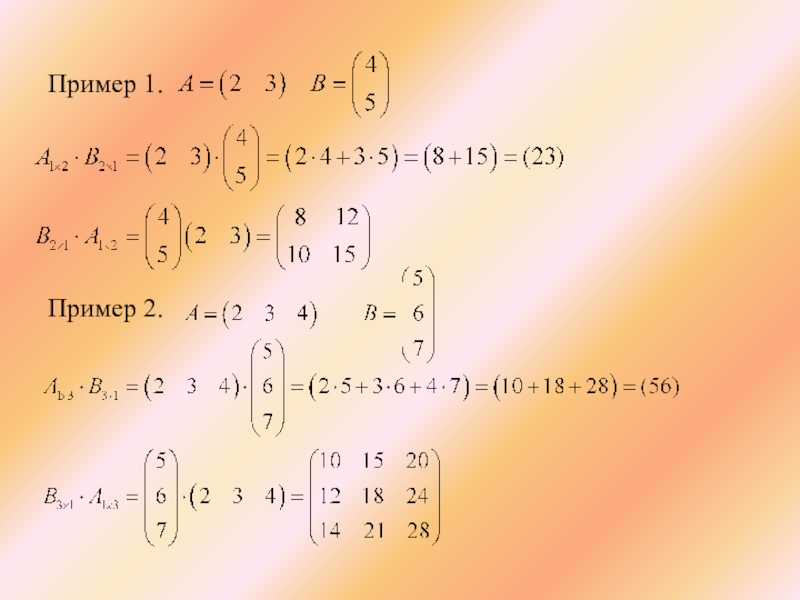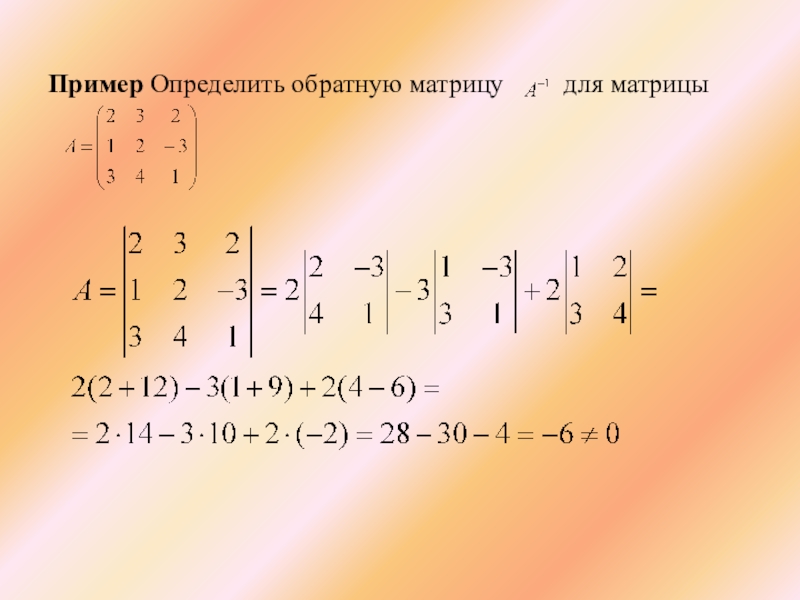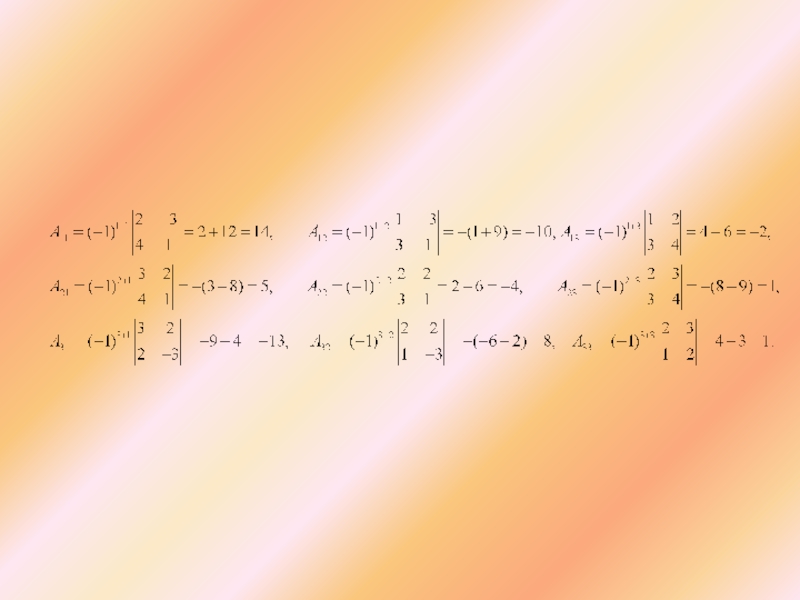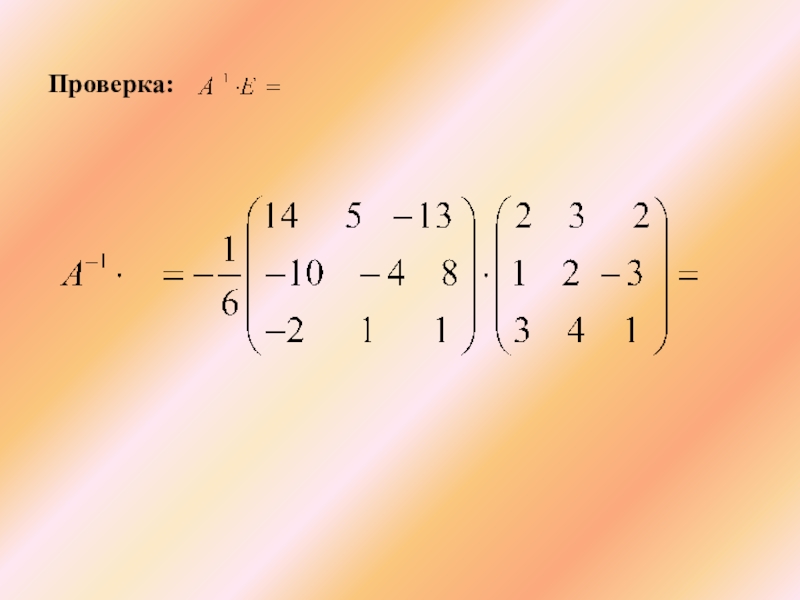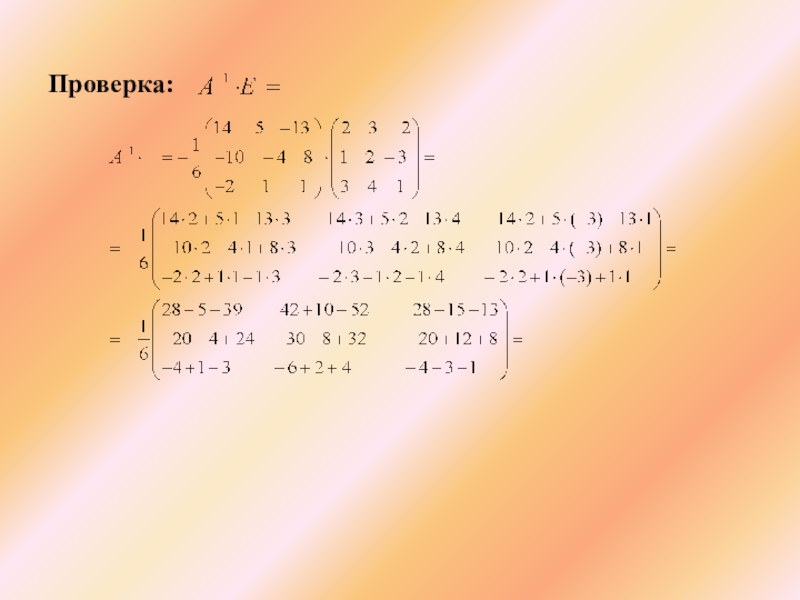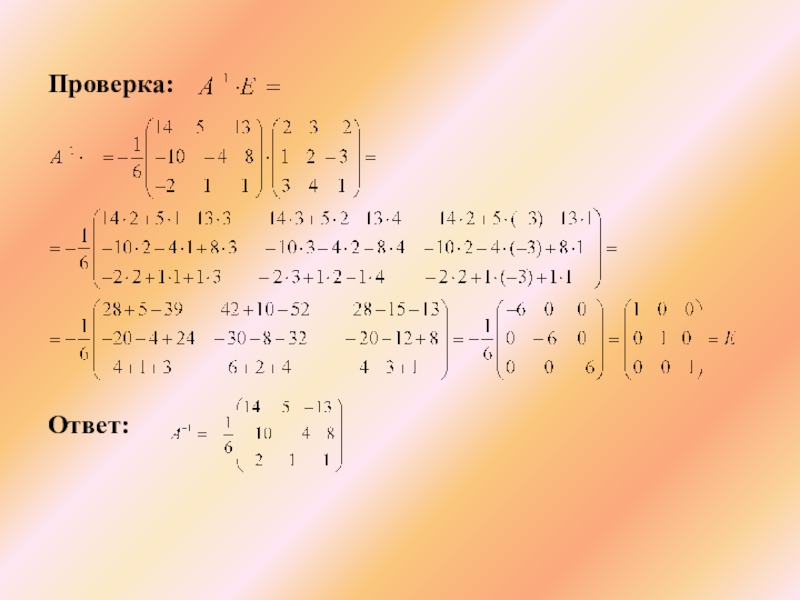- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение систем трех линейных уравнений матричным методом
Содержание
- 1. Решение систем трех линейных уравнений матричным методом
- 2. Слайд 2
- 3. Цели занятия:сформировать: - понятие о матрицах,
- 4. Математика является универсальным языком, который широко применяется
- 5. Историческая справка
- 6. Матрица, её история и применение Матрица — математический
- 7. План1. Определение обратной матрицы.2. Нахождение обратной матрицы.3.
- 8. Ключевые понятия и термины:матрица;определитель матрицы;квадратная матрица;прямоугольная матрица;виды матриц;обратная матрица;алгоритм нахождения обратной матрицы;алгебраические дополнения.
- 9. Литература 1. Алгебра и начала математического анализа:
- 10. Вопросы к темеЧто такое матрицы и
- 11. Актуализация опорных знаний студентовВопросы для фронтального опроса
- 12. Вычислить
- 13. Актуализация опорных знаний студентовВопросы для фронтального опроса
- 14. Актуализация опорных знаний студентовВопросы для фронтального опроса
- 15. 4. Проведем короткий анализ домашней работы. 5.
- 16. Изложение теоретического материала и его закрепление Изложение теоретического материала и его закрепление
- 17. 1. Матрица – это упорядоченная таблица чисел которая имеет m строк и n столбцов.
- 18. Числа это элементы матрицы. Следует
- 19. нулевая матрица размером
- 20. Равенство матриц Две матрицы с одинаковыми размерами
- 21. Транспонирование матрицы Если в данной матрице поменять
- 22. Где ещё применяются матрицы?Теперь подробнее остановимся на
- 23. Данная таблица может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
- 24. В данной записи, например, матричный элемент показывает,
- 25. Произведением двух матриц АВ является
- 26. Свойства произведений матриц
- 27. Пример 1. Пример 2.
- 28. Пример 3.
- 29. 2. Обратная матрица. Матрицей
- 30. - определитель матрицы
- 31. Матрицы можно подвергать элементарным преобразованиям:1. Можно менять
- 32. Пример1. Определить обратную матрицу Нахождение обратной матрицыПример1.
- 33. Пример1. Определить обратную матрицу Нахождение обратной матрицыПример1.
- 34. Проверка правильности вычислений:
- 35. Пример Определить обратную матрицу для матрицы
- 36. Пример Определить обратную матрицу для матрицы
- 37. Пример Определить обратную матрицу для матрицы
- 38. Пример Определить обратную матрицу для матрицы
- 39. Пример Определить обратную матрицу для матрицы
- 40. Пример Определить обратную матрицу для матрицы
- 41. Пример Определить обратную матрицу для матрицы
- 42. Слайд 42
- 43. Пример Определить обратную матрицу
- 44. Проверка:
- 45. Проверка:
- 46. Проверка: Ответ:
- 47. 3. Решение система трех линейных уравнений
- 48. Пример 1. Решить систему трех линейных уравнений
- 49. Теперь будем находить алгебраические дополнения:
- 50. Теперь будем находить алгебраические дополнения:
- 51. Теперь будем находить алгебраические дополнения:
- 52. Теперь будем находить алгебраические дополнения:
- 53. Теперь будем находить алгебраические дополнения:
- 54. Так как
- 55. Так как
- 56. Так как
- 57. Так как
- 58. Подведение итогов занятия. Благодарю за работу на занятии.
Цели занятия:сформировать: - понятие о матрицах, их видах, действиях над ними; - о матричным методом методе решения системы трех линейных уравнений с тремя переменными;воспитывать стремление к познанию, внимательное отношение к делу, аккуратность, самостоятельность, творческое
Слайд 3
Цели занятия:
сформировать:
- понятие о матрицах, их видах, действиях над
ними;
- о матричным методом методе решения системы трех линейных уравнений с тремя переменными;
воспитывать стремление к познанию, внимательное отношение к делу, аккуратность, самостоятельность, творческое отношение к учебной деятельности;
развивать логическое и аналитическое мышление; прививать интерес к поисковой деятельности.
- о матричным методом методе решения системы трех линейных уравнений с тремя переменными;
воспитывать стремление к познанию, внимательное отношение к делу, аккуратность, самостоятельность, творческое отношение к учебной деятельности;
развивать логическое и аналитическое мышление; прививать интерес к поисковой деятельности.
Слайд 4
Математика является универсальным языком, который широко применяется во всех сферах человеческой
деятельности.
Во многих экономических и профессиональных дисциплинах необходимы знания о матрицах, операциях над ними, умения решать прикладные задачи с помощью матриц.
Актуальность этой темы усиливается в связи
с широким использованием матриц в экономических дисциплинах: финансы, экономика предприятий, статистика, логистика, экономико – математическое моделирование и др.
Во многих экономических и профессиональных дисциплинах необходимы знания о матрицах, операциях над ними, умения решать прикладные задачи с помощью матриц.
Актуальность этой темы усиливается в связи
с широким использованием матриц в экономических дисциплинах: финансы, экономика предприятий, статистика, логистика, экономико – математическое моделирование и др.
Слайд 6Матрица, её история и применение
Матрица — математический объект, записываемый в виде
прямоугольной
таблицы элементов, которая представляет
собой совокупность строк и столбцов, на пересечении
которых находятся её элементы. Количество строк и
столбцов матрицы задают размер матрицы. Термин «матрица» имеет много значений. Матрица — (нем., Matrize, от лат. matrix матка). 1) в литейном производстве: медная форма для отливки букв, а также монет. 2) в типографском деле: бумажная форма для отливки стереотипа. В программировании матрица – это двумерный массив, в электронике – набор проводников, которые можно замкнуть в точках их пересечений. Матрица в фотографии – это интегральная микросхема, которая состоит из фотодиодов (светочувствительных элементов).
собой совокупность строк и столбцов, на пересечении
которых находятся её элементы. Количество строк и
столбцов матрицы задают размер матрицы. Термин «матрица» имеет много значений. Матрица — (нем., Matrize, от лат. matrix матка). 1) в литейном производстве: медная форма для отливки букв, а также монет. 2) в типографском деле: бумажная форма для отливки стереотипа. В программировании матрица – это двумерный массив, в электронике – набор проводников, которые можно замкнуть в точках их пересечений. Матрица в фотографии – это интегральная микросхема, которая состоит из фотодиодов (светочувствительных элементов).
Слайд 7План
1. Определение обратной матрицы.
2. Нахождение обратной матрицы.
3. Решение системы трех линейных
уравнений с тремя неизвестными методом обратной матрицы.
Слайд 8Ключевые понятия и термины:
матрица;
определитель матрицы;
квадратная матрица;
прямоугольная матрица;
виды матриц;
обратная матрица;
алгоритм нахождения обратной
матрицы;
алгебраические дополнения.
алгебраические дополнения.
Слайд 9Литература
1. Алгебра и начала математического анализа: учебник для общеобразоват. организаций:
базов. и углубл. уровни / Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др. – М.: Просвещение, 2016. – 463 с.
2. Высшая математика для экономистов: Учебное пособие. – К.: Знания, Макаренко В.А., 2008 – 517 с.
3. Математика: Учебник / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
4.Дидактический материал по математике: Учебное пособие / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
5. Практические занятия по математике. Н.В. Богомолов. – М.: Высшая школа, 1983.
2. Высшая математика для экономистов: Учебное пособие. – К.: Знания, Макаренко В.А., 2008 – 517 с.
3. Математика: Учебник / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
4.Дидактический материал по математике: Учебное пособие / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
5. Практические занятия по математике. Н.В. Богомолов. – М.: Высшая школа, 1983.
Слайд 10
Вопросы к теме
Что такое матрицы и зачем они нужны? Какие
виды матриц существуют?
Как найти определитель матрицы?
Какие операции можно выполнять над матрицами?
Какая матрица называется обратной?
Как найти обратную матрицу?
Как решить систему трех линейных уравнений с тремя переменными методом обратной матрицы?
Как найти определитель матрицы?
Какие операции можно выполнять над матрицами?
Какая матрица называется обратной?
Как найти обратную матрицу?
Как решить систему трех линейных уравнений с тремя переменными методом обратной матрицы?
Слайд 11Актуализация опорных знаний студентов
Вопросы для фронтального опроса студентов
1. Как вычисляется определитель
второго порядка?
2. Вычислить определитель второго порядка:
2. Вычислить определитель второго порядка:
Слайд 13Актуализация опорных знаний студентов
Вопросы для фронтального опроса студентов
1. Как вычисляется определитель
второго порядка?
2. Вычислить определитель второго порядка:
3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
2. Вычислить определитель второго порядка:
3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
Слайд 14Актуализация опорных знаний студентов
Вопросы для фронтального опроса студентов
1. Как вычисляется определитель
второго порядка?
2. Вычислить определитель второго порядка:
3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
2. Вычислить определитель второго порядка:
3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
Слайд 15
4. Проведем короткий анализ домашней работы.
5. Проверить определитель второго порядка
из домашнего задания
6. Проверить определитель третьего порядка из домашнего задания
6. Проверить определитель третьего порядка из домашнего задания
Слайд 16Изложение теоретического материала
и его закрепление
Изложение теоретического материала
и его
закрепление
Слайд 18 Числа это элементы матрицы. Следует помнить, что определитель – это
величина, которую изображают в виде квадратной таблицы; матрица – это всегда таблица чисел, никак по-другому не определяема.
Если , то матрица прямоугольная, если , то –
квадратная.
прямоугольная матрица размером
квадратная матрица ІІ порядка.
диагональная матрица ІІІ порядка.
Слайд 20Равенство матриц
Две матрицы с одинаковыми размерами
равны, если
их соответствующие элементы равны:
и , то A=B,
их соответствующие элементы равны:
и , то A=B,
Так если
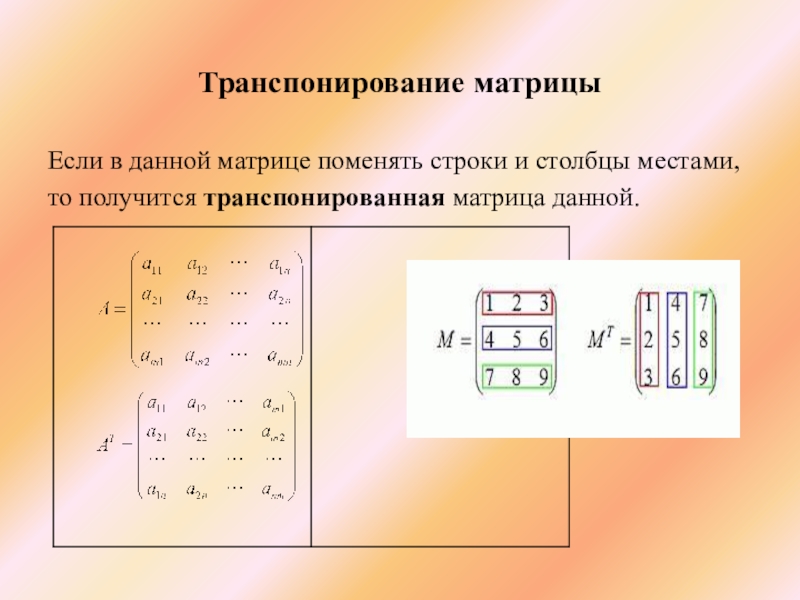
Слайд 21Транспонирование матрицы
Если в данной матрице поменять строки и столбцы местами,
то получится транспонированная матрица данной.
Слайд 22
Где ещё применяются матрицы?
Теперь подробнее остановимся на некоторых областях применения матриц.
Понятие
матрицы и основанный на нем раздел математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов.
Так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме.
С помощью матриц удобно записывать некоторые экономические зависимости.
Так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме.
С помощью матриц удобно записывать некоторые экономические зависимости.
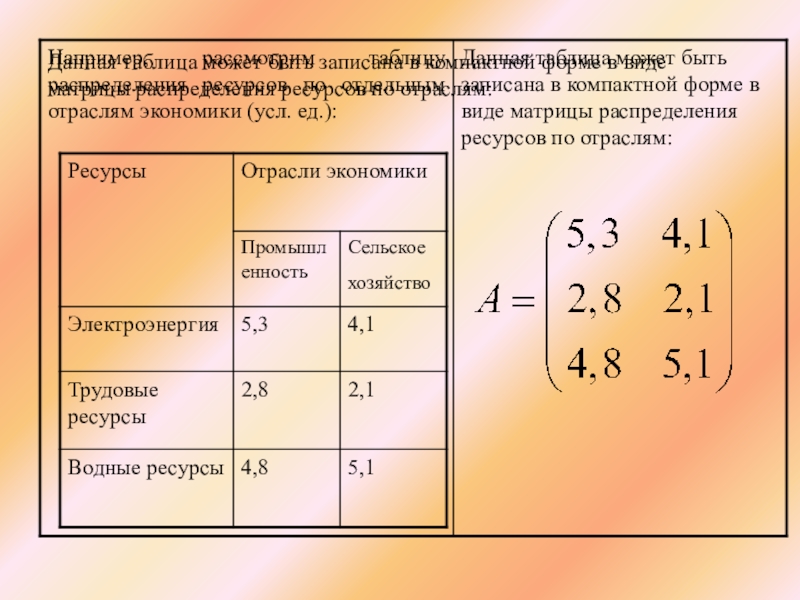
Слайд 23Данная таблица может быть записана в компактной форме в виде матрицы
распределения ресурсов по отраслям:
Слайд 24
В данной записи, например, матричный элемент показывает, сколько электроэнергии употребляет промышленность,
а элемент - сколько трудовых ресурсов потребляет сельское хозяйство.
С помощью матриц можно решать системы уравнений, в них удобно представлять какие-либо данные.
Таким образом, мы пришли к выводу, что матрицы широко применялись и применяются до сих пор.
С помощью матриц можно решать системы уравнений, в них удобно представлять какие-либо данные.
Таким образом, мы пришли к выводу, что матрицы широко применялись и применяются до сих пор.
Слайд 25
Произведением двух матриц АВ является матрица С, элемент
которой равен сумме произведений соответствующих элементов i - той строки матрицы А и j - того столбца матрицы В. (Чтобы получить i-тую строку произведения, необходимо умножить i-тую строку матрицы А на каждый столбец матрицы В)
Чтобы умножать матрицы, необходимо, чтобы количество столбцов матрицы А было равно количеству строк матрицы В.
Размер А: m×n; размер В: n×p, то размер АВ: m×p.
Чтобы умножать матрицы, необходимо, чтобы количество столбцов матрицы А было равно количеству строк матрицы В.
Размер А: m×n; размер В: n×p, то размер АВ: m×p.
Слайд 292. Обратная матрица.
Матрицей называют обратной
к квадратной матрице А, если произведение этих матриц равняется единичной матрицей, то есть
Обратная матрица существует для всякой невырожденной квадратной матрицы А, то есть когда определитель матрицы
Обратная матрица невырожденной квадратной матрицы А находится по формуле:
- определитель матрицы А, - алгебраические дополнения элементов определителя
Обратная матрица существует для всякой невырожденной квадратной матрицы А, то есть когда определитель матрицы
Обратная матрица невырожденной квадратной матрицы А находится по формуле:
- определитель матрицы А, - алгебраические дополнения элементов определителя
.
Слайд 30
- определитель матрицы А,
- алгебраические дополнения элементов определителя
Запишем алгоритм нахождения обратной матрицы для квадратной матрицы А:
1) вычислить определитель матрицы А. Если , то матрица А имеет обратную, в противном случае обратной матрицы не существует;
2) вычислить алгебраические дополнения элементов матрицы А;
3) Записать обратную матрицу
4) проверить правильность вычислений:
Алгебраические дополнения в обратной матрице записываются не по строкам, а по столбцам.
Запишем алгоритм нахождения обратной матрицы для квадратной матрицы А:
1) вычислить определитель матрицы А. Если , то матрица А имеет обратную, в противном случае обратной матрицы не существует;
2) вычислить алгебраические дополнения элементов матрицы А;
3) Записать обратную матрицу
4) проверить правильность вычислений:
Алгебраические дополнения в обратной матрице записываются не по строкам, а по столбцам.
Слайд 31
Матрицы можно подвергать элементарным преобразованиям:
1. Можно менять местами строки и столбцы.
2. Можно строку (столбец) умножать на одно и то же число.
3. К некоторой строке или столбцу можно прибавить другую строку (столбец), умноженную на некоторое число.
Такие преобразования приводят к замене строк или столбцов строками (столбцами), состоящими из нулей, которые надо удалять из матрицы для рассмотрения матрицы меньшего размера.
Слайд 32Пример1. Определить обратную матрицу
Нахождение обратной матрицы
Пример1. Определить обратную матрицу
для
матрицы
Решение. Вычислим определитель матрицы А:
то для матрицы А существует обратная матрица .
Запишем алгебраические дополнения элементов матрицы А:
Слайд 33Пример1. Определить обратную матрицу
Нахождение обратной матрицы
Пример1. Определить обратную матрицу
для
матрицы
Решение. Вычислим определитель матрицы А:
то для матрицы А существует обратная матрица .
Запишем алгебраические дополнения элементов матрицы А:
Слайд 34Проверка правильности вычислений:
(Сделать вывод. Для матриц А и справедлив переместительный закон умножения).
Делаем вывод. Для матриц А и справедлив переместительный закон умножения.
Ответ:
Делаем вывод. Для матриц А и справедлив переместительный закон умножения.
Ответ:
Слайд 43Пример Определить обратную матрицу для матрицы
Решение.
Вычислим определитель матрицы А:
то для матрицы А существует обратная матрица
Запишем алгебраические дополнения элементов матрицы А:
Обратная матрица имеет вид:
то для матрицы А существует обратная матрица
Запишем алгебраические дополнения элементов матрицы А:
Обратная матрица имеет вид:
Слайд 47 3. Решение система трех линейных уравнений с тремя неизвестными методом
обратной матрицы
Пусть задана система трех линейных уравнений с тремя неизвестными
Если основная матрица системы линейных уравнений
является квадратной и невырожденной, то систему можно решить матричным способом (с помощью обратной матрицы). Записав систему в матричном виде, получим решение X системы уравнений:
А- матрица, составленная из коэффициентов при переменных x. y. z .
Х- матрица – столбец составленная из переменных величин.
В- матрица – столбец составленная из свободных членов.
Слайд 48Пример 1. Решить систему трех линейных уравнений с тремя неизвестными методом
обратной матрицы:
Решение. Запишем систему в матричном виде , где
Решение матричного уравнения будет иметь вид:
Найдем обратную матрицу
Сначала найдем главный определитель матрицы:
Слайд 58Подведение итогов занятия.
Благодарю за работу на занятии.
Подсчитываем поощрительные баллы.
Оценки
комментируются и выставляются в журнал.
