- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение экономических задач
Содержание
- 1. Решение экономических задач
- 2. Цель работы:
- 3. Актуальность: Решение «экономических» задач
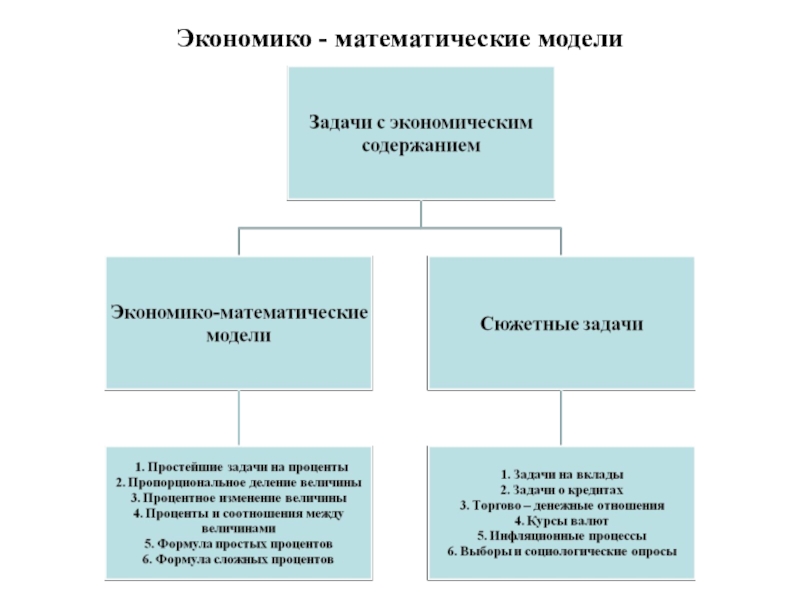
- 4. Экономико - математические модели
- 5. Порядок действий
- 6. Слайд 6
- 7. Для подсчета величины в скобках иногда применяется
- 8. 3. Типы экономических
- 9. Вычисление процентной ставки по кредиту неизвестно
- 10. 3.3. Нахождение периодической выплаты банку (транша) По
- 11. 3. 4. Нахождение суммы кредита По
- 12. Нестандартные экономические задачиЗадача 7. Предприниматель купил здание
- 13. Заключение Я считаю введение таких задач
- 14. Благодарю за внимание!
Слайд 1Министерство образования и науки Республики Бурятия
МБОУ «Белоозерская СОШ»
Научно-практическая конференция
«Шаг в будущее»
Тема:
««Решение задач с экономическим содержанием»»
Выполнил: Шахметов Игорь
ученик 10 класса Белоозерской СОШ
Руководитель: Ишеева Д-Х. Г
учитель математики
2017г
Слайд 2 Цель работы:
Разработать алгоритм решения
Задачи:
Изучить теоретические аспекты решения «экономических» задач;
Познакомиться с видами «экономических" задач из сборников для подготовки к ЕГЭ 2017 г. и открытого банка задач по математике;
Рассмотреть разные типы заданий ЕГЭ под №17 и их способы решения.
Слайд 3 Актуальность: Решение «экономических» задач представлены в школьном курсе математики
Объект:
«Экономические» задачи на проценты повышенного уровня сложности
Методы исследования:
поисковый метод с использованием научной и учебной литературы, интернета;
исследовательский метод при определении видов задач, их решения различными способами;
анализ полученных в ходе исследования данных.
Слайд 5Порядок действий
процент банка p,
ежегодная выплата по кредиту K
Формулы для подсчета процентов:
а) если величину S увеличить на p% получится S∙(1+p/100);
б) если величину S уменьшить на p% получим S∙(1-p/100);
в) если величину S дважды увеличить на p% получим S∙(1+p/100)²;
г) если величину S увеличивать на p% не два раза, а три раза, получится S∙(1+p/100)³;
д) если величину Х увеличивать на p% п раз, то степень пS∙(1+p/100)n.
Слайд 6
Если заемщик выплачивает
Через год после начисления процентов и выплаты суммы K,
размер долга равен S∙(1+p/100)-K.
Каждый год сумма будет умножаться на выражение в
скобках, введем замену переменных
Обозначим: Р=1+p/100, тогда S∙Р-K.
Через два года размер долга будет выглядеть следующим образом:
(SР-K)∙Р-K;
Через три года: ((SР-K)∙Р-K)∙Р-K;
Через четыре года: (((SР-K)∙Р-K)∙Р-K) Р-K;
Через n лет: SРⁿ-K(Рⁿ+ Рn-1+Рn-2+Р³+Р²+Р+1).
Слайд 7Для подсчета величины в скобках иногда применяется
Формула суммы
в В1 равен 1,
q равен Р
Формула для суммы п членов геометрической прогрессии:
Kn=
В нашем случае размер долга через n лет равен:
SРⁿ - K
Итак, мы видим в нашей формуле следующие четыре переменные:
размер денежной суммы - S
процент банка - p,
периодическая выплата банку (транш) – K
временной период происходящих действий (года, месяцы) – n
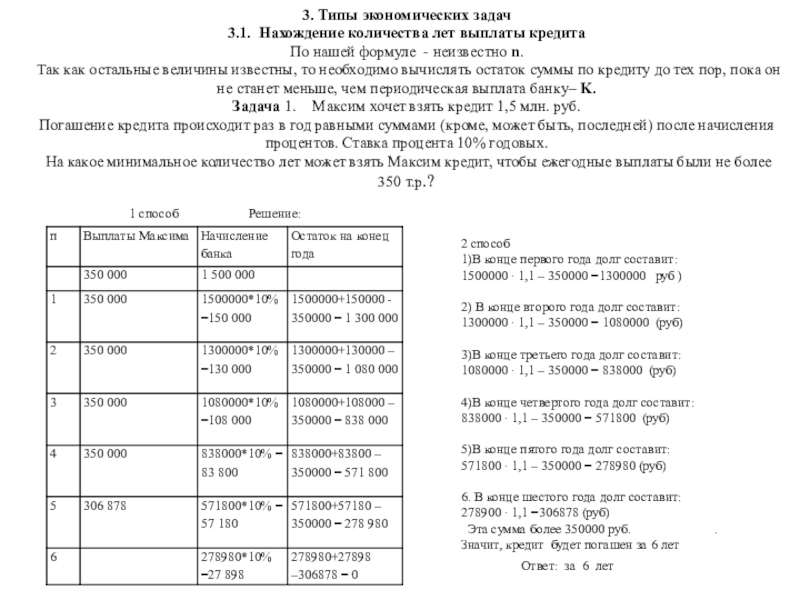
Слайд 8 3. Типы экономических задач 3.1. Нахождение количества лет выплаты кредита По нашей формуле
1 способ Решение:
2 способ
1)В конце первого года долг составит:
1500000 ∙ 1,1 – 350000 =1300000 руб )
2) В конце второго года долг составит:
1300000 ∙ 1,1 – 350000 = 1080000 (руб)
3)В конце третьего года долг составит:
1080000 ∙ 1,1 – 350000 = 838000 (руб)
4)В конце четвертого года долг составит: 838000 ∙ 1,1 – 350000 = 571800 (руб)
5)В конце пятого года долг составит:
571800 ∙ 1,1 – 350000 = 278980 (руб)
6. В конце шестого года долг составит:
278900 ∙ 1,1 =306878 (руб)
Эта сумма более 350000 руб. .
Значит, кредит будет погашен за 6 лет
Ответ: за 6 лет
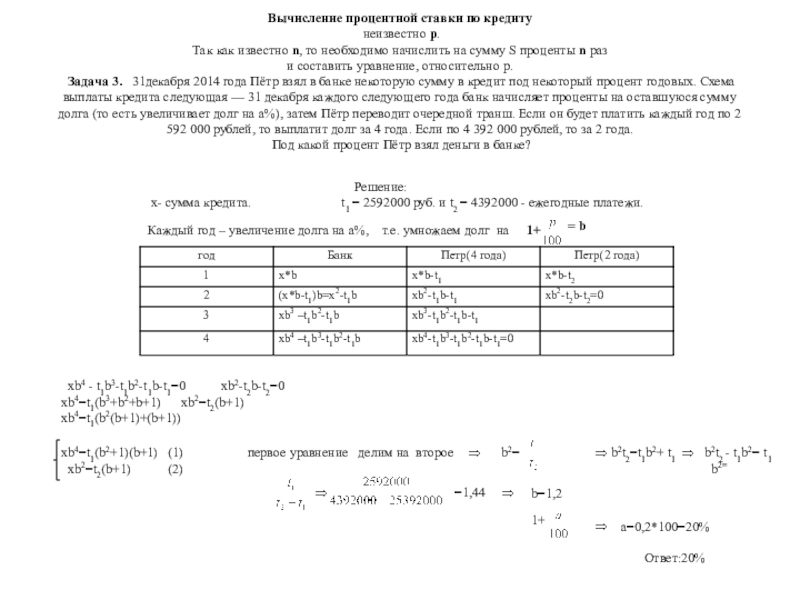
Слайд 9Вычисление процентной ставки по кредиту неизвестно p. Так как известно n, то
Решение:
х- сумма кредита. t1 = 2592000 руб. и t2 = 4392000 - ежегодные платежи.
Каждый год – увеличение долга на а%, т.е. умножаем долг на 1+
= b
xb4 - t1b3-t1b2-t1b-t1=0 xb2-t2b-t2=0
xb4=t1(b3+b2+b+1) xb2=t2(b+1)
xb4=t1(b2(b+1)+(b+1))
xb4=t1(b2+1)(b+1)
xb4=t1(b2+1)(b+1) (1) первое уравнение делим на второе
xb2=t2(b+1) (2)
b2=
(b2+1)
b2t2=t1b2+ t1
b2t2 - t1b2= t1
b2=
b2=
=1,44
b=1,2
1+
=1,2
а=0,2*100=20%
Ответ:20%
Слайд 103.3. Нахождение периодической выплаты банку (транша) По нашей формуле – неизвестно К. Составить
Решение:
Сергей взял в банке -х руб. (х=9930000 руб.)
Ежегодный платеж Сергея – а 1+
Ежегодное увеличение долга=10%, т. е. увеличивается в 1,1 раза (1+
=1,1),
Сергей уменьшает долг на а рублей.
Через 3 года полное погашение кредита: 1,331х-3,31а=0 (х=9930000 руб.)
а =
=3993000 рублей
Ответ: 3993000 рублей
Слайд 113. 4. Нахождение суммы кредита По нашей формуле – неизвестно S.
Задача 5.
31 декабря 2014 года Максим взял в банке некоторую сумму денег в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами, то есть за 4 года?
Решение:
Пусть S – сумма кредита.
1)В конце первого года долг составит: (1,1х – 2928200) рублей
2) В конце второго года долг (в рублях) составит: (1,1х – 2928200)∙1,1 – 2928200 = 1,21х – 3221020 – 2928200 = 1,21х – 6149220
3) В конце третьего года долг (в рублях) составит: (1,21х – 6149220)∙1,1 – 2928200 = 1,331х – 6764142 – 2928200 = =1,331х – 9692342
4) В конце четвертого года долг (в рублях) составит 2928200 рублей: (1,331х – 9692342)∙1,1 = 2928200; 1,4641х – 10661576 = 2928200; 1,4641х = 13589776; х = 9281999,8
Значит, сумма кредита равна 9282000 рублей.
Ответ: 9282000 рублей.
Слайд 12Нестандартные экономические задачи
Задача 7.
Предприниматель купил здание и собирается открыть в
Решение:
Пусть стандартных номеров –х, а номеров «люкс» -у.
Тогда общая площадь будет: 21х+49у=1099 кв. метров.
В сутки можно заработать: 2000х+4500у рублей и эта сумма должна быть наибольшей.
Из первого уравнения выразим у и подставим в выражение 2000х+4500у.
получим функцию заработанных в сутки денег: f(x)=2000х+4500∙
.
После преобразований получим: f(x)=
Она должна принимать наибольшее значение.
Так как х и у –натуральные числа, и функция f(x)- возрастающая, то она принимает наибольшее значение при наибольшем значении х.
будет целым, если х=50,
тогда f(x) =
= 104500 (рублей).
Легко заметить, что выражение
тогда f(x) =
Ответ: 104 500 рублей в сутки сможет заработать предприниматель на своем отеле