- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Разработка урока Касательная к графику функции
Содержание
- 1. Разработка урока Касательная к графику функции
- 2. Цели урока:Закрепить навыки работы с уравнением касательной
- 3. Тест по теме «Уравнение касательной к графику
- 4. 2. При каких значениях аргумента (отмеченных на
- 5. Слайд 5
- 6. 4.Дан график функции у = f (x)
- 7. Ответы:1. а) В; б) С;
- 8. На параболе y=x²-2x-8 найти точку М, в которой касательная к ней параллельна прямой 4x+y+4=0
- 9. 1) Найти угловой коэффициент k касательной, он
- 10. 1) 4х+у+4=0У=-4х-4⇒ k=42) f(х)=х²-2х -8f`(х)=2х-23)Приравняем к угловому коэффициенту данной прямой.2х-2=-42х=-4+22х=-2Х=-1-это абсцисса точки касанияУ=(-1)²-2(-1)-8=-5Ответ: точка М(-1:-5)Решение
- 11. Задача 4.169 Является ли прямая у =
- 12. С графиками функций в ногу я иду!Куда
Слайд 2Цели урока:
Закрепить навыки работы с уравнением касательной к графику функции.
Проверить навыки
Рассмотреть более сложные примеры по теме.
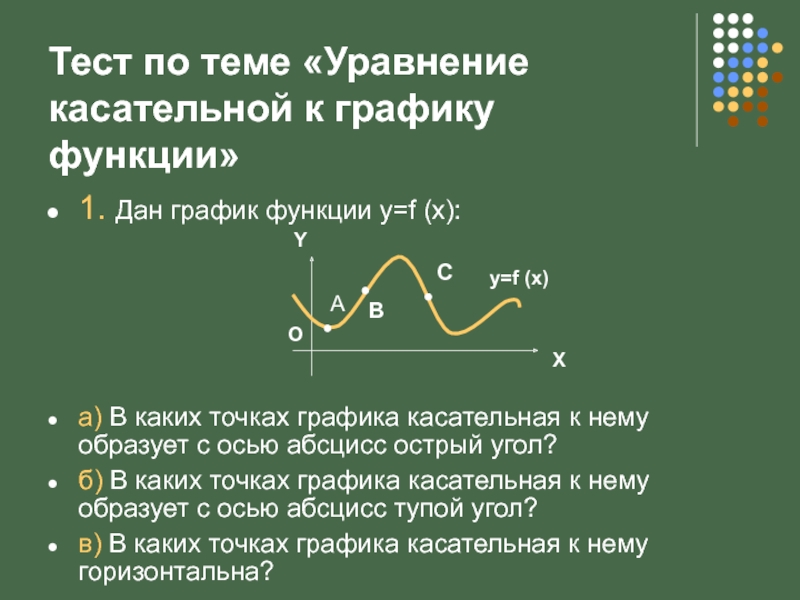
Слайд 3Тест по теме «Уравнение касательной к графику функции»
1. Дан график функции
а) В каких точках графика касательная к нему образует с осью абсцисс острый угол?
б) В каких точках графика касательная к нему образует с осью абсцисс тупой угол?
в) В каких точках графика касательная к нему горизонтальна?
X
O
Y
y=f (x)
А
В
С
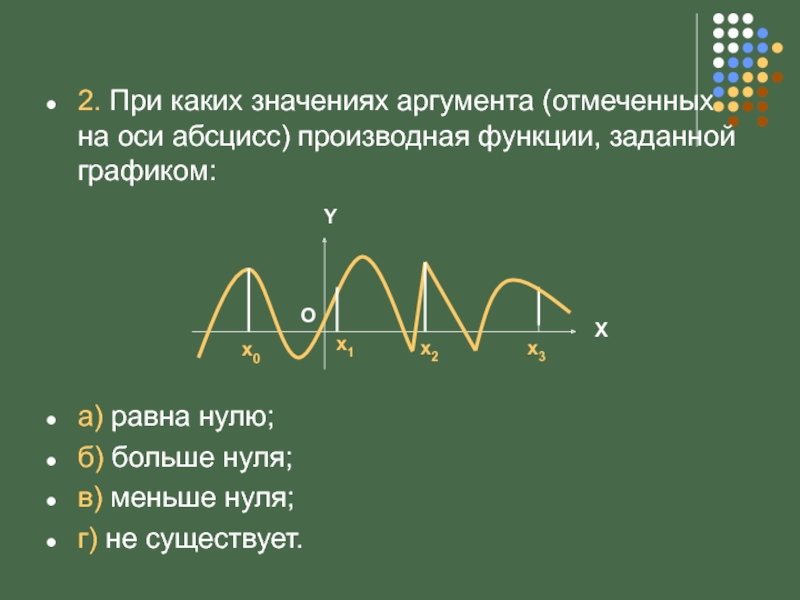
Слайд 42. При каких значениях аргумента (отмеченных на оси абсцисс) производная функции,
а) равна нулю;
б) больше нуля;
в) меньше нуля;
г) не существует.
Y
x0
x1
x2
x3
X
O
Слайд 5 3.Найдите угол наклона касательной к графику функции f (x) = 2x2,
а) π/6;
б) 3 π/4;
в) π /3;
г) π /4.
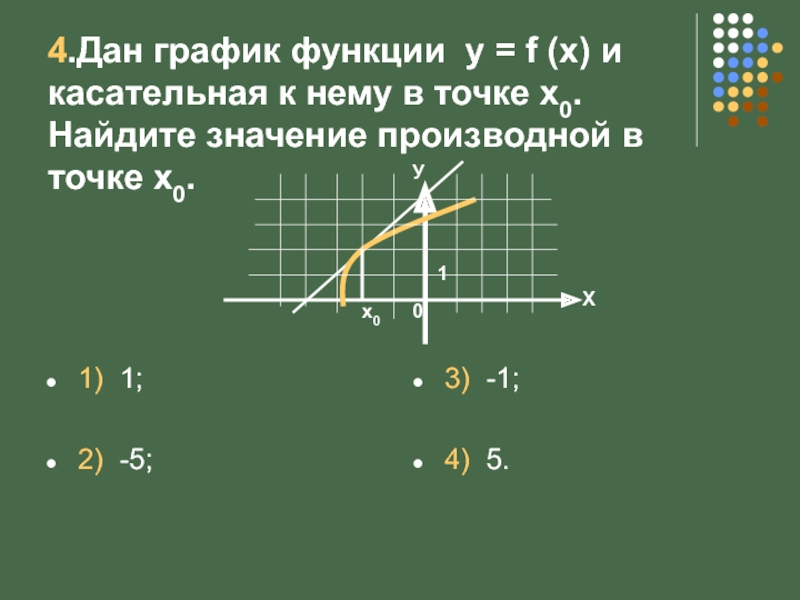
Слайд 64.Дан график функции у = f (x) и касательная к нему
1) 1;
2) -5;
3) -1;
4) 5.
Х
У
х0
0
1
Слайд 91) Найти угловой коэффициент k касательной, он равен угловому коэффициенту данной
2)Найти f`(х) для данной функции.
f`(х)= k-это угловой коэффициент касательной.
3)Приравнять к угловому коэффициенту прямой.
Схема решения
Слайд 101) 4х+у+4=0
У=-4х-4⇒ k=4
2) f(х)=х²-2х -8
f`(х)=2х-2
3)Приравняем к угловому коэффициенту данной прямой.
2х-2=-4
2х=-4+2
2х=-2
Х=-1-это абсцисса
У=(-1)²-2(-1)-8=-5
Ответ: точка М(-1:-5)
Решение
Слайд 11Задача 4.169 Является ли прямая у = 12х + 10 касательной к
Решение:
у = 12х + 10 ⇒ k = 12 – угловой коэффициент данной прямой.
у‘ = 12х2 – производная данной функции.
12х2 = 12 ⇒ х1,2 = ±1 – абсциссы точек касания, в которых угловой коэффициент касательной равен 12.
у = 12х – 8 – уравнение касательной в точке с абсциссой х0 = 1.
у = 12х + 8 – уравнение касательной в точке с абсциссой х0 = -1.
Ответ: Не является.
Слайд 12С графиками функций в ногу я иду!
Куда они укажут – туда
Ну, где тут производная? Где тангенс, наконец?
Да всё одно и тоже – мой угловой коэффициент!