- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Расстояние между скрещивающимися прямыми
Содержание
- 1. Расстояние между скрещивающимися прямыми
- 2. Основные понятия Расстоянием между скрещивающимися прямыми называется
- 3. В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми BA1 и DB1.хyz Точки
- 4. Решим систему из условия перпендикулярности двух векторов
- 5. В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми BA1 и DB1.
- 6. В правильной треугольной призме АВСА1В1С1, все ребра
- 7. Рассмотрим ∆АВС в плоскости ОХУxyACBH∆ ABC
- 8. В правильной четырехугольной пирамидеSABCD, сторона основания
- 9. MKA= (- 1/3)D, B=(1/3)D, C=(-1/4)D.Уравнение плоскости (МКD):
Слайд 1РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Координатным и векторным способом
Алферова Наталья Васильевна,
учитель математики
МКОУ «Горячеключевская СОШ»
Омского района Омской области
Слайд 2Основные понятия
Расстоянием между скрещивающимися прямыми называется длина общего перпендикуляра к
Расстоянием между скрещивающимися прямыми называется расстояние от точки одной прямой до плоскости параллельной данной прямой и содержащей вторую прямую.
Слайд 3В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми BA1 и DB1.
х
y
z
Точки A1 (1;0;1), B (1;1;0)
Вектор A1B {0;1;-1}
Точки D (0;0;0), B1 (1;1;1)
Вектор DB1 {1;1;1}
Пусть КМ ┴А1В и КМ┴DВ1, значит КМ – искомое расстояние.
Пусть точка К лежит на прямой A1B, а точка М на прямой DB1. Рассмотрим векторы А1К и DM, сонаправленные с направляющими векторами данных прямых . По лемме о коллинеарных векторах вектор А1К = а · А1В, т.е. вектор А1К{0;a;-a}, вектор DM = b · DB1, т.е. вектор DM {b;b;b}.
Тогда К(1;а;1-а), М(b;b;b) и вектор КМ {b-1;b-a;b-1+a}.
К
М
Слайд 4Решим систему из условия перпендикулярности двух векторов
KM·A1B=0
KM·DB1=0 1·(b-1)+1·(b-a)+1·(b-1+a) = 0
Решив систему получаем a=1/2, b=2/3, подставим эти значения в координаты вектора КМ: КМ { -1/3; 1/6; 1/6}. Найдём длину вектора |КМ| =√х²+y²+z², |КМ| =√1/9+1/36+1/36=√6/6. Ответ: √6/6
a·b = x1x2+y1y2+z1z2 = 0
Слайд 5
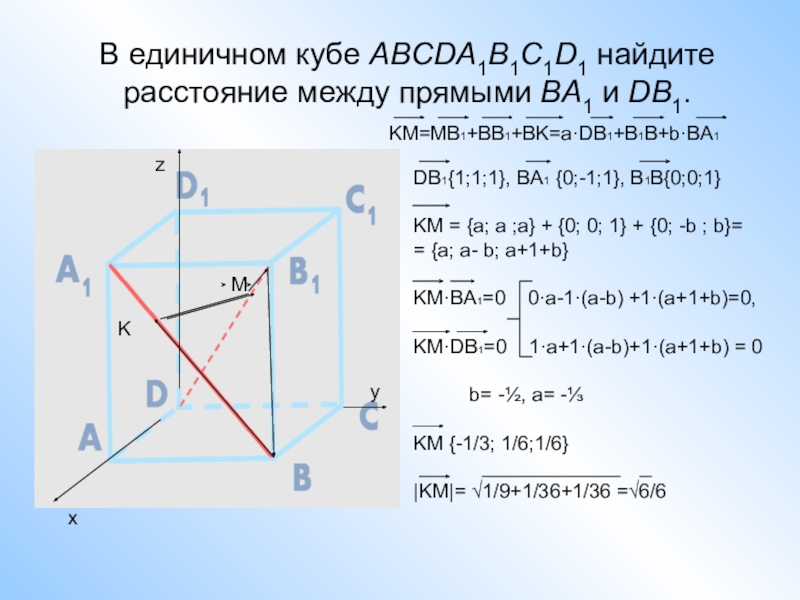
В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми BA1 и DB1.
K
M
x
y
z
KM=MB1+BB1+BK=a·DB1+B1B+b·BA1
DB1{1;1;1}, BA1 {0;-1;1}, B1B{0;0;1}
KM = {a;
= {a; a- b; a+1+b}
KM·BA1=0 0·a-1·(a-b) +1·(a+1+b)=0,
KM·DB1=0 1·a+1·(a-b)+1·(a+1+b) = 0
b= -½, a= -⅓
KM {-1/3; 1/6;1/6}
|KM|= √1/9+1/36+1/36 =√6/6
Слайд 6В правильной треугольной призме АВСА1В1С1, все ребра которой равны 1, найдите
z
y
x
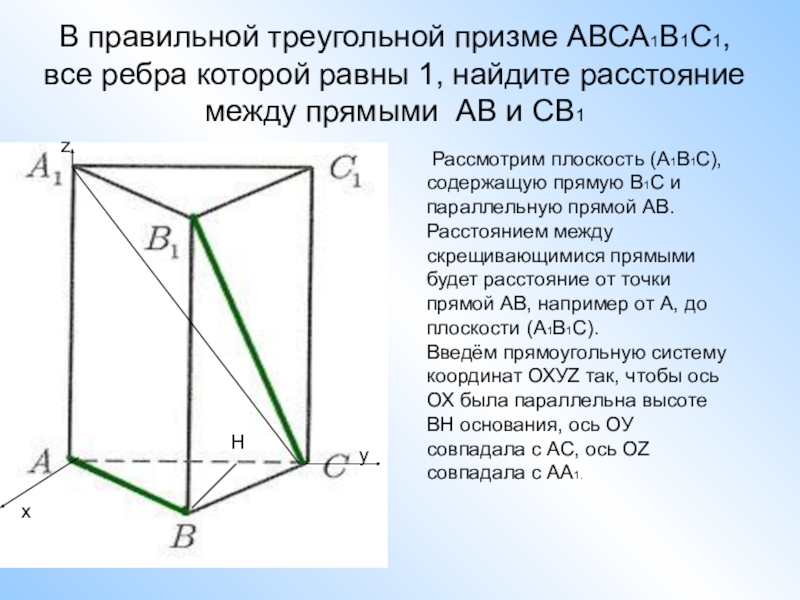
Рассмотрим плоскость (А1В1С), содержащую прямую В1С и параллельную прямой АВ. Расстоянием между скрещивающимися прямыми будет расстояние от точки прямой АВ, например от А, до плоскости (А1В1С).
Введём прямоугольную систему координат ОХУZ так, чтобы ось ОХ была параллельна высоте ВН основания, ось ОУ совпадала с АС, ось ОZ совпадала с АА1.
Н
Слайд 7Рассмотрим ∆АВС
в плоскости ОХУ
x
y
A
C
B
H
∆ ABC – правильный, АВ=ВС=АС=1, ВН=√3/2.
Составим уравнение
A1(0;0;1),
B1(√3/2; 1/2 ;1),
C(0;1;0) , подставляем координаты точек в уравнение плоскости, получим систему:
0A+0B+1C+D=0,
(√3/2)A+(1/2)B+1C+D=0,
0A+1B+0C+D=0.
Получаем C=-D, B=-D, A= (√3/3)D.
Уравнение плоскости (А1В1С1):
(√3/3)Dx-Dy-Dz+D=0, (√3/3)x-1y-1z+1=0,
Формула расстояния от точки до плоскости: d=
где (х0;у0;z0)- координаты точки A,
d = |√3/3·0-1·0-1·0 +1| / √ (√3/3)²+1+1 =√21/7. Ответ: √21/7.
х
у
z
H
Слайд 8 В правильной четырехугольной пирамидеSABCD, сторона основания 3√2, боковые ребра 5
M
K
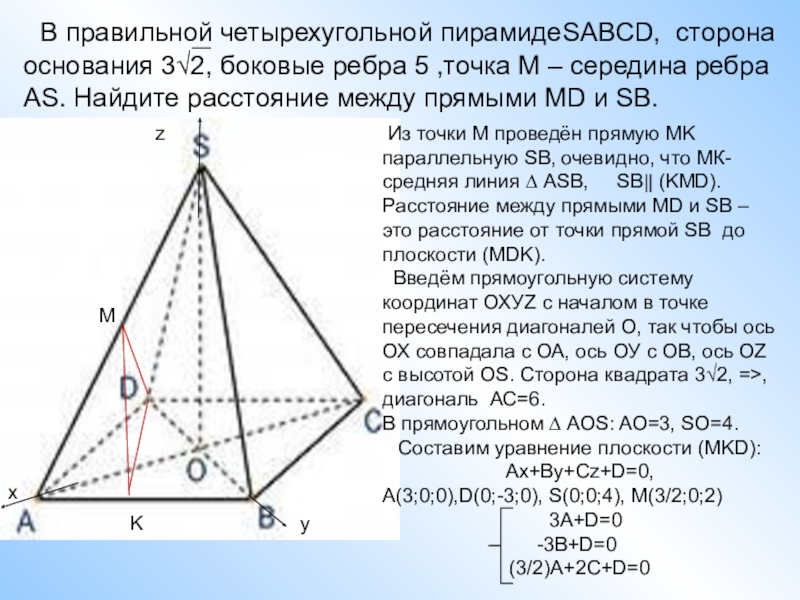
Из точки М проведён прямую MK параллельную SB, очевидно, что МК-средняя линия ∆ ASB, SB‖ (KMD). Расстояние между прямыми MD и SB – это расстояние от точки прямой SB до плоскости (MDK).
Введём прямоугольную систему координат ОХУZ с началом в точке пересечения диагоналей О, так чтобы ось ОХ совпадала с ОА, ось ОУ с ОВ, ось ОZ с высотой OS. Сторона квадрата 3√2, =>, диагональ АС=6.
В прямоугольном ∆ АОS: AO=3, SO=4.
Составим уравнение плоскости (MKD): Ax+By+Cz+D=0,
A(3;0;0),D(0;-3;0), S(0;0;4), M(3/2;0;2)
3A+D=0
3B+D=0
(3/2)A+2C+D=0
y
x
z
Слайд 9M
K
A= (- 1/3)D, B=(1/3)D, C=(-1/4)D.
Уравнение плоскости (МКD):
(-1/3)Dx+(1/3)Dy+(-1/4)Dz+D=0,
(-1/3)x+(1/3)y+(-1/4)z+1=0.
Определим расстояние от точки
d=|1+1|/√1/9+1/9+1/16=√41/12
Ответ: √41/12
z
x
y
Спасибо за внимание!!!