Искусство орнамента содержит в неявном виде наиболее древнюю часть известной нам высшей математики.
Г.Вейль
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Работа учеников. Описание монгольского орнамента математическими формулами.
Содержание
- 1. Работа учеников. Описание монгольского орнамента математическими формулами.
- 2. Перед вами самые
- 3. Когда на уроках математики мы изучали
- 4. И мы решили исследовать национальные орнаменты
- 5. Начнем с государственной эмблемы Соёмбо. Как
- 6. Графики в виде прямоугольников можно задавать
- 7.
- 8.
- 9.
- 10.
- 11.
- 12. Попробуем это релизовать :За основу выберем
- 13. Теперь, чтобы превратить квадрат в прямоугольник
- 14. |x-6y|+|x+6y|=6 |10x-2y|+|10x+2y| =10
- 15.
- 16. Для того чтобы нарисовать замысловатую кривую в центральном круге Соёмбо будем использовать функцию y=arcsin(x/k)
- 17.
- 18. Слайд 18
- 19. Запишем функции для окружностей, треугольников и полумесяца Соёмбо:
- 20. Окончательно имеем:
- 21. В монгольском орнаменте кроме прямоугольников мы
- 22. За основу возмем график уравнения :|x|+|y|=a
- 23. Добавив к |y-x| модуль |x| и
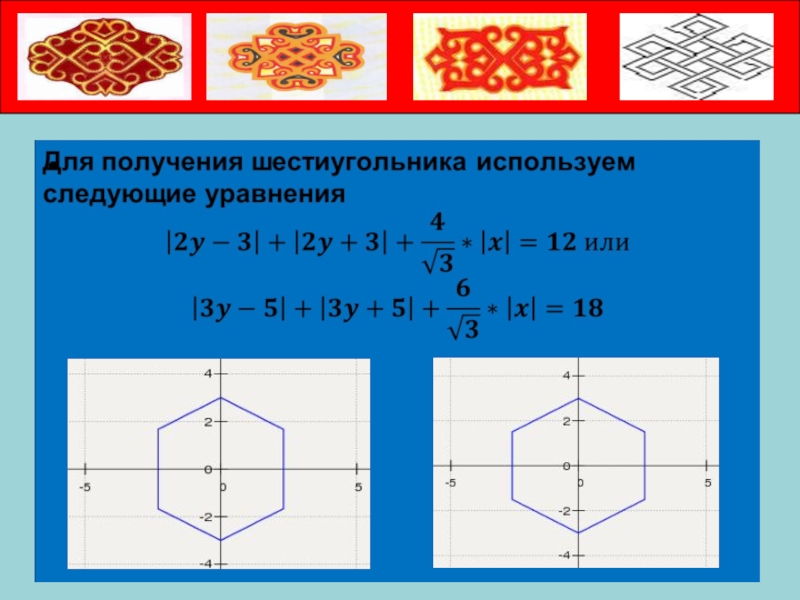
- 24. Шестиугольник : |x|+|y|+|y-x|=6Восьмиугольник : |x|+|y|+|x+y|+|y-x|=12 или другой восьмиугольник : |x|+|y|+|x+y|+|y-x|=18
- 25.
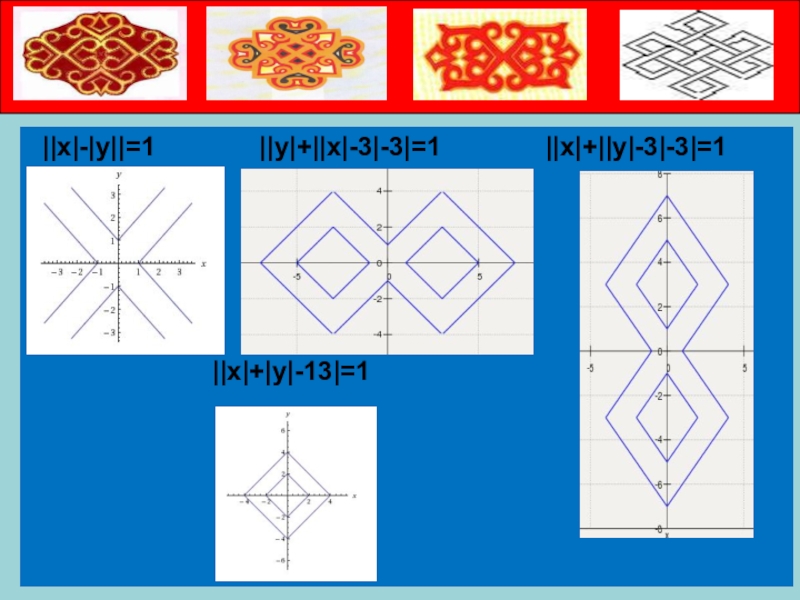
- 26. ||x|-|y||=1
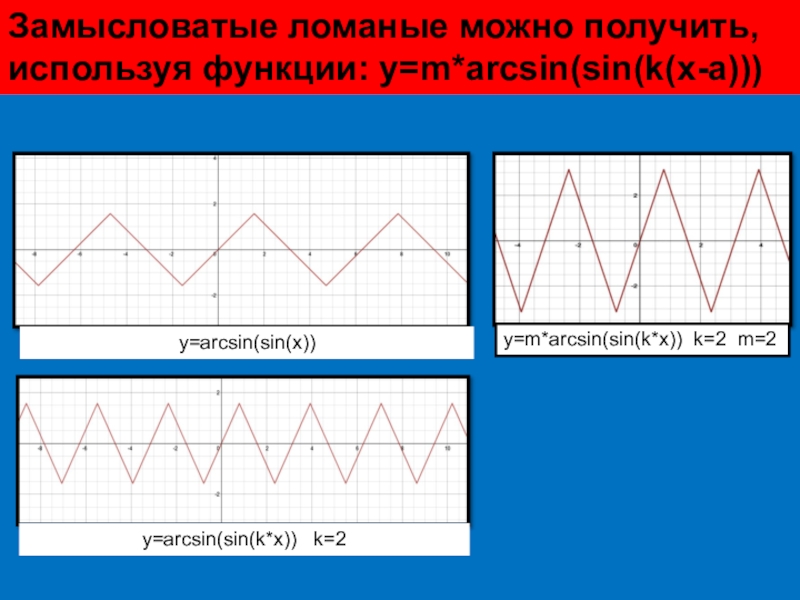
- 27. y=arcsin(sin(x))Замысловатые ломаные можно получить, используя функции: y=m*arcsin(sin(k(x-a)))y=arcsin(sin(k*x)) k=2y=m*arcsin(sin(k*x)) k=2 m=2
- 28. В заключении с помощью математических функций изобразим сердечки:
- 29. Авторы проекта:Ученики 11а класса: Агафонов Тэнгис и
- 30. Спасибо за внимание к нашей работе.
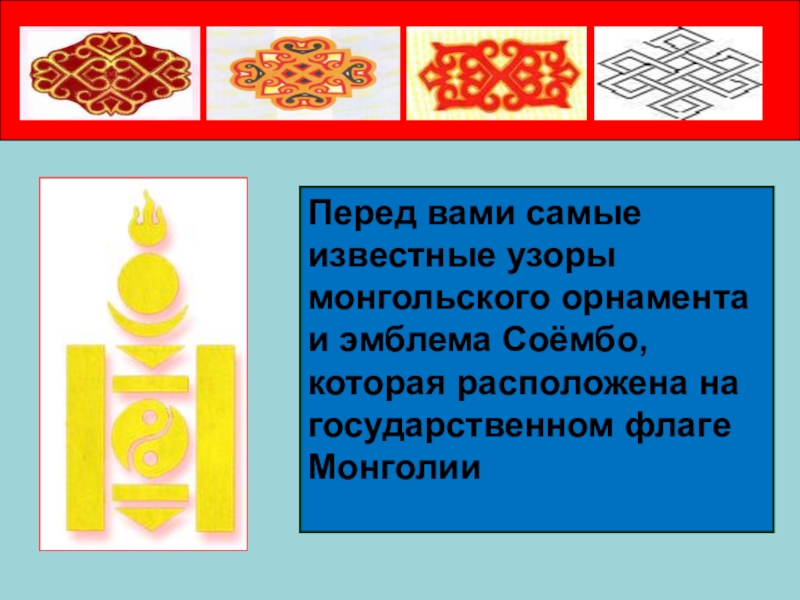
Перед вами самые известные узоры монгольского орнамента и эмблема Соёмбо, которая расположена на государственном флаге Монголии
Слайд 1
Школа при Посольстве России в Монголии.
Номинация “Хочу все знать”
Описание монгольского
орнамента математическими функциями
Слайд 2
Перед вами самые известные узоры монгольского
орнамента и эмблема Соёмбо, которая расположена на государственном флаге Монголии
Слайд 3
Когда на уроках математики мы изучали графики различных степенных, тригонометрических,
показательных и логарифмических функций, учителя показывали нам как влияет на вид графиков этих функций дополнительные параметры, модули, степени.
Слайд 4
И мы решили исследовать национальные орнаменты и описать их известными
математическими функциями.
И так, приступаем к исследованию. Для того, чтобы реализовать результаты наших исследований мы используем сайты: nigma.ru; desmos.com.
И так, приступаем к исследованию. Для того, чтобы реализовать результаты наших исследований мы используем сайты: nigma.ru; desmos.com.
Слайд 5Начнем с государственной эмблемы Соёмбо.
Как мы видим в этой
эмблеме четыре прямоугольника, два круга, полумесяц, два треугольника, полукруг – чаша с огнем, и замысловатая кривая, отделяющая инь и янь в центральном круге.
Слайд 6
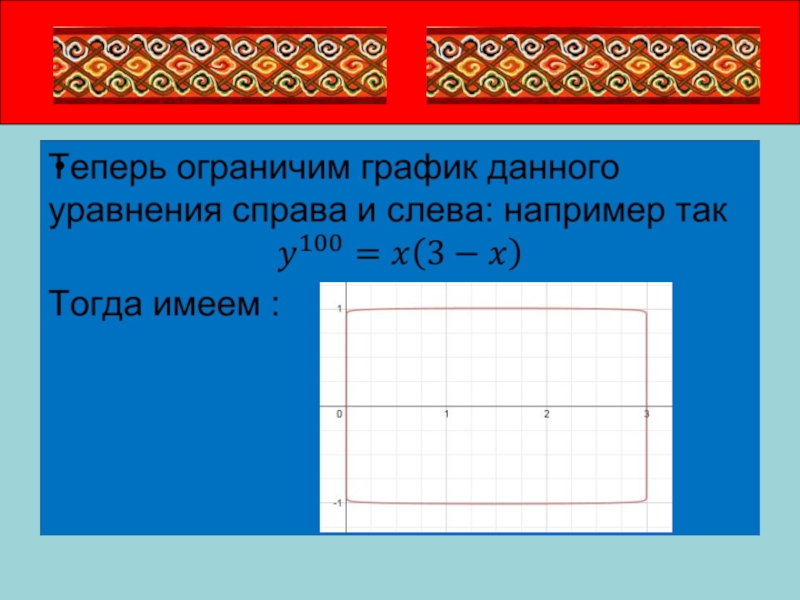
Графики в виде прямоугольников можно задавать двумя способами:
1. С помощью
степенных уравнений вида
y=x2k
2. С помощью уравнений, содержащих модули.
Реализуем каждый из этих способов.
y=x2k
2. С помощью уравнений, содержащих модули.
Реализуем каждый из этих способов.
Слайд 12
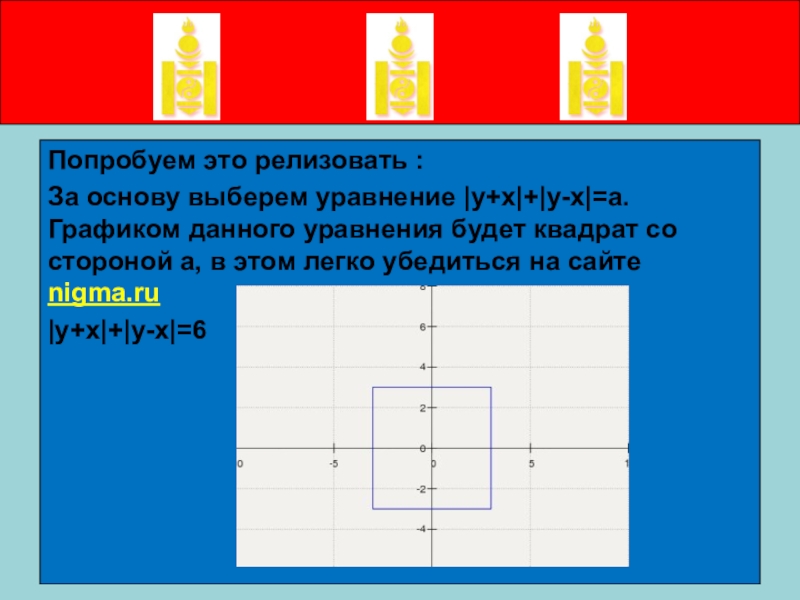
Попробуем это релизовать :
За основу выберем уравнение |y+x|+|y-x|=a. Графиком данного
уравнения будет квадрат со стороной a, в этом легко убедиться на сайте nigma.ru
|y+x|+|y-x|=6
|y+x|+|y-x|=6
Слайд 13
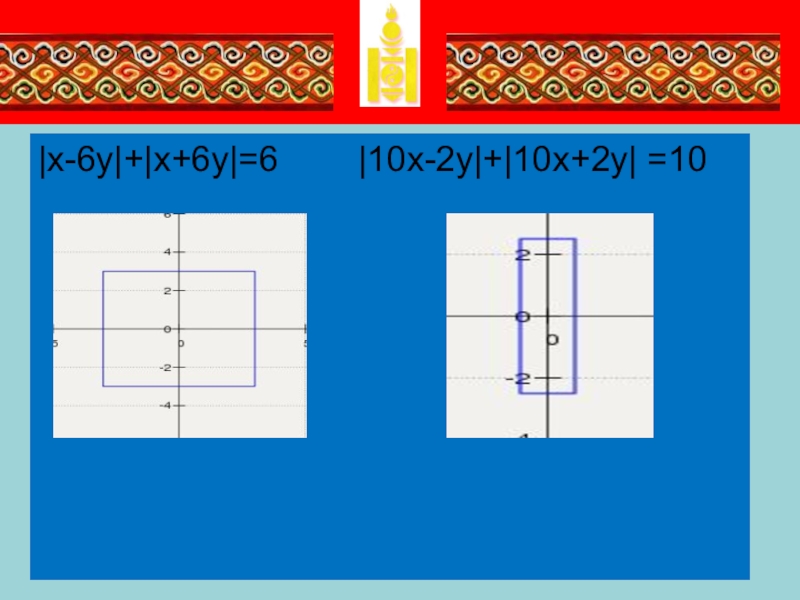
Теперь, чтобы превратить квадрат в прямоугольник достаточно ввести перед переменными
x и y коэффициенты. Тогда график уравнения: |kx+ly|+|ly-kx|=a есть прямоугольник со сторонами a/k и a/l Действительно на следующем слайде изображены графики уравнений :
|x-6y|+|x+6y|=6
|10x-2y|+|10x+2y| =10
|x-6y|+|x+6y|=6
|10x-2y|+|10x+2y| =10
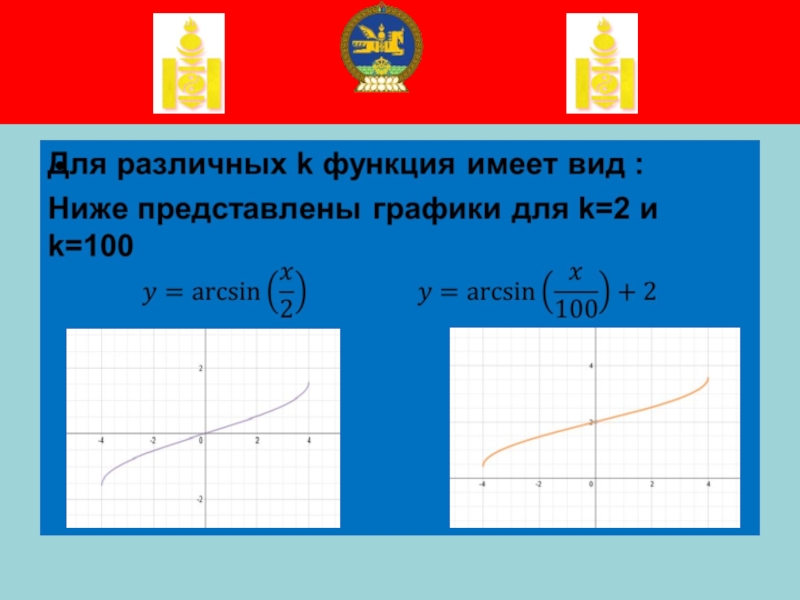
Слайд 16
Для того чтобы нарисовать замысловатую кривую в центральном круге Соёмбо
будем использовать функцию y=arcsin(x/k)
Слайд 21
В монгольском орнаменте кроме прямоугольников мы можем встретить ромбы, параллелограммы,
шестиугольники, восьмиугольники, более сложные фигуры. Попробуем реализовать их в виде графиков уравнений, содержащих модули.
Слайд 22
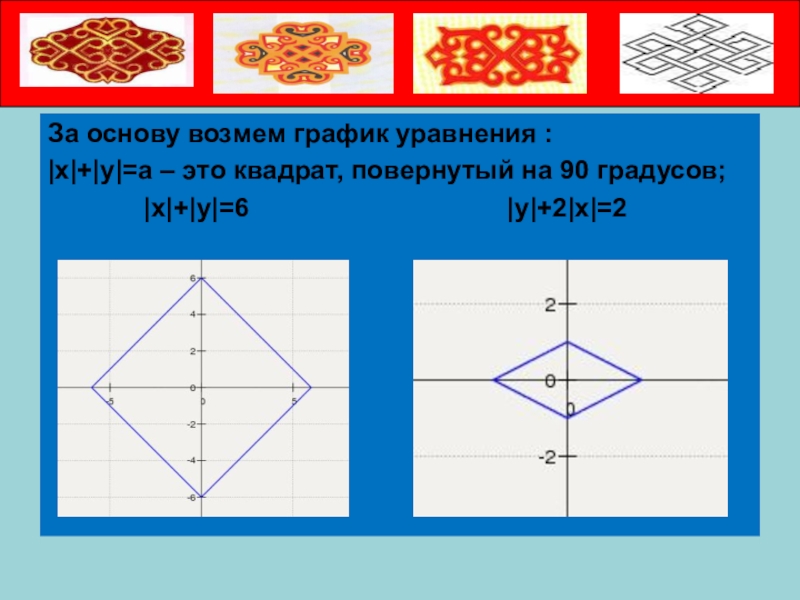
За основу возмем график уравнения :
|x|+|y|=a – это квадрат, повернутый
на 90 градусов;
|x|+|y|=6 |y|+2|x|=2
|x|+|y|=6 |y|+2|x|=2
Слайд 23
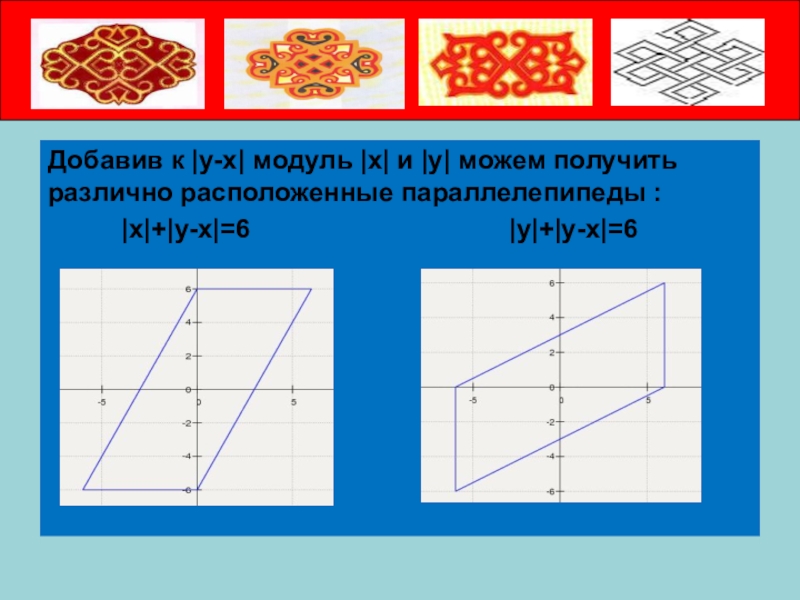
Добавив к |y-x| модуль |x| и |y| можем получить различно
расположенные параллелепипеды :
|x|+|y-x|=6 |y|+|y-x|=6
|x|+|y-x|=6 |y|+|y-x|=6
Слайд 24
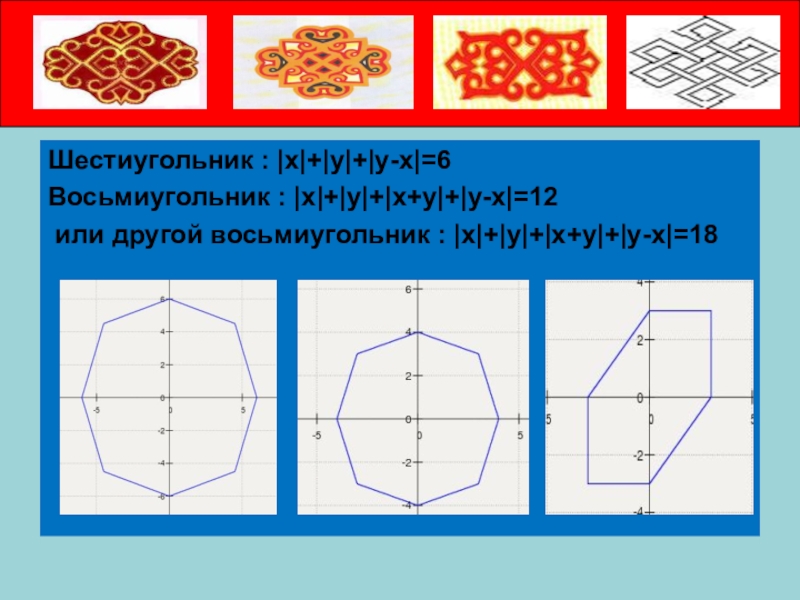
Шестиугольник : |x|+|y|+|y-x|=6
Восьмиугольник : |x|+|y|+|x+y|+|y-x|=12
или другой восьмиугольник : |x|+|y|+|x+y|+|y-x|=18
Слайд 27y=arcsin(sin(x))
Замысловатые ломаные можно получить, используя функции: y=m*arcsin(sin(k(x-a)))
y=arcsin(sin(k*x)) k=2
y=m*arcsin(sin(k*x)) k=2 m=2
Слайд 29Авторы проекта:
Ученики 11а класса:
Агафонов Тэнгис и Дэмбэрэлсурэн Нямхуу.
Ученики 10а класса:
Сэлэнгэ Онон и Жаргасайхан Суруулхунан.
Руководители. Учителя математики:
Дмитриев Сергей Степанович
Балашова Татьяна Николаевна